Предел функции на бесконечности с примерами решения

Подавляющее большинство функций, с которыми вы ознакомились ранее, определены на бесконечных промежутках. Исследуя такие функции, желательно установить их поведение для сколь угодно больших по модулю значений аргумента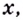 

Пусть функция 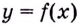 определена на интервале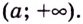 

 Число 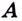 называется пределом функции  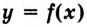на бесконечности  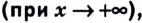если для любого  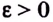существует такое число  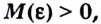что для всех  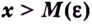выполняется неравенство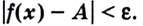 

Пишут: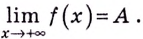 

Пусть функция 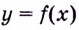 определена на интервале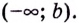 

 Число 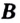 называется пределом функции  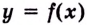на бесконечности  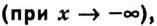если для любого  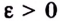существует такое число  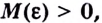что для всех  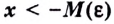выполняется неравенство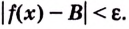 

Пишут: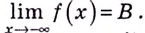 

Пусть функция 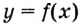 определена на интервале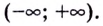 

 Число 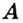 называется пределом функции  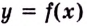на бесконечности  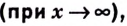если для любого  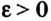существует такое число  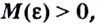что для всех  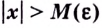выполняется неравенство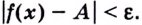 

Пишут: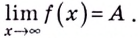 

Геометрически это означает, что для любого 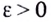 существует число  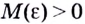такое, что для всех  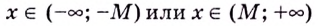соответствующие значения функции  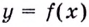попадают в  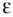-окрестность точки  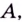то есть соответствующие точки графика этой функции лежат в полосе, ограниченной прямыми  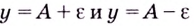(рис. 53).

Для предела функции на бесконечности выполняются те же свойства и теоремы о пределах, что и для предела функции в точке (см. с. 102), а также те правила, которые используются при вычислении предела числовой последовательности. А именно:

1 .Для того чтобы вычислить предел дробно-рациональной функции в случае, когда при 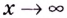 числитель и знаменатель дроби имеют пределы, которые равны бесконечности, необходимо сначала каждый член многочленов числителя и знаменателя дроби разделить на степень  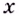с наибольшим показателем, а затем находить предел.

Пример:

Вычислите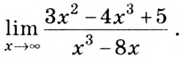 

Решение:

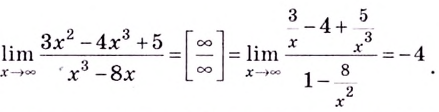
2. Для того чтобы вычислить предел функции, содержащей up рациональные выражения, в случае, когда каждый из слагаемых имеет бесконечный предел, необходимо умножить и разделить выражение, задающее функцию, на выражение, сопряжённое к нему, после этого выполнить необходимые упрощения (приведение подобных членов, сокращение и т. д.) и вычислить предел.

Пример:

Вычислите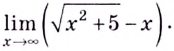 

Решение:

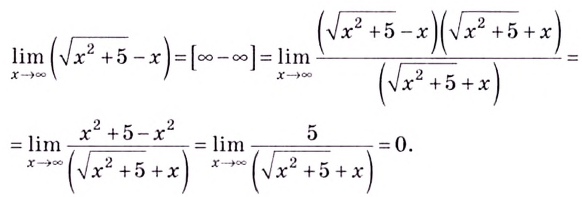
Исследуя функции, желательно также установить их поведение для тех значений аргумента 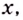 в которых функция бесконечно возрастает или убывает.

Функция 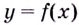 называется бесконечно большой при  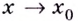(имеющей предел  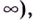 если для произвольного  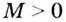существует такое число  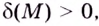что для всех  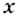таких, что  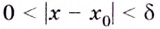выполняется неравенство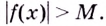 

Пишут: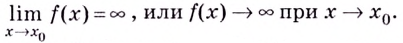 

Понятие предела функции на бесконечности и бесконечного предела используются для нахождения асимптот.

 Прямая 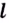 называется асимптотой кривой, если расстояние  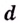от точки  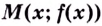кривой до этой прямой стремится к нулю при удалении точки  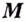в бесконечность.

Асимптотами, например, есть оси координат для графика функции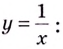 

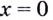 — вертикальная асимптота;

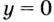 — горизонтальная асимптота.

Кривая 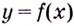 имеет горизонтальную асимптоту  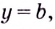если существует конечный предел функции  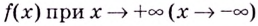и этот предел равен  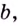то есть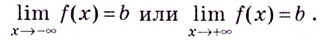 

• Заказать решение задач по высшей математике

Пример:

Найдите горизонтальную асимптоту кривой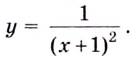 

Решение:

Вычислим предел 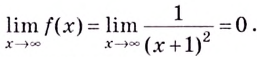 Следовательно,  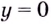- горизонтальная асимптота.

Пример:

Исследуйте поведение функци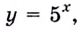и  если: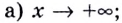 

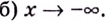
Решение:

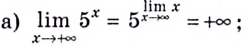
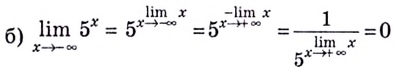
Пример:

Вычислите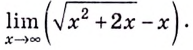 

Решение:

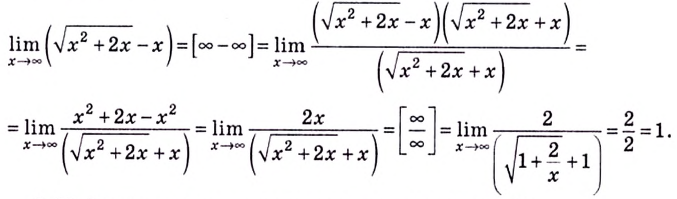
Пример:

Найдите горизонтальные асимптоты кривой:

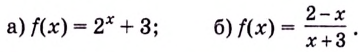
Решение:

а) Вычислим пределы при 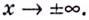 Имеем: 

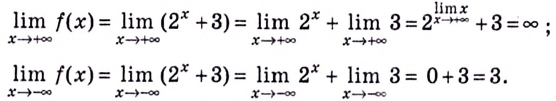
Следовательно, 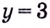 — горизонтальная асимптота д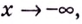ля  а для 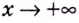 — асимптоты нет.

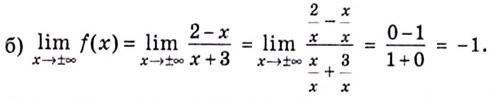
Следовательно, 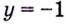 — горизонтальная асимптота.