Правило «трех сигм» в теории вероятности - определение и вычисление с примерами решения

Правило «трех сигм»:

Пусть случайная величина X имеет закон распределения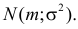

т.е. отклонения, большие 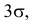имеют вероятность 0,003. Во многих приложениях такой вероятностью можно пренебречь и считать, что при единичном наблюдении нормально распределенной случайной величины интервалом практически возможных значений является интервал 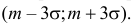Это утверждение обычно называют правилом «трех сигм». Заметим, что для любой случайной величины из неравенства Чебышева следует, что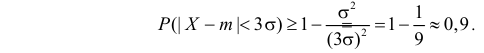

Поэтому правилом «трех сигм» иногда пользуются не печалясь о том, что случайная величина вовсе не имеет нормального закона распределения.

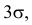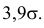Замечание. Последние годы все чаще предпочитают брать не а Тогда получается более «симпатичная» вероятность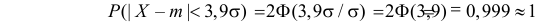

(Величина 0,999 впечатляет больше, нежели 0,997!)

Пример:

Монета подброшена 100 раз. Герб выпал 30 раз. Можно ли считать, что монета было симметричной?

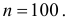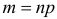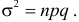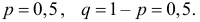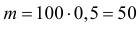Решение. Подбрасывание монеты можно считать независимым опытом, число которых Число появлений события в большой серии опытов имеет примерно нормальный закон распределения с параметрами и Если монета симметрична, то Тогда и 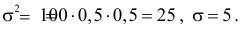Поэтому для симметричной монеты практически возможными значениями числа выпадений герба являются значения от 35 до 65. Число 30 к ним не принадлежит.

Ответ. При симметричной монете такой результат практически невозможен.

Пример:

Некто утверждает, что он экстрасенс. Для проверки был проделан следующий опыт. Взято пять карточек с рисунками простейших геометрических фигур. Испытатель выбирает карточку наугад, а испытуемый, находясь в соседней комнате, пытается определить, руководствуясь сверхчувственным восприятием, какая карточка выбрана экспериментатором. Карточки перемешиваются. Затем опыт повторяется. Так проделали 100 раз. Оказалось, что в 28 случаях испытуемый правильно назвал карточку. Есть ли основания считать, что имело место сверхчувственное восприятие?

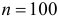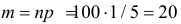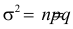
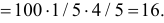Решение. Естественно предположить, что 28 совпадений произошли случайно. Вероятность угадать нужную карточку равна 1/5. Угадывание каждой карточки можно считать независимым опытом. Так как опытов много (), то число совпадений имеет близкий к нормальному закон распределения с параметрами и  Тогда 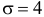и, согласно правилу «трех сигм», практически возможно угадать от 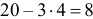до 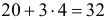раз. Число 28 входит в интервал возможных значений при простом угадывании. Следовательно, полученные опытные данные не подтверждают сверхчувственного восприятия.

Замечание. Предположим, что экстрасенс все-таки настаивает на своем сверхчуственном восприятии. Серию опытов повторили. Совпадений оказалось 31. В этом случае всего опытов 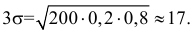Интервал практически возможных значений: (23;57). Общее число совпадений равно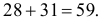

Такое число совпадений при простом угадывании практически невозможно. Это может послужить поводом для тщательной проверки условий эксперимента (подавляющее большинство так называемых экстрасенсов – откровенные жулики). Или следует настоять на лабораторном обследовании экстрасенса (от чего экстрасенсы всячески уклоняются, их стихия – работа на публику).