
Правило Лопиталя - определение и вычисление с примерами решения
Содержание:
Правило Лопиталя
Теорема 13.1 (правило Лопиталя). Пусть функции y=f(x) и y=g(x):
1) дифференцируемы в некоторой окрестности 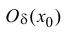
1. Если в п. 4 теоремы 13.1
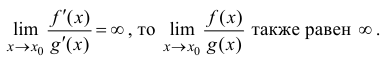
2. Аналогичная теорема верна и для односторонних пределов.
Теорема 13.2. Пусть M>0 и функции y=f(x) и y=g(x):
1) дифференцируемы при 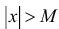 ;
;
2) 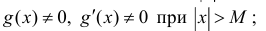
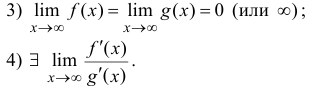
Тогда
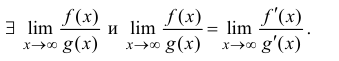
Доказательство
Пусть 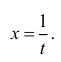 Рассмотрим функции
Рассмотрим функции 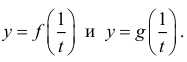
Тогда условия 1) –3) теоремы 13.1 выполнены в окрестности  .
.
Проверим условие 4):
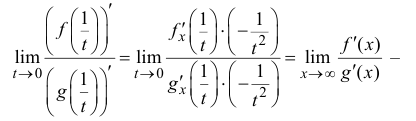
предел существует, поэтому по теореме 13.1
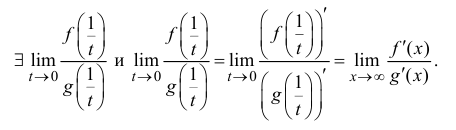
Тогда
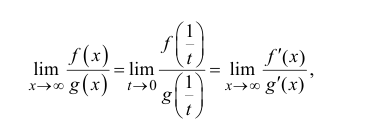
что и требовалось доказать.
По правилу Лопиталя раскрывают неопределенности типа 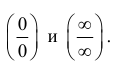 .
.
Неопределенности 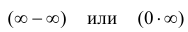 необходимо эквивалентными преобразованиями привести к виду
необходимо эквивалентными преобразованиями привести к виду 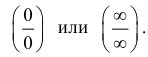 Неопределенности
Неопределенности 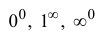 раскрывают путем предварительного логарифмирования.
раскрывают путем предварительного логарифмирования.
П р и м е р 13.1
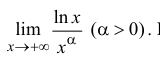
ПустьM>0. Функции 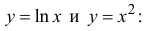
1) непрерывны и имеют производные при x> M;
2) 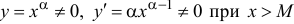 ;
;
3) 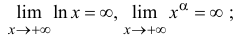
4)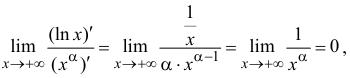 поэтому по теореме 13.2
поэтому по теореме 13.2
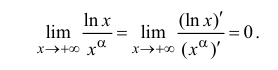
П р и м е р 13.2
Найти 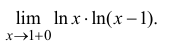
Р е ш е н и е
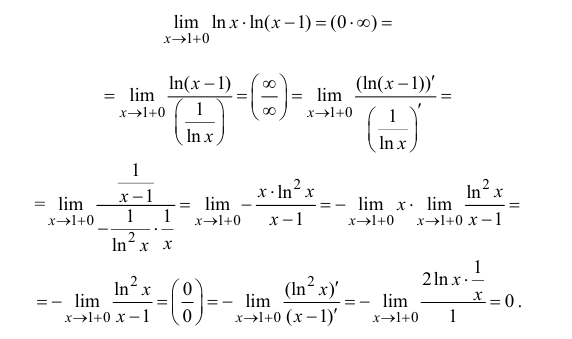
П р и м е р 13.3
Найти 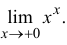
Р е ш е н и е
Имеем неопределенность вида 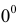 .
.
Преобразуем функцию 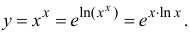
Найдем
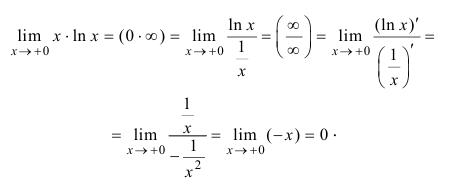
Поэтому
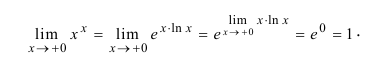
П р и м е р 13.4
Найти 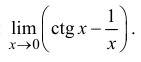
Р е ш е н и е
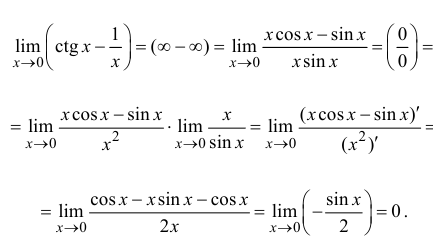
Если в условии теоремы 13.1 предположить дополнительно, что функции 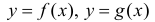 дифференцируемы в точке
дифференцируемы в точке 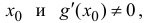 тогда формула (13.1) перепишется в виде
тогда формула (13.1) перепишется в виде
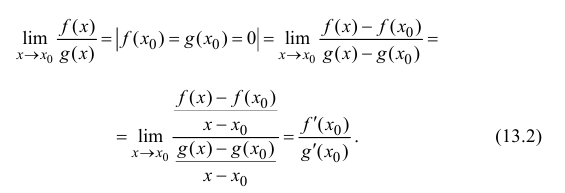
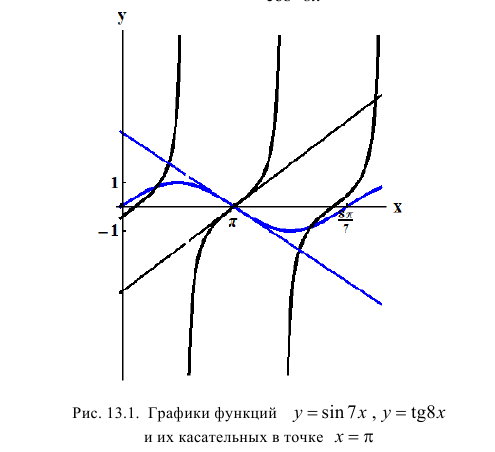
Геометрически это значит, что предел при 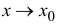 отношения значений функций
отношения значений функций 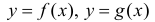 равен отношению угловых коэффициентов касательных к этим функциям в точке
равен отношению угловых коэффициентов касательных к этим функциям в точке 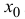 .
.
П р и м е р 13.5
Найти 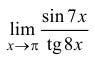 (см. пример 4.2).
(см. пример 4.2).
Р е ш е н и е
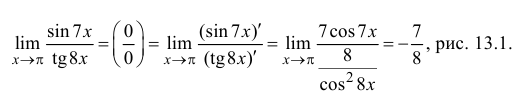
-------
Правило Лопиталя
Теорема 8.1. Пусть
1) функции 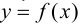 и
и 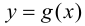 определены и непрерывны в проколотой окрестности
определены и непрерывны в проколотой окрестности 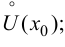
2) существуют конечные производные 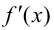 и
и 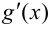 в
в 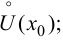
3) 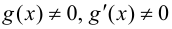 в
в 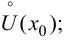
4) 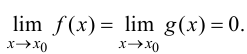
Тогда если существует 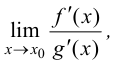 то существует
то существует 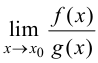 и имеет место равенство
и имеет место равенство
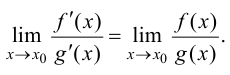
Доказательство.
Доопределим функции 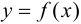 и
и 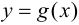 в точке
в точке 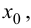 полагая
полагая
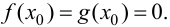
Тогда функции 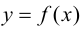 и
и 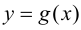 непрерывны в точке
непрерывны в точке 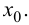 Используя теорему Коши (теорема 7.3), получим
Используя теорему Коши (теорема 7.3), получим
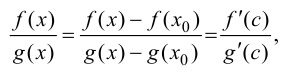
где точка 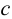 будет удовлетворять условиям
будет удовлетворять условиям 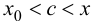 или
или 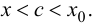 Если
Если 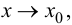 то
то 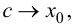 поэтому, согласно условию теоремы,
поэтому, согласно условию теоремы,
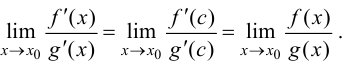
Теорема 8.1 формулирует правило раскрытия неопределенности типа 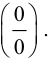
Замечание 8.1. Если производные 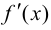 и
и 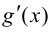 удовлетворяют тем же требованиям, что и сами функции
удовлетворяют тем же требованиям, что и сами функции 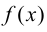 и
и 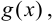 то правило Лопиталя можно применять повторно. При этом получаем
то правило Лопиталя можно применять повторно. При этом получаем
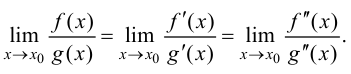
Пример 8.1. Найти предел 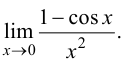
Решение.
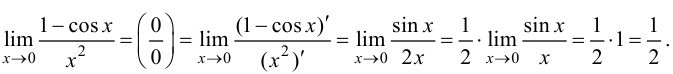
Ответ: 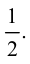
Пример 8.2. Найти предел 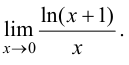
Решение.
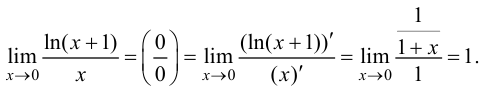
Ответ: 1
Пример 8.3. Найти предел 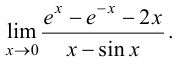
Решение.
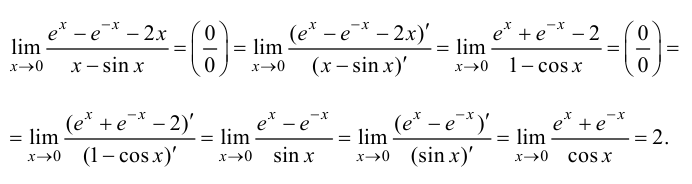
Ответ: 2.
Теорема 8.2*. Пусть
1) функции 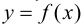 и
и 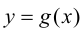 определены и непрерывны в проколотой окрестности
определены и непрерывны в проколотой окрестности 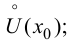
2) существуют конечные производные 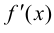 и
и 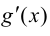 в
в 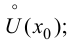
3) 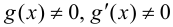 в
в 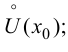
4) 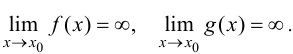
Тогда, если существует 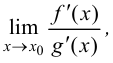 то существует
то существует 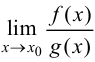
и имеет место равенство
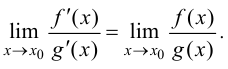
Теорема 8.2 формулирует правило раскрытия неопределенности
типа 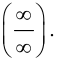
Замечание 8.2. Правило Лопиталя справедливо и в случаях 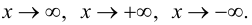
Пример 8.4. Найти предел 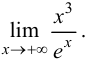
Решение.
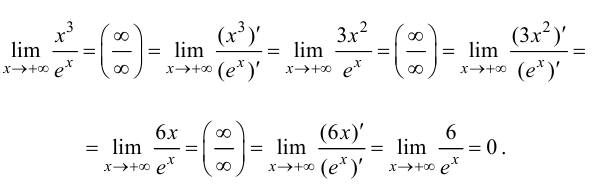
Ответ: 0.
Пример 8.5. Найти предел 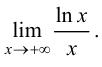
Решение.
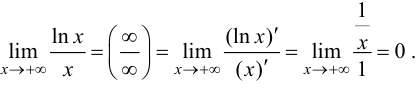
Ответ: 0.
Пример 8.6. Найти предел 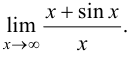
Решение.
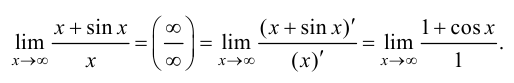
Полученный предел не существует, так как при 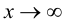 функция
функция 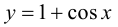 не стремится ни к какому предельному значению, а колеблется между 0 и 2. Правило Лопиталя не дает результатов. Рассмотрим другой подход к вычислению предела.
не стремится ни к какому предельному значению, а колеблется между 0 и 2. Правило Лопиталя не дает результатов. Рассмотрим другой подход к вычислению предела.
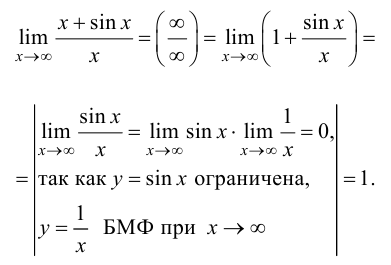
Ответ: 1.
Заметим, что правило Лопиталя дает также возможность раскрыть неопределенности типа 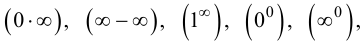 предварительно приведя их к виду
предварительно приведя их к виду 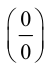 или
или 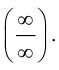
Пример 8.7. Найти предел 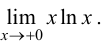
Решение.
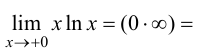
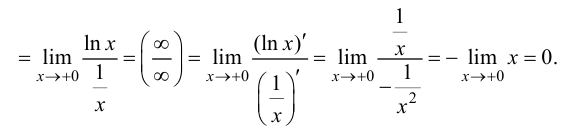
Ответ: 0.
Пример 8.8. Найти предел 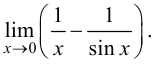
Решение.
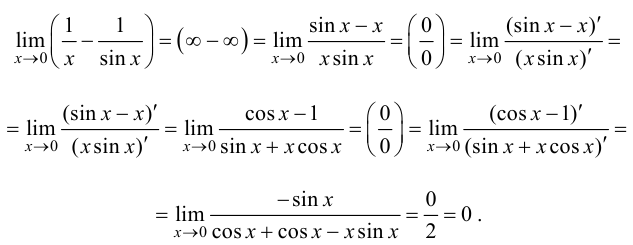
Ответ: 0.
Пример 8.9. Найти предел 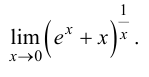
Решение.
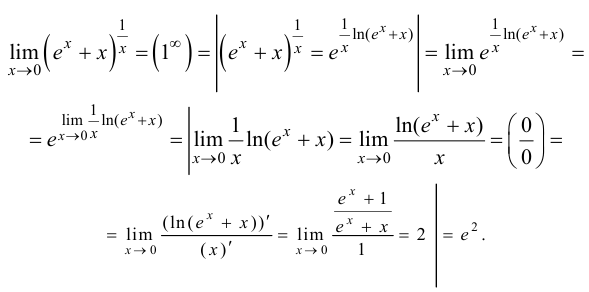
Ответ: 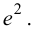
Пример 8.10. Найти предел 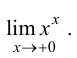
Решение.
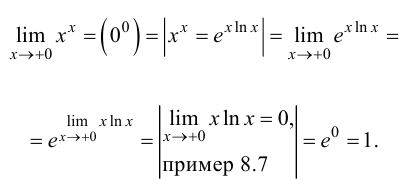
Ответ: 1.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |