Правильные многогранники в геометрии с примерами

Пусть есть плоский многоугольник

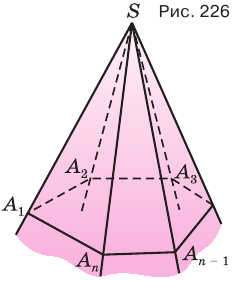
Многогранный угол называется выпуклым, если он расположен по одну сторону от плоскости любой его грани. Многогранный угол на рисунке 228 выпуклый, а на рисунке 229 — невыпуклый. По количеству граней многогранные углы разделяют на трехгранные, четырехгранные и т. д.

Теорема 12.

Сумма плоских углов выпуклого многогранного угла меньше 360°.

Доказательство:

Установим сначала, что каждый плоский угол трехгранного угла меньше суммы двух других его углов.

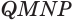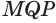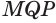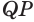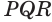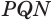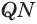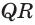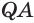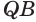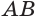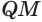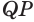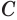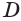Пусть есть трехгранный угол (рис. 230). Пусть для определенности угол — больший из плоских углов трехгранного угла. В плоскости грани от луча отложим угол , равный углу , и на лучах и отложим равные отрезки и . Через прямую проведем такую плоскость, которая пересекает ребра и в некоторых точках и . Треугольник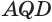и и 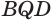равны, так как у них сторона 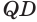общая, и по построению равны углы 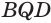и 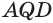, а также стороны 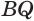и 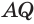. 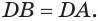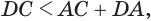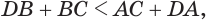Значит, Далее по свойству сторон треугольника получаем или или 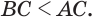Теперь, поскольку у треугольников 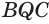и 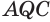сторона 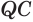общая, стороны 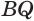и 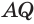равны, н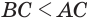о , то 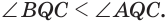Прибавив к левой и правой частям этого неравенства соответственно углы 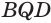и 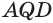, которые равны друг другу, получим, что 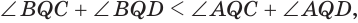или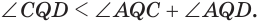

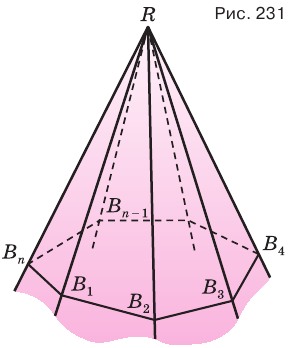
Пусть теперь есть выпуклый многогранный угол с вершиной 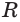(рис. 231). Если пересечь его какой-либо плоскостью, то в сечении получим многоугольник 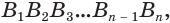каждая вершина которого является вершиной трехгранного угла, образованного двумя гранями данного угла и секущей плоскостью. По доказанному для этих трехгранных углов получаем:

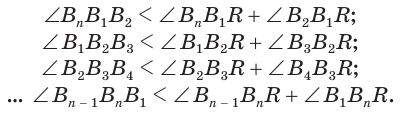
Сложим покомпонентно эти неравенства:

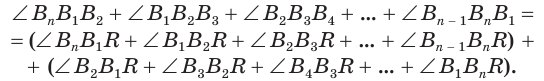
Теперь обратим внимание на то, что сумма в левой части последнего неравенства есть сумма углов многоугольника 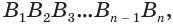которая равна 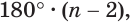а в правой — сумма углов всех треугольников 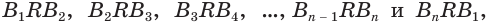но без их углов при вершине 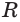, которая равна 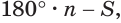где 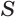выражает сумму плоских углов данного многогранного угла. Таким образом,

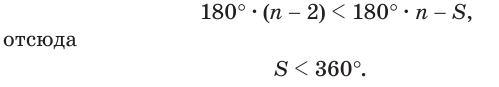
Многогранник, у которого все грани являются равными правильными многоугольниками и все двугранные углы равны друг другу, называется правильным многогранником.

Из этого определения следует, что у правильного многогранника равны друг другу все его:

• плоские углы;
• многогранные углы;
• ребра.

Теорема 13.

Количество ребер, сходящихся в каждой вершине правильного многогранника, не больше пяти.

Доказательство:

Допустим, что это не так, т. е. в вершине многогранника сходится шесть или больше ребер. Тогда при этой вершине многогранник имел бы шесть или больше равных плоских углов. Учитывая, что сумма этих углов меньше 360°, получаем, что каждый из них меньше 60°. Но это невозможно, поскольку гранями правильного многогранника являются правильные многоугольники, а у них углы не меньше 60°.

Теорема 14.

Количество сторон правильного многоугольника, являющегося гранью правильного многогранника, не больше пяти.

Доказательство:

В каждой вершине правильного многогранника сходится не менее трех плоских углов, а поэтому каждый из них должен быть меньше 120°. Вместе с этим угол правильного шестиугольника равен 120°, а угол правильного многоугольника с большим количеством сторон больше 120°. Поэтому правильные многоугольники, количество сторон которых больше пяти, не могут быть гранями правильного многоугольника.

Теорема 15.

Есть пять типов правильных многогранников.

Доказательство:

В соответствии с теоремой 14 гранями многогранника могут быть правильные треугольники, четырехугольники или пятиугольники.

Если гранями правильного многогранника служат треугольники, то, с учетом теоремы 13, в вершинах многогранника могут сходиться три, четыре или пять ребер. Если гранями правильного многогранника служат четырехугольники или пятиугольники, то в вершинах многогранника может сходиться только три ребра. Значит, существует не более пяти видов правильных многогранников.

Чтобы убедиться, что такие виды многогранников существуют, достаточно указать способ построения каждого из них.

Прежде всего отметим, что правильным многогранником, гранями которого служат правильные четырехугольники, т. е. квадраты, является куб, который еще называют правильным гексаэдром. Куб можно построить так. В произвольно выбранной плоскости построить квадрат, через его стороны провести плоскости, перпендикулярные выбранной плоскости, и провести еще одну плоскость, параллельную выбранной плоскости и отстоящую от нее на сторону квадрата (рис. 232). Мы видим, что гексаэдр имеет 6 граней, 12 ребер и 8 вершин.

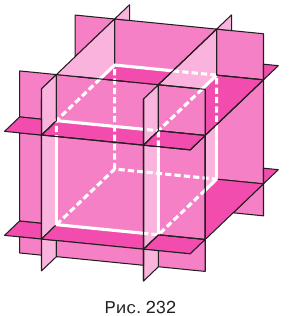
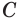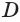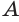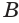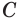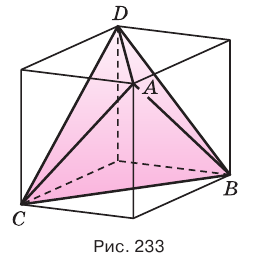
Построение многогранника, в каждой вершине которого сходится по три треугольные грани, может быть таким. Построить куб. Выбрать одну из его вершин и в каждой грани с этой вершиной выбрать вершину, противолежащую вершине . Пусть это вершины , , . Точки , , , 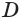являются вершинами искомого многогранника (рис. 233). Действительно, каждый из отрезков 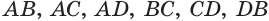является диагональю одной из граней куба, а поэтому все эти отрезки равны друг другу. Получается, что в треугольной пирамиде 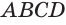все грани являются правильными треугольниками. Такая пирамида называется правильным тетраэдром. Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.

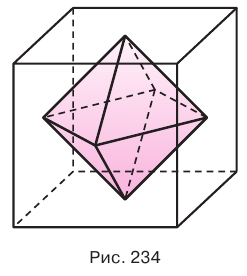
Построение многогранника, в каждой вершине которого сходится по четыре треугольные грани, может быть таким. Построить куб и найти центры шести его граней (рис. 234). Эти точки являются вершинами многогранника, все грани которого — правильные треугольники. Такой многогранник называется правильным октаэдром. Октаэдр имеет 8 граней, 12 ребер и 6 вершин.

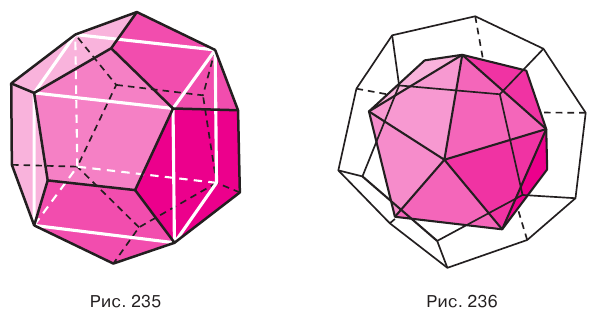
Построение многогранника, в каждой вершине которого сходится по три пятиугольные грани, можно выполнить, снова используя куб. Если через каждое из двенадцати ребер куба провести плоскость, которая не имеет с поверхностью куба других общих точек, кроме точек этого ребра, то полученные 12 плоскостей при пересечении дадут грани некоторого многогранника. Можно так подобрать наклон этих плоскостей к граням куба, что грани этого двенадцатигранника будут правильными пятиугольниками (рис. 235). Такой многогранник называется правильным додекаэдром. Додекаэдр имеет 12 граней, 30 ребер и 20 вершин.

Наконец, многогранник, в каждой вершине которого сходится по пять треугольных граней, можно построить, используя додекаэдр: центры граней додекаэдра являются вершинами искомого правильного многогранника (рис. 236). Такой многогранник называется правильным икосаэдром. Икосаэдр имеет 20 граней, 30 ребер и 12 вершин.

Таким образом, есть пять типов правильных многогранников.

Названия правильных многогранников происходят из греческого языка. Термин тетраэдр, по-гречески 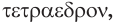означает четырехгранник: 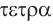— четыре и 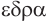— грань. Соответственно термины гексаэдр, октаэдр, додекаэдр, икосаэдр, по-гречески 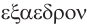, , 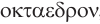, , 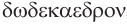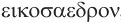означают шестигранник, восьмигранник, двенадцатигранник, двадцатигранник: 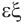, — шесть, 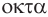— восемь, 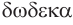— двенадцать, 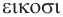— двадцать.

Мы знаем, что правильные гексаэдр и тетраэдр имеют описанный и вписанный шары. Также описанный и вписанный шары имеют октаэдр, додекаэдр и икосаэдр. Центры этих шаров совпадают, и эта точка является центром симметрии соответствующего правильного многогранника, кроме тетраэдра, который не имеет центра симметрии.