Поверхности вращения в начертательной геометрии с примерами

Содержание:

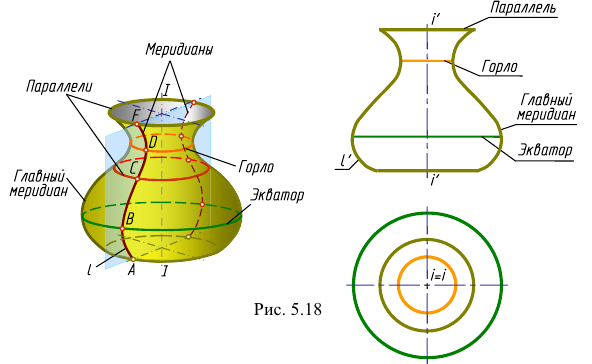
Поверхностей вращения существует множество: цилиндр, конус, сфера, эллипсоиды, торы и др. Поверхность вращения общего вида образуется вращательным перемещением образующей линии вокруг неподвижной оси. Каждая точка образующей линии при вращении вокруг неподвижной оси описывает окружность с центром на оси вращения. Эти окружности называются параллелями.

Наибольшую из параллелей (окружностей) поверхности вращения называют экватором поверхности, а наименьшую - горлом (шейкой) поверхности. Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, - меридианами. Меридиональная плоскость, параллельная плоскости проекции, называется плоскостью главного меридиана, а линия пересечения этой плоскости с поверхностью вращения называется главным меридианом.

Поверхности вращения

Поверхностью вращения называется поверхность, описываемая кривой (или прямой) образующей при ее вращении вокруг неподвижной оси (рис. 5.18). Эта поверхность определяется на чертеже заданием образующей и оси вращения.

Каждая точка образующей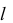

Плоскость, проходящую через ось поверхности вращения, называют меридиональной. Линию ее пересечения с поверхностью - меридианом. Меридиан, параллельный фронтальной плоскости проекций, называется главным меридианом. Все меридианы равны между собой.

На чертеже ось вращения 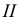располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.

Точки на поверхностях вращения могут быть построены с помощью параллелей, то есть окружностей на поверхности (рис. 5.20, рис. 5.22, а, б, в, рис. 5.23 - рис. 5.25).

Рассмотрим некоторые тела и поверхности вращения.

1 .Поверхности, образованные вращением прямой линии:

а) цилиндр вращения - поверхность, полученная вращением прямой 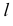вокруг параллельной ей оси 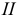(рис. 5.19);

б) конус вращения - поверхность, образованная вращением прямой 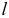вокруг пересекающейся с ней осью 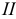(рис. 5.20);

в) однополостный гиперболоид вращения - поверхность, полу­ченная вращением прямой 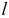вокруг скрещивающейся с ней осью 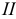(рис. 5.21).

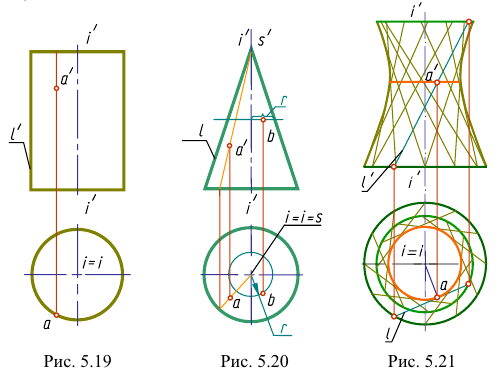
Точка А, лежащая на перпендикуляре к оси вращения и обра­зующей, будет описывать наименьшую окружность, являющуюся горлом гиперболоида. Однополостный гиперболоид может быть также получен вращением гиперболы вокруг ее мнимой оси.

2. Поверхности, образованные вращением окружности вокруг неподвижной оси: а) сфера - поверхность, полученная вращением окружности во­круг ее диаметра (рис. 5. 22, а);

б) тор - поверхность, полученная вращением окружности вокруг оси 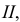лежащей в плоскости этой окружности, но не проходящей через ее центр (рис. 5.22, б-д).

Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор - кольцо» (рис. 5.22, б); если ось касается окружности, то образованная поверхность называются «закрытый тор» (рис. 5.22, в); если ось пересекает окружность - «самопересекающийся тор» (рис. 5.22, г, д)). Тор, изображенный на рис. 5.22, г, назы­вается также «тор-яблоко», а на рис. 5.22, д — «тор-лимон». Сфера - частный случай торовой поверхности.

3. Поверхности вращения, образованные вращением кривых вто­рого порядка:

а) эллипсоид вращения - поверхность, полученная вращением эллипса вокруг оси (рис. 5.23). Поверхность, образованная вращением эллипса вокруг его большой оси, называется вытянутым эллипсоидом вращения (рис. 5.23, б), при вращении вокруг малой оси - сжатым элипсоидом вращения (рис. 5.23, а, в);

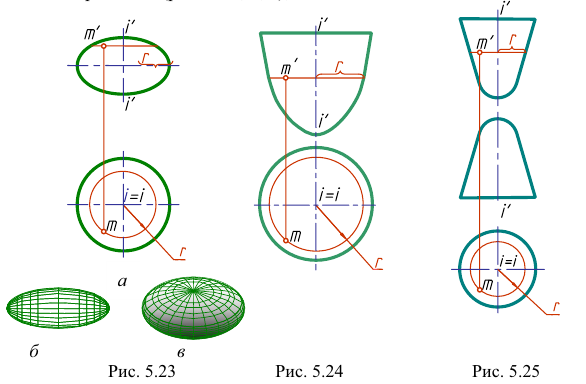
б) параболоид вращения - поверхность, образованная вращением параболы вокруг ее оси (рис. 5.24);

в) двухполостный гиперболоид вращения - поверхность, обра­зованная вращением гиперболы вокруг ее действительной оси (рис. 5.25).

Пересечение поверхностей вращения плоскостью

При пересечении поверхности вращения плоскостью получается линия сечения - плоская фигура. Построение проекций линии пересечения необходимо начинать с определения опорных точек. К ним относятся точки, расположенные на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой), и точки, удаленные на экстремальные (максимальное и минимальное) расстояния от плоскостей проекций. После этого определяют произвольные (промежуточные) точки линии пересечения.

Для определения точек, принадлежащих линии пересечения, можно использовать различные методы. Один из них - метод вспомогательных секущих плоскостей. Суть его заключается в том, что заданные плоскость и поверхность вращения пересекают вспомогательными плоскостями. Находят линии пересечения этой плоскости с заданными плоскостью и поверхностью вращения. Затем отмечают точки, в которых пересекаются полученные линии пересечения. Построенные точки фигуры сечения соединяют плавной кривой линией.

Развертки поверхностей вращения

Построение разверток поверхностей вращения имеет большое значение, особенно при конструировании из листового материала моделей различных сооружений, форм для металлических отливок, сосудов, трубопроводов, резервуаров и т.п.

Приближенные развертки

Поверхности, которые можно совместить с плоскостью без разрывов и складок, называют развертывающимися поверхностями. Фигуру, полученную при совмещении развертывающейся поверхности с плоскостью, называют разверткой. Для развертывающихся поверхностей можно построить приближенную развертку (условно-развертываемые поверхности). При построении приближенной развертки поверхность аппроксимируют поверхностями вписанных или описанных многогранников, имеющих грани в форме прямоугольников или треугольников. Поэтому при графическом выполнении разверток поверхности всегда приходится производить разгибание или спрямление кривых линий, принадлежащих поверхности, что неизбежно приводит к потере точности.

Условные развертки

Неразвертывающиеся поверхности не могут быть совмещены сплоскостью без разрывов и складок, т.е. теоретически они не имеют своей развертки. Поэтому говорят лишь об условном решении задачи по построению разверток неразвертывающихся поверхностей. На практике для получения развертки неразвертываемой поверхности, выполненной из листового материала, приходится кроме изгибания производить растяжение и сжатие определенных участков листа.

Построение условной развертки неразвертывающейся поверхности состоит в том, что отсеки заданной поверхности аппроксимируются отсеками развертывающихся поверхностей — гранными, цилиндрическими или коническими.  

Задание: построить проекции и натуральный вид фигуры сечения поверхности цилиндра плоскостью Р (рис. 11.1). Построить развёртку боковой поверхности усечённой части цилиндра.  

Решение: на рисунке 11.1 изображены прямой круговой цилиндр, основание которого принадлежит горизонтальной плоскости проекций 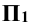и секущая плоскость Р общего положения. Поскольку секущая плоскость наклонена к оси цилиндра, то боковая поверхность цилиндра пересекается по эллиптической кривой.Форма сечения в этом случае зависит от того, пересекает ли плоскость Р основания цилиндра. В рассматриваемом случае секущая плоскость Р не пересекает оснований цилиндра. Это видно из того, что горизонтальная проекция нижнего основания не пересекается с горизонтальным следом плоскости Р, а горизонтальная проекция горизонтали 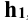, по которой плоскость Р пересекается с плоскостью верхнего основания, не пересекает его горизонтальную проекцию.

Для нахождения эллипса сечения плоскости Р с боковой поверхностью цилиндра находят сначала его низшую 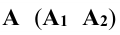и высшую 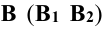точки.

Эти точки являются концами большой оси эллипса сечения и лежат на линии наибольшего наклона плоскости Р к горизонтальной плоскости проекций. Следовательно, прямая АВ перпендикулярна к горизонтальному следу плоскости Р и пересекает ось цилиндра.

Для нахождения точек А и В проводят плоскость Σ, перпендикулярную к горизонтальному следу 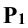и проходящую через ось цилиндра. Эта плоскость перпендикулярна к плоскости 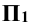. Затем находят линию пересечения плоскостей Р и Σ.

Боковая поверхность цилиндра является горизонтально проецирующей и поэтому проецируется на горизонтальную плоскость проекций в окружность. Так как отрезок АВ является частью линии пересечения плоскостей Р и Σ, а точки А и В лежат на боковой поверхности цилиндра, то горизонтальные проекции точек А и В должны лежать на одной окружности и на горизонтальной проекции прямой пересечения плоскостей Р и Σ. По горизонтальным проекциям точек А и В находят их фронтальные проекции, исходя из условия, что точки А и В лежат на найденной прямой пересечения плоскостей Р и Σ.

Для определения остальных точек эллипса сечения на цилиндрической поверхности выбирают ряд образующих. За первую образующую выбирают ту, на которой лежит точка А. Остальные образующие получают делением окружности (горизонтальной плоскости цилиндрической поверхности) на 12 равных частей (можно делить на другое количество частей). Затем находят точки пересечения образующих с плоскостью Р. В рассматриваемом примере все образующие перпендикулярны к горизонтальной плоскости проекций. Следовательно, горизонтальные проекции точек пересечения образующих с плоскостью Р совпадают с горизонтальными проекциями самих образующих.

Далее наносят горизонтальные проекции точек пересечения образующих с плоскостью Р (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) и находят фронтальные проекции этих точек, проводя через них горизонтали в плоскости.

Кривая линия, ограничивающая фронтальную проекцию фигуры сечения, включает видимые и невидимые участки. Точки, являющиеся границей видимости кривой, лежат на очерковых образующих. Отмечают горизонтальные проекции этих точек (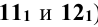) и находят фронтальные проекции (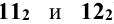), проводя через эти точки в плоскости Р горизонтали. Полученные точки соединяют плавной кривой линией. Кривая от точки 12 через точки 10, А, 1, 2, 3, 4 до точки 11 на фронтальной плоскости проекций является видимой, а остальная часть - невидимой.

Видимую часть кривой обводят сплошной линией, а невидимую - штриховой. Малой осью эллипса сечения является отрезок 3 - 8, проецирующийся в натуральную величину на горизонтальную плоскость проекций. Натуральная величина малой оси эллипса в рассматриваемом примере равна диаметру цилиндра. Натуральную величину эллипса сечения строят путём совмещения плоскости Р с горизонтальной плоскостью проекций.

Развёртка боковой поверхности прямого кругового цилиндра, не усечённого плоскостью, представляет собой прямоугольник с основанием, равным длине окружности основания цилиндра, и высотой, равной высоте цилиндра. При построении развёртки боковой поверхности цилиндра, пересечённого плоскостью, на развёртке необходимо наносить точки, принадлежащие линии пересечения, и затем эти точки соединять плавной кривой линией (рис. 11.1).

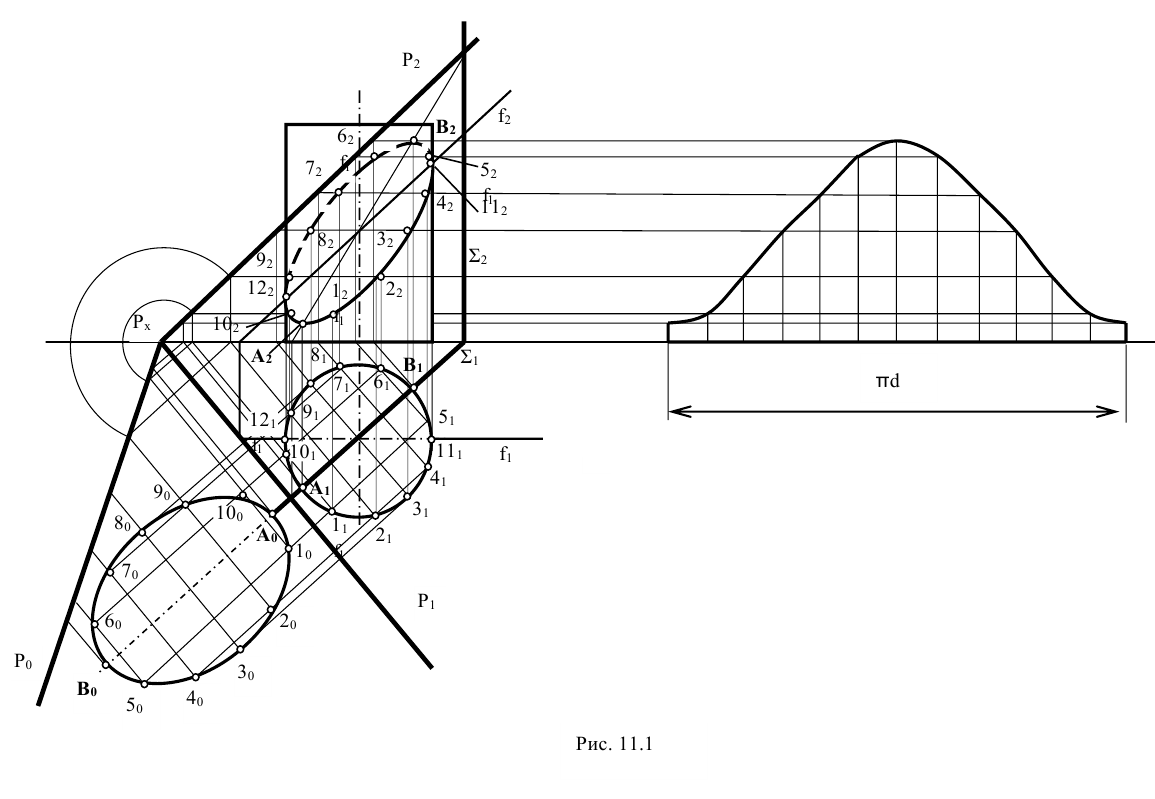
Для этого на развёртке боковой поверхности цилиндра проводят 12 образующих, отстоящих друг от друга на равном расстоянии. За первую образующую рекомендуется выбирать ту, на которой лежит точка А. Затем наносят на все образующие последовательно точки А, 1, 2, 3, 4, 11, 5, В, 6, 7, 8, 9, 12, 10. Расстояние от этих точек до нижнего (или верхнего) основания проецируется на фронтальную плоскость проекций в натуральную величину. Соединив полученные точки плавной кривой линией, получают развёртку боковой поверхности усечённой части цилиндра.  

• Заказать чертежи

Задание: построить проекции и натуральную величину линии пересечения поверхности конуса плоскостью Р (рис. 11.3).  

Решение: поверхность прямого кругового конуса относится к поверхностям вращения и является носителем кривых второго порядка: окружности, эллипса, параболы и гиперболы. Все эти кривые являются плоскими и, следовательно, могут быть получены в результате сечения конической поверхности плоскостью.

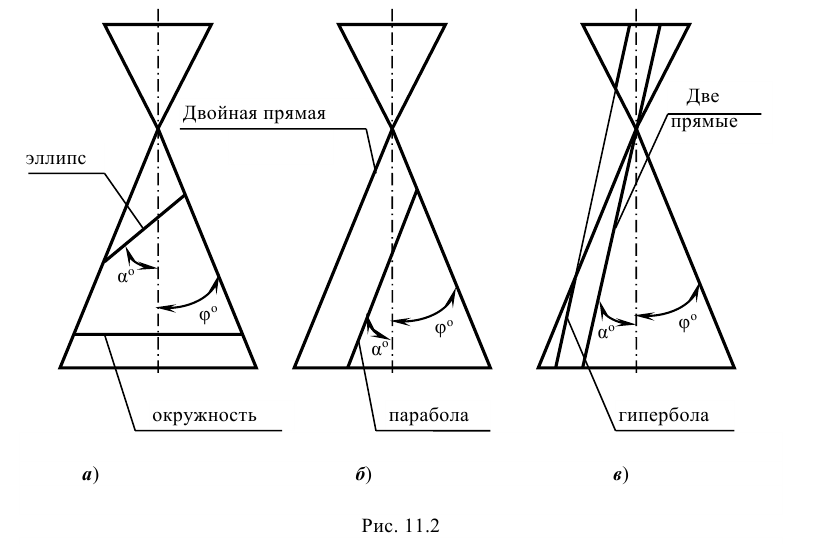
На рис. 11.2 приведены фронтальные проекции поверхности прямого кругового конуса, следы фронтально проецирующих секущих плоскостей и указан вид получаемой в сечении кривой. Можно установить признаки, обеспечивающие получение в сечении той или иной кривой второго порядка. Так, если обозначить угол наклона образующей конической поверхности к его оси через φ а угол между секущей плоскостью и той же осью через α , то можно утверждать, что при α > φ (рис. 11.2, а) в сечении получается эллипс (в частном случае, если α =90° - окружность), при α = φ (рис. 11.2, б) - парабола, и при α < φ (рис. 11.2, в) - гипербола.

На рис. 11.3 изображен прямой круговой конус и пересекающая его фронтально проецирующая плоскость Р. Угол между секущей плоскостью и осью конической поверхности больше угла наклона образующей конической поверхности к его оси, поэтому в сечении получается эллипс, большая ось которого АВ будет проецироваться на плоскость - 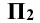без искажения в 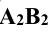, а малая ось эллипса 1-2 спроецируется на плоскость П 2 в точку 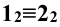, расположенную в середине отрезка 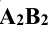. Величина малой оси 1-2 определяется из условия принадлежности ее плоскости Р. Для построения горизонтальной проекции малой оси 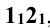применяют способ секущих плоскостей. Поверхность конуса рассекают горизонтальной вспомогательной секущей плоскостью 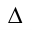и строят на горизонтальной проекции конуса проекцию фигуры сечения — круг.

Определяют горизонтальные проекции малой оси эллипса 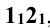, которые лежат на линии пересечения (окружности) плоскости А и поверхности конуса, и проводят ряд вспомогательных секущих плоскостей для нахождения промежуточных точек 3, 4, 5, 6, принадлежащих фигуре сечения (эллипсу). Натуральную величину эллипса находят совмещением плоскости Р с горизонтальной плоскостью проекции. Эллипс  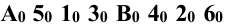есть натуральная величина эллипса.  

Задание: построить проекции и натуральную величину сечения конуса плоскостью Р (рис. 11.4). Построить развёртку усечённой части боковой поверхности конуса.  

Решение: на рис. 11.4 изображены прямой круговой конус и секущая плоскость Р общего положения. Ось конуса расположена перпендикулярно к плоскости 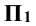основание конуса лежит на плоскости .

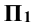Решение задачи значительно упростится, если секущая плоскость Р будет проецирующей. Для этого преобразуют чертеж методом перемены плоскостей проекций, чтобы секущая плоскость Р стала фронтально проецирующей.

Построенная на  проекция показывает, что секущая плоскость пересекает только боковую поверхность конуса, не затрагивая его основания.

Для нахождения проекций сечения необходимо найти проекции эллипса, получаемого от пересечения конической поверхности плоскостью. На фронтальную плоскость проекции эллипс проецируется в виде отрезка 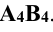. Точки А и В являются низшей и высшей точками эллипса (линии пересечения плоскости поверхностью конуса, т. е. концами большой оси эллипса). 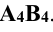— натуральная величина большой оси эллипса. Малая ось эллипса перпендикулярна к большой оси и делит её пополам. 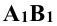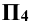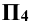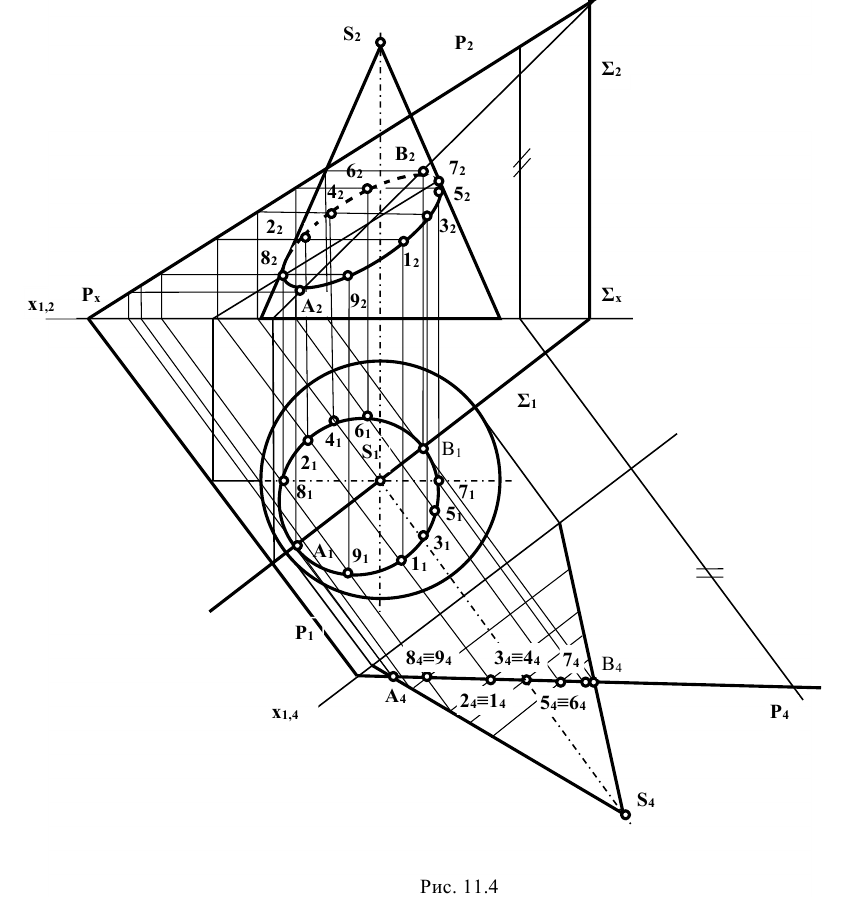Большая ось эллипса параллельна плоскости проекций , а малая ось перпендикулярна и проецируется на неё в точку .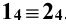

Затем задают на эллипсе сечения ещё ряд точек (3, 4, 5, 6, 7, 8). По их фронтальным проекциям на плоскость 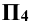находят горизонтальные проекции (проводя через точки на конической поверхности образующие). По горизонтальным проекциям находят фронтальные проекции на плоскость проекций 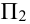(проводя фронтали через проекции точек).

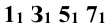Для нахождения границы видимости кривой на фронтальной проекции находят проекции очерковых образующих, на которых лежат искомые точки, на фронтальную плоскость проекций 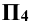. На пересечении этих образующих с плоскостью Р и будут искомые точки (проекции 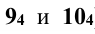). По проекциям 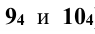находят горизонтальные проекции 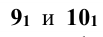а затем фронтальные проекции 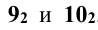. Видимая часть кривой на фронтальной проекции - от точки 10 через точки А, 5, 1, 3, 7 до точки 9. Остальная часть невидимая. Развёртка боковой поверхности прямого кругового конуса представляет собой сектор круга, радиус которого равен образующей конуса (рис. 11.5). Центральный угол сектора подсчитывается по формуле  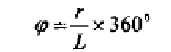где φ - радиус окружности основания конуса; L - длина образующей конуса.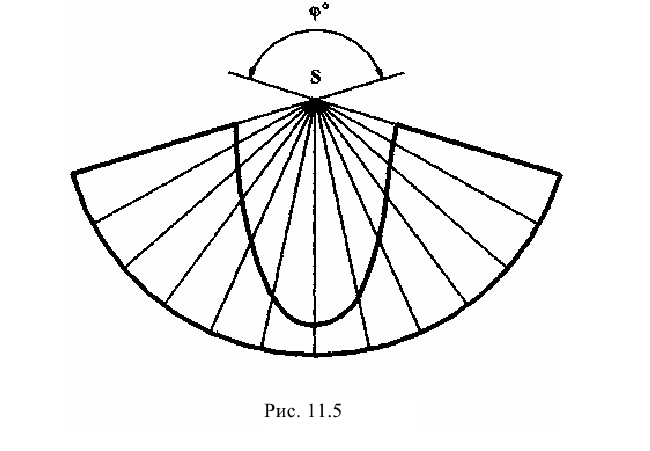

Чтобы избежать вычислений, связанных с определением длины дуги сектора или угла φ, обычно вписывают в основание конуса правильный многоугольник (в данном случае 12-угольник) и затем, описывают из произвольной точки S дугу радиусом L, откладывают последовательно из любой её точки количество дуг, равное сторонам многоугольника. Таким образом, развёртку боковой поверхности прямого кругового конуса заменяют, с достаточной для практики точностью развёрткой правильной пирамиды, вписанной в данный конус. Для нанесения на развёртку боковой поверхности конуса линии сечения (рис. 11.5) переносят на развёртку точки пересечения с секущей плоскостью 12 образующих конуса, которые заменены рёбрами 12- угольной правильной пирамиды. Соединив полученные точки плавной кривой, получают развёртку усечённой части боковой поверхности конуса.  

Задание: построить проекции линии пересечения сферы плоскостью Р (рис. 11.6).

 

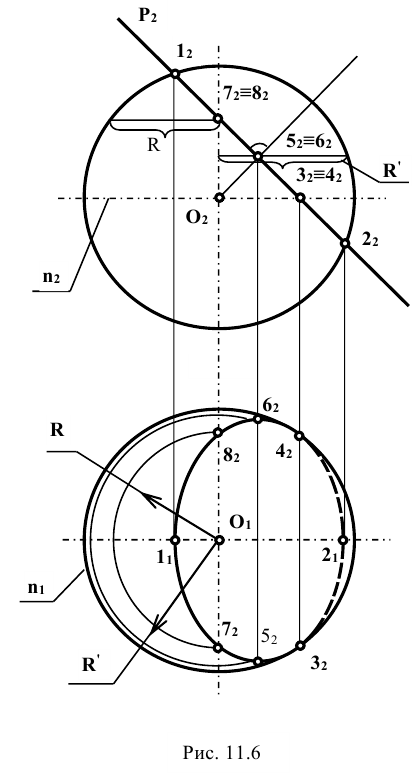
Решение: плоскость Р является фронтально проецирующей. На фронтальную плоскость проекций окружность (фигура сечения) проецируется в виде отрезка прямой, на горизонтальную - в виде эллипса. Эллипс строят по точкам. Точки 1 и 2 расположены на главном меридиане сферы, а точки 3 и 4 - на экваторе сферы. Для нахождения верхней и нижней (экстремальных) точек 5 и 6 определяют их фронтальные проекции 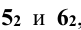, которые находятся в середине фронтальной проекции отрезка 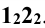. Через фронтальные проекции точек проводят фронтальную проекцию окружности 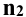(на плоскость 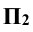она проецируется в прямую линию). Расстояние от оси сферы до очерковой образующей определяет радиус окружности R'. Этим радиусом строят горизонтальную проекцию окружности 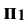и на ней находят проекции точек 5 и 6 - 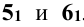. Промежуточные точки 7 и 8 определяют аналогичным способом.  

Задание: построить проекции и истинную величину линии пересечения сферы плоскостью общего положения 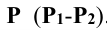 (рис. 11.7).  

Решение: для решения задачи плоскость общего положения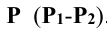 преобразуют методом замены плоскостей проекций в проецирующую.

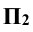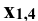Заменяют фронтальную плоскость проекции на Проводят ось перпендикулярно к горизонтальному следу 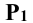плоскости Р. Строят плоскость Р в новой системе плоскостей /.

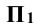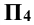Для этого берут на фронтальном следе 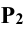плоскости Р произвольную точку 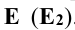Находят горизонтальную проекцию 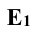точки Е, затем строят проекцию 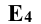в системе 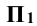/ 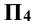. Через проекцию 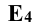и точку схода следов на оси x проводят фронтальный след плоскости 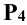. Проекцию сферы переносят в систему /.

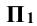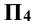Для этого проводят через горизонтальную проекцию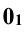, центра 0 сферы линию проекционных связей перпендикулярно к оси 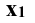и отмечают на ней (на линии проекционных связей) координату z точки 0. Полученную проекцию обозначают 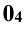. Затем строят проекцию сферы заданного радиуса в системе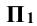 . После преобразования плоскости Р в проецирующее положение задача сводится к решению предыдущей задачи (см. п. 11.2.6), т. е. сначала строят горизонтальную проекцию фигуры сечения, а затем, используя признак принадлежности точки плоскости, строят фронтальную проекцию фигуры сечения сферы плоскостью общего положения.

Для определения натуральной величины сечения сферы необходимо выполнить вторую замену (плоскость проекций 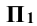 заменить на плоскость  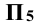(рис. 11.7). С этой целью преобразовывают плоскость сечения Р в плоскость уровня. Проводят ось 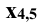параллельно фронтальному следу 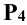. Проецируют центр окружности 0 в систему /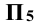. Рис. 11.7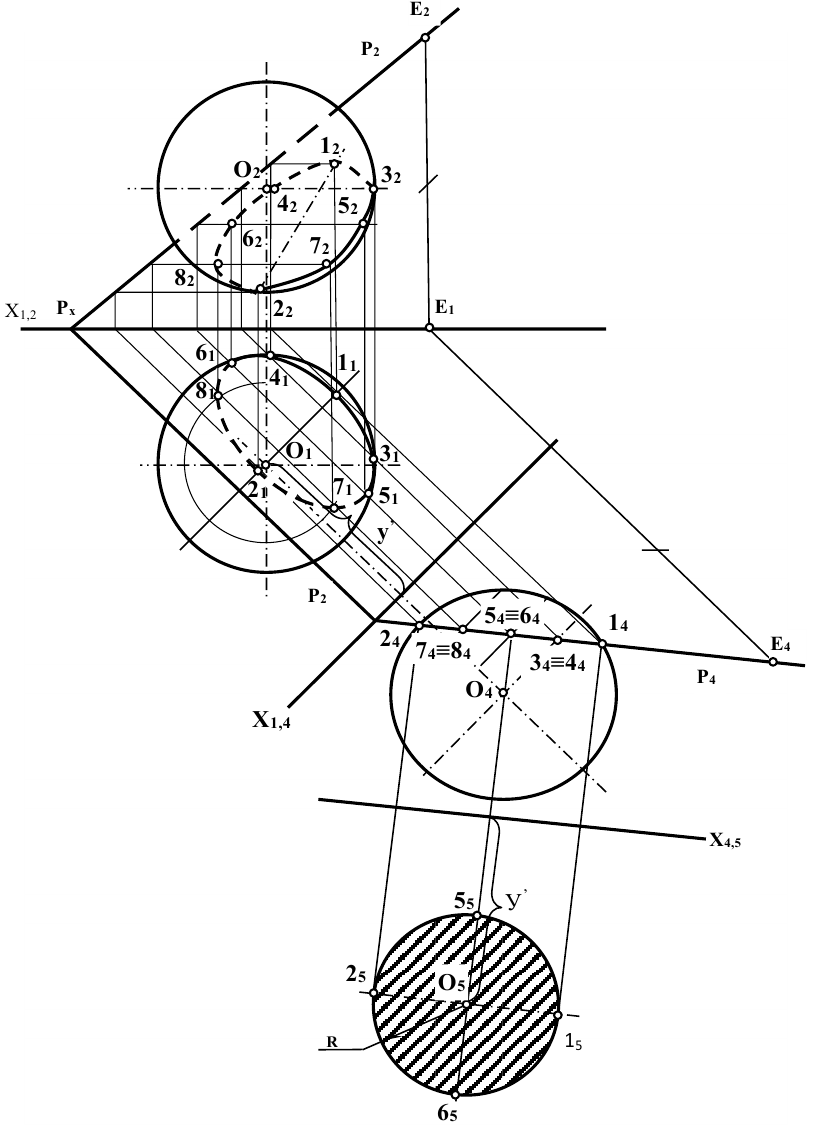

Натуральная величина сечения окружности строится радиусом R, равным половине отрезка .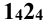

Поверхность сферы не может быть развёрнута точно. Для неразвертываемых поверхностей строят приближённую развёртку (рис. 11.8). Поверхность сферы разбивается на равное число частей (рис. 11.8, а), например, на 12 частей. Разбивку производят плоскостями, проходящими через один из диаметров сферы MN.

Каждую часть поверхности сферы, находящуюся между двумя смежными плоскостями, заменяют частью цилиндрической поверхности с осью, проходящей через центр сферы и перпендикулярной к диаметру MN. Диаметр поверхности принимают равным диаметру сферы.

Для наглядности ниже рассмотрено построение только одной из частей поверхности сферы, расположенной между плоскостями Р и Σ . Выделенную часть поверхности сферы заменяют цилиндрической с осью 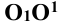, которая перпендикулярна к диаметру MN и плоскости дуги 1-4. Дугу 1-4 делят на равные части (в каждом случае - на три). Для построения развёртки откладывают на вертикальной прямой отрезки, равные хордам данных дуг 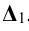. Величины этих хорд с достаточной степенью точности можно считать равными величинам дуг. По горизонтальной прямой откладывают величины соответствующих образующих поверхности 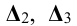и т.д. Полученные точки соединяют кривой линией (рис. 11.8, б).