
Потенциальное силовое поле в теоретической механике
Содержание:
Потенциальное силовое поле:
Для вычисления работы силы на каком-либо перемещении в общем случае необходимо знать закон движения точки на этом перемещении. Есть класс сил, для которых работа не зависит от характера движения точки на рассматриваемом перемещении. Эти силы называют потенциальными, и они имеют важное значение в различных областях механики и физики.
Потенциальное силовое поле и силовая функция
Силовым полем называют часть пространства, в каждой точке которого на материальную точку действует определенная сила, зависящая от координат точки и времени. Силовое поле считают стационарным, если действующие силы не зависят от времени. Если же силы зависят от времени, то силовое поле является нестационарным.
Силовое поле называют потенциальным, если имеется силовая функция 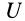
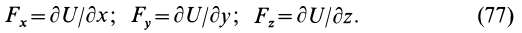
Функцию 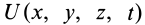 называют силовой функцией.
называют силовой функцией.
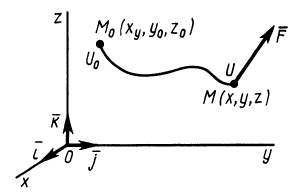
Рис. 72
Рассмотрим основные свойства силовой функции стационарного силового поля. Из (77) следует, что силовая функция определяется с точностью до постоянной, так как для проекций силы на координатные оси требуются только частные производные по координатам от этой функции и добавление постоянной к функции 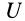 не влияет на значения
не влияет на значения 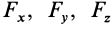 . Элементарная работа
. Элементарная работа
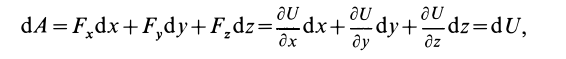
т. e.

Таким образом, элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции. Иногда это свойство силовой функции принимают за ее определение; тогда (77) получают из (78).
Полная работа силы 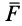 на участке от точки
на участке от точки 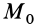 до точки
до точки 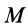
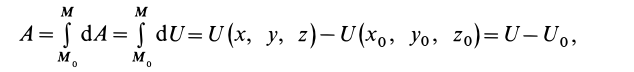
т.е.

где 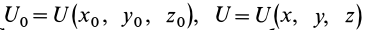
Следовательно, полная работа силы на каком-либо перемещении точки равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой оно совершается, если силовая функция является однозначной.
Из (79) следует, что работа силы в потенциальном силовом поле по любому замкнутому пути равна нулю, так как значение силовой функции в начальной и конечной точках перемещения одинаково, если силовая функция не принимает других значений после возвращения в первоначальную точку.
Силовая функция может принимать другие значения после возвращения в первоначальную точку в зависимости от количества обходов, если область, ограниченная замкнутым путем обхода, содержит в себе специальные особые точки силовой функции.
Если применить понятие вектор-градиента от скалярной функции 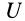
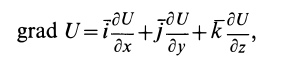
где 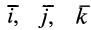 — единичные векторы, направленные по осям координат, то силу
— единичные векторы, направленные по осям координат, то силу 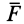 можно выразить как градиент силовой функции
можно выразить как градиент силовой функции 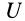 :
: 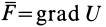
Определим условия, которые позволяют по силам силового поля устанавливать, будет ли силовое поле потенциальным.
Если силовая функция 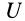 существует, то
существует, то
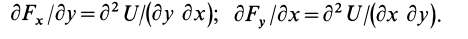
Так как
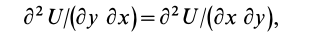
то
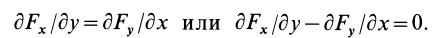
Аналогично,
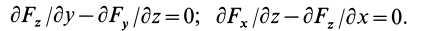
Таким образом, полученные условия имеют вид
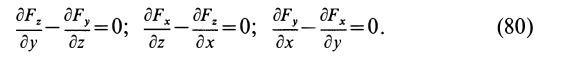
В векторном исчислении доказывается, что условия (80) не только необходимы, но и достаточны для существования силовой функции. Если использовать вектор вихря 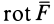 от вектора силы
от вектора силы 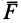
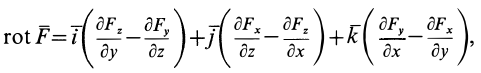
то условия (80) можно выразить более кратко:

Таким образом, для того чтобы силовое поле было потенциальным, необходимо и достаточно, чтобы оно было безвихревым.
Непотенциальными силами являются силы сопротивления, зависящие от скорости, и силы трения. Силы сухого трения не будут потенциальными, так как хотя сила трения постоянна и не зависит от скорости, но направление силы трения от скорости зависит.
Поверхности уровня и силовые линии
Если рассматривать точки потенциального силового поля, в которых силовая функция имеет одно и то же значение, например 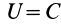 , то все эти точки располагаются на поверхности, которую называют поверхностью равного уровня или поверхностью уровня.
, то все эти точки располагаются на поверхности, которую называют поверхностью равного уровня или поверхностью уровня.
Уравнение поверхности уровня имеет вид
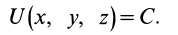
Отметим некоторые свойства поверхностей уровня.
1. Работа силы равна нулю, если начальная и конечная точки перемещения лежат на одной поверхности уровня. Действительно,
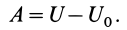
Если начальная и конечная точки лежат на одной поверхности уровня, то 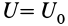 и, следовательно,
и, следовательно, 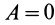 . Работа силы на перемещении между точками
. Работа силы на перемещении между точками 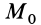 и
и 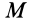 не зависит от положения этих точек на своих поверхностях уровня. На любом перемещении между двумя точками рассматриваемых поверхностей уровня она одинакова (рис. 73).
не зависит от положения этих точек на своих поверхностях уровня. На любом перемещении между двумя точками рассматриваемых поверхностей уровня она одинакова (рис. 73).
2. Сила в потенциальном силовом поле всегда перпендикулярна поверхности уровня или, точнее, касательной плоскости поверхности уровня. Действительно, пусть имеем поверхность уровня 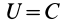 . Возьмем на ней две бесконечно близкие точки
. Возьмем на ней две бесконечно близкие точки 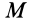 и
и 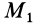 и вычислим элементарную работу на перемещении
и вычислим элементарную работу на перемещении 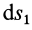 между этими точками:
между этими точками:
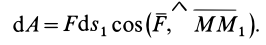
С другой стороны,
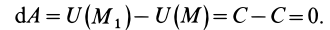
Так как 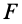 и
и 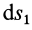 не равны нулю, то
не равны нулю, то 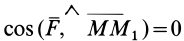 и, следовательно, угол между силой
и, следовательно, угол между силой 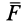 и перемещением
и перемещением 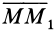 , лежащим в касательной плоскости к поверхности уровня, является прямым.
, лежащим в касательной плоскости к поверхности уровня, является прямым.
3. Сила в потенциальном силовом поле всегда направлена в сторону возрастающих значений силовой функции. Для
доказательства этого свойства силы возьмем точку 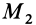 на перпендикуляре к поверхности уровня, восставленном в точку
на перпендикуляре к поверхности уровня, восставленном в точку 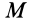 в направлении возрастающих значений силовой функции. Тогда элементарная работа на элементарном перемещении
в направлении возрастающих значений силовой функции. Тогда элементарная работа на элементарном перемещении 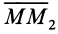 , равном
, равном 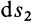 , вычисляется по формуле
, вычисляется по формуле
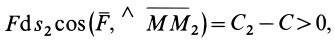
так как 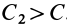 .
.
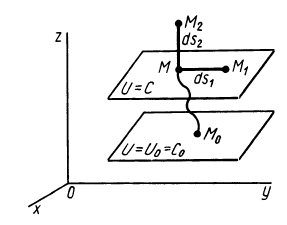
Рис. 73
Следовательно,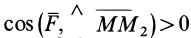 ; поэтому угол, равный
; поэтому угол, равный 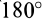 , исключается и получается, что сила
, исключается и получается, что сила 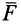 направлена по
направлена по 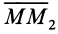 в сторону возрастающих значений силовой функции.
в сторону возрастающих значений силовой функции.
4. Если все силовое поле разбить поверхностями уровня на 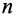 равных значений так, что для первой поверхности уровня
равных значений так, что для первой поверхности уровня 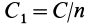 , для второй
, для второй 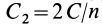 и последней
и последней 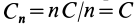 , то там, где соседние поверхности уровня ближе друг к другу, модуль силы
, то там, где соседние поверхности уровня ближе друг к другу, модуль силы 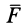 больше, чем в местах, где поверхности уровня дальше отстоят друг от друга. Это свойство можно проверить, если заметить, что работа между точками любых двух соседних поверхностей в этом случае одна и та же. Следовательно, там, где расстояние между поверхностями меньше, сила по числовому значению больше, и наоборот.
больше, чем в местах, где поверхности уровня дальше отстоят друг от друга. Это свойство можно проверить, если заметить, что работа между точками любых двух соседних поверхностей в этом случае одна и та же. Следовательно, там, где расстояние между поверхностями меньше, сила по числовому значению больше, и наоборот.
Рис. 74
Наряду с поверхностями уровня в силовом поле вводят понятие силовой линии, т. е. такой линии, в каждой точке которой сила направлена по касательной к этой линии (рис. 74). Так как вектор  с проекциями на оси
с проекциями на оси  всегда направлен по касательной к кривой, то из условия параллельности
всегда направлен по касательной к кривой, то из условия параллельности 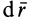 и
и 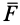 следует, что
следует, что
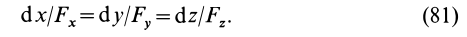
Эти дифференциальные уравнения относительно координат 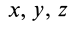 являются дифференциальными уравнениями силовой линии.
являются дифференциальными уравнениями силовой линии.
Потенциальная энергия
В случае потенциального силового поля наряду с силовой функцией можно ввести другую функцию, характеризующую запас энергии в данной точке поля,— потенциальную энергию в этой точке (рис. 75), или потенциальную энергию материальной точки в рассматриваемой точке силового поля.
Потенциальной энергией 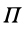 материальной точки в рассматриваемой точке силового поля
материальной точки в рассматриваемой точке силового поля 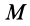 называют работу, которую совершают силы поля, действующие на материальную точку при перемещении ее из точки
называют работу, которую совершают силы поля, действующие на материальную точку при перемещении ее из точки 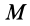 в начальную точку
в начальную точку 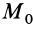 , т. е.
, т. е.
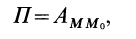
или
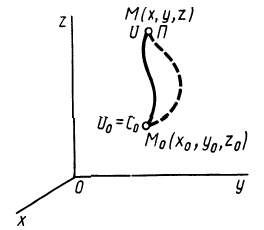
Рис. 75
Постоянная 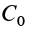 одна и та же для всех точек поля, зависящая от того, какая точка поля выбрана за начальную. Очевидно, что потенциальную энергию можно ввести только для потенциального силового поля, в котором работа не зависит от формы перемещения между точками
одна и та же для всех точек поля, зависящая от того, какая точка поля выбрана за начальную. Очевидно, что потенциальную энергию можно ввести только для потенциального силового поля, в котором работа не зависит от формы перемещения между точками 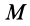 и
и 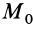 . Непотенциальное силовое поле не имеет потенциальной энергии, для него не существует и силовой функции.
. Непотенциальное силовое поле не имеет потенциальной энергии, для него не существует и силовой функции.
На основании (77) и (82) имеем:
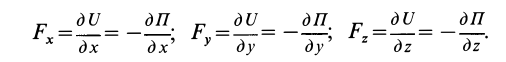
Из (78), (79) и (82) соответственно получаем
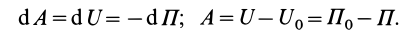
Из приведенных формул следует, что 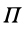 определяется с точностью до произвольной постоянной, которая зависит от выбора начальной точки, но эта произвольная постоянная не влияет на вычисляемые через потенциальную энергию силы и работу этих сил. Учитывая это, формулу (82) можно выразить так:
определяется с точностью до произвольной постоянной, которая зависит от выбора начальной точки, но эта произвольная постоянная не влияет на вычисляемые через потенциальную энергию силы и работу этих сил. Учитывая это, формулу (82) можно выразить так:

или
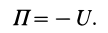
Потенциальную энергию в какой-либо точке поля с точностью до произвольной постоянной можно определить как значение силовой функции в этой же точке, взятое со знаком минус. По существу, достаточно одной из функций 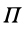 или
или 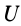 .
.
Понятие потенциальной энергии было введено раньше, чем силовая функция. Силовая функция более удобна, так как некоторые формулы, содеражащие эту функцию, не имеют знака минус.
Примеры вычисления силовых функций
Если вычислить силовую функцию, то на основании (82') будет известна и потенциальная энергия. Вычислим силовые функции однородного поля силы тяжести, силового поля линейной силы упругости и силового поля силы притяжения, действующей по закону Ньютона.
Силовая функция однородного поля силы тяжести. Если ось 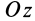 (рис. 76) направить вертикально вверх, то проекции силы тяжести на координатные оси будут равны
(рис. 76) направить вертикально вверх, то проекции силы тяжести на координатные оси будут равны
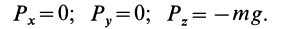
Вычисляя элементарную работу силы 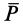 , получаем
, получаем
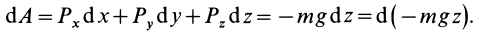
Так как элементарная работа является полным дифференциалом, то силовое поле силы тяжести является потенциальным и силовая функция этого поля определяется по формуле
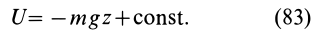
По формуле (83) определяют силовую функцию однородного поля силы тяжести, т. е. поля, в котором сила тяжести постоянна по модулю и направлению. Уравнение поверхности уровня 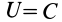 или
или 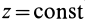 , т.е. поверхностями уровня являются горизонтальные плоскости.
, т.е. поверхностями уровня являются горизонтальные плоскости.
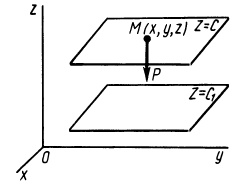
Рис. 76
Силовая функция линейной силы упругости
Для линейной силы упругости (см. рис. 62) имеем:
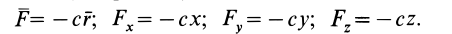
Следовательно
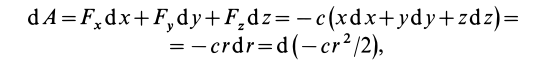
так как 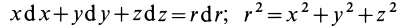 .
.
Силовую функцию линейной силы упругости определяют по формуле
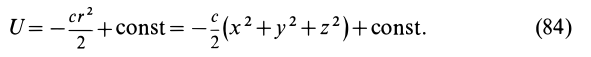
Поверхностями уровня 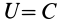 являются сферы
являются сферы 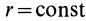 .
.
Силовая функция силы притяжения по закону Ньютона
Вычислим силовую функцию поля земного притяжения. Если выбрать начало координат в центре Земли (рис. 77), то сила притяжения точки земным шаром 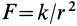 .
.
Сила F направлена к центру Земли; следовательно, вводя единичный вектор 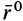 по радиусу-вектору от этого центра в рассматриваемую точку
по радиусу-вектору от этого центра в рассматриваемую точку 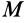 , имеем
, имеем
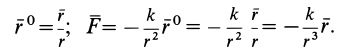
Проецируя силу 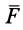 на координатные оси, получаем:
на координатные оси, получаем:
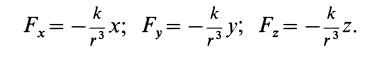
Тогда
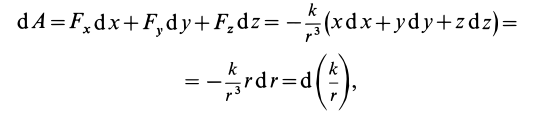
так как 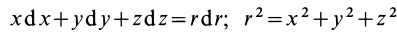 .
.
Рис. 77
Таким образом, силовая функция силы притяжения, по закону Ньютона,
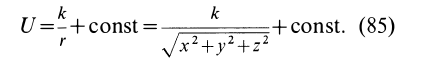
Постоянную 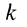 для, случая Земли можно выразить так:
для, случая Земли можно выразить так:
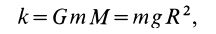
где 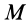 —масса Земли;
—масса Земли; 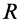 — радиус Земли;
— радиус Земли; 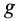 —ускорение силы тяжести на поверхности Земли;
—ускорение силы тяжести на поверхности Земли; 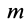 — масса точки;
— масса точки; 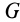 — постоянная тяготения. Если вместо Земли рассматривается другое небесное тело, изменяется только постоянная
— постоянная тяготения. Если вместо Земли рассматривается другое небесное тело, изменяется только постоянная 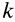 .
.
Силовая функция и потенциальная энергия системы
Для механической системы в потенциальном силовом поле можно ввести силовую функцию как функцию, зависящую от координат всех точек системы, т. е. от положения системы в силовом поле. Если система состоит из 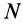 точек, то силовая функция
точек, то силовая функция 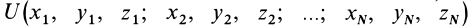 зависит в общем случае от координат всех точек. Проекции силы, действующей на каждую точку системы,
зависит в общем случае от координат всех точек. Проекции силы, действующей на каждую точку системы,
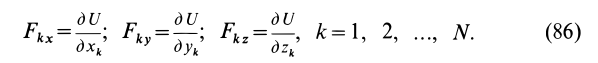
Сумма элементарных работ всех сил, действующих на точки системы, определяется по формуле
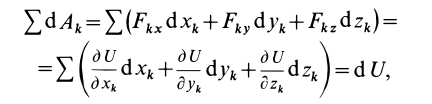
или

Таким образом, сумма элементарных работ сил поля, действующих на механическую систему, равна полному дифференциалу от силовой функции. Если вычислить сумму работ, которую совершат силы поля, действующие на механическую систему при перемещении системы из положения 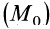 , в котором имеется силовая функция
, в котором имеется силовая функция 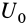 , в положение
, в положение 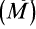 , в котором есть силовая функция
, в котором есть силовая функция 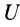 , то
, то
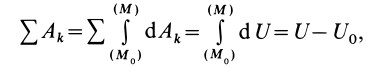
или

Следовательно, сумма работ сил поля, действующих на систему при перемещении системы из одного начального положения в другое, равна разности значений силовой функции в конечном и начальном положениях системы.
Потенциальной энергией системы 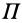 в рассматриваемом положении
в рассматриваемом положении 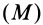 потенциального силового поля называют сумму работ сил поля, действующих на систему, которую эти силы совершают при перемещении системы из рассматриваемого положения в начальное положение
потенциального силового поля называют сумму работ сил поля, действующих на систему, которую эти силы совершают при перемещении системы из рассматриваемого положения в начальное положение 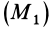 , т. е.
, т. е.
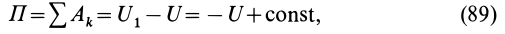
где 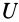 —значение силовой функции для системы сил в положении
—значение силовой функции для системы сил в положении 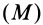 ;
; 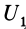 —значение силовой функции в начальном положении.
—значение силовой функции в начальном положении.
Из (86) — (89) следует:
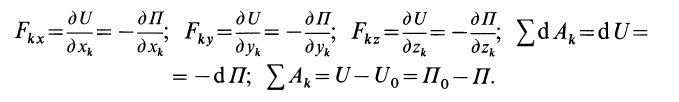
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Закон сохранения механической энергии
- Принцип Даламбера
- Динамические реакции при вращении твердого тела вокруг неподвижной оси
- Векторное исчисление
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Теорема об изменении кинетической энергии