Построение проекций линий пересечения конуса плоскостью с примером

Построение проекций линий пересечения конуса плоскостью:

В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии. Они называются ли­ниями конических сечений.

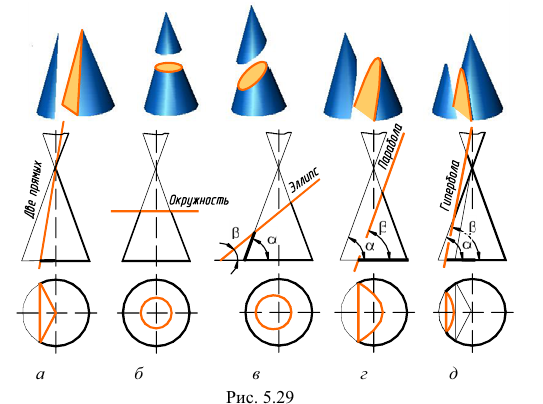
Если секущая плоскость проходит через вершину конуса, в его се­чении получается две прямые - образующие (треугольник) (рис. 5.29, а). В результате пересечения конуса плоскостью, перпендикулярной оси конуса, получается окружность (рис. 5.29, б). Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса могут получиться эллипс, парабола или гипербола (рис. 5.29, в, г, д) - в зависимости от величины угла наклона секущей плоскости.

Эллипс получается в том случае, когда угол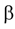

Если углы 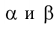равны (то есть секущая плоскость параллельна одной из образующих конуса), в сечении получается парабола (рис. 5.29, г).

Если секущая плоскость направлена под углом, который изменяется в пределах 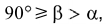то в сечении получается гипербола. В этом случае секущая плоскость параллельна двум образующим конуса. Гипербола имеет две ветви, так как коническая поверхность двухполостная (рис. 5.29, д).

Известно, что точка принадлежит поверхности, если она принадлежит какой-нибудь линии поверхности. Для конуса наиболее простыми линиями являются прямые (образующие) и окружности. Следова­тельно, если требуется найти горизонтальные проекции точек А и В, принадлежащих поверхности конуса, то нужно через точки провести одну из этих линий.

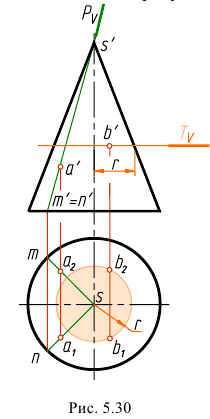
Горизонтальную проекцию точки А найдем с помощью образующей. Для этого через точку А и вершину конуса S проведем вспомогательную фронтально - проецирующую плос­кость 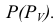Эта плоскость пересекает конус по двум образующим 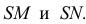Их фронтальные проекции совпадают. Строим горизонтальные проекции образующих. Затем проводим через точку а' линию связи. На пересечении линии связи и горизонтальных проекций образующих определим горизонтальную проекцию точки.

Задача имеет два ответа: точки 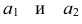. (рис. 5.30).

Горизонтальную проекцию точки В най­дем, построив окружность, на которой она лежит. Для этого через точку проведем горизонтальную плоскость 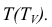Плоскость пересекает конус по окружности радиуса 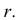Строим горизонтальную проекцию этой окружности. Через точку 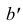проведем линию связи до ее пересечения с окружностью. Зада­ча также имеет два ответа — точки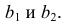

Рассмотрим пример построения проекций линии пересечения конуса фронтально - проецирующей плоскостью 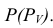В этом случае в сечении получается эллипс (рис. 5.31).

Фронтальная проекция линии сечения совпадает с фронтальным следом плоскости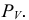

Для удобства решения задачи обозначим крайние образующие конуса и определим характерные (опорные) точки.

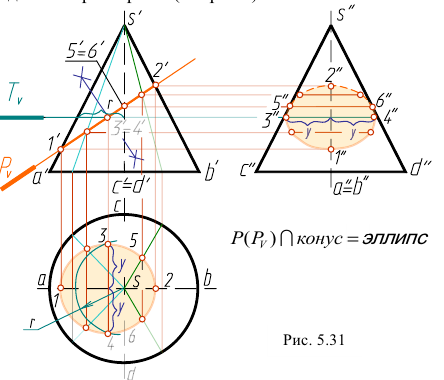
Нижняя точка 1 лежит на образующей AS, верхняя - 2 на образующей BS. Эти точки определяют положение большой оси эллипса. Малая ось эллипса перпендикулярна большой оси. Чтобы найти малую ось, разделим отрезок 1-2 на две равные части. Точки 3 и 4 определяют малую ось эллипса. Точки 5 и 6, расположенные на образующих CS и DS, являются точками границы видимости для профильной плоскости проекций. Проекции точек 1, 2, 5 и 6 находятся на соответствующих проекциях образующих. Чтобы найти проекции точек 3 и 4, проводим дополнительную секущую плоскость 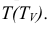Она рассекает конус по окружности радиуса 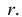На этой окружности находятся проекции данных точек.

На горизонтальную плоскость проекций окружность проецируется в натуральную величину. Проведя линию связи, находим горизонтальные проекции точек 3 и 4. Профильные проекции находим, отложив на линии связи от оси конуса у координаты точек 3 и 4 (рис. 5.3 I).

Для точного построения эллипса недостаточно перечисленных то­чек. Поэтому необходимо определить дополнительные (случайные точ­ки). Проекции этих точек находим аналогично точкам 3 и 4. Их можно найти также проводя через эти точки образующие. Найдя проекции всех точек, соединяем их. Определяем видимость. На горизонтальной плоскости все точки, лежащие на поверхности конуса, видимы. На профильной -точки 5, З, 1,4, 6 видимы, остальные - нет.