Построение падающих теней в начертательной геометрии с примерами

Построение падающих теней на комбинированных поверхностях вращении:

Рассмотрим построение теней на комбинированной поверхности вращения типа «Ваза» (рисунок 12.1). Комбинированная поверхность состоит из тора, цилиндров, сферы, скоции. Для того, чтобы построить, падающие тени, прежде всего необходимо построить собственные тени, так как контур падающей тени, есть тень от контура собственной тени. Построение собственных теней элементов поверхности вазы были рассмотрены в предыдущей лекции №11: тор (рисунок 11.8), цилиндр (рисунок 11.1), сфера (рисунок 11.7), скоция (рисунок 11.9).

Необходимо отметить некоторые закономерности контуров собственных теней:

• -    на линии касания двух разных поверхностей контуры собственных теней этих поверхностей имеют точки перелома (точки
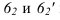
• -    когда две соосные поверхности имеют общую линию пересечения, то контуры собственных теней не будут иметь общей точки (точки

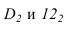
Далее приступаем к построению падающих теней. Тень от контура собственной тени тора 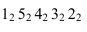падает на освещенную поверхность цилиндра. Для ее построения используется метод вспомогательного осевого экрана. При этом точки 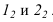лежат на осевом экране. Точка 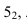лежащая в лучевой плоскости, отбросит тень на ось 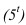. Тень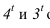от точек 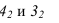строится методом выноса. Контур 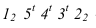- контур тени падающей на фронтальный экран. Пересекая левую образующую цилиндра он дает точку 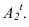. На одной горизонтали с 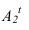находим 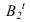на оси. Высшая точка падающей тени 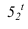определяется следующим образом. Находится горизонталь пересечения конуса с углом образующей 35° с цилиндром. Луч проведенный из точки 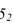под углом 45° с этой горизонталью и дает точку 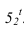Точку - точку 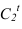исчезновения тени - определяем обратным лучом, построив тень от образующей цилиндра на фронтальный экран. При этом нужно иметь ввиду, что линия контура падающей тени в точке исчезновения 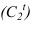должна быть касательна к проекции луча.

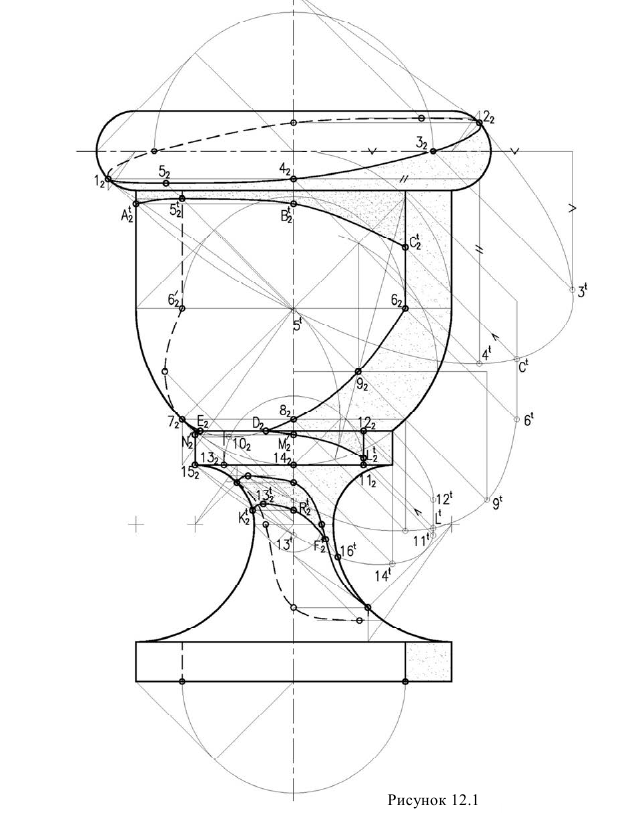
Далее строим тень, падающую от сферы на цилиндр. Тень начинается из точек 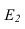и 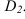Строим тень от сферы на фронтальный экран. Контур тени, пересекая образующую цилиндра, дает точ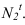ку Точку 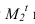находим на оси на одной горизонтали с 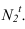Точку 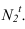определяем обратным лучом, построив тень образующей цилиндра на фронтальный экран. Нужно обратить внимание на то, что контур падающей тени 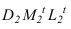будет касательным к линии пересечения поверхностей сферы и цилиндра, а в точке 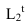касательным к проекции луча. Далее строим тень от нижнего основания цилиндра, падающую на скоцию (тороид). Для этого строим тень от окружности на фронтальный экран -  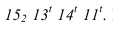Пересекаясь с контуром скоции, она дает точк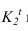и и 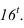. Точка 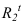лежит на одной горизонтали с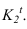. Для нахождения высшей точки падающей тени - 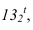точку 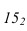соединяем с 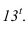Эта прямая является образующей конуса с углом 35°. Строим горизонталь пересечения этого конуса с поверхностью скоции и находим на ней точку пересечения луча проведенного из точки 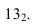Соединяем полученные точки 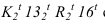с таким расчетом, чтобы в точке исчезновения тени 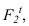контур тени касался проекции луча.

Метод биссекторного экрана

В некоторых случаях для построения падающих теней на поверхностях вращения удобно использовать вспомогательный биссекторный экран. Эта биссекторная плоскость удобна тем, что тень на нее от горизонтальной окружное™ проецируется также окружностью радиуса 0,707 данной. Способ биссекторных экранов применяется в сочетании со способом обратных лучей.

Для примера рассмотрим построения тени от круглой плиты на круглую колонну (рисунок 12.2).

Тень от окружности плиты на биссекторный экран - окружность радиуса R. Тень от левой контурной образующей колонны падает на середину левого радиуса цилиндра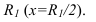

Тень от бликовой образующей колонны 2 надает на ось цилиндра.

Тень от средней образующей 3 падает на середину правого радиуса цилиндра.

Тень образующей 5 совпадает с тенью образующей 3 при обратном луче.

Находим точки пересечения теней образующих, падающих на биссекторный экран, с тенью от плиты и обратными лучами, определяем их положения на соответствующих образующих.

На рисунке 12.2 горизонтальная проекция дана только для пояснения построений. Фактически построения могут быть выполнены только по фронтальной проекции.  

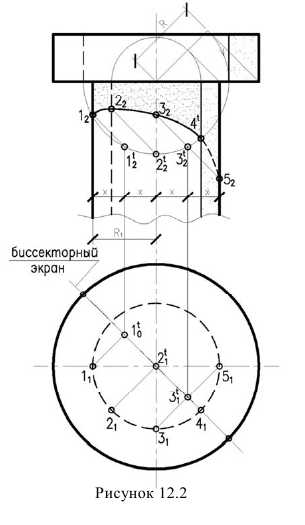
Тень от квадратной плиты на колонну:

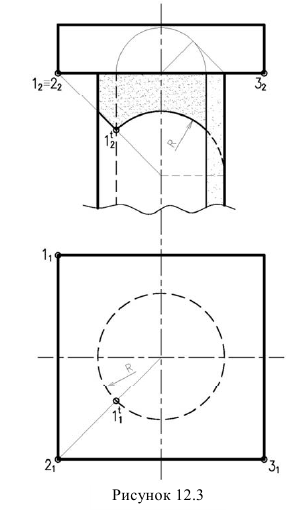
Тень от квадратной плиты на цилиндрическую колонну (рисунок 12.3) фактически является тенью от двух прямых 1-2 - фронтально-проецирующей и 2-3 - профильно-проецирующей (по отношению к фасаду -продольной).

Нам из предыдущего материала известно, что тень от продольной прямой зеркально повторяется план, т.е. является окружностью того же радиуса, что и колонна. А тень от проецирующей прямой совпадает с направлением луча. Поэтому очевидно, что построение тени можно выполнить по одной фронтальной проекции, т.е. фасаду.

• Заказать чертежи

Построение падающих теней на архитектурных деталях:

Тени канители колоны

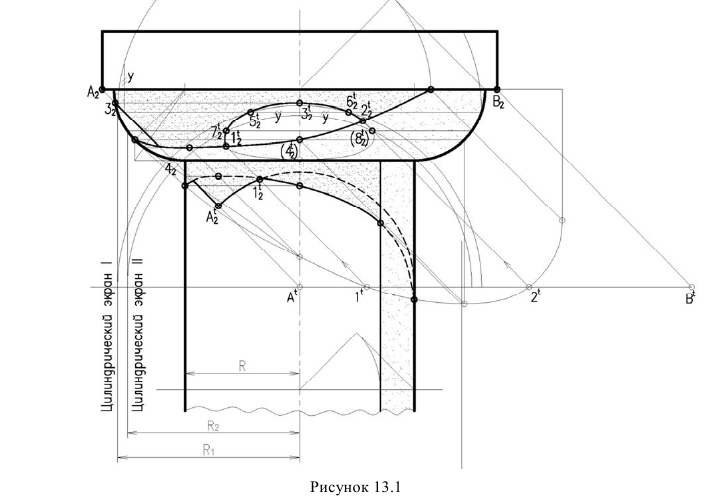
Построение тени капители (рисунок 13.1) представляет собой комплексную задачу, объединяющую ранее построенные тени на отдельных частях. Собственные тени на цилиндре и на валике (тор), падающая тень от валика на колонну (цилиндр) выполнена аналогично рисунку 12.1. А построение падающей тени от квадратной плиты на валик строится способом цилиндрических экранов или глубинных координат. Сначала построим тень, от квадратной плиты падающую на колонну. Построение выполняется аналогично рисунку 12.3. В итоге, контур падающей тени на цилиндрической колонне, складывается из тени падающей от валика и квадратной плиты. Тень от продольной стороны квадрата представляет окружности радиуса R. Тень от проецирующей стороны квадрата совпадает с направлением луча, как на колоне, так и на валике. Необходимо построить тень от продольной стороны квадрата на валик. Точки 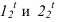- точки исчезновения тени находим обратным лучом с фронтального осевого экрана. Высшую точку 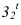и низшую - 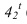(мнимую) находим на параллелях проведенных из точек пересечения тени от проецирующей стороны квадрата на валике. Для построения промежуточных точек контура тени применяем вспомогательные цилиндрические экраны. 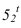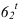Теневые точки и находим на линии пересечения цилиндрического экрана I с валиком, построив тень как на цилиндре радиуса 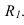. Аналогично строим теневые точки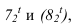применив цилиндрический экран II радиуса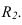Полученные точки соединяем плавной кривой, учитывая, что в точках 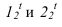лучи будут касательными к полученной кривой.

Промежуточные точки 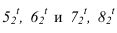можно также получить способом глубинных координат. Для этого берется ряд горизонтальных сечений. На примере сечение показано совпадающим с основанием цилиндрического экрана I. Для дальнейшего построения окружность сечения совмещается с фронтальной плоскостью. Определяется координата у, которая откладывается на линии сечения в обе стороны от оси для получения точек  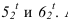Аналогично строятся другие точки.

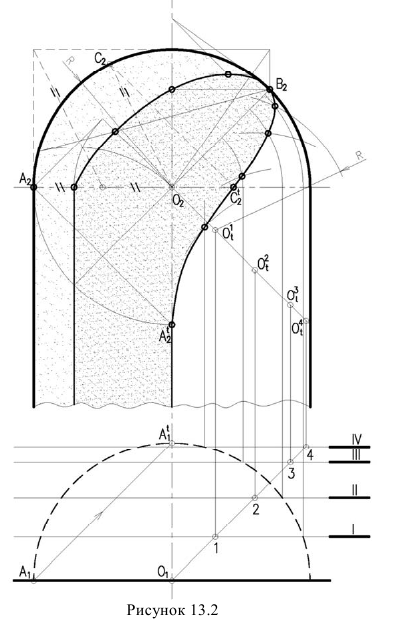
Тени в цилиндрической нише со сферическим верхом (рисунок 13.2)

Прежде всего определяем контур собственной тени известными способами (рисунки 11.1, 11.7) Для построения падающей тени в данной комбинированной нише применяется метод фронтальных экранов. Суть метода заключается в том, что тень от окружности на плоскость ей параллельную является окружностью. Тень от контурной образующей цилиндра, а, следовательно, и от точки А падает на ось цилиндра. Необходимо определить промежуточные точки между 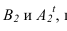, принадлежащие контуру падающей тени от кромки сферической ниши - окружности. Для этого проводим ряд фронтальных экранов 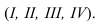Строим линии пересечения фронтальных плоскостей (экранов) с поверхностью ниши. Определяем положение теней от центра окружности кромки ниши О на каждый из экранов. Из теней центров окружности выполняем засечки на соответствующих линиях сечения, радиусом сферы R.

Точка перегиба тени С, на окружности перехода поверхности цилиндра в поверхность сферы, может быть определена следующим образом. Из центра О проводим прямую с уклоном 2:1, которая определит положение точки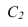 на кромке сферической ниши. Луч проведенный из точки 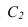даст тень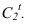

Полученные точки соединяем плавной кривой линией.