Полярные координаты - определение и вычисление с примерами решения

Содержание:

Полярные координаты. параметрические уравнения линии

Полярные координаты

Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.

Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).

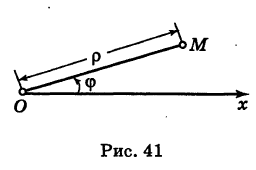
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол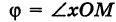

Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.

Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до 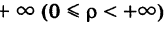и значения ф от 0 до 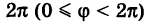, при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие 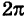, а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.

Связь между прямоугольными и полярными координатами

Рассмотрим переход от полярных координат к прямоугольным и обратно.

Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).

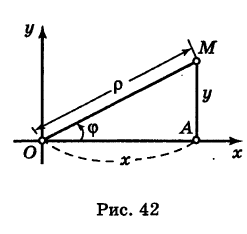
Тогда для произвольной точки М имеем

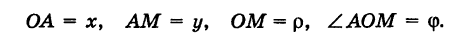
Считая угол ф острым, из прямоугольного треугольника АОМ находим

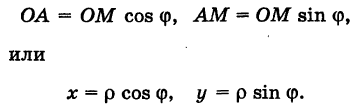
Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем

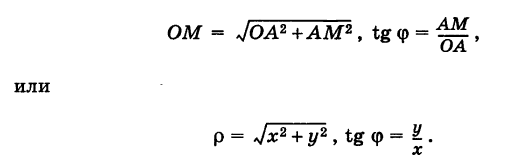
Так выражаются полярные координаты точки через ее прямоугольные координаты.

Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.

Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.

Пример:

Рассмотрим кривую 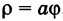, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:

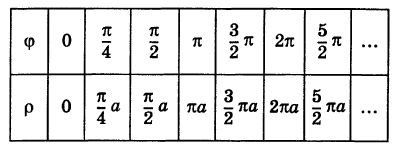
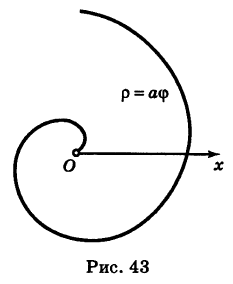
По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).

Параметрические уравнения линии

Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 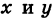, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).

Пример:

Выведем параметрические уравнения окружности.

Пусть М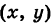 — произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства

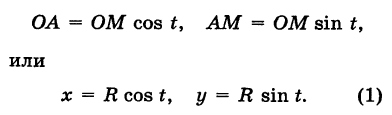
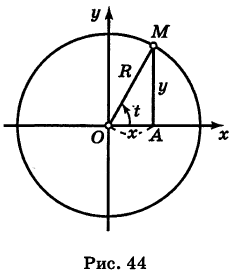
Это и есть параметрические уравнения окружности.

Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:

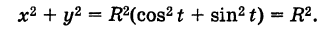
Пример:

Выведем параметрические уравнения эллипса.

Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

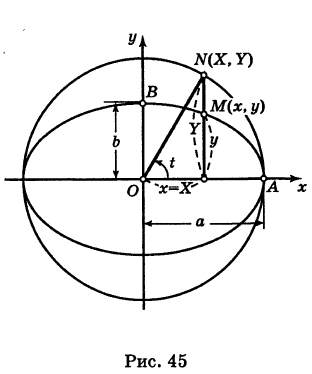За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем

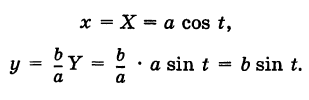
Таким образом, параметрические уравнения эллипса с полуосями а и b есть

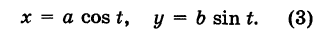Исключив из уравнений (3) параметр получим каноническое уравнение эллипса

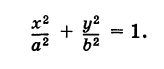
Имея параметрические уравнения линии, можно по точкам построить ее.

Пример:

Построить кривую

Решение:

Составляем таблицу значений:

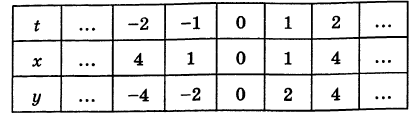
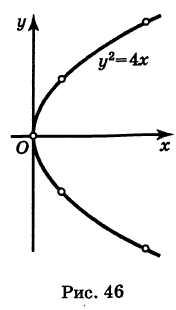Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).

Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 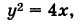т. е. каноническое уравнение параболы.

Параметрические уравнения циклоиды

Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).

Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем

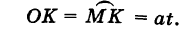
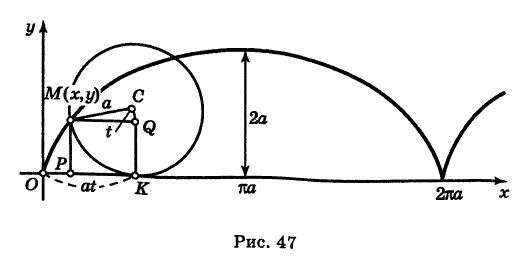
Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:

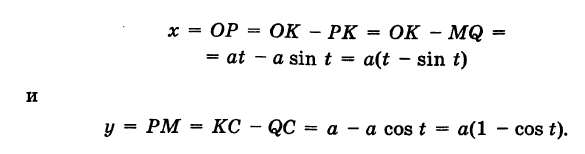
Таким образом, параметрические уравнения циклоиды есть

-------

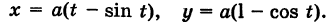
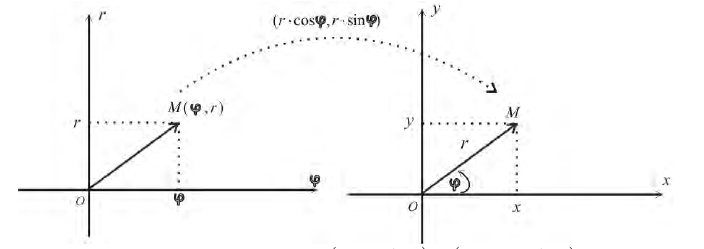
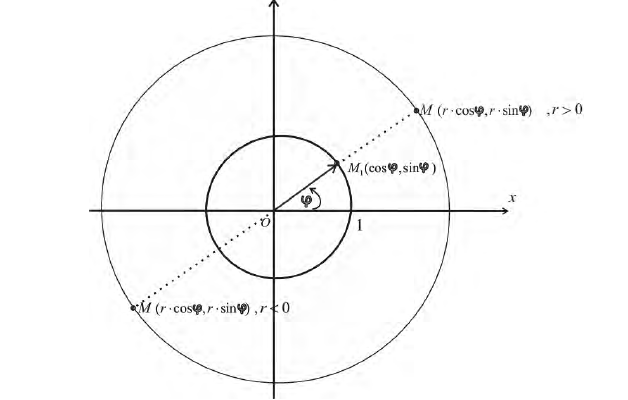
Полярная система координат

Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 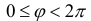. Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 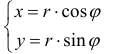    (1)

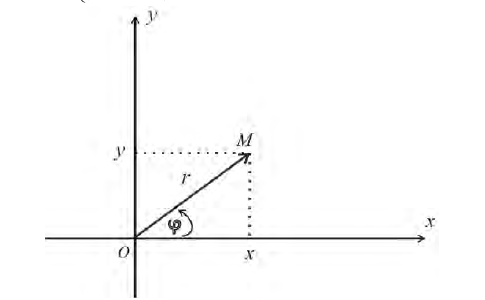
Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:

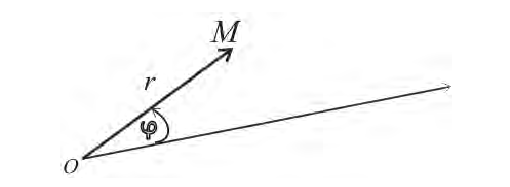
Пример 1.

Построим на плоскости линию, заданную уравнением:
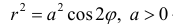− лемниската.
Решение.

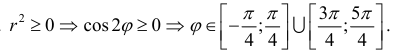
Вычислим значения r при различных значениях ϕ :

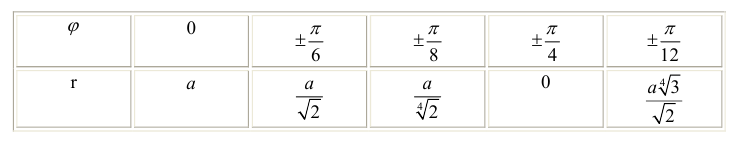
Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :

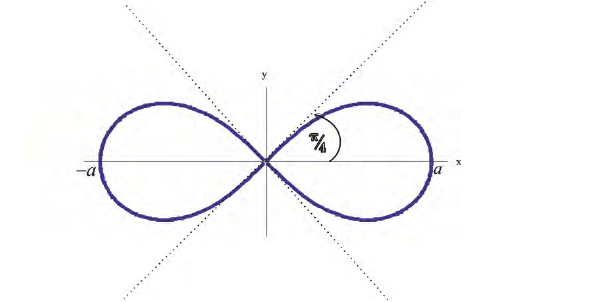
Рис.3. Лемниската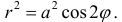 

• Заказать решение задач по высшей математике

Пример 2.

а) Построим кривую 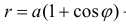 − кардиоида. Рассуждая, как в примере 1 получим:




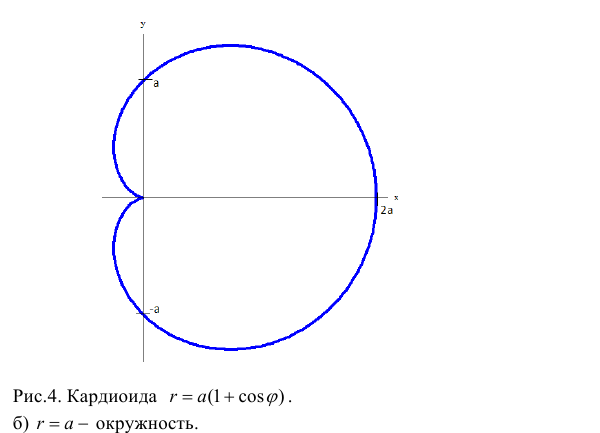
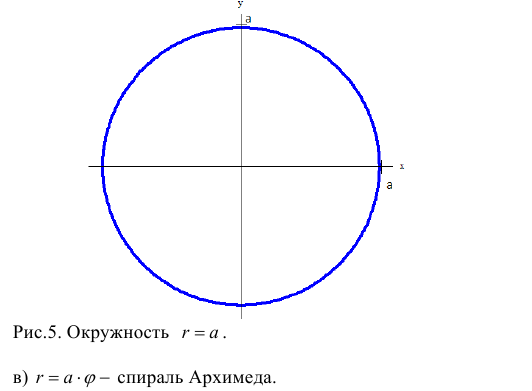
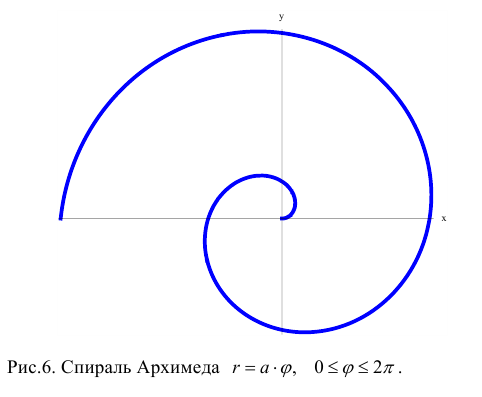
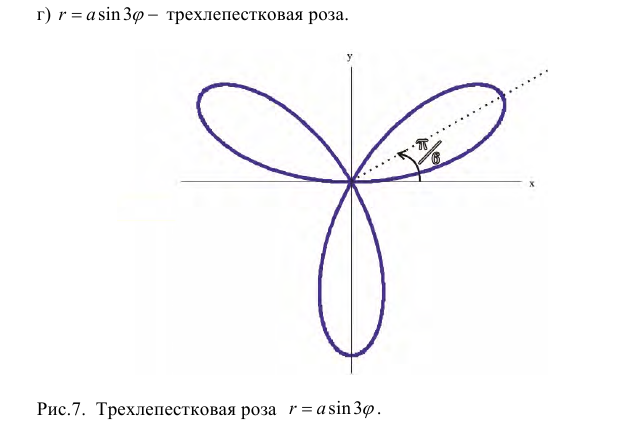
Замечание. Если в определении 1 отбросить требование 0 ≤  ϕ < 2π и не требовать  r > 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).

При этом, если r > 0, то векторы 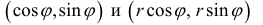сонаправлены, если r<0, то – противоположно направлены:

Тогда, с учетом (1), кривую r= r(ϕ) можно рассматривать как заданную параметрически в виде:
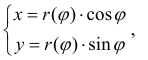ϕ - параметр.
В этом случае на кривой получаются два дополнительных
лепестка, когда  соответствующие случаю r < 0 (см.пример 10 § 17). Фактически, такая кривая – это параметрическая кривая:
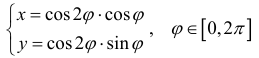 (см.пример 9 § 30).
На кривой 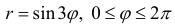каждый из лепестков проходится дважды и
задается параметрически формулами:
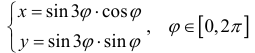(см.пример 10 § 30).

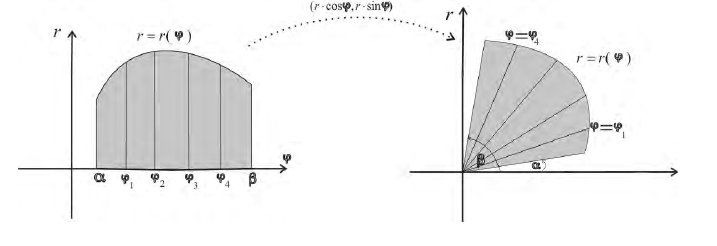
Пусть r = r(ϕ) – кривая в полярной системе координат, r (ϕ) – непрерывна при 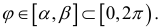. Рассмотрим на плоскости ( x, O, y) криволинейный сектор
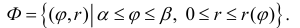Найдем его площадь. Заметим, что сектору Ф
соответствует обычная криволинейная трапеция на плоскости (O, r, ϕ)

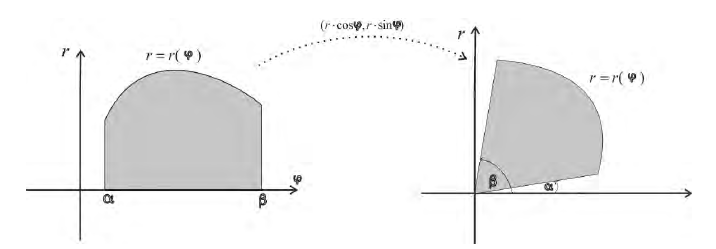
Разобьем фигуру Ф на n частичных фигур лучами На плоскости (O, r, ϕ) получаем обычное разбиение
трапеции:

Рассмотрим, например, нижние суммы Дарбу:

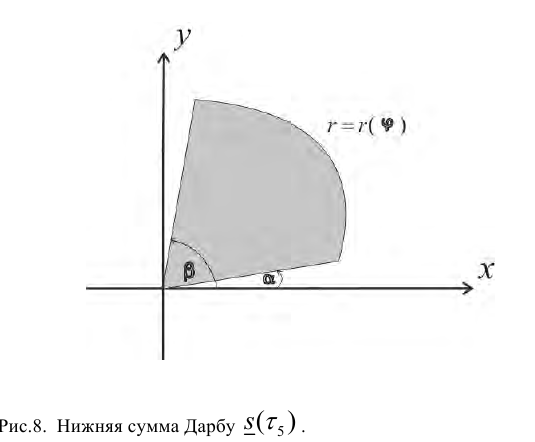
Каждое слагаемое в нижней сумме равно площади  обычного кругового
сектора радиуса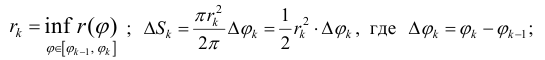  
таким образом,
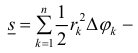 (2) для нижних сумм и 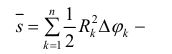(3)    для верхних сумм Дарбу, где  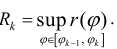Суммы (2) и (3) – суммы Дарбу для функции  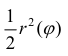(см.формулы (5) § 24), поэтому 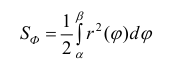(4)
Пример 3.

Найти площадь ограниченную лемнискатой 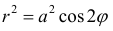 (см.пример 1).
Решение.

По формуле (4):
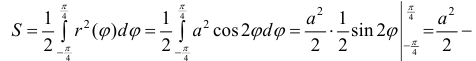площадь одного лепестка.
Поэтому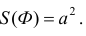 
Пример 4.

Найти площадь фигуры ограниченной линиям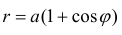и: и 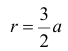 (вне круга).

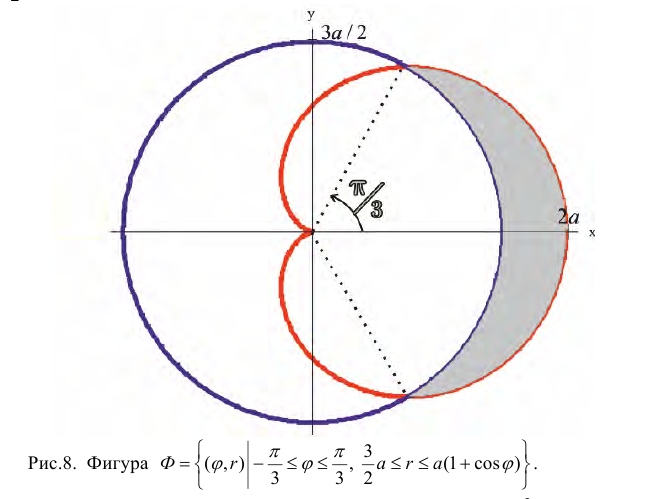
Решение. Найдем точки пересечения кривых: 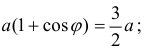 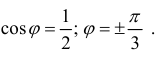   По формуле (4):

Пример 3.

r=2cosϕ. Вычислим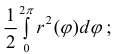 

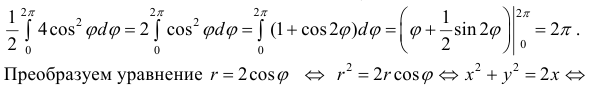
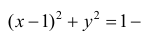− окружность радиуса 1 с центром в точке (1; 0).

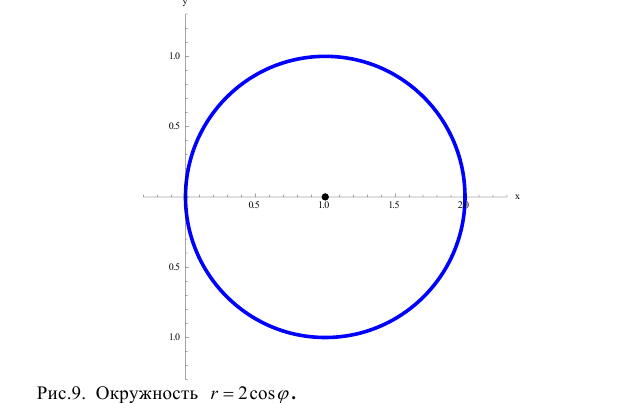
При изменении ϕ от 0 до 2 π окружность проходится дважды и оба раза против
часовой стрелки, поэтому (см. § 30) найденное значение интеграла задает
удвоенную площадь круга.