
Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:

Уравнения такого вида принято называть показательными.
Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Следствие:
Пусть 
Каждому значению показательной функции  соответствует единственный показатель s.
соответствует единственный показатель s.
Пример:
Решить уравнение

Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению

откуда

Ответ: 2; 3.
Пример:
Решить уравнение:

Решение:
а) Данное уравнение равносильно (поясните почему) уравнению

Если степени с основанием 3 равны, то равны и их показатели:

Решив это уравнение, получим


Ответ: 
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решить уравнение:

Решение:
а) Данное уравнение равносильно уравнению

Решая его, получаем:

Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е.  откуда находим
откуда находим 
б) Разделив обе части уравнения на  получим уравнение
получим уравнение  равносильное данному. Решив его, получим
равносильное данному. Решив его, получим 

Ответ: 
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение 
Решение:
Обозначим  тогда
тогда 
Таким образом, из данного уравнения получаем

откуда находим: 
Итак, с учетом обозначения имеем:

Ответ: 1; 2.
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение 
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Ответ: 2.
Пример:
Решить уравнение 
Решение:

Ответ: 3; 4.
Пример:
При каком значении а корнем уравнения  является число, равное 2?
является число, равное 2?
Решение:
Поскольку х = 2 — корень, то верно равенство

Решив это уравнение, найдем

Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества: 

Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду  . Отсюда
. Отсюда 
Пример №1
Решите уравнение 
Решение:
Заметим, что  и перепишем наше уравнение в виде
и перепишем наше уравнение в виде

Применив тождество (1), получим Зх - 7 = -7х + 3, х = 1.
Ответ: 1.
Пример №2
Решить уравнение 
Решение:
Переходя к основанию степени 2, получим:

Согласно тождеству (2), имеем 
Последнее уравнение равносильно уравнению 4х-19 = 2,5х. 
2 Введение новой переменной.
Пример №3
Решить уравнение 
Решение:
Применив тождество 2, перепишем уравнение как 
Введем новую переменную:  Получим уравнение
Получим уравнение 
которое имеет корни  Однако корень
Однако корень не удовлетворяет условию
не удовлетворяет условию  Значит,
Значит, 
Ответ: х=2.
Пример №4
Решить уравнение 
Решение:
Разделив обе части уравнения на  получим:
получим:

последнее уравнение запишется так: 
Решая уравнение, найдем 
Значение  не удовлетворяет условию
не удовлетворяет условию  Следовательно,
Следовательно,

Пример №5
Решить уравнение 
Решение:
Заметим что  Значит
Значит 
Перепишем уравнение в виде 
Обозначим  Получим
Получим 
Получим 
Корнями данного уравнения будут 
Следовательно, 
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение 
Решение:
После вынесения за скобку в левой части  , а в правой
, а в правой  , получим
, получим  Разделим обе части уравнения на
Разделим обе части уравнения на  получим
получим 

Системы простейших показательных уравнений
Пример №7
Решите систему уравнений: 
Решение:
По свойству степеней система уравнений равносильна следующей
системе : Отсюда получим систему
Отсюда получим систему 
Очевидно, что последняя система имеет решение 
Пример №8
Решите систему уравнений: 
Решение:
По свойству степеней система уравнений равносильна следующей системе:  Последняя система, в свою очередь, равносильна системе:
Последняя система, в свою очередь, равносильна системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем  Подставив полученное значение во второе уравнение, получим
Подставив полученное значение во второе уравнение, получим 

Пример №9
Решите систему уравнений: 
Решение:
Сделаем замену:  Тогда наша система примет вид:
Тогда наша система примет вид: 
Очевидно, что эта система уравнений имеет решение 
Тогда получим уравнения 

Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть  . Тогда внутри этого отрезка существует хотя бы одно решение уравнения Дх)=0. Это означает, что существует такое
. Тогда внутри этого отрезка существует хотя бы одно решение уравнения Дх)=0. Это означает, что существует такое  (читается как "кси"), что
(читается как "кси"), что 
Это утверждение проиллюстрировано на следующем чертеже.

Рассмотрим отрезок  содержащий лишь один корень уравнения .
содержащий лишь один корень уравнения .
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности 
Для этого:
- вычисляется значение f(х) выражения

- отрезок делится пополам, то есть вычисляется значение

- вычисляется значение
 выражения f(х) в точке
выражения f(х) в точке 
- проверяется условие

- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину); - если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие

- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:

Для нахождения интервала, содержащего корень уравнения  вычисляются значения
вычисляются значения 
Оказывается, что для корня  данного уравнения выполнено неравенство. Значит, данное уравнение имеет хотя бы один корень, принадлежащий интервалу (-1 -А; 1+А). Для приближенного вычисления данного корня найдем целые
данного уравнения выполнено неравенство. Значит, данное уравнение имеет хотя бы один корень, принадлежащий интервалу (-1 -А; 1+А). Для приближенного вычисления данного корня найдем целые  и
и  удовлетворяющие неравенству
удовлетворяющие неравенству 
Пример №10
Найдите интервал, содержащий корень уравнения 
Решение:
Поделив обе части уравнения на 2 , получим, 
Так как, для нового уравнения 
Значит, в интервале,  уравнение имеет хотя бы один корень. В то же время уравнение при
уравнение имеет хотя бы один корень. В то же время уравнение при  не имеет ни одного корня, так как,
не имеет ни одного корня, так как,
 выполняется. Значит, корень уравнения лежит в (-2,5; 0). Для уточнения этого интервала положим
выполняется. Значит, корень уравнения лежит в (-2,5; 0). Для уточнения этого интервала положим  Для
Для  проверим выполнение условия
проверим выполнение условия


Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство  корень уравнения принадлежит интервалу
корень уравнения принадлежит интервалу
 Пусть
Пусть Если
Если  приближенный
приближенный
корень уравнения с точностью  . Если
. Если  то корень лежит в интервале
то корень лежит в интервале  если
если то корень лежит в интервале
то корень лежит в интервале  . Продолжим процесс до нахождения приближенного значения корня с заданной точностью.
. Продолжим процесс до нахождения приближенного значения корня с заданной точностью.
Пример №11
Найдите приближенное значение корня уравнения  с заданной точностью
с заданной точностью
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что  заключаем, что корень лежит в интервале (-0,5; 0).
заключаем, что корень лежит в интервале (-0,5; 0).
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| < 0,1, то х=-0,25 - приближенное значение корня с точностью 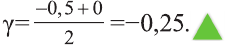
Решение показательных неравенств
Рассмотрим неравенства, в которых переменная (неизвестное) находится в показателе степени. Например, 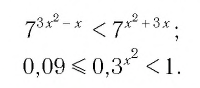
Неравенства такого вида принято называть показательными.
Из теоремы о свойствах показательной функции (п. 2.2, свойство 8) получаем следствие, которое постоянно используется при решении показательных неравенств.
Следствие:
Пусть а > 1. Если 
Пусть 
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0 < а < 1 большему значению функции соответствует меньшее значение аргумента.
При решении показательных неравенств, так же как и при решении показательных уравнений, приходится использовать представление обеих частей неравенства в виде степеней с одним и тем же основанием, разложение одной из частей неравенства на множители, введение новой переменной.
Пример:
Решить неравенство 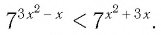
Решение:
Поскольку из двух степеней с основанием 7 больше та, показатель которой больше, то данное неравенство равносильно неравенству
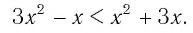
Решим его:
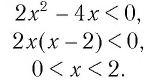
Ответ: (0; 2).
Пример:
Решить неравенство 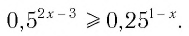
Решение:
Данное неравенство равносильно неравенству
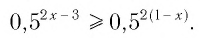
Поскольку из двух степеней с одинаковым основанием 0,5 больше та, показатель которой меньше, то имеем
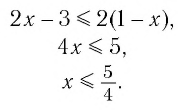
Ответ: 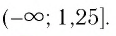
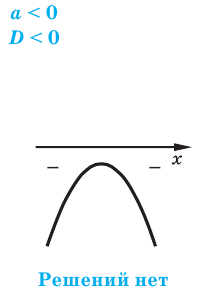
Пример:
Решить неравенство 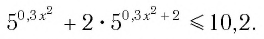
Решение:
Данное неравенство равносильно неравенству
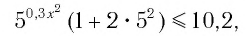
откуда
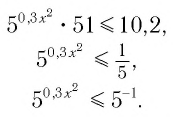
Поскольку из двух степеней с основанием 5 больше та, показатель которой больше, то данное неравенство равносильно неравенству
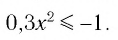
Решений нет, так как 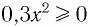 при любых значениях х.
при любых значениях х.
Ответ: нет решений.
Пример:
Решить неравенство
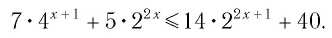
Решение:
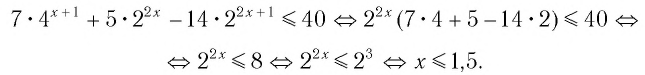
Ответ: 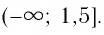
Пример:
Решить неравенство 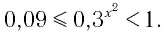
Решение:
Данное неравенство перепишем в виде 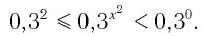
Поскольку из двух степеней с основанием 0,3 больше та, показатель которой меньше, то имеем:
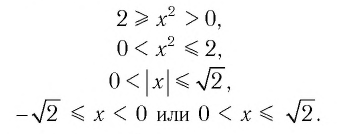
Ответ: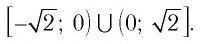
Пример:
Решить неравенство
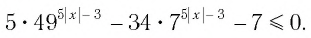
Решение:
Пусть 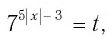 тогда
тогда 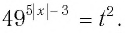 Использовав эти обозначения для данного неравенства, получим
Использовав эти обозначения для данного неравенства, получим 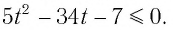
Решив это неравенство, получим: 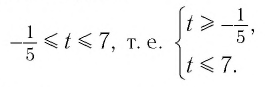 Поскольку
Поскольку 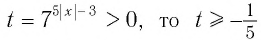 при любых значениях х.
при любых значениях х.
Остается решить второе неравенство системы:
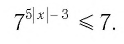
Получим:
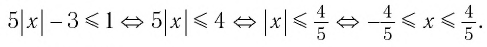
Ответ: 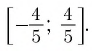
Пример:
При каких значениях m любое значение х из промежутка [9; 10] является решением неравенства
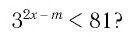
Решение:
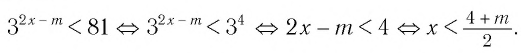 Чтобы решением неравенства
Чтобы решением неравенства 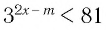 являлось любое значение х из промежутка
являлось любое значение х из промежутка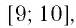 необходимо, чтобы промежуток
необходимо, чтобы промежуток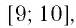 входил во множество решений данного неравенства, т. е. в промежуток
входил во множество решений данного неравенства, т. е. в промежуток 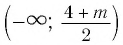 (рис.33).
(рис.33).
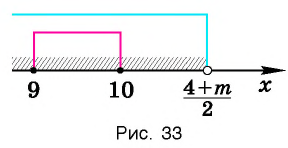
Итак, имеем:
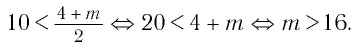
Показательные уравнения, неравенства и их системы
При решении показательных уравнений и неравенств, т. е. уравнений и неравенств, в которых переменная содержится в показателе степени, используются свойства показательной функции:
- областью значений показательной функции
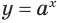 является множество всех положительных действительных чисел;
является множество всех положительных действительных чисел; - если
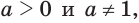 то условия
то условия 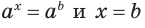 являются равносильными;
являются равносильными; - при
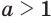 показательная функция
показательная функция 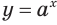 является возрастающей, а при
является возрастающей, а при 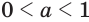 — убывающей.
— убывающей.
Пример №12
Решим уравнение:
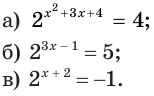
а) 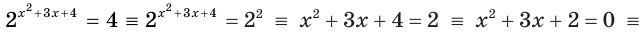
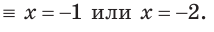
Ответ. -1; -2.
б) 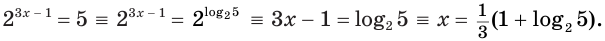
Ответ. 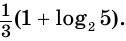
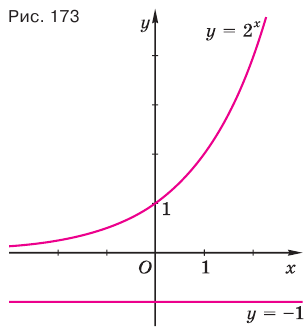
в) Поскольку число -1 не принадлежит области значений показательной функции 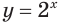 , то уравнение
, то уравнение 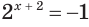 не имеет корней (рис. 173).
не имеет корней (рис. 173).
Ответ. Корней нет.
Пример №13
Решим неравенство:
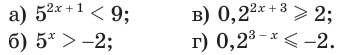
а) 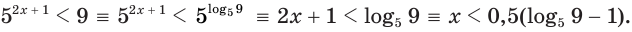
Ответ. 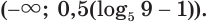
Здесь при переходе от неравенства 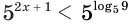 к неравенству
к неравенству 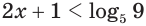 мы сохранили знак неравенства, так как основание степени больше единицы.
мы сохранили знак неравенства, так как основание степени больше единицы.
б) Поскольку значениями показательной функции 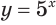 являются положительные числа, то условие
являются положительные числа, то условие 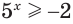 истинно при любом значении показателя, т. е. каждое действительное число является решением этого неравенства.
истинно при любом значении показателя, т. е. каждое действительное число является решением этого неравенства.
Ответ. 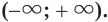
в) 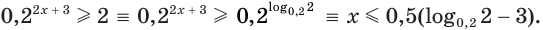
Ответ. 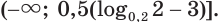
Здесь при переходе от неравенства 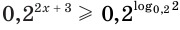 к неравенству
к неравенству 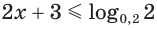 мы изменили знак неравенства на противоположный, так как основание степени меньше единицы.
мы изменили знак неравенства на противоположный, так как основание степени меньше единицы.
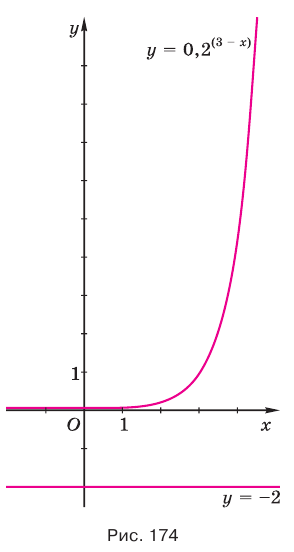
г) Поскольку при любом значении показателя 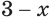 значением выражения
значением выражения 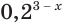 является положительное число, то неравенство
является положительное число, то неравенство 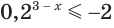 не может быть истинным ни при каком значении переменной
не может быть истинным ни при каком значении переменной  , т. е. оно не имеет решений (рис. 174).
, т. е. оно не имеет решений (рис. 174).
Для сведения показательного уравнения или неравенства к простейшим применяют общие приемы решения уравнений и неравенств: введение вспомогательной переменной, использование графических представлений, использование свойств функций, разложение на множители.
Пример №14
Решим уравнение:

а) Пусть 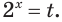 Тогда уравнение
Тогда уравнение 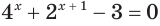 запишется в виде
запишется в виде 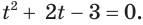 Числа 1 и -3 — его корни. Вернувшись к исходной переменной, получим уравнения
Числа 1 и -3 — его корни. Вернувшись к исходной переменной, получим уравнения 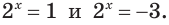 Корнем первого является число 0, а второе уравнение корней не имеет.
Корнем первого является число 0, а второе уравнение корней не имеет.
Ответ. 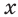 = 0.
= 0.
б) Перед введением вспомогательной переменной разделим обе части уравнения 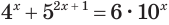 на выражение
на выражение 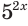 , которое положительно при любых значениях переменной. Будем иметь:
, которое положительно при любых значениях переменной. Будем иметь:
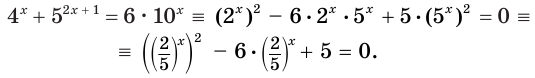
Пусть 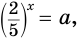 тогда получим уравнение
тогда получим уравнение 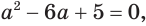 корнями которого являются числа 1 и 5. Значит,
корнями которого являются числа 1 и 5. Значит, 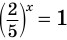 или
или 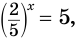 откуда
откуда 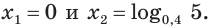
Ответ. 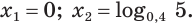
Пример №15
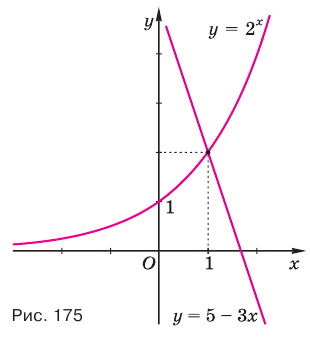
Решим неравенство 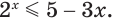
Построим графики функций 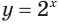 и
и 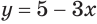 (рис. 175) и найдем, при каких значениях аргумента
(рис. 175) и найдем, при каких значениях аргумента 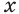 точка графика первой функции лежит ниже точки графика второй. Видим, что графики пересекаются в точке (1; 2). Если
точка графика первой функции лежит ниже точки графика второй. Видим, что графики пересекаются в точке (1; 2). Если 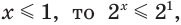 а
а 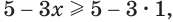 так как функция
так как функция 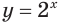 возрастает, а функция
возрастает, а функция 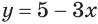 убывает. Значит, при
убывает. Значит, при 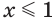 истинно неравенство
истинно неравенство 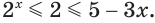 А если
А если 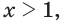 то
то 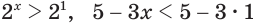 и потому истинно неравенство
и потому истинно неравенство 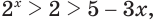 из которого следует, что ни одно число, большее 1, не является решением данного неравенства.
из которого следует, что ни одно число, большее 1, не является решением данного неравенства.
Ответ. 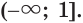
Пример №16
Решим неравенство 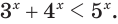
Функции, определяемые выражениями, записанными в левой и правой частях уравнения, возрастающие, но возрастают они с разной скоростью. Используем это. Разделим обе части неравенства на выражение 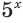 , которое всегда положительно. Получим равносильное неравенство
, которое всегда положительно. Получим равносильное неравенство 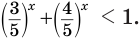 Функция
Функция 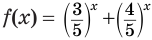 является убывающей как сумма убывающих функций. А поскольку
является убывающей как сумма убывающих функций. А поскольку 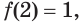 то решениями данного неравенства являются все числа, большие 2.
то решениями данного неравенства являются все числа, большие 2.
Ответ. 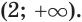
Пример №17
Решим уравнение 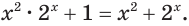
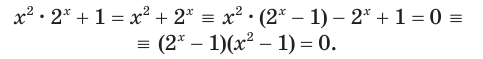
Остается решить уравнения 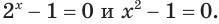 Их корни 0, -1 и 1 исчерпывают все корни исходного уравнения.
Их корни 0, -1 и 1 исчерпывают все корни исходного уравнения.
Ответ. 0; -1; 1.
Пример №18
Решим систему уравнений 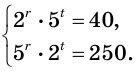
Перемножив уравнения системы, получим уравнение 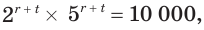 которое равносильно уравнению
которое равносильно уравнению 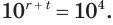 Значит,
Значит, 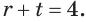
Разделив первое уравнение системы на второе, придем к уравнению 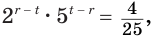 которое равносильно уравнению
которое равносильно уравнению 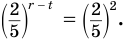 Потому
Потому 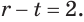
Таким образом, данная система равносильна системе 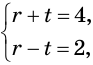 которая имеет решением пару (3; 1).
которая имеет решением пару (3; 1).
Ответ. (3; 1).
Пример №19
Решим систему 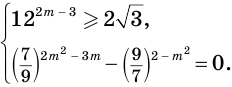
Решим уравнение системы:
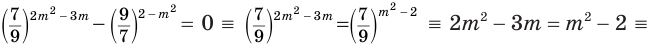
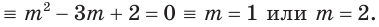
Из найденных чисел неравенству удовлетворяет только число 2.
Ответ. 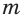 = 2.
= 2.
Пример №20
Решим уравнение 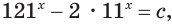 где
где 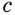 — некоторое число.
— некоторое число.
Данное уравнение равносильно уравнению 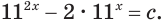 Оно заменой
Оно заменой 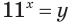 сводится к квадратному уравнению
сводится к квадратному уравнению 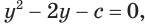 решение которого зависит от дискриминанта
решение которого зависит от дискриминанта 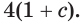
Пусть 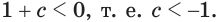 Тогда квадратное уравнение не имеет корней, а потому не имеет корней и исходное уравнение.
Тогда квадратное уравнение не имеет корней, а потому не имеет корней и исходное уравнение.
Пусть 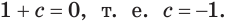 Тогда квадратное уравнение имеет один корень
Тогда квадратное уравнение имеет один корень 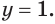 Учитывая замену
Учитывая замену 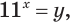 получим уравнение
получим уравнение 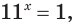 корнем которого является число
корнем которого является число 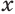 = 0.
= 0.
Пусть 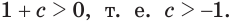 Тогда квадратное уравнение имеет два корня:
Тогда квадратное уравнение имеет два корня: 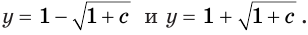 Возвращение к исходной переменной приводит к уравнениям:
Возвращение к исходной переменной приводит к уравнениям: 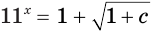 и
и 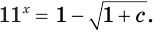 Корнем первого уравнения является число
Корнем первого уравнения является число 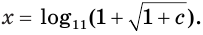 Второе уравнение имеет корнем число
Второе уравнение имеет корнем число 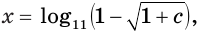 но при условии, что
но при условии, что 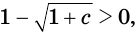 т. е. при
т. е. при 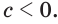
Ответ. Если 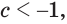 то уравнение не имеет корней;
то уравнение не имеет корней;
если 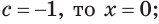
если 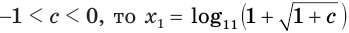
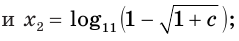
если 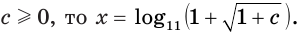
Степень с произвольным действительным показателем
Теперь мы выясним, что представляет собой степень положительного числа с действительным показателем.
Строгое определение степени с действительным показателем и доказательство ее свойств выходит за пределы школьного курса. Текст этого пункта содержит лишь общие пояснения того, как можно провести необходимые обоснования.
Начнем с частного случая. Выясним, что понимают под степенью числа 2 с показателем 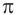 .
.
Иррациональное число 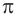 можно представить в виде бесконечной непериодической десятичной дроби:
можно представить в виде бесконечной непериодической десятичной дроби: 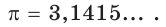
Рассмотрим последовательность рациональных чисел
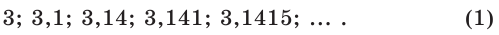
Понятно, что эта последовательность сходится к числу 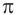 .
.
В соответствии с последовательностью 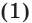 построим последовательность степеней с рациональными показателями:
построим последовательность степеней с рациональными показателями:
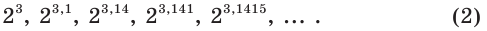
Можно показать, что члены последовательности 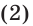 с увеличением номера стремятся к некоторому положительному числу. Это число и называют степенью числа 2 с показателем
с увеличением номера стремятся к некоторому положительному числу. Это число и называют степенью числа 2 с показателем 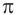 и обозначают 2
и обозначают 2 .
.
Аналогично можно действовать в общем случае, определяя смысл выражения 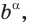 где
где 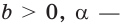 любое действительное число. Для числа
любое действительное число. Для числа 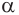 строят сходящуюся к нему последовательность рациональных чисел
строят сходящуюся к нему последовательность рациональных чисел 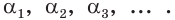 Далее рассматривают последовательность
Далее рассматривают последовательность 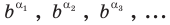 степеней с рациональными показателями (напомним, что степень положительного числа с рациональным показателем определена). Можно доказать, что эта последовательность сходится к положительному числу
степеней с рациональными показателями (напомним, что степень положительного числа с рациональным показателем определена). Можно доказать, что эта последовательность сходится к положительному числу 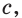 которое не зависит от выбора сходящейся к
которое не зависит от выбора сходящейся к 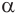 последовательности рациональных чисел
последовательности рациональных чисел 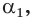
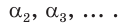 Число
Число 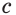 называют степенью положительного числа
называют степенью положительного числа 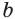 с действительным показателем
с действительным показателем 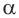 и обозначают
и обозначают 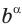 .
.
Если основание 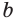 равно единице, то
равно единице, то 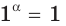 для всех действительных
для всех действительных 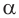 .
.
Если основание 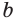 равно нулю, то степень
равно нулю, то степень 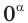 определяют только для
определяют только для 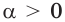 и считают, что
и считают, что 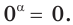 Например,
Например, 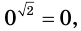
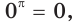 а выражение
а выражение 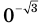 не имеет смысла.
не имеет смысла.
При 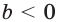 выражение
выражение 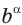 , где
, где 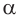 — иррациональное число, не имеет смысла.
— иррациональное число, не имеет смысла.
Степень с действительным показателем обладает теми же свойствами, что и степень с рациональным показателем.
В частности, для 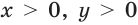 и любых действительных
и любых действительных 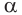 и
и 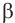 справедливы такие равенства:
справедливы такие равенства:
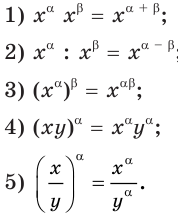
Докажем, например, свойство 1.
Пусть 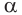 и
и 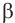 — действительные числа, причем
— действительные числа, причем 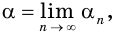
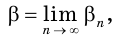
где 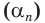 и
и 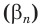 — последовательности рациональных чисел. Имеем:
— последовательности рациональных чисел. Имеем:
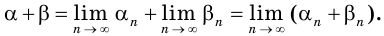
Для положительного числа 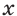 рассмотрим три последовательности:
рассмотрим три последовательности: 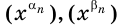 и
и 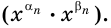
Имеем: 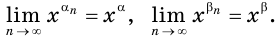
Так как для рациональных показателей 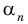 и
и 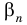 свойство 1 имеет место (мы узнали об этом при изучении свойств степени с рациональным показателем), то
свойство 1 имеет место (мы узнали об этом при изучении свойств степени с рациональным показателем), то 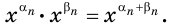
Последовательность рациональных чисел 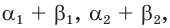
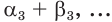 сходится к числу
сходится к числу 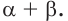 Поэтому можно записать, что
Поэтому можно записать, что 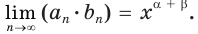
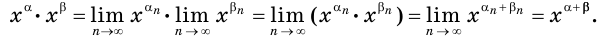
Пример №21
Упростите выражение 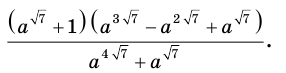
Решение:
Имеем:
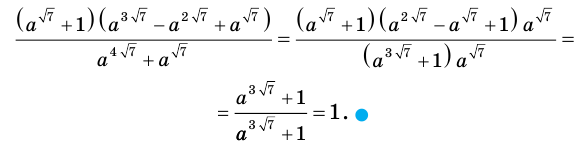
Выберем некоторое положительное число 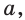 отличное от 1. Каждому действительному числу
отличное от 1. Каждому действительному числу 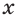 можно поставить в соответствие положительное число
можно поставить в соответствие положительное число 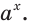 Тем самым задана функция
Тем самым задана функция 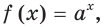 где
где 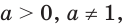 с областью определения
с областью определения 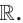 Эту функцию называют показательной функцией. Изучим некоторые свойства показательной функции. При
Эту функцию называют показательной функцией. Изучим некоторые свойства показательной функции. При 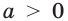 и любом
и любом 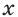 выполняется неравенство
выполняется неравенство 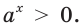 Поэтому область значений показательной функции состоит только из положительных чисел.
Поэтому область значений показательной функции состоит только из положительных чисел.
Можно показать, что для данного числа 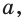 где
где 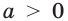 и
и 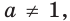 и для любого положительного числа
и для любого положительного числа 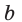 существует такое число
существует такое число 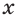 , что выполняется равенство
, что выполняется равенство 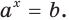
Сказанное означает, что областью значений показательной функции является множество 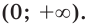
Показательная функция не имеет нулей, и промежуток 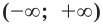 является ее промежутком знакопостоянства.
является ее промежутком знакопостоянства.
Показательная функция непрерывна.
Покажем, что при 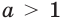 показательная функция является возрастающей. Для этого воспользуемся леммой.
показательная функция является возрастающей. Для этого воспользуемся леммой.
Лемма. Если 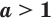 и
и 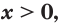 то
то 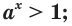 если
если 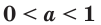 и
и 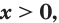 то
то 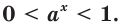
Например, 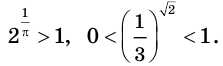
Рассмотрим произвольные числа  и
и  такие, что
такие, что  и функцию
и функцию 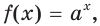 где
где 
Поскольку 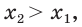 то
то 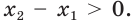 Тогда согласно лемме имеем:
Тогда согласно лемме имеем: 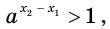 то есть
то есть 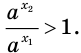 . Так как
. Так как 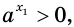 то
то 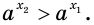
Отсюда 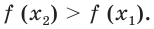
Мы показали, что из неравенства 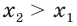 следует неравенство
следует неравенство 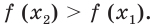 Это означает, что функция
Это означает, что функция 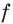 является возрастающей.
является возрастающей.
Аналогично можно показать, что при 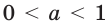 показательная функция является убывающей. Поскольку показательная функция является либо возрастающей (при
показательная функция является убывающей. Поскольку показательная функция является либо возрастающей (при 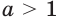 ), либо убывающей (при
), либо убывающей (при 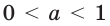 ), то она не имеет точек экстремума.
), то она не имеет точек экстремума.
Показательная функция является дифференцируемой. Подробнее о производной показательной функции вы узнаете в п. 23.
На рисунках 16.1 и 16.2 схематически изображен график показательной функции для случаев 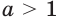 и
и 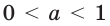 соответственно.
соответственно.
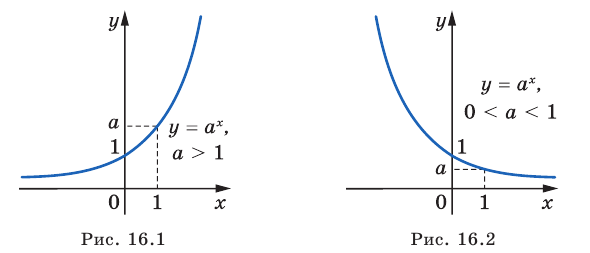
В частности, на рисунках 16.3 и 16.4 изображены графики функций 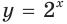 и
и 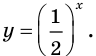
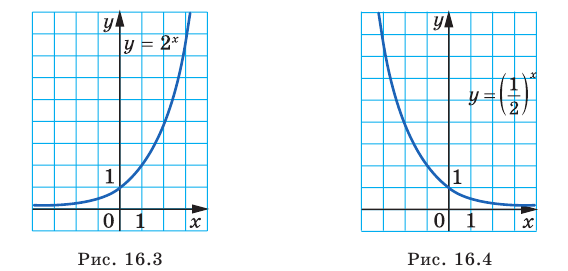
Заметим, что при 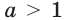 график показательной функции имеет горизонтальную асимптоту
график показательной функции имеет горизонтальную асимптоту  при
при  Аналогично при
Аналогично при 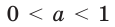 график показательной функции имеет горизонтальную асимптоту
график показательной функции имеет горизонтальную асимптоту 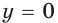 при
при 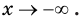
Показательная функция является математической моделью целого ряда процессов, происходящих в природе и в деятельности человека.
Например, биологам известно, что колония бактерий в определенных условиях за равные промежутки времени увеличивает свою массу в одно и то же количество раз.
Это означает, что если, например, в момент времени 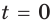 масса была равной 1, а в момент времени
масса была равной 1, а в момент времени 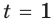 масса была равной
масса была равной 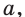 то в моменты времени
то в моменты времени  масса будет равной соответственно
масса будет равной соответственно 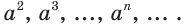 Поэтому естественно считать, что в любой момент времени
Поэтому естественно считать, что в любой момент времени 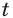 масса будет равной
масса будет равной 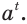 Можно проверить (сделайте это самостоятельно), что значения функции
Можно проверить (сделайте это самостоятельно), что значения функции 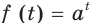 увеличиваются в одно и то же количество раз за равные промежутки времени.
увеличиваются в одно и то же количество раз за равные промежутки времени.
Таким образом, рассмотренный процесс описывают с помощью показательной функции 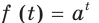 .
.
Из физики известно, что при радиоактивном распаде масса радиоактивного вещества за равные промежутки времени уменьшается в одно и то же количество раз.
Если поместить деньги в банк под определенный процент, то каждый год количество денег на счете будет увеличиваться в одно и то же количество раз.
Поэтому показательная функция описывает и эти процессы.
В таблице приведены свойства функции 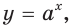 где
где 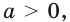
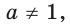 изученные в этом пункте.
изученные в этом пункте.
| Область определения | 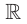 |
| Область значений | 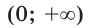 |
| Нули функции |  |
| Промежутки знакопостоянства | 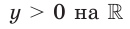 |
| Возрастание / убывание | Если 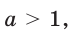 то функция возрастающая; если то функция возрастающая; если 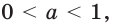 то функция убывающая то функция убывающая |
| Непрерывность | Непрерывная |
| Дифференцируемость | Дифференцируемая |
| Асимптоты | Если 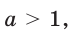 то график функции имеет горизонтальную асимптоту то график функции имеет горизонтальную асимптоту  при при 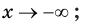 если если 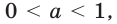 то график функции имеет горизонтальную асимптоту то график функции имеет горизонтальную асимптоту 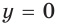 при при 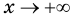 |
Пример №22
Найдите наименьшее и наибольшее значения функции 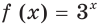 на отрезке
на отрезке 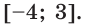
Решение:
Так как функция 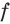 возрастает на отрезке
возрастает на отрезке 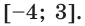 то наименьшее значение она принимает при
то наименьшее значение она принимает при 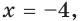 а наибольшее — при
а наибольшее — при 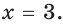
Следовательно,
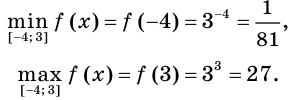
Ответ: 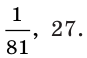
Пример №23
Решите уравнение 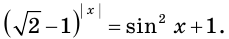
Решение:
Так как 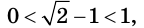 а
а 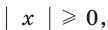 то
то 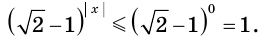 В то же время
В то же время 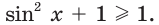 Таким образом, данное уравнение равносильно системе
Таким образом, данное уравнение равносильно системе
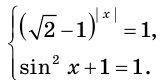
Отсюда 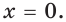
Ответ: 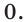
Вычисление показательных уравнений
Рассмотрим уравнения 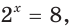
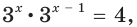
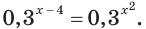
Во всех этих уравнениях переменная содержится только в показателе степени. Данные уравнения — примеры показательных уравнений.
Теорема 17.1. При 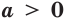 и
и 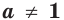 равенство
равенство 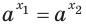 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 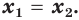
Доказательство. Очевидно, что если 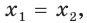 то
то 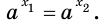
Докажем, что из равенства 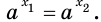 следует равенство
следует равенство 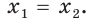 Предположим, что
Предположим, что 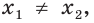 то есть
то есть 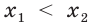 или
или 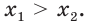 Пусть, например,
Пусть, например, 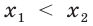 .
.
Рассмотрим показательную функцию 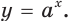 Она является либо возрастающей, либо убывающей. Тогда из неравенства
Она является либо возрастающей, либо убывающей. Тогда из неравенства 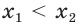 следует, что
следует, что 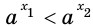 (при
(при 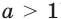 ) или
) или 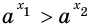 (при
(при 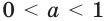 ). Однако по условию выполняется равенство
). Однако по условию выполняется равенство 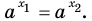 Получили противоречие.
Получили противоречие.
Аналогично рассматривают случай, когда 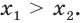
Следствие. Если 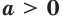 и
и 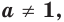 то уравнение
то уравнение

равносильно уравнению

Доказательство. Пусть 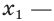 корень уравнения (1), то есть
корень уравнения (1), то есть 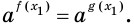 Тогда по теореме 17.1 получаем, что
Тогда по теореме 17.1 получаем, что 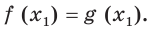 Следовательно,
Следовательно, 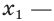 корень уравнения (2).
корень уравнения (2).
Пусть 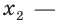 корень уравнения (2), то есть
корень уравнения (2), то есть 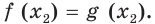 Отсюда
Отсюда 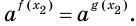
Мы показали, что каждый корень уравнения (1) является корнем уравнения (2) и наоборот, каждый корень уравнения (2) является корнем уравнения (1). Следовательно, уравнения (1) и (2) равносильны. А
Рассмотрим примеры решения показательных уравнений.
Пример №24
Решите уравнение 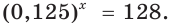
Решение:
Представим каждую из частей уравнения в виде степени с основанием 2. Имеем: 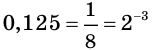 и
и 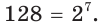 Запишем:
Запишем: 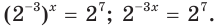 Это уравнение равносильно уравнению
Это уравнение равносильно уравнению
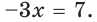
Отсюда 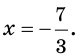 Ответ:
Ответ: 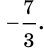
Пример №25
Решите уравнение 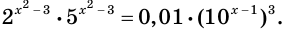
Решение:
Воспользовавшись свойствами степени, представим каждую из частей уравнения в виде степени с основанием 10. Имеем:
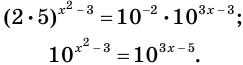
Переходим к равносильному уравнению:
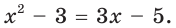
Отсюда 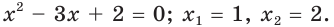
Ответ: 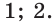
Пример №26
Решите уравнение 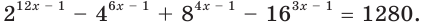
Решение:
Имеем:
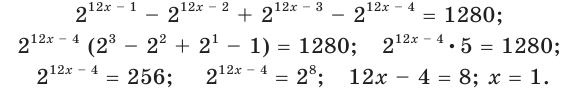
Ответ: 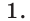
Пример №27
Решите уравнение 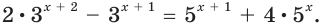
Решение:
Имеем:
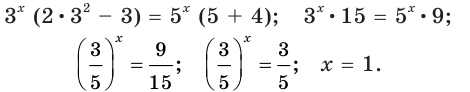
Ответ: 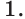
Пример №28
Решите уравнение 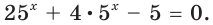
Решение:
Так как 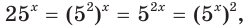 то данное уравнение удобно решать методом замены переменной.
то данное уравнение удобно решать методом замены переменной.
Пусть 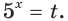 Тогда данное уравнение можно переписать так:
Тогда данное уравнение можно переписать так: 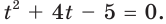 Отсюда
Отсюда 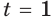 или
или 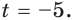 Если
Если 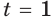 , то
, то 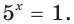 Отсюда
Отсюда 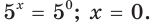 Если
Если 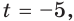 то
то 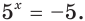 Так как
Так как 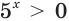 при любом
при любом 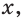 то уравнение
то уравнение 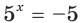 не имеет корней. Ответ:
не имеет корней. Ответ: 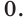
Пример №29
Решите уравнение 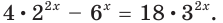
Решение:
Имеем: 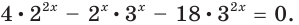
Так как 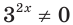 при любом
при любом 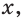 то, разделив обе части уравнения на
то, разделив обе части уравнения на 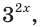 получим уравнение, равносильное данному:
получим уравнение, равносильное данному:
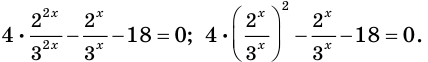
Пусть 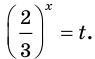 Тогда можно записать:
Тогда можно записать: 
Отсюда 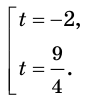 Имеем:
Имеем: 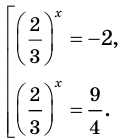
Так как 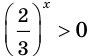 при любом
при любом  то первое уравнение совокупности решений не имеет. Второе уравнение совокупности перепишем так:
то первое уравнение совокупности решений не имеет. Второе уравнение совокупности перепишем так: 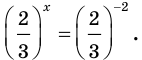
Отсюда 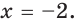
Ответ: 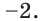
Пример №30
Решите уравнение 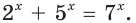
Решение:
Очевидно, что 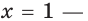 корень данного уравнения. Покажем, что этот корень — единственный.
корень данного уравнения. Покажем, что этот корень — единственный.
Разделив обе части исходного уравнения на 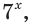 получим:
получим: 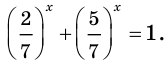
Рассмотрим функцию 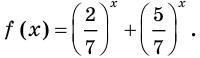 Так как функции
Так как функции 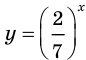 и
и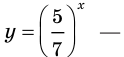 убывающие, то функция
убывающие, то функция 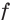 также является убывающей, а следовательно, каждое свое значение она принимает только один раз. Поэтому уравнение
также является убывающей, а следовательно, каждое свое значение она принимает только один раз. Поэтому уравнение 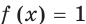 имеет единственный корень.
имеет единственный корень.
Ответ: 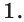
Пример №31
При каких значениях параметра 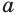 уравнение
уравнение
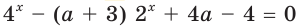 имеет единственный корень?
имеет единственный корень?
Решение:
Пусть 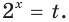 Имеем:
Имеем: 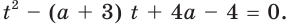
Отсюда 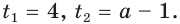 Следовательно, исходное уравнение равносильно совокупности:
Следовательно, исходное уравнение равносильно совокупности:
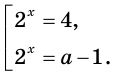
Первое уравнение совокупности имеет единственный корень 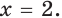 Второе уравнение совокупности при каждом значении параметра
Второе уравнение совокупности при каждом значении параметра 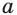 или имеет один корень, или вообще не имеет корней.
или имеет один корень, или вообще не имеет корней.
Для выполнения условия задачи второе уравнение совокупности либо должно не иметь корней, либо должно иметь единственный корень, равный 2.
Если 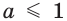 , то есть
, то есть 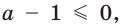 то уравнение
то уравнение 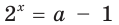 корней не имеет.
корней не имеет.
Число 2 является корнем второго уравнения совокупности, если 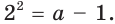 Отсюда
Отсюда 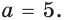
Ответ: 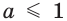 или
или 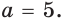
Вычисление показательных неравенств
Неравенства 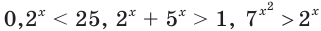 являются примерами показательных неравенств.
являются примерами показательных неравенств.
При решении многих показательных неравенств используют следующую теорему.
Теорема 18.1. При 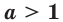 неравенство
неравенство 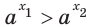 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 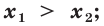 при
при 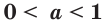 неравенство
неравенство 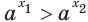 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 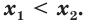
Справедливость этой теоремы следует из того, что при 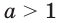 показательная функция
показательная функция 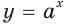 является возрастающей, а при
является возрастающей, а при 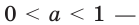 убывающей.
убывающей.
Следствие. Если 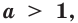 то неравенство
то неравенство 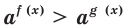 равносильно неравенству
равносильно неравенству 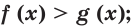 если
если 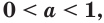 то неравенство
то неравенство 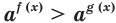 равносильно неравенству
равносильно неравенству 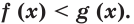
Воспользовавшись идеей доказательства следствия из теоремы 17.1, докажите это следствие самостоятельно.
Рассмотрим примеры решения показательных неравенств.
Пример №32
Решите неравенство 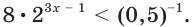
Решение:
Имеем: 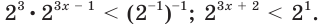
Так как основание степеней 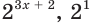 больше единицы, то последнее неравенство равносильно такому:
больше единицы, то последнее неравенство равносильно такому: 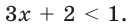
Отсюда 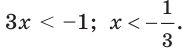
Ответ: 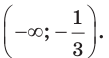
Пример №33
Решите неравенство 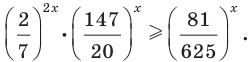
Решение:
Имеем: 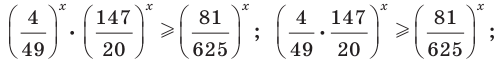
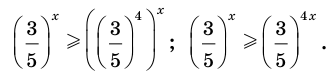
Так как 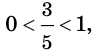 то последнее неравенство равносильно такому:
то последнее неравенство равносильно такому: 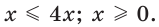
Ответ: 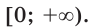
Пример №34
Решите неравенство 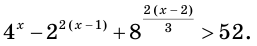
Решение:
Перепишем данное неравенство так: 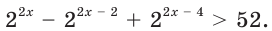
Отсюда
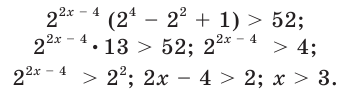
Ответ: 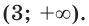
Пример №35
Решите неравенство 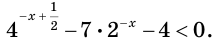
Решение.
Имеем:
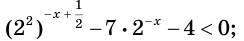
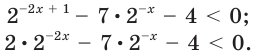
Пусть 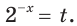 Тогда
Тогда 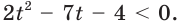
Решив это неравенство, получим 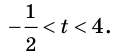 Отсюда
Отсюда 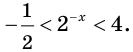
Так как 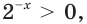 то
то 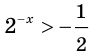 при всех
при всех 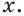 Поэтому достаточно решить неравенство
Поэтому достаточно решить неравенство 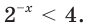
Имеем: 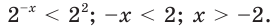
Ответ: 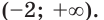
Пример №36
Решите неравенство 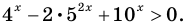
Решение:
Имеем: 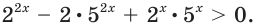 Так как
Так как 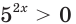 при любом
при любом 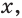 то, разделив обе части последнего неравенства на
то, разделив обе части последнего неравенства на 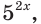 получаем равносильное неравенство
получаем равносильное неравенство 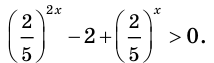
Пусть 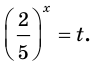 Тогда
Тогда 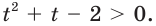 Решив это неравенство, получаем
Решив это неравенство, получаем 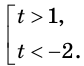
Отсюда: 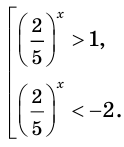
Из неравенства 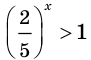 находим, что
находим, что 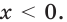 Неравенство
Неравенство 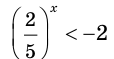 не имеет решений.
не имеет решений.
Ответ: 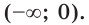
Пример №37
Решите неравенство 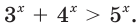
Решение:
Имеем: 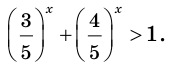
Рассмотрим функцию 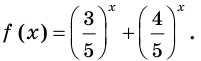 Заметим, что
Заметим, что 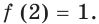 Так как функция
Так как функция  убывающая, то при
убывающая, то при 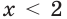 выполняется неравенство
выполняется неравенство 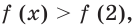 а при
а при 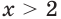 выполняется неравенство
выполняется неравенство 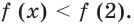 Следовательно, множеством решений неравенства
Следовательно, множеством решений неравенства  то есть неравенства
то есть неравенства 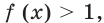 является промежуток
является промежуток 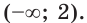
Свойство показательной функции
При условии, что 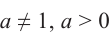
равенство 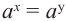 справедливо тогда и только тогда, если х = у. По данному свойству получаем:
справедливо тогда и только тогда, если х = у. По данному свойству получаем:
1)показательное уравнение 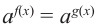 равносильно уравнению
равносильно уравнению 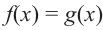 .
.
2)если в уравнении 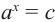 при
при 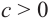 запишем
запишем 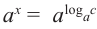 , то
, то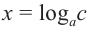 . Заданные показательные уравнения, при помощи определённых методов, приводятся к простейшим показательным уравнениям.
. Заданные показательные уравнения, при помощи определённых методов, приводятся к простейшим показательным уравнениям.
Применение свойств степени
Пример №38

Проверка.

Пример №39

Уравнения с разными основаниями можно решить разделив обе стороны на одну из степеней или логарифмированием обеих частей:
Примеры:

Введение новой переменной:
Пример:

Ответ: х = 2
Если уравнение состоит из членов, которые имеют одинаковую степень, а основания являются последовательными членами геометрической прогрессии, то обе части уравнения делится на один из крайних членов и вводится новая переменная.
Пример:

Зависимость между температурой и временем при охлаждении задаётся формулой Ньютона  где Т - температура в данный момент времени, То - температура в начальный момент времени, Тr - температура окружающей среды (средняя температура), r - скорость охлаждения ( скорость изменения за единицу времени),
где Т - температура в данный момент времени, То - температура в начальный момент времени, Тr - температура окружающей среды (средняя температура), r - скорость охлаждения ( скорость изменения за единицу времени),
t - время.
Решение показательных и логарифмических уравнений и неравенств
1. Конечная ОДЗ:
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Пример №40
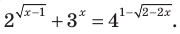
ОДЗ: 
Итак, ОДЗ: 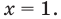
Проверка. 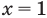 — корень
— корень 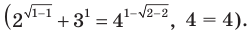 Других корней нет, поскольку в ОДЗ входит только одно число.
Других корней нет, поскольку в ОДЗ входит только одно число.
Ответ: 1.
2. Оценка значений левой и правой частей уравнения:
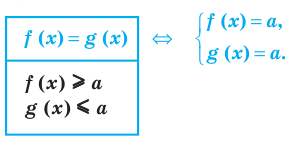
Если требуется решить уравнение вида 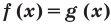 и выяснилось, что
и выяснилось, что 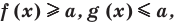 то равенство между левой и правой частями возможно тогда и только тогда, когда
то равенство между левой и правой частями возможно тогда и только тогда, когда 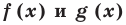 одновременно будут равны
одновременно будут равны 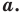
Пример №41
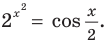
Оценим значения левой и правой частей данного уравнения: 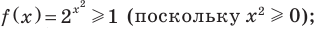 если
если 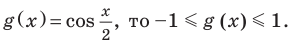 Итак,
Итак, 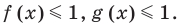 Тогда данное уравнение равносильно системе
Тогда данное уравнение равносильно системе 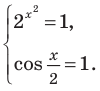
Из первого уравнения получаем 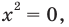 то есть
то есть 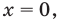 что удовлетворяет и второму уравнению.
что удовлетворяет и второму уравнению.
Ответ: 0.
3. Использование монотонности функций
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку значений левой и правой частей уравнения).
Теоремы о корнях уравнения:
1. Если в уравнении 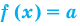 функция
функция 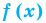 возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
Пример №42
Уравнение 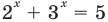 имеет единственный корень
имеет единственный корень 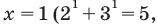 то есть
то есть 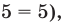 поскольку функция
поскольку функция 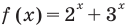 возрастает (на всей области определения
возрастает (на всей области определения 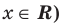 как сумма двух возрастающих функций.
как сумма двух возрастающих функций.
2. Если в уравнении  функция
функция  возрастает на некотором промежутке, а функция
возрастает на некотором промежутке, а функция  убывает на этом же промежутке (или наоборот), то это урав# нение может иметь не более чем один корень на этом промежутке.
убывает на этом же промежутке (или наоборот), то это урав# нение может иметь не более чем один корень на этом промежутке.
Пример:
Уравнение 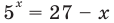 имеет единственный корень
имеет единственный корень 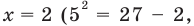 то есть
то есть 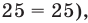 поскольку
поскольку 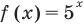 возрастает, а
возрастает, а 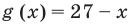 убывает (при всех
убывает (при всех 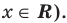
4. «Ищи квадратный трехчлен»
Попытайтесь рассмотреть заданное уравнение как квадратное относи# тельно некоторой переменной (или относительно некоторой функции).
Пример:
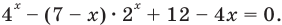
Запишем 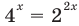 и введем замену
и введем замену 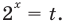
Получаем 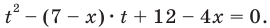 Рассмотрим это уравнение как квадратное относительно
Рассмотрим это уравнение как квадратное относительно 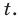 Его дискриминант
Его дискриминант 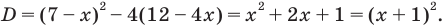 Тогда
Тогда 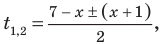 то есть
то есть 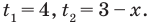 Обратная замена дает
Обратная замена дает 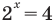 (отсюда
(отсюда 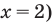 или
или 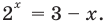 Последнее уравнение имеет единственный корень
Последнее уравнение имеет единственный корень 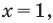 так как
так как 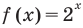 возрастает, а
возрастает, а 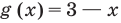 убывает (при всех
убывает (при всех 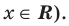
Ответ: 1; 2.
Пример №43
Решите уравнение 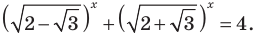
Решение:
Если 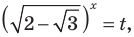 то
то 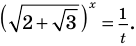 Получаем
Получаем 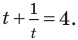 Отсюда
Отсюда 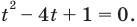 Тогда
Тогда 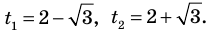 Обратная замена дает
Обратная замена дает 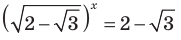 (отсюда
(отсюда 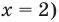 или
или 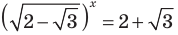 (отсюда
(отсюда 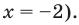
Ответ: 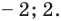
Комментарий:
Замечаем, что 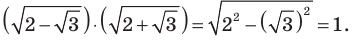 Таким образом, если
Таким образом, если 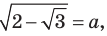 то
то 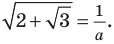 То есть данное уравнение имеет вид
То есть данное уравнение имеет вид 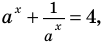 и его можно решить с помощью замены
и его можно решить с помощью замены 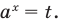 Но теперь эту замену можно непосредственно применить для данного уравнения, не вводя промежуточные обозначения. После обратной замены учитываем, что
Но теперь эту замену можно непосредственно применить для данного уравнения, не вводя промежуточные обозначения. После обратной замены учитываем, что
Пример №44
Решите уравнение 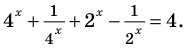
Комментарий:
Если привести все степени к одному основанию 2 и обозначить  то получим уравнение (1) (см. решение), в котором можно ввести замену
то получим уравнение (1) (см. решение), в котором можно ввести замену 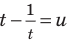 (тогда
(тогда 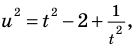 отсюда
отсюда 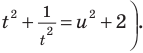 На ОДЗ данного уравнения
На ОДЗ данного уравнения  все замены и обратные замены являются равносильными преобразованиями этого уравнения. Таким образом, решив уравнения, полученные в результате замен, и выполнив обратные замены, мы получим корни данного уравнения.
все замены и обратные замены являются равносильными преобразованиями этого уравнения. Таким образом, решив уравнения, полученные в результате замен, и выполнив обратные замены, мы получим корни данного уравнения.
Решение:
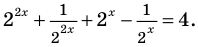
Замена 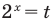 дает уравнение
дает уравнение
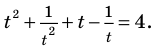
Обозначим 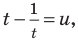 тогда
тогда 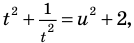 таким образом, из уравнения (1) получаем уравнение
таким образом, из уравнения (1) получаем уравнение 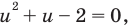 которое имеет корни:
которое имеет корни: 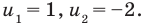
Обратная замена дает 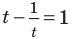 или
или 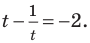
Тогда 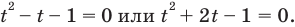
Получаем 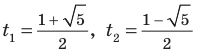 или
или 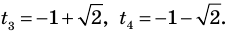 Тогда
Тогда 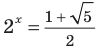 ( отсюда
( отсюда 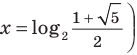 или
или 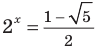 (корней нет, поскольку
(корней нет, поскольку 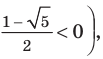 или
или 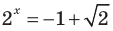 (отсюда
(отсюда 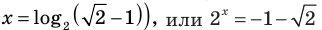 (корней нет, поскольку
(корней нет, поскольку 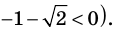
Ответ: 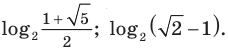
Пример №45
Решите уравнение 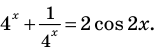
I способ
Комментарий:
Учитывая, что 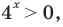 получаем, что в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. (Действительно, если
получаем, что в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. (Действительно, если 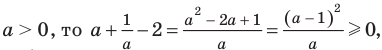 таким образом, при всех
таким образом, при всех 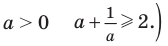
Для оценки значений правой части достаточно вспомнить, что областью значений функции 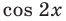 является промежуток
является промежуток 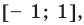 таким образом,
таким образом, 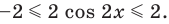
Решение:
Оценим значения левой и правой частей уравнения, 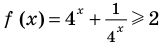 как сумма двух взаимно обратных положительных чисел. Если
как сумма двух взаимно обратных положительных чисел. Если 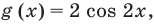 то
то 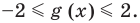 Таким образом,
Таким образом, 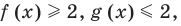 тогда данное уравнение равносильно системе
тогда данное уравнение равносильно системе 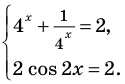
Из первого уравнения, используя замену 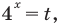 получаем
получаем
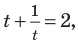 то есть
то есть 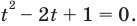 Отсюда
Отсюда 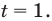
Тогда 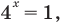 отсюда
отсюда 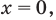 что удовлетворяет и второму уравнению.
что удовлетворяет и второму уравнению.
Ответ: 0.
II способ решения уравнения 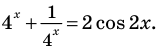
Комментарий:
Если обозначить 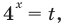 то данное уравнение приводится к уравнению (2) (см. решение), которое можно рассматривать как квадратное относительно переменной
то данное уравнение приводится к уравнению (2) (см. решение), которое можно рассматривать как квадратное относительно переменной 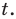 Заметим, что
Заметим, что 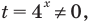 поэтому при таких значениях
поэтому при таких значениях 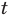 уравнения (1) и (2) являются равносильными. Далее используем условие существования корней квадратного уравнения.
уравнения (1) и (2) являются равносильными. Далее используем условие существования корней квадратного уравнения.
Решение:
После замены 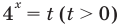 из данного уравнения получаем равносильное уравнение
из данного уравнения получаем равносильное уравнение 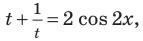 которое, в свою очередь, равносильно уравнению
которое, в свою очередь, равносильно уравнению 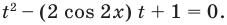
Рассмотрим уравнение (2) как квадратное относительно переменной 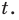 Тогда его дискриминант
Тогда его дискриминант 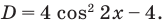
Уравнение (2) может иметь корни только тогда, когда 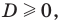 то есть когда
то есть когда 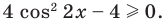 Отсюда
Отсюда 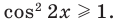
У этого неравенства знак «больше» не может выполняться 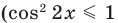 всегда), таким образом, неравенство (3) равносильно уравнению
всегда), таким образом, неравенство (3) равносильно уравнению 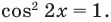 Тогда
Тогда 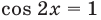 или
или 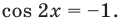 Подставляя эти значения в уравнение (2), получаем две системы:
Подставляя эти значения в уравнение (2), получаем две системы: 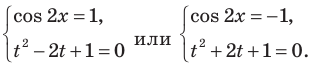 Во второй системе из второго уравнения имеем
Во второй системе из второго уравнения имеем 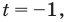 что не удовлетворяет условию
что не удовлетворяет условию 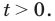 Таким образом, данное уравнение равносильно только первой системе. Из второго уравнения первой системы имеем
Таким образом, данное уравнение равносильно только первой системе. Из второго уравнения первой системы имеем 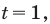 тогда
тогда 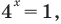 то есть
то есть 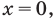 что удовлетворяет и первому уравнению этой системы.
что удовлетворяет и первому уравнению этой системы.
Ответ: 0.
Пример №46
Решите уравнение 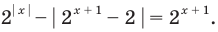
Комментарий:
Для решения уравнения с несколькими модулями можем применить общую схему (с. 240):
- найти ОДЗ;
- найти нули всех подмодульных функций;
- отметить нули на ОДЗ и разбить ОДЗ на промежутки;
- найти решения уравнения в каждом из промежутков.
Решение:
ОДЗ: 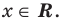
Нули подмодульных функций: 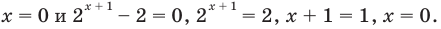
Этот нуль 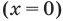 разбивает ОДЗ на два промежутка, в каждом из которых каждая подмодульная функция имеет постоянный знак (см. рисунок).
разбивает ОДЗ на два промежутка, в каждом из которых каждая подмодульная функция имеет постоянный знак (см. рисунок).
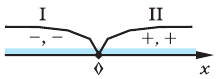
Промежуток I. При 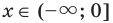 имеем уравнение
имеем уравнение 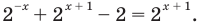 Тогда
Тогда
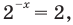 таким образом,
таким образом, 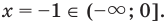
Промежуток II. При 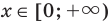 имеем уравнение
имеем уравнение 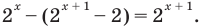 Тогда
Тогда
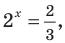 отсюда
отсюда 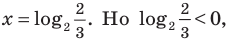 таким образом, во II промежутке данное уравнение корней не имеет.
таким образом, во II промежутке данное уравнение корней не имеет.
Пример №47
Решите уравнение
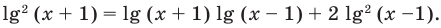
Решение:
ОДЗ 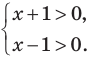 То есть
То есть 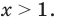
Поскольку 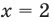 не является корнем данного уравнения, то при делении обеих частей уравнения на
не является корнем данного уравнения, то при делении обеих частей уравнения на 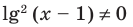 получаем равносильное (на ОДЗ) уравнение
получаем равносильное (на ОДЗ) уравнение
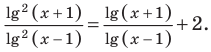
После замены 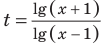 имеем уравнение
имеем уравнение 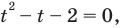 корни которого:
корни которого: 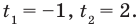 Выполнив обратную замену, получаем
Выполнив обратную замену, получаем
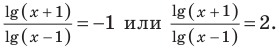
Тогда на ОДЗ имеем равносильные уравнения:
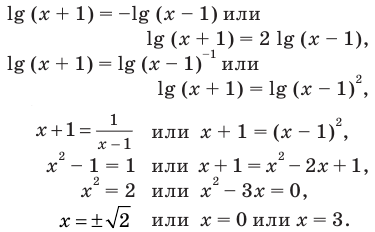
Учитывая ОДЗ, получаем
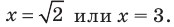
Ответ: 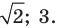
Комментарий:
Если выполнить замену 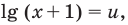
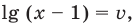 то получим уравнение
то получим уравнение 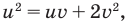 все члены которого имеют одинаковую суммарную степень — два. Напомним, что такое уравнение называется однородным и решается делением обеих частей на наибольшую степень одной из переменных. Разделим, например, обе части на
все члены которого имеют одинаковую суммарную степень — два. Напомним, что такое уравнение называется однородным и решается делением обеих частей на наибольшую степень одной из переменных. Разделим, например, обе части на 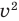 (то есть на
(то есть на 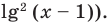
Чтобы не потерять корни уравнения при делении на выражение с переменной, необходимо те значения переменной, при которых это выражение равно нулю, рассмотреть отдельно. Значение 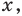 при котором
при котором 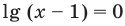 (тогда
(тогда 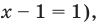 то есть
то есть 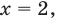 подставляем в данное уравнение.
подставляем в данное уравнение.
Для реализации полученного плана решения не обязательно вводить переменные 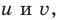 достаточно заметить, что данное уравнение однородное, разделить обе части на
достаточно заметить, что данное уравнение однородное, разделить обе части на 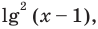 а затем ввести новую переменную
а затем ввести новую переменную 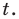
В конце учитываем, что все преобразования были равносильными на ОДЗ, следовательно, необходимо выбирать только те из найденных корней, которые входят в ОДЗ.
Пример №48
Решите уравнение 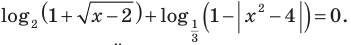
Комментарий:
Логарифмические функции, стоящие в левой части данного уравнения, принимают только неотрицательные значения.
Действительно, на всей области определения 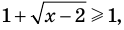 таким образом,
таким образом,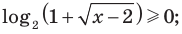 аналогично, поскольку
аналогично, поскольку 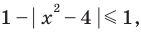 то на своей области определения
то на своей области определения 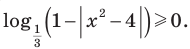 В этом случае сумма двух неотрицательных функций может равняться нулю тогда и только тогда, когда каждая из этих функций равна нулю.
В этом случае сумма двух неотрицательных функций может равняться нулю тогда и только тогда, когда каждая из этих функций равна нулю.
Заметим, что при переходе от данного уравнения к системе уравнений ОДЗ не изменяется, таким образом, ее можно не записывать в явном виде. При решении полученных простейших логарифмических уравнений ОДЗ также учитывается автоматически, поэтому ее можно вообще не записывать в решение.
Решение:
Поскольку на всей области определения 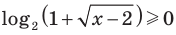 и
и 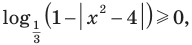 то данное уравнение равносильно системе
то данное уравнение равносильно системе
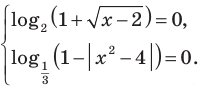
Из первого уравнения системы получаем 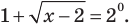 Тогда
Тогда 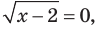 то есть
то есть 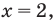 что удовлетворяет и второму уравнению системы.
что удовлетворяет и второму уравнению системы.
Ответ: 2.
Пример №49
При каких значениях параметра 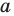 неравенство
неравенство 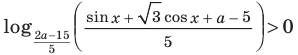 выполняется для любых значений
выполняется для любых значений 
Комментарий:
Сначала воспользуемся формулой 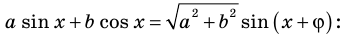
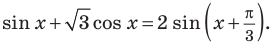 Далее запишем правую часть неравенства как значение логарифмической функции и, переходя к аргументу, учтем, что в случае, когда основание этой функции больше 1, функция возрастает, а когда меньше 1 (но больше 0) — убывает.
Далее запишем правую часть неравенства как значение логарифмической функции и, переходя к аргументу, учтем, что в случае, когда основание этой функции больше 1, функция возрастает, а когда меньше 1 (но больше 0) — убывает.
При дальнейшем анализе полученных неравенств учитываем, что неравенство 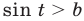 выполняется для любых значений
выполняется для любых значений 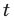 тогда и только тогда, когда
тогда и только тогда, когда 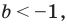 а неравенство
а неравенство 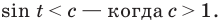
Решение:
Данное неравенство равносильно неравенству
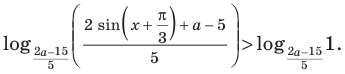
Эта неравенство равносильно совокупности систем
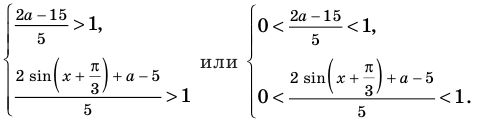 Тогда
Тогда 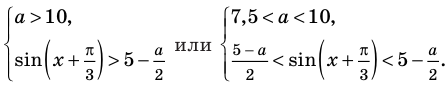
Неравенство с переменной 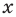 в последней совокупности систем будут выполняться для любых значений
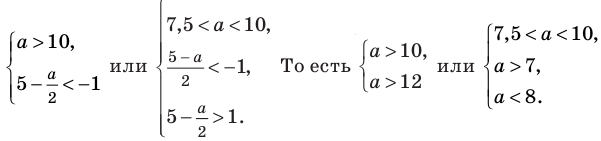
в последней совокупности систем будут выполняться для любых значений 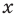 при условии:
при условии:
Тогда 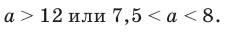
Ответ: при 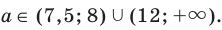
Пример №50
При каких значениях параметра а уравнение log2 (4' имеет единственный корень?
Комментарий:
Выполняя равносильные преобразования данного уравнения, учитываем, что при использовании определения логарифма для решения этого простейшего логарифмического уравнения его ОДЗ учитывается автоматически.
При выполнении замены переменной в задании с параметром учитываем, что после замены требование задачи может измениться.
Исследуя расположение корней квадратного трехчлена 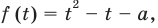 применим условия, приведенные на с. 225 в таблице 37 (для записи соответствующих условий используем обозначение:
применим условия, приведенные на с. 225 в таблице 37 (для записи соответствующих условий используем обозначение: 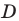 — дискриминант,
— дискриминант, 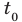 — абсцисса вершины параболы). Как известно, для того чтобы корни квадратного трехчлена
— абсцисса вершины параболы). Как известно, для того чтобы корни квадратного трехчлена 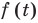 (с положительным коэффициентом при
(с положительным коэффициентом при 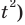 были расположены по разные стороны от числа
были расположены по разные стороны от числа 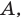 необходимо и достаточно, чтобы выполнялось условие
необходимо и достаточно, чтобы выполнялось условие 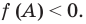
Решение:
Данное уравнение равносильно уравнению
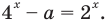
То есть 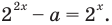 Замена
Замена 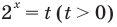 дает уравнение
дает уравнение
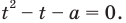
Требование задачи будет выполняться тогда и только тогда, когда уравнение (2) будет иметь единственный положительный корень. Это будет в одном из двух случаев:
- уравнение (2) имеет единственный корень, и он положительный;
- уравнение (2) имеет два корня, из которых только один положительный, а второй — отрицательный или нуль.
Для первого случая получаем 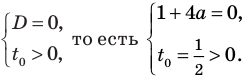
Таким образом, 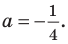
Для второго случая значение 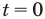 исследуем отдельно. При
исследуем отдельно. При 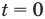 из уравнения (2) получаем
из уравнения (2) получаем 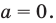 При
При 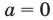 уравнение (2) имеет корни
уравнение (2) имеет корни 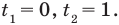 Таким образом, условие задачи при
Таким образом, условие задачи при 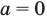 выполняется.
выполняется.
Остается еще один случай — корни уравнения (2) имеют разные знаки (расположены по разные стороны от нуля). Это будет тогда и только тогда, когда будет выполняться условие 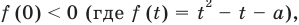 то есть условие
то есть условие 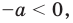 тогда
тогда 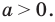 Объединяя все результаты, получаем ответ.
Объединяя все результаты, получаем ответ.
Ответ: при 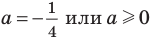 данное уравнение имеет единственный корень.
данное уравнение имеет единственный корень.
Справочный материал
Формулы сокращенного умножения. Разложение алгебраических выражений на множители
Основные приемы разложения многочлена на множители
Вынесение общего множителя за скобки 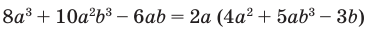
Способ группировки 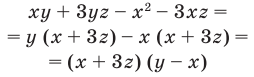
Применение формул сокращенного умножения 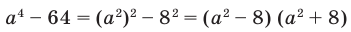
Разложение на множители квадратного трехчлена 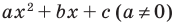
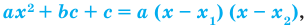
где 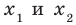 — корни квадратного трехчлена, то есть корни уравнения
— корни квадратного трехчлена, то есть корни уравнения 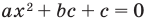
Поскольку 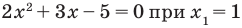 и
и 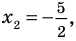 то
то 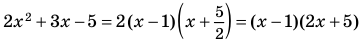
Обобщение некоторых формул сокращенного умножения
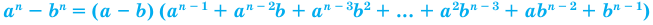
Примеры:
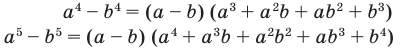
При 
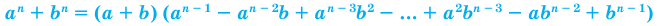
Примеры:
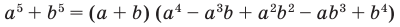
При 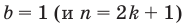
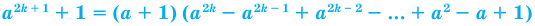
Системы уравнений
Если ставится задача найти все общие решения двух (или больше) уравнений с одной или несколькими переменными, то говорят, что требуется решить систему уравнений. Записывают систему уравнений, объединяя их фигурной скобкой. Решением системы называется такое значение переменной или такой упорядоченный набор значений переменных (если переменных несколько), которые удовлетворяют всем уравнениям системы. Решить систему уравнений — значит найти все ее решения или доказать, что решений нет. Если система не имеет решения, то ее называют несовместной.
Примеры:
1)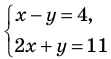 — система двух уравнений с двумя переменными. Пара чисел (5; 1), то есть
— система двух уравнений с двумя переменными. Пара чисел (5; 1), то есть 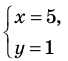 — решение системы.
— решение системы.
2) 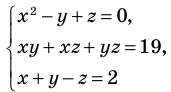 система трех уравнений с тремя переменными. Тройка
система трех уравнений с тремя переменными. Тройка 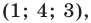 то есть
то есть 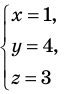 — одно из решений системы.
— одно из решений системы.
Равносильность систем уравнений:
Две системы уравнений называются равносильными на некотором множестве, если на этом множестве они имеют одинаковые решения (то есть каждое решение первой системы на этом множестве является решением второй и, наоборот, каждое решение второй системы является решением первой). Если изменить порядок уравнений заданной системы, то получим систему, равносильную заданной. Если одно из уравнений системы заменить на равносильное ему уравнение, то получим систему, равносильную заданной.
Областью допустимых значений (ОДЗ) системы называется общая область определения всех функций, входящих в запись этой системы. Все равносильные преобразования систем выполняются на ОДЗ исходной системы.
Основные способы решения систем уравнений
Способ подстановки:
Выражаем из одного уравнения системы одну переменную через другую (или через другие) и подставляем полученное выражение вместо соответствующей переменной во все другие уравнения системы (затем решаем полученное уравнение или систему и подставляем результат в выражение для первой переменной).
Пример №51
Решить систему 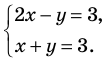
Решение:
Из первого уравнения системы 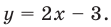 Подставляем во второе уравнение системы и получаем
Подставляем во второе уравнение системы и получаем 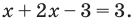 Отсюда
Отсюда 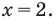 Тогда
Тогда 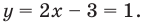
Ответ: (2; 1).
Способ сложения:
Если первое уравнение системы заменить суммой первого уравнения, умноженного на число 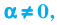 и второго уравнения, умноженного на число
и второго уравнения, умноженного на число  (а все остальные уравнения оставить без изменения), то получим систему, равносильную заданной.
(а все остальные уравнения оставить без изменения), то получим систему, равносильную заданной.
Пример №52
Решить систему 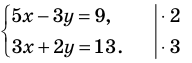
Решение:
Умножим обе части первого уравнения системы на 2, а второго — на 3 (чтобы получить как коэффициенты при переменной 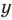 противоположные числа) и почленно сложим полученные уравнения. Из полученного уравнения находим значение
противоположные числа) и почленно сложим полученные уравнения. Из полученного уравнения находим значение 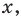 подставляем результат в любое уравнение системы и находим значение
подставляем результат в любое уравнение системы и находим значение 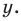
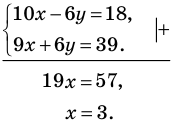
Тогда 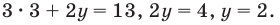
Ответ: (3; 2).
Основные способы решения систем уравнений
Способ подстановки:
Выполняем равносильные преобразования заданной системы так, чтобы удобно было строить графики всех уравнений, входящих в систему. Затем строим соответствующие графики и находим координаты точек пересечения построенных линий — эти координаты и являются решениями системы.
Пример №53
Решить графически систему 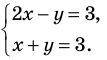
Решение:
Заданная система равносильна системе 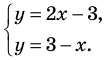
Графиком каждого из уравнений системы является прямая. Для построения прямой достаточно построить две ее точки. Например, для
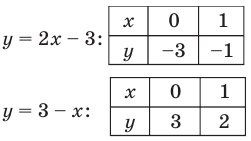
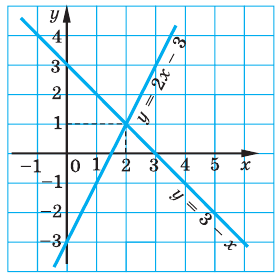
Графики пересекаются в единственной точке 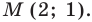 Итак, пара чисел (2; 1) — единственное решение заданной системы.
Итак, пара чисел (2; 1) — единственное решение заданной системы.
Ответ: (2; 1).
Пример №54
Решить графически систему 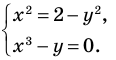
Решение:
Заданная система равносильна системе 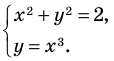
График первого уравнения — окружность радиуса 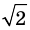 с центром в начале координат, а график второго — кубическая парабола
с центром в начале координат, а график второго — кубическая парабола 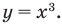 Эти два графика пересекаются в двух точках с координатами
Эти два графика пересекаются в двух точках с координатами 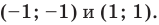
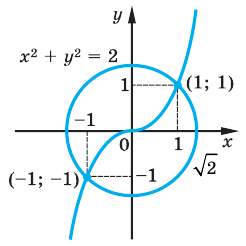
Ответ: 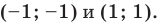 — решение системы.
— решение системы.
Квадратные неравенства
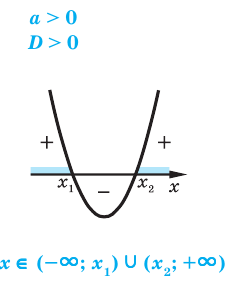
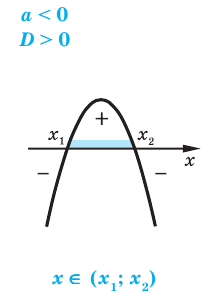
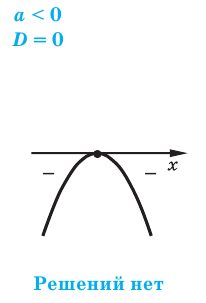
Квадратным неравенством называется неравенство вида 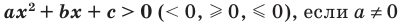
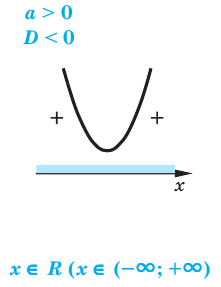
Для решения квадратного неравенства достаточно найти корни квадратного трехчлена 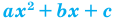 и построить эскиз его графика (параболу).
и построить эскиз его графика (параболу).
Как ответ записывают промежутки оси 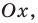 для которых точки параболы расположены выше оси
для которых точки параболы расположены выше оси 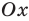 (для случая
(для случая 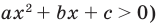 и ниже оси
и ниже оси 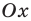 (для случая
(для случая 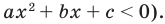
Если квадратный трехчлен имеет два разных корня 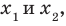 то для решения неравенства можно также использовать метод интервалов или равно% сильные преобразования неравенства.
то для решения неравенства можно также использовать метод интервалов или равно% сильные преобразования неравенства.
Разные случаи решения неравенства 
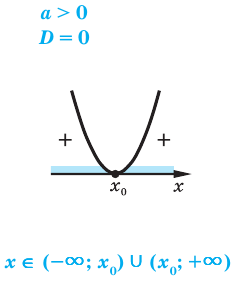
Пример №55
Решите неравенство 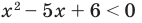
І способ
1. 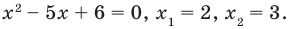
2. Строим эскиз графика функции 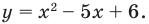
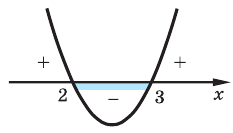
Ответ: (2 ; 3)
ІІ способ (метод интервалов)
Обозначим 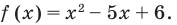
1. Область определения: 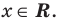
2. Нули функции: 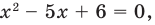
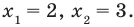
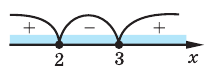
3. Отмечаем нули на области определения (на всей числовой прямой) и находим знак в каждом промежутке, на которые разбивается область определения (см. рисунок).
Для нахождения знаков функции 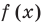 удобно разложить квадратный трехчлен на множители и записать заданное неравенство так:
удобно разложить квадратный трехчлен на множители и записать заданное неравенство так: 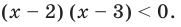
Ответ: (2; 3).
ІІІ способ (равносильные преобразования)
Поскольку 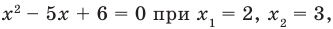 то заданное неравенство равносильно неравенству
то заданное неравенство равносильно неравенству 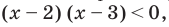 которое равносильно совокупности систем:
которое равносильно совокупности систем: 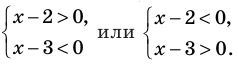
Тогда 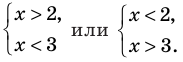
Из первой системы получаем 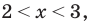 а вторая система не имеет решения.
а вторая система не имеет решения.
Ответ: (2; 3).
Нахождение области определения функции
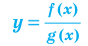
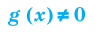 Знаменатель дроби не равен нулю
Знаменатель дроби не равен нулю
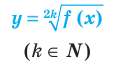
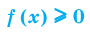 Под знаком корня четной степени может стоять только неотрицательное выражение
Под знаком корня четной степени может стоять только неотрицательное выражение
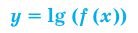
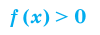 Под знаком логарифма может стоять только положительное выражение
Под знаком логарифма может стоять только положительное выражение
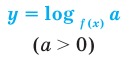
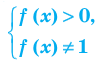 В основании логарифма может стоять только положительное выражение, не равное единице
В основании логарифма может стоять только положительное выражение, не равное единице
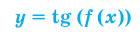
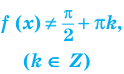 Под знаком тангенса может стоять только выражение, не равное
Под знаком тангенса может стоять только выражение, не равное 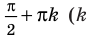 — целое)
— целое)
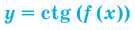
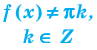 Под знаком котангенса может стоять только выражение, не равное
Под знаком котангенса может стоять только выражение, не равное 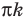
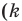 — целое)
— целое)

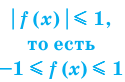 Под знаками арксинуса и арккосинуса может стоять только выражение, модуль которого меньше или равен единице
Под знаками арксинуса и арккосинуса может стоять только выражение, модуль которого меньше или равен единице

а) 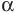 — натуральное
— натуральное  - любое число
- любое число
б) 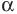 — целое отрицательное или нуль
— целое отрицательное или нуль 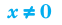
в) 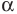 —нецелое положительное число
—нецелое положительное число 
г) 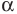 — нецелое отрицательное число
— нецелое отрицательное число 
Основные свойства числовых равенств и неравенств
Свойства числовых равенств:
1 Если 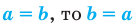
2. Если 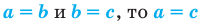 (транзитивность равенства)
(транзитивность равенства)
3. Если 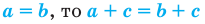
4. Если 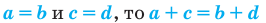
5. Если 
6. Если 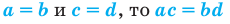
7. Если 
8. а) Если  то
то 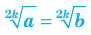
б) Если 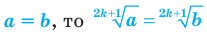
9. Если 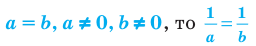
10. 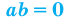 тогда и только тогда, когда
тогда и только тогда, когда 
11. 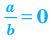 тогда и только тогда, когда
тогда и только тогда, когда 
Свойства числовых неравенств
1. Если 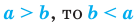
2. Если  (транзитивность неравенства)
(транзитивность неравенства)
3. Если 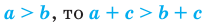
4. Если 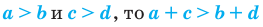
5. а) Если 
б) Если 
6. Если 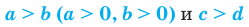
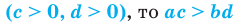
7. а) Если  то
то 
б) Если 
8. а) Если  то
то 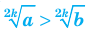
б) Если 
9. Если 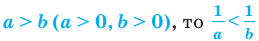
10. 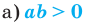 тогда и только тогда, когда
тогда и только тогда, когда  или
или 
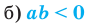 тогда и только тогда, когда
тогда и только тогда, когда  или
или 
11. а) 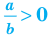 тогда и только тогда, когда
тогда и только тогда, когда  или
или 
б) 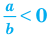 тогда и только тогда, когда
тогда и только тогда, когда  или
или 
Определение показательных уравнений и неравенств
Уравнение называется показательным, если его переменные входят только в показатели степеней.
Примеры:
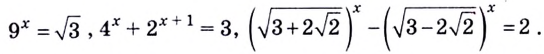
Существует много видов показательных уравнений и различных подходов к их решению. Основными методами решения показательных уравнений являются:
- Метод приведения обеих частей уравнения к степеням с одинаковыми основаниями.
- Метод введения новой переменной.
- Функционально-графический метод. Рассмотрим каждый из этих методов подробнее.
Метод приведения обеих частей уравнения к степеням с одинаковыми основаниями
Метод приведения обеих частей уравнения к степеням с одинаковыми основаниями применяется в двучленных уравнениях, которые можно свести к виду 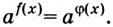 Такие уравнения решаются на основе монотонности показательной функции.
Такие уравнения решаются на основе монотонности показательной функции.
Если 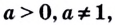 то уравнения
то уравнения 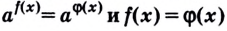 — равносильны.
— равносильны.
Пример №56
Решите уравнение: 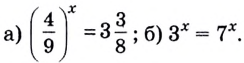
Решение:
а) Представим правую часть уравнения в виде неправильной дроби: 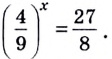
Запишем правую и левую части уравнения в виде степени с основанием 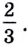 Получим:
Получим: 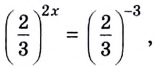 отсюда
отсюда 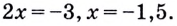
б) Поскольку 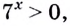 разделим обе части уравнения
разделим обе части уравнения 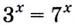 на
на 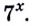 Получим
Получим 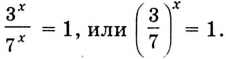 Запишем число 1 в виде степени с основанием
Запишем число 1 в виде степени с основанием 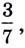 тогда
тогда 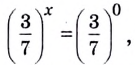 отсюда
отсюда 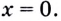
Существуют двучленные уравнения, члены которых вы пока не можете свести к степеням с одинаковыми основаниями. В общем виде их можно записать так: 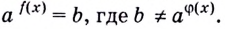
Если 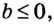 то уравнение решений не имеет, поскольку показательная функция принимает только положительные значения.
то уравнение решений не имеет, поскольку показательная функция принимает только положительные значения.
Если 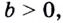 то уравнение имеет одно решение, поскольку прямая
то уравнение имеет одно решение, поскольку прямая 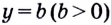 всегда пересекает график показательной функции. Как записать такое решение, например уравнения
всегда пересекает график показательной функции. Как записать такое решение, например уравнения 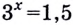 (рис. 26), вы узнаете позже.
(рис. 26), вы узнаете позже.
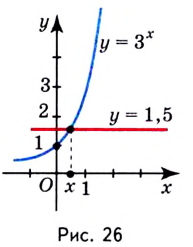
Методом введения новой переменной решаются многие виды уравнений
Рассмотрим решение некоторых из них на конкретных примерах.
Пример №57
Решите уравнение:
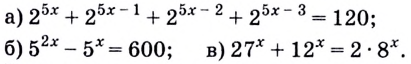
Решение:
В показателе каждой степени этого уравнения содержится одно и то же выражение 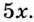 Обозначим наименьший показатель степени буквой
Обозначим наименьший показатель степени буквой 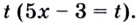 Тогда уравнение будет иметь вид:
Тогда уравнение будет иметь вид:
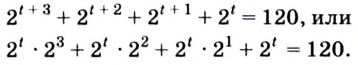
Вынесем общий множитель 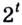 за скобки. Получим:
за скобки. Получим: 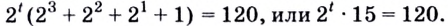 Отсюда
Отсюда 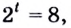 или
или 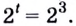 Следовательно,
Следовательно, 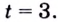 Поскольку
Поскольку 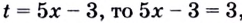 отсюда
отсюда 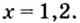
Решая такие уравнения, не обязательно вводить новую переменную, а можно сразу выносить общий множитель за скобки 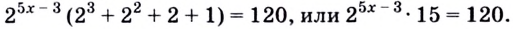 Отсюда
Отсюда 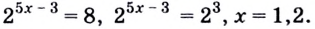
Именно поэтому этот способ называют способом вынесения общего множителя за скобки.
б) Пусть 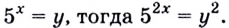 Подставим
Подставим 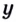 в данное уравнение. Имеем:
в данное уравнение. Имеем: 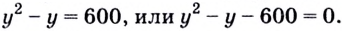 Корни последнего уравнения:
Корни последнего уравнения: 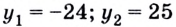 (проверьте).
(проверьте).
Поскольку 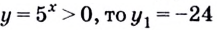 — посторонний корень. Если
— посторонний корень. Если 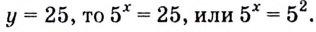
Следовательно, 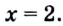
в) Запишем данное уравнение в виде 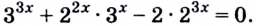
Разделим каждый член уравнения на 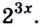 Получим:
Получим:
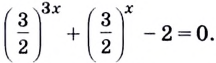 тогда
тогда 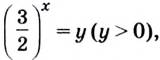 тогда
тогда 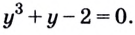
Поскольку 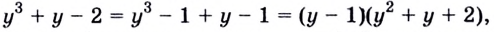 то уравнение
то уравнение 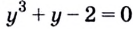 имеет один корень
имеет один корень 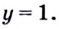 Следовательно,
Следовательно, 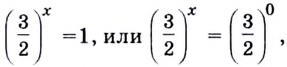 отсюда
отсюда 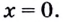
Функционально-графический метод
Функционально-графический метод состоит в следующем:
- с помощью построения графиков (или путём подбора) находят один корень уравнения;
- доказывают, что других корней уравнение не имеет.
Пример №58
Решите уравнение: 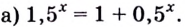
Решение:
Графически или методом проб убеждаемся, что 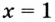 — корень уравнения. Поскольку
— корень уравнения. Поскольку 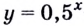 — возрастающая функция, так как
— возрастающая функция, так как 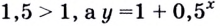 — убывающая
— убывающая  то других корней уравнение не имеет.
то других корней уравнение не имеет.
Если в показательном уравнении знак равенства изменить на знак неравенства, то получим показательное неравенство.
Неравенство называется показательным, если его переменные входят только в показатели степеней.
Для решения показательных неравенств используют те же методы, что и для решения показательных уравнений. А также правила решения простейших показательных неравенств, т.е. неравенств вида 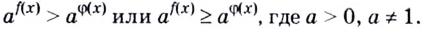
Решая простейшие показательные неравенства, используют монотонность (возрастание или убывание) показательной функции. А именно:
1. Если 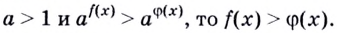
2. Если 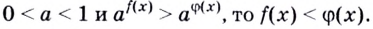
Пример №59
Решите неравенство:
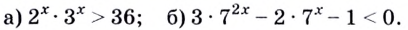
Решение:
а) Представим правую и левую части неравенства в виде степени с основанием 6:
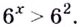
Поскольку 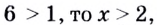 или
или 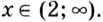
б) Пусть 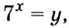 тогда
тогда 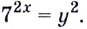 Подставим
Подставим 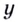 в данное неравенство. Получим:
в данное неравенство. Получим: 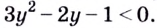 Поскольку квадратный трёхчлен
Поскольку квадратный трёхчлен 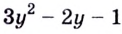 имеет корни
имеет корни 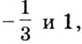 то множеством решений соответствующего неравенства будет:
то множеством решений соответствующего неравенства будет: 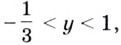 или
или 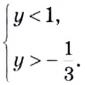
Поскольку 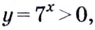 то условие
то условие 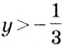 выполняется всегда. Если
выполняется всегда. Если 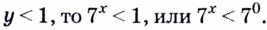 Следовательно,
Следовательно, 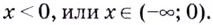 Показательные уравнения и неравенства — отдельный вид трансцендентных уравнений и неравенств. Вы уже знаете, что к трансцендентным относятся тригонометрические уравнения и неравенства. Трансцендентными считают также уравнения и неравенства, в которых сочетаются трансцендентные выражения с алгебраическими:
Показательные уравнения и неравенства — отдельный вид трансцендентных уравнений и неравенств. Вы уже знаете, что к трансцендентным относятся тригонометрические уравнения и неравенства. Трансцендентными считают также уравнения и неравенства, в которых сочетаются трансцендентные выражения с алгебраическими:
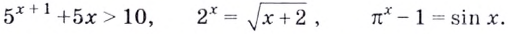
Только для некоторых из подобных уравнений можно указать точные решения. Их приближённые корни находят в основном графическим способом.
Уравнения вида 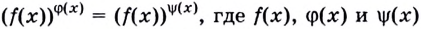 -функции переменной
-функции переменной 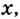 называются показательно-степенными.
называются показательно-степенными.
Их решают, проверяя, не будут ли решениями данного уравнения корни уравнений:
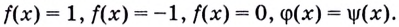
Полученные таким образом корни подлежат проверке.
Пример №60
Решите уравнение 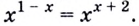
Решение:
1) Подставим 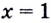 в данное уравнение. Имеем:
в данное уравнение. Имеем: 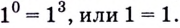 Следовательно,
Следовательно, 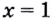 — корень данного уравнения.
— корень данного уравнения.
2) Если 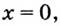 то имеем правильное равенство
то имеем правильное равенство 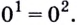 Следовательно,
Следовательно, 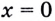 — корень данного уравнения.
— корень данного уравнения.
3) Если 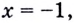 получим равенство
получим равенство 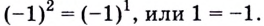 Равенство неправильное, следовательно,
Равенство неправильное, следовательно, 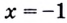 — посторонний корень.
— посторонний корень.
4) Решим уравнение 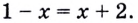
Его корень 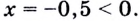 Это посторонний корень, так как
Это посторонний корень, так как 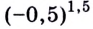 не существует.
не существует.
Ответ. 0; 1.
Пример №61
Решите уравнение 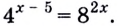
Решение:
Запишем правую и левую части как степени числа 2: 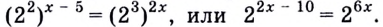 Отсюда
Отсюда 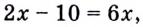
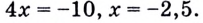
Пример №62
Решите неравенство 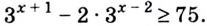
Решение:
Запишем неравенство в виде 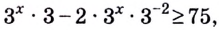 или
или 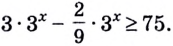 Вынесем
Вынесем 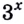 за скобки и упростим полученное неравенство
за скобки и упростим полученное неравенство 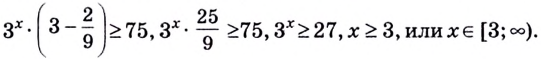
Пример №63
Решите уравнение 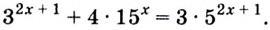
Решение:
Запишем уравнение в виде
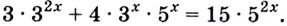
Разделим левую и правую части уравнения на 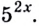 Имеем:
Имеем:
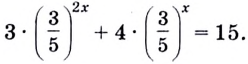
Обозначим 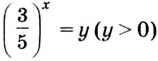 и подставим
и подставим 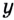 в данное уравнение.Получим:
в данное уравнение.Получим: 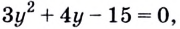 отсюда
отсюда 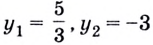 (посторонний корень).
(посторонний корень).
Пример №64
Решите уравнение 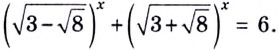
Решение:
Найдём произведение оснований степеней:
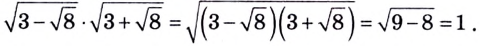
То есть 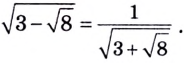
Обозначим 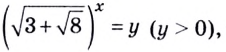 тогда
тогда 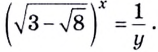
Перейдём к уравнению с переменной 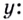
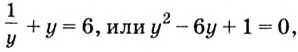 отсюда
отсюда 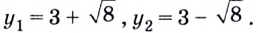
Получим:
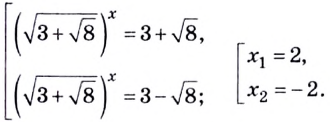
Пример №65
Решите графически неравенство 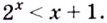
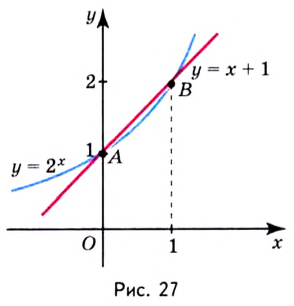
Решение:
Построим в одной системе координат графики функций 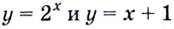 (рис. 27). Они пересекаются в точках
(рис. 27). Они пересекаются в точках 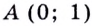 и
и 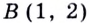 (проверьте подстановкой). Значения
(проверьте подстановкой). Значения 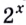 меньше соответствующих значений
меньше соответствующих значений 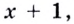 если
если 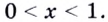
Ответ. 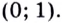
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Логарифмические уравнения и неравенства
- Степенная функция - определение и вычисление
- Степень с целым показателем
- Корень n-й степени
- Логарифмические выражения
- Показательная функция, её график и свойства
- Производные показательной и логарифмической функций
- Показательно-степенные уравнения и неравенства

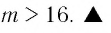
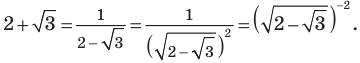
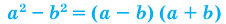
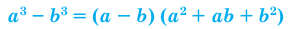
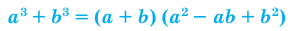
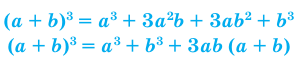
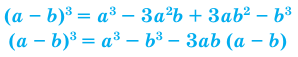
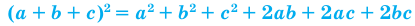
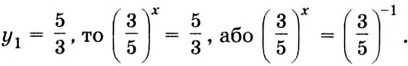 Следовательно,
Следовательно, 