
Показательно-степенные уравнения и неравенства с примерами решения
Содержание:
Показательно-степенные уравнения:
Показательно степенными уравнениями обычно называют уравнения, содержащие выражения вида 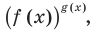
Основные способы решения уравнения вида 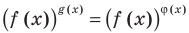
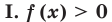
Ориентир
Используем (если возможно) основное логарифмическое тождество в виде
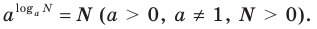
Логарифмируем (если возможно) обе части уравнения по числовому основанию или представляем все степени как степени с одним и тем же числовым основанием по формуле
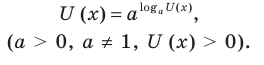
Пример:
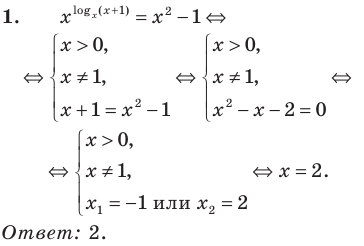
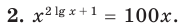
На ОДЗ (х > 0) обе части уравнения положительны, поэтому после логарифмирования по основанию 10 получаем уравнение, равносильное данному:
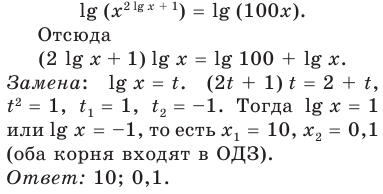
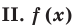 — произвольное выражение
— произвольное выражение
Ориентир:
Две степени с одинаковыми основаниям и 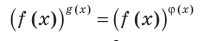 могут быть равными в одном из четырех случаев:
могут быть равными в одном из четырех случаев:
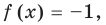 для корней, этого уравнения
для корней, этого уравнения 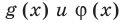 — целые, числа одинаковой четности;
— целые, числа одинаковой четности;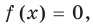 для корней этого уравнения
для корней этого уравнения 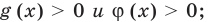
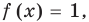 для корней этого уравнения
для корней этого уравнения 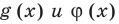 существуют;
существуют;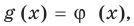 для корней этого уравнения существуют
для корней этого уравнения существуют 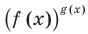 и
и 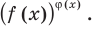
Пример:
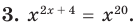
Если предположить, что основание степени 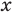 является числом, то сначала рассмотрим три особых случая (основание степени равно
является числом, то сначала рассмотрим три особых случая (основание степени равно 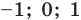 а затем приравняем показатели степеней:
а затем приравняем показатели степеней:
- при
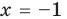 получаем верное равенство
получаем верное равенство 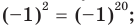
- при
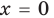 то
то 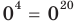 — верное равенство;
— верное равенство; - при
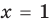 то
то 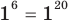 — верное равенство;
— верное равенство; - при
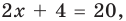 то есть
то есть 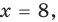 то
то 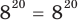 — верное равенство.
— верное равенство.
Ответ: 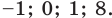
Замечание. Если предположить, что основание 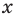 является переменной, то функция
является переменной, то функция 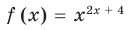 считается определенной только при
считается определенной только при 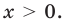 В этом случае данное уравнение имеет только корни 1 и 8, и получаем ответ:
В этом случае данное уравнение имеет только корни 1 и 8, и получаем ответ: 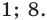
Таким образом, ответ к такому уравнению нельзя записать однозначно.
Объяснение и обоснование
Показательно степенными уравнениями и неравенствами обычно называют уравнения и неравенства, содержащие выражения вида 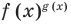 (в которых переменная входит и в основание, и в показатель степени).
(в которых переменная входит и в основание, и в показатель степени).
Анализируя показательно-степенные уравнения, представленные в табл. 26, следует помнить, что в школьном курсе математики понятие уравнения на разных этапах вводилось по-разному. В 4 -5 классах уравнением называлось числовое равенство, содержащее неизвестное число, обозначенное буквой. Значение неизвестного, при котором уравнение обращается в верное числовое равенство, называлось корнем, или решением этого уравнения. Например, для уравнения 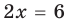 корнем является значение
корнем является значение 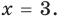
С точки зрения приведенного определения, в уравнении 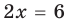 буквой
буквой 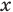 обозначено хотя и неизвестное нам, но конкретное число, поэтому
обозначено хотя и неизвестное нам, но конкретное число, поэтому 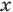 может принимать единственное значение
может принимать единственное значение 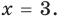 Но такое определение затрудняет в дальнейшем работу с уравнением. Когда
Но такое определение затрудняет в дальнейшем работу с уравнением. Когда 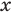 принимает единственное значение, мы не можем применять, например, графическое решение уравнения (имея только одно значение
принимает единственное значение, мы не можем применять, например, графическое решение уравнения (имея только одно значение 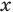 , невозможно получить график
, невозможно получить график 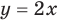 как прямую линию на плоскости). Поэтому, начиная с 6-7 классов, уравнение определяется как равенство с переменной (а корнем, или решением уравнения соответственно называется такое значение переменной, при котором это уравнение обращается в верное числовое равенство). Тогда
как прямую линию на плоскости). Поэтому, начиная с 6-7 классов, уравнение определяется как равенство с переменной (а корнем, или решением уравнения соответственно называется такое значение переменной, при котором это уравнение обращается в верное числовое равенство). Тогда 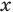 в уравнении
в уравнении 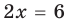 — это переменная, для которой нет ни одного ограничения, и поэтому
— это переменная, для которой нет ни одного ограничения, и поэтому 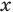 может быть любым числом (ОДЗ уравнения:
может быть любым числом (ОДЗ уравнения: 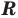 ). При таком подходе каждому значению переменной
). При таком подходе каждому значению переменной 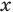 соответствует единственное значение переменной
соответствует единственное значение переменной 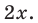 Таким образом, это уравнение можно решить графически, построив графики функций
Таким образом, это уравнение можно решить графически, построив графики функций 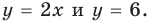 Кроме того, можно записать уравнение в общем виде как равенство
Кроме того, можно записать уравнение в общем виде как равенство 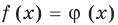 и обоснованно применить свойства функций для решения уравнений.
и обоснованно применить свойства функций для решения уравнений.
Для всех видов уравнений, которые рассматривались в курсе алгебры или алгебры и начал анализа, приведенные два определения уравнения приводят к одному и тому же результату при решении уравнений. Но в случае показательно-степенного уравнения иногда можно получить разные ответы, используя разные подходы к определению уравнения. Например, решим уравнение 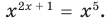
Если рассматривать такое уравнение как числовое равенство, то две степени с одинаковым основанием 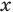 могут быть равными только в одном из четырех случаев. А именно: если основанием степени является одно из значений
могут быть равными только в одном из четырех случаев. А именно: если основанием степени является одно из значений 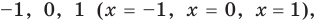 то степени могут быть равными даже тогда, когда их показатели будут разными (при условии, что эти степени существуют). Во всех остальных случаях степени с одинаковым основанием будут равными только тогда, когда показатели этих степеней будут равными (
то степени могут быть равными даже тогда, когда их показатели будут разными (при условии, что эти степени существуют). Во всех остальных случаях степени с одинаковым основанием будут равными только тогда, когда показатели этих степеней будут равными (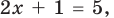 то есть
то есть 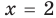 ). Следовательно, для получения всех корней данного уравнения достаточно проверить значения
). Следовательно, для получения всех корней данного уравнения достаточно проверить значения 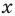 , равные
, равные 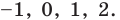 Все эти числа являются корнями, так как при подстановке каждого из них в данное уравнение оно обращается в верное числовое равенство.
Все эти числа являются корнями, так как при подстановке каждого из них в данное уравнение оно обращается в верное числовое равенство.
Если же рассматривать это уравнение как равенство с переменной и встать на функциональную точку зрения, то функция 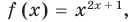 как правило, считается определенной только при
как правило, считается определенной только при 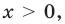 тогда данное уравнение имеет только два корня: 1 и 2.
тогда данное уравнение имеет только два корня: 1 и 2.
Таким образом, в рассмотренном уравнении ответ нельзя записать однозначно (поскольку каждый из указанных подходов к определению уравнения имеет право на существование и реально используется в математике). Поэтому в подобных ситуациях приходится приводить оба варианта ответа. Аналогичный пример приведен в табл. 26.
Обобщая приведенные выше рассуждения, заметим, что в том слу чае, когда при решении уравнения вида 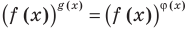 из условия не следует, что основание степени
из условия не следует, что основание степени 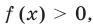 необходимо рассмотреть три особых случая: основание
необходимо рассмотреть три особых случая: основание 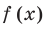 равно -1 , 0, 1 (при этом степени
равно -1 , 0, 1 (при этом степени 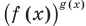 и
и 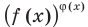 могут быть равными даже тогда, когда показатели
могут быть равными даже тогда, когда показатели 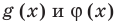 разные), а затем приравнять показатели
разные), а затем приравнять показатели 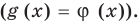 Если же из условия следует, что
Если же из условия следует, что 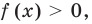 то рассматриваем только один особый случай — основание степени равно
то рассматриваем только один особый случай — основание степени равно 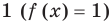 — и приравниваем показатели степеней
— и приравниваем показатели степеней 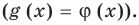
Например, решим уравнение 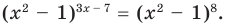
Из условия не следует, что основание степени 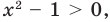 следовательно, приходится рассматривать все случаи.
следовательно, приходится рассматривать все случаи.
- 1) Если
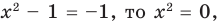 и тогда
и тогда 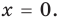 Подставляя это значение в данное уравнение, имеем
Подставляя это значение в данное уравнение, имеем 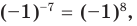 то есть
то есть 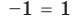 (неверное равенство). Таким образом,
(неверное равенство). Таким образом, 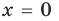 не является корнем данного уравнения.
не является корнем данного уравнения. - 2) Если
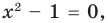 то есть
то есть 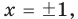 то при этих значениях
то при этих значениях 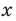 данное уравнение обращается в неверное числовое равенство (поскольку значения выражений
данное уравнение обращается в неверное числовое равенство (поскольку значения выражений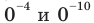 не существуют). Таким образом, числа 1 и -1 не являются корнями данного уравнения.
не существуют). Таким образом, числа 1 и -1 не являются корнями данного уравнения. - 3) Если
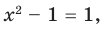 то есть
то есть 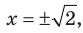 то данное уравнение обращается в верное равенство
то данное уравнение обращается в верное равенство 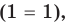 следовательно,
следовательно, 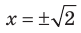 — корни данного уравнения.
— корни данного уравнения. - 4) Приравняем показатели степеней данного уравнения (основания степеней в левой и правой частях уравнения одинаковы):
 тогда
тогда 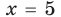 (при подстановке получаем верное равенство
(при подстановке получаем верное равенство 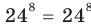 ).
).
Объединяя полученные результаты, получаем ответ.
Ответ: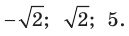
Замечание. При 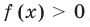 для решения уравнения
для решения уравнения 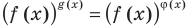 можно прологарифмировать обе его части по любому числовому основанию, получить равносильное уравнение, в котором уже не придется рассматривать особый случай — он будет учтен автоматически. Это связано с тем, что функция
можно прологарифмировать обе его части по любому числовому основанию, получить равносильное уравнение, в котором уже не придется рассматривать особый случай — он будет учтен автоматически. Это связано с тем, что функция 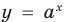 при
при 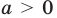 имеет особый случай, если
имеет особый случай, если 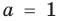 (см. график функции
(см. график функции 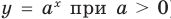 ), а функция
), а функция 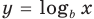 (где
(где 
 ) особых случаев не имеет.
) особых случаев не имеет.
Также отметим, что при решении неравенств вида 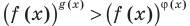 обычно используют функциональный подход и считают, что
обычно используют функциональный подход и считают, что 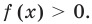 Когда в показательно-степенное уравнение входят выражения вида
Когда в показательно-степенное уравнение входят выражения вида 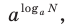 для его решения можно воспользоваться основным логарифмическим тождеством, В этом случае следует учитывать ОДЗ данного уравнения (см. пример 1 в табл. 26).
для его решения можно воспользоваться основным логарифмическим тождеством, В этом случае следует учитывать ОДЗ данного уравнения (см. пример 1 в табл. 26).
Достаточно часто при решении показательно-степенных уравнений логарифмируют обе его части. Это можно сделать только тогда, когда обе части уравнения положительны на его ОДЗ (см. пример 2 в табл. 26). Приведем еще несколько примеров решения показательно-степенных уравнений и неравенств.
Примеры с решениями
Пример №1
Решите уравнение 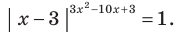
Решение:
Поскольку 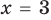 не является корнем данного уравнения (
не является корнем данного уравнения (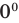 не существует), то при
не существует), то при 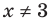 обе его части положительны. После логарифмирования (по основанию 10) обеих частей данного уравнения получаем равносильные ему уравнения:
обе его части положительны. После логарифмирования (по основанию 10) обеих частей данного уравнения получаем равносильные ему уравнения:
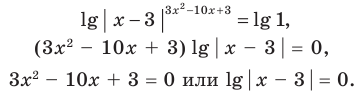
Из первого полученного уравнения имеем 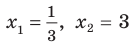 (не является корнем), а из второго —
(не является корнем), а из второго — 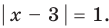 Тогда
Тогда 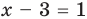 или
или 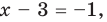 то есть
то есть 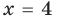 или
или 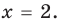 Ответ:
Ответ: 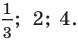
Комментарий:
Поскольку 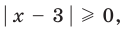 то из особых случаев можно рассмотреть только один — основание равно 0 (
то из особых случаев можно рассмотреть только один — основание равно 0 ( 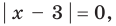 то есть
то есть 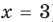 ). Чтобы не рассматривать случай, когда основание равно 1, достаточно при
). Чтобы не рассматривать случай, когда основание равно 1, достаточно при 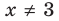 прологарифмировать обе части уравнения по числовому основанию (например, по основанию 10). При
прологарифмировать обе части уравнения по числовому основанию (например, по основанию 10). При 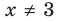 обе части данного уравнения положительны, поэтому после логарифмирования получаем уравнение, равносильное данному. Поскольку все дальнейшие преобразования равносильны (при
обе части данного уравнения положительны, поэтому после логарифмирования получаем уравнение, равносильное данному. Поскольку все дальнейшие преобразования равносильны (при 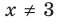 ), то все полученные решения (не равные 3) являются корнями данного уравнения.
), то все полученные решения (не равные 3) являются корнями данного уравнения.
Пример №2
Решите уравнение 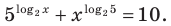
Комментарий:
Прологарифмировать обе части данного уравнения не удается (в левой части стоит сумма), поэтому попытаемся представить все степени в виде степеней с одним и тем же числовым основанием. Так как в уравнении есть логарифм по основанию 2, представим все данные степени в виде степеней с основанием 2 по формуле 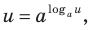 где
где 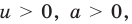
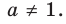 Тогда
Тогда
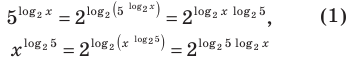
(то есть слагаемые, стоящие в левой части данного уравнения, одинаковы). После получения уравнения (2) (см. решение) можно использовать равенство (1) справа налево, а также записать правую часть уравнения (2) как степень числа 2 или прологарифмировать обе его части по основанию 2.
Решение:
ОДЗ: 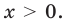 На этой ОДЗ данное уравнение равносильно уравнениям:
На этой ОДЗ данное уравнение равносильно уравнениям:
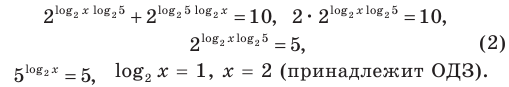
Ответ: 2.
Пример №3
Решите систему уравнений: 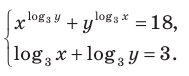
Комментарий :
Используем равносильные преобразования системы. Для этого учтем ОДЗ и проследим, чтобы на этой ОДЗ преобразования уравнений как в прямом, так и в обратном направлениях сохраняли верные равенства. В первом уравнении данной системы запишем все степени как степени с основанием 3 (см. комментарий к задаче 2). После равносильных (на ОДЗ) преобразований первого уравнения получаем систему (1) (см. решение), в которую переменные входят только в виде 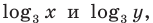 поэтому удобно произвести замену переменных. После обратной замены применяем определение логарифма.
поэтому удобно произвести замену переменных. После обратной замены применяем определение логарифма.
Решение:
ОДЗ: 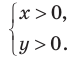 На этой ОДЗ первое уравнение данной системы равносильно уравнениям:
На этой ОДЗ первое уравнение данной системы равносильно уравнениям: 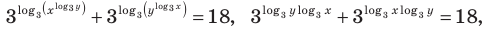
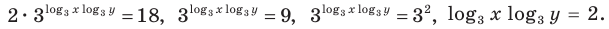
Тогда данная система уравнений равносильна системе
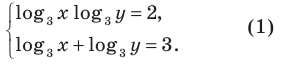
Замена 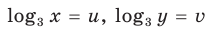 дает систему уравнений
дает систему уравнений 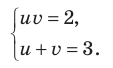 Из второго уравнения последней системы
Из второго уравнения последней системы 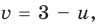 из первого уравнения получаем
из первого уравнения получаем 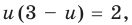 то есть
то есть 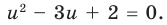 Отсюда
Отсюда 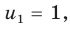
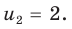 Тогда
Тогда 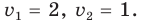 Обратная замена дает
Обратная замена дает
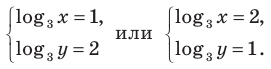
Тогда

(найденные решения входят в ОДЗ). Ответ: 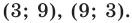
Пример №4
Решите неравенство 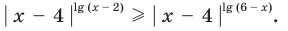
I способ
Комментарий:
Попытаемся выполнить равносильные преобразования данного неравенства, применив рассуждения, аналогичные тем, что приводились при решении показательно-степенных уравнений (см. пункт II табл. 60). Поскольку 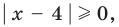 то из особых случаев следует рассмотреть только два: основание равно
то из особых случаев следует рассмотреть только два: основание равно 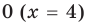 и основание равно
и основание равно 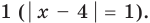 При других значениях
При других значениях 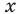 основание — положительное число, не равное 1.
основание — положительное число, не равное 1.
Рассмотрим два случая:
- 1) основание больше 1 (при переходе от степеней к показателям в данном неравенстве знак неравенства не меняется);
- 2) основание меньше 1, но больше 0 (при переходе от степеней к показателям знак неравенства меняется на противоположный). При таких преобразованиях получаем неравенства, равносильные данному (на его ОДЗ), поскольку можем гарантировать правильность не только прямых, но и обратных переходов.
При решении полученных простейших логарифмических неравенств учитываем, что функция 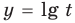 возрастающая. В ответ следует включить все решения полученных систем неравенств и все особые значения, которые являются решениями данного неравенства.
возрастающая. В ответ следует включить все решения полученных систем неравенств и все особые значения, которые являются решениями данного неравенства.
Решение:
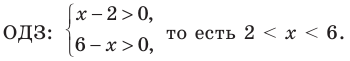
При 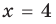 данное неравенство выполняется
данное неравенство выполняется 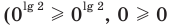 — верное неравенство), таким образом,
— верное неравенство), таким образом, 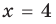 — одно из его решений. Если
— одно из его решений. Если 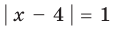 (то есть
(то есть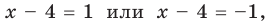 тогда
тогда 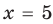 или
или 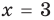 — эти значения входят в ОДЗ), то данное неравенство также выполняется. При
— эти значения входят в ОДЗ), то данное неравенство также выполняется. При 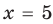 и
и 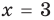 получаем верное неравенство
получаем верное неравенство  Таким образом , эти числа также являются решениями данного неравенства. При
Таким образом , эти числа также являются решениями данного неравенства. При 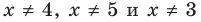 на ОДЗ данное неравенство равносильно следующей совокупности систем:
на ОДЗ данное неравенство равносильно следующей совокупности систем:
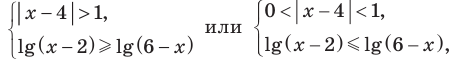
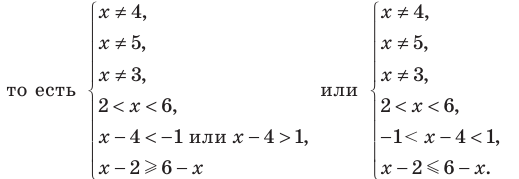
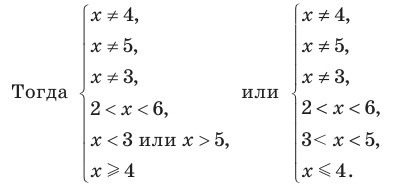
Таким образом, 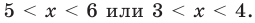 Учитывая особые значения , которые являются решениями, получаем:
Учитывая особые значения , которые являются решениями, получаем: 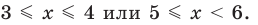 Ответ:
Ответ: 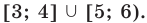
II способ
Комментарий:
Решим данное неравенство методом интервалов, для этого приведем его к виду 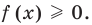 Для нахождения нулей
Для нахождения нулей 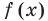 необходимо решить показательно-степенное уравнение (2) (см . решение ниже). Поскольку
необходимо решить показательно-степенное уравнение (2) (см . решение ниже). Поскольку 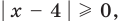 то из особых случаев необходимо рассмотреть только два — основание равно 0
то из особых случаев необходимо рассмотреть только два — основание равно 0 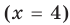 или основание равно
или основание равно 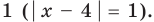 При других значениях
При других значениях 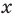 из ОДЗ в уравнении (3) (см. решение ниже) основание — положительное число, не равное 1. Тогда можно приравнять показатели степеней (получаем уравнение, равносильное данному). Для нахождения знаков
из ОДЗ в уравнении (3) (см. решение ниже) основание — положительное число, не равное 1. Тогда можно приравнять показатели степеней (получаем уравнение, равносильное данному). Для нахождения знаков 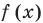 удобно использовать график функции
удобно использовать график функции 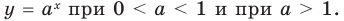
Решение:
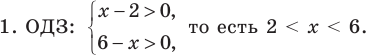
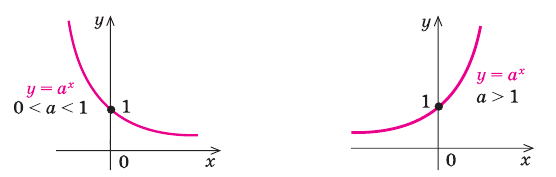
На этой ОДЗ данное неравенство равносильно неравенству
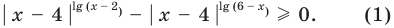
2. Пусть 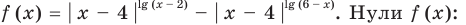
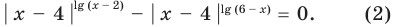
На ОДЗ уравнение (2) равносильно уравнению
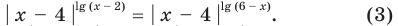
При 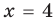 равенство (3) выполняется
равенство (3) выполняется 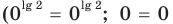 — верное равенство), таким образом,
— верное равенство), таким образом, 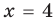 — корень уравнения (3). Если
— корень уравнения (3). Если 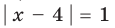 (то есть
(то есть 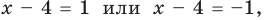 тогда
тогда 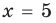 или
или 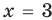 ), то равенство (3) также выполняется. При
), то равенство (3) также выполняется. При 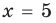 и
и 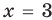 получаем верное равенство
получаем верное равенство 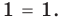 Таким образом, эти числа также являются корнями уравнения (3). При
Таким образом, эти числа также являются корнями уравнения (3). При 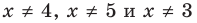 на ОДЗ уравнение (3) равносильно уравнению
на ОДЗ уравнение (3) равносильно уравнению 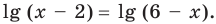 Тогда
Тогда 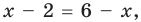 то есть
то есть 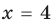 — не удовлетворяет условию
— не удовлетворяет условию 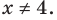 Следовательно, на последнем множестве уравнение (3) корней не имеет.
Следовательно, на последнем множестве уравнение (3) корней не имеет.
3. Отмечаем нули функции на ОДЗ и находим знак 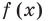 на каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).
на каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).

Ответ: 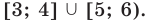
Пример №5
Решите неравенство 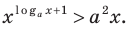
Комментарий:
На ОДЗ обе части неравенства положительны, поэтому попытаемся прологарифмировать обе его части. Поскольку в данное неравенство уже входит 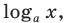 то удобно прологарифмировать по основанию
то удобно прологарифмировать по основанию 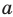 . Но при логарифмировании по основанию больше 1 знак неравенства не меняется, а при логарифмировании по основанию меньше 1 — меняется. Необходимо рассмотреть два случая (в каждом из них получаем неравенство, равносильное данному на его ОДЗ).
. Но при логарифмировании по основанию больше 1 знак неравенства не меняется, а при логарифмировании по основанию меньше 1 — меняется. Необходимо рассмотреть два случая (в каждом из них получаем неравенство, равносильное данному на его ОДЗ).
Решение:
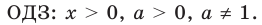
Прологарифмируем обе части неравенства.
1) При 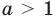 данное неравенство на его ОДЗ равносильно неравенствам:
данное неравенство на его ОДЗ равносильно неравенствам:
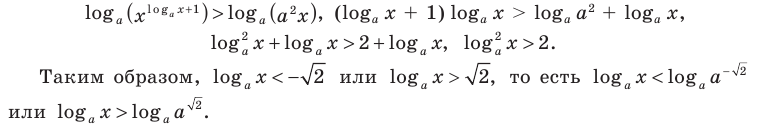
Учитывая ОДЗ  и то, что
и то, что получаем
получаем 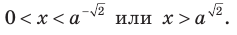 2) При
2) При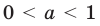 данное неравенство на его ОДЗ равносильно неравенствам:
данное неравенство на его ОДЗ равносильно неравенствам:
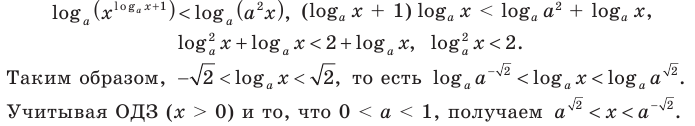
Ответ: 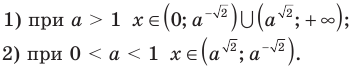
Показательно-степенные уравнения
Показательно-степенные уравнения:
Показательно-степенными уравнениями обычно называют уравнения, содержащие выражения вида 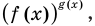 то есть уравнения вида
то есть уравнения вида 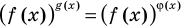 (основанием степеней, стоящих в левой и правой частях показательно степенного уравнения, является
(основанием степеней, стоящих в левой и правой частях показательно степенного уравнения, является 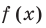 — выражение с переменной).
— выражение с переменной).
Основные способы решения уравнения вида 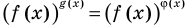
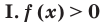
Используем (если возможно) основное логарифмическое тождество в виде 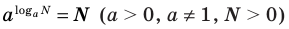
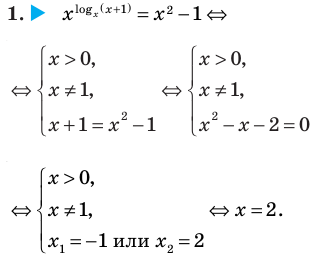
Ответ: 2
Логарифмируем (если возможно) обе части уравнения по числовому основанию или представляем все степени как степени с одним и тем же числовым основанием по формуле
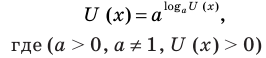
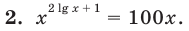
На ОДЗ 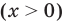 обе части уравнения положительны, поэтому после логарифмирования по основанию 10 получаем уравнение, равносильное данному:
обе части уравнения положительны, поэтому после логарифмирования по основанию 10 получаем уравнение, равносильное данному: 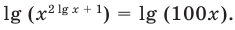
Отсюда 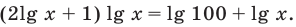
Замена: 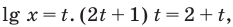
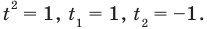 Тогда
Тогда 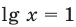 или
или 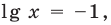 то есть
то есть 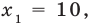
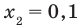 (оба корня входят в ОДЗ). Ответ: 10; 0,1.
(оба корня входят в ОДЗ). Ответ: 10; 0,1.
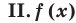 — произвольное выражение
— произвольное выражение
Две степени с одинаковыми основаниями 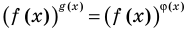 могут быть равными в одном из четырех случаев:
могут быть равными в одном из четырех случаев:
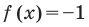 и для корней этого уравнения
и для корней этого уравнения 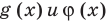 — целые числа одинаковой четности.
— целые числа одинаковой четности.-
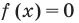 и для корней этого уравнения
и для корней этого уравнения 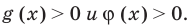
-
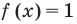 и для корней этого уравнения
и для корней этого уравнения 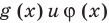 существуют.
существуют. -
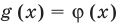 и для корней этого уравнения существуют
и для корней этого уравнения существуют 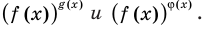
Пример:
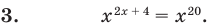
Если предположить, что основание степени 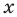 является числом, то сначала рассмотрим три особых случая (основание степени равно –
является числом, то сначала рассмотрим три особых случая (основание степени равно –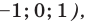 а затем приравняем показатели степеней:
а затем приравняем показатели степеней:
- при
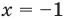 получаем верное равенство
получаем верное равенство 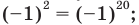
- при
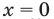
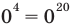 — верное равенство;
— верное равенство; - при
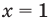
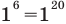 — верное равенство;
— верное равенство; - при
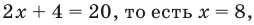 — верное равенство.
— верное равенство.
Ответ: 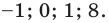
Замечание. Если предположить, что основание 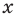 является переменной, то функция
является переменной, то функция 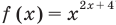 считается определенной только при
считается определенной только при 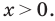 В этом случае данное уравнение имеет только корни 1 и 8, и получаем ответ: 1; 8. Таким образом, ответ к такому уравнению нельзя записать однозначно.
В этом случае данное уравнение имеет только корни 1 и 8, и получаем ответ: 1; 8. Таким образом, ответ к такому уравнению нельзя записать однозначно.
Объяснение и обоснование:
Показательно-степенными уравнениями и неравенствами обычно называют уравнения и неравенства, содержащие выражения вида 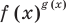 (в которых переменная входит и в основание, и в показатель степени).
(в которых переменная входит и в основание, и в показатель степени).
Анализируя показательно-степенные уравнения, представленные в таблице 57, следует помнить, что в школьном курсе математики понятие уравнения на разных этапах вводилось по-разному. А именно: в 4-5 классах уравнением называлось числовое равенство, содержащее неизвестное число, обозначенное буквой. Значение неизвестного, при котором уравнение обращается в верное числовое равенство, называлось корнем или решением этого уравнения. Например, для уравнения 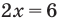 корнем является значение
корнем является значение 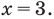
С точки зрения приведенного определения в уравнении 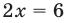 буквой
буквой 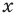 обозначено хотя и неизвестное нам, но конкретное число, поэтому
обозначено хотя и неизвестное нам, но конкретное число, поэтому 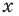 может принимать единственное значение
может принимать единственное значение 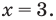 Но такое определение затрудняет в дальнейшем работу с уравнением. Когда
Но такое определение затрудняет в дальнейшем работу с уравнением. Когда 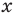 принимает единственное значение, мы не можем применять, например, графическое решение уравнения (имея только одно значение
принимает единственное значение, мы не можем применять, например, графическое решение уравнения (имея только одно значение 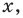 невозможно получить график
невозможно получить график 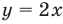 как прямую линию на плоскости). Поэтому, начиная с 6-7 классов, уравнение определяется как равенство с переменной (а корнем или решением уравнения соответственно называется такое значение переменной, при котором это уравнение обращается в верное числовое равенство). Тогда
как прямую линию на плоскости). Поэтому, начиная с 6-7 классов, уравнение определяется как равенство с переменной (а корнем или решением уравнения соответственно называется такое значение переменной, при котором это уравнение обращается в верное числовое равенство). Тогда 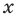 в уравнении
в уравнении 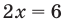 — это переменная, для которой нет ни одного ограничения, и поэтому
— это переменная, для которой нет ни одного ограничения, и поэтому 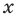 может быть любым числом (ОДЗ уравнения:
может быть любым числом (ОДЗ уравнения: 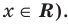 При таком подходе каждому значению переменной
При таком подходе каждому значению переменной 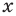 соответствует единственное значение переменной
соответствует единственное значение переменной 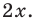 Таким образом, это уравнение можно решить графически, построить графики функций
Таким образом, это уравнение можно решить графически, построить графики функций 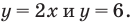 Кроме того, при таком подходе можно записать уравнение в общем виде как равенство
Кроме того, при таком подходе можно записать уравнение в общем виде как равенство 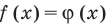 и обоснованно применить свойства функций для решения уравнений.
и обоснованно применить свойства функций для решения уравнений.
Для всех видов уравнений, которые рассматривались в курсе алгебры или алгебры и начал анализа, приведенные два определения уравнения приводят к одному тому же результату при решении уравнений. Но в случае показательно-степенного уравнения иногда можно получить разные ответы, используя разные подходы к определению уравнения.
Например, решим уравнение 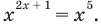
Если рассматривать такое уравнение как числовое равенство, то две степени с одинаковым основанием 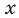 могут быть равными только в одном из четырех случаев. А именно: если основанием степени является одно из значений
могут быть равными только в одном из четырех случаев. А именно: если основанием степени является одно из значений 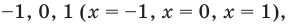 то степени могут быть равными даже тогда, когда их показатели будут разными (при условии, что эти степени существуют). Во всех остальных случаях степени с одинаковым основанием будут равными только тогда, когда показатели этих степеней будут равными
то степени могут быть равными даже тогда, когда их показатели будут разными (при условии, что эти степени существуют). Во всех остальных случаях степени с одинаковым основанием будут равными только тогда, когда показатели этих степеней будут равными 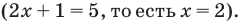 Следовательно, для получения всех корней данного уравнения достаточно проверить значения
Следовательно, для получения всех корней данного уравнения достаточно проверить значения 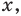 равные-1, 0,1, 2. Все эти числа являются корнями, так как при подстановке каждого из них в данное уравнение оно обращается в верное числовое равенство. Если же рассматривать это уравнение как равенство с переменной и встать на функциональную точку зрения, то функция
равные-1, 0,1, 2. Все эти числа являются корнями, так как при подстановке каждого из них в данное уравнение оно обращается в верное числовое равенство. Если же рассматривать это уравнение как равенство с переменной и встать на функциональную точку зрения, то функция 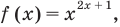 как правило, считается определенной только при
как правило, считается определенной только при 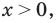 и тогда данное уравнение имеет только два корня:1 и 2.
и тогда данное уравнение имеет только два корня:1 и 2.
Таким образом, в рассмотренном уравнении ответ нельзя записать однозначно (поскольку каждый из указанных подходов к определению уравнения имеет право на существование и реально используется в математике). Поэтому в подобных ситуациях приходится приводить оба варианта ответа. Аналогичный пример приведен в таблице 57.
Обобщая приведенные выше рассуждения, заметим, что в том случае, когда при решении уравнения вида 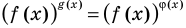 из условия не следует, что основание степени
из условия не следует, что основание степени 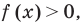 необходимо рассматреть три особых случая: основание
необходимо рассматреть три особых случая: основание 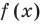 равно-1, 0, 1 (понятно, что в этих случаях степени
равно-1, 0, 1 (понятно, что в этих случаях степени 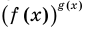 и
и 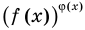 могут быть равными даже тогда, когда показатели
могут быть равными даже тогда, когда показатели 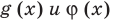 разные), а затем приравнять показатели
разные), а затем приравнять показатели 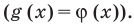 Если же из условия следует, что
Если же из условия следует, что 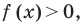 то рассматриваем только один особый случай — основание степени равно
то рассматриваем только один особый случай — основание степени равно 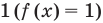 — и приравниваем показатели степеней
— и приравниваем показатели степеней 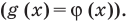
Например, решим уравнение 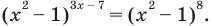
Из условия не следует, что основание степени 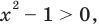 следовательно, приходится рассматривать все случаи. 2 2
следовательно, приходится рассматривать все случаи. 2 2
1) Если 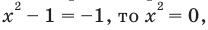 и тогда
и тогда 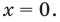
Подставляя это значение в данное уравнение, имеем 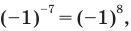 то есть
то есть 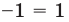 (неверное равенство). Таким образом,
(неверное равенство). Таким образом, 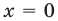 не является корнем данного уравнения.
не является корнем данного уравнения.
2) Если 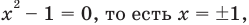 то при этих значениях
то при этих значениях 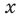 данное уравнение обращается в неверное числовое равенство (поскольку значения выражений
данное уравнение обращается в неверное числовое равенство (поскольку значения выражений 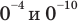 не существуют). Таким образом, числа 1 и -1 не являются корнями данного уравнения.
не существуют). Таким образом, числа 1 и -1 не являются корнями данного уравнения.
3) Если 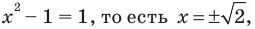 данное уравнение обращается в верное равенство
данное уравнение обращается в верное равенство 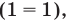 следовательно,
следовательно, 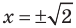 —корни данного уравнения.
—корни данного уравнения.
4) Приравняем показатели степеней данного уравнения (основания степеней в левой и правой частях уравнения одинаковые):  тогда
тогда 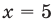 (при подстановке получаем верное равенство
(при подстановке получаем верное равенство 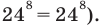
Объединяя полученные результаты, получаем ответ.
Ответ: 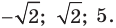
Замечание. При 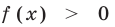 для решения уравнения вида
для решения уравнения вида 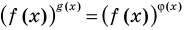 можно прологарифмировать обе его части по любому числовому основанию, получить равносильное уравнение, в котором уже не придется рассматривать особый случай — он будет учтен автоматически. Это связано с тем, что функция
можно прологарифмировать обе его части по любому числовому основанию, получить равносильное уравнение, в котором уже не придется рассматривать особый случай — он будет учтен автоматически. Это связано с тем, что функция 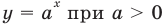 имеет особый случай, если
имеет особый случай, если 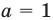 (см. график функции
(см. график функции 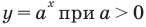 на с. 338), а функция
на с. 338), а функция 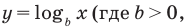
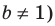 особых случаев не имеет.
особых случаев не имеет.
Также отметим, что при решении неравенств вида 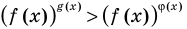 обычно используют функциональный подход и считают, что
обычно используют функциональный подход и считают, что 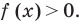
Заметим, что в тех случаях, когда в показательно-степенное уравнение входят выражения вида 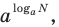 то для решения такого уравнения может использоваться основное логарифмическое тождество. В этом случае следует учитывать ОДЗ данного уравнения (см. пример 1 в табл. 57).
то для решения такого уравнения может использоваться основное логарифмическое тождество. В этом случае следует учитывать ОДЗ данного уравнения (см. пример 1 в табл. 57).
Достаточно часто для решения показательно-степенных уравнений используется логарифмирование обеих частей. Конечно, это можно сделать только тогда, когда на ОДЗ данного уравнения обе части уравнения положительны (см. пример 2 в табл. 57).
Приведем еще несколько примеров решения показательно-степенных уравнений и неравенств.
Пример №6
Решите уравнение 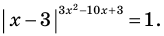
Решение:
Поскольку 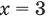 не является корнем данного уравнения
не является корнем данного уравнения 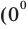 не существует), то при
не существует), то при 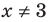 обе его части положительны . После логарифмирования (по основанию 10) обеих частей данного уравнения получаем равносильные ему уравнения:
обе его части положительны . После логарифмирования (по основанию 10) обеих частей данного уравнения получаем равносильные ему уравнения:
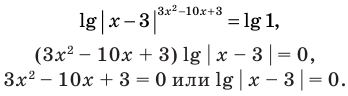
Из первого полученного уравнения имеем 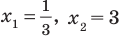 (не является корнем), а из второго
(не является корнем), а из второго 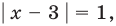 тогда
тогда 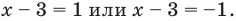 То есть
То есть 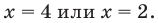
Ответ: 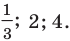
Комментарий:
Поскольку 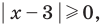 то из особых случаев можно рассмотреть только один — основание равно
то из особых случаев можно рассмотреть только один — основание равно 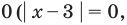 то есть
то есть 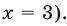 Чтобы не рассматривать случай, когда основание равно 1, достаточно при
Чтобы не рассматривать случай, когда основание равно 1, достаточно при 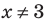 прологарифмировать обе части уравнения по числовому основанию (например, по основанию 10).
прологарифмировать обе части уравнения по числовому основанию (например, по основанию 10).
При 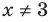 обе части данного уравнения положительны, поэтому после логарифмирования получаем уравнение, равносильное данному. Поскольку все дальнейшие преобразования являются равносильными (при
обе части данного уравнения положительны, поэтому после логарифмирования получаем уравнение, равносильное данному. Поскольку все дальнейшие преобразования являются равносильными (при 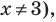 то все полученные решения (не равные 3) являются корнями данного уравнения.
то все полученные решения (не равные 3) являются корнями данного уравнения.
Пример №7
Решите уравнение 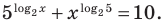
Комментарий:
Прологарифмировать обе части данного уравнения не удается (в левой части стоит сумма), поэтому попытаемся все степени представить в виде степеней с одним и тем же числовым основанием. Учитывая, что в данном уравнении есть логарифм по основанию 2, представим все данные степени как степени с основанием 2 по формуле 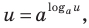 где
где 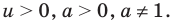 Тогда
Тогда
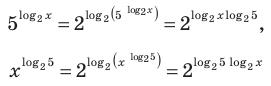
(то есть слагаемые, стоящие в левой части данного уравнения, одинаковы). После получения уравнения (2) (см. решение) можно использовать равенство (1) справа налево. Можно также записать правую часть уравнения (2) как степень числа 2 или прологарифмировать обе его части по основанию 2.
Решение:
► ОДЗ: х > 0. На этой ОДЗ данное уравнение равносильно уравнениям:
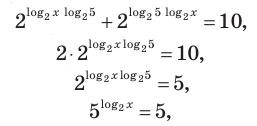
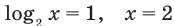 (принадлежит ОДЗ).
(принадлежит ОДЗ).
Ответ: 2.
Комментарий:
Используем равносильные преобразования системы. Для этого учтем ОДЗ и проследим за тем, чтобы на этой ОДЗ все преобразования уравнений как в прямом, так и в обратном направлении сохраняли верные равенства.
В первом уравнении данной системы запишем все степени как степени с основанием 3 (см. выше комментарий к задаче 2). После равносильных (на ОДЗ) преобразований первого уравнения получаем систему (1) (см. решение), в которую переменные входят только в виде 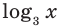 и
и 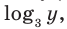 поэтому удобно использовать замену переменных. После обратной замены применяем определение логарифма.
поэтому удобно использовать замену переменных. После обратной замены применяем определение логарифма.
Решение:
ОДЗ: 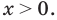 На этой ОДЗ первое уравнение заданной системы равносильно уравнениям:
На этой ОДЗ первое уравнение заданной системы равносильно уравнениям:
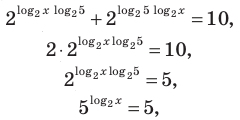
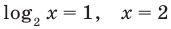 принадлежит ОДЗ.
принадлежит ОДЗ.
Пример №8
Решите систему уравнений 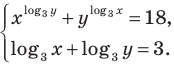
Комментарий:
Используем равносильные преобразования системы. Для этого учтем ОДЗ и проследим за тем, чтобы на этой ОДЗ все преобразования уравнений как в прямом, так и в обратном направлении сохраняли верные равенства.
В первом уравнении данной системы запишем все степени как степени с основанием 3 (см. выше комментарий к задаче 2). После равносильных (на ОДЗ) преобразований первого уравнения получаем систему (1) (см. решение), в которую переменные входят только в виде 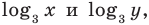 поэтому удобно использовать замену переменных. После обратной замены применяем определение логарифма.
поэтому удобно использовать замену переменных. После обратной замены применяем определение логарифма.
Решение:
ОДЗ: 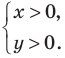 На этой ОДЗ первое уравнение заданной системы равносильно уравнениям:
На этой ОДЗ первое уравнение заданной системы равносильно уравнениям: 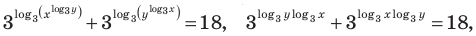
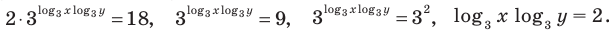
Тогда заданная система равносильна системе
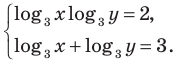
Замена 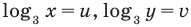 дает систему
дает систему 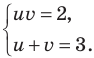
Из второго уравнения последней системы 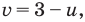 тогда из первого уравнения
тогда из первого уравнения 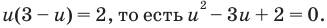 Отсюда
Отсюда 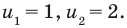 Тогда
Тогда 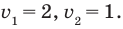
Обратная замена дает
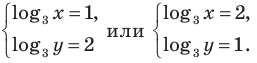
Тогда 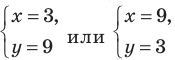 (найденные решения входят ОДЗ)
(найденные решения входят ОДЗ)
Ответ: 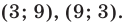
Пример №9
Решите неравенство 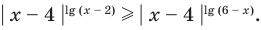
I способ
Комментарий:
Попытаемся выполнить равносильные преобразования данного неравенства, применив рассуждения, аналогичные тем, что приводились при решении показательно-степенных уравнений (см. пункт II табл. 57). Поскольку 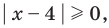 то из особых случаев необходимо рассмотреть только два: основание равно 0 (то есть
то из особых случаев необходимо рассмотреть только два: основание равно 0 (то есть 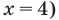 и основание равно 1 (то есть
и основание равно 1 (то есть 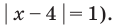 При других значениях
При других значениях 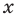 основание — положительное число, не равное 1. Рассмотрим два случая: 1) основание больше 1 (при переходе от степеней к показателям в данном неравенстве знак неравенства не меняется); 2) основание меньше 1, но больше 0 (при переходе от степеней к показателям в данном неравенстве знак неравенства меняется на противоположный). При таких преобразованиях получаем неравенства, равносильные данному (на его ОДЗ), поскольку можем гарантировать правильность не только прямых, но и обратных переходов.
основание — положительное число, не равное 1. Рассмотрим два случая: 1) основание больше 1 (при переходе от степеней к показателям в данном неравенстве знак неравенства не меняется); 2) основание меньше 1, но больше 0 (при переходе от степеней к показателям в данном неравенстве знак неравенства меняется на противоположный). При таких преобразованиях получаем неравенства, равносильные данному (на его ОДЗ), поскольку можем гарантировать правильность не только прямых, но и обратных переходов.
При решении полученных простейших логарифмических неравенств учитываем, что функция 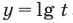 является возрастающей.
является возрастающей.
В ответ следует включить все решения полученных систем неравенств и все особые значения, которые являются решениями данного неравенства.
Решение:
ОДЗ: 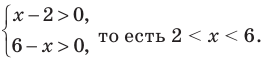 При
При 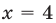 данное неравенство выполняется
данное неравенство выполняется 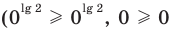 — верное неравенство), таким образом,
— верное неравенство), таким образом, 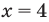 — одно из решений этого неравенства.
— одно из решений этого неравенства.
Если 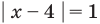 (то есть
(то есть 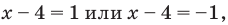 тогда
тогда 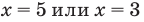 — эти значения входят в ОДЗ), то данное неравенство также выполняется. При
— эти значения входят в ОДЗ), то данное неравенство также выполняется. При 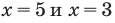 получаем верное неравенство
получаем верное неравенство 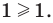 Таким образом, эти числа также являются решениями данного неравенства.
Таким образом, эти числа также являются решениями данного неравенства.
При 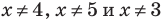 на ОДЗ данное неравенство равносильно следующей совокупности систем:
на ОДЗ данное неравенство равносильно следующей совокупности систем: 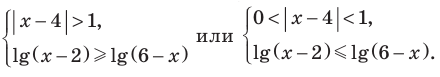 То есть
То есть 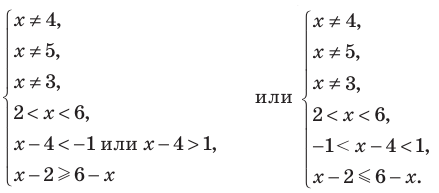
Тогда: 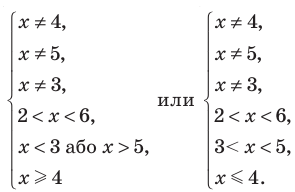
Таким образом, 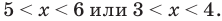 Учитывая особые значения, которые являются решениями, получаем:
Учитывая особые значения, которые являются решениями, получаем: 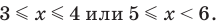
Ответ: 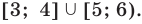
II способ решения неравенства 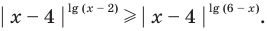
Комментарий:
Решим данное неравенство методом интервалов, для этого приведем его к виду 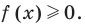
Для нахождения нулей 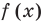 необходимо решить показательно-степенное уравнение (2). Поскольку
необходимо решить показательно-степенное уравнение (2). Поскольку 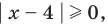 то из особых случаев необходимо рассмотреть только два — основание равно 0 (то есть
то из особых случаев необходимо рассмотреть только два — основание равно 0 (то есть 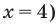 или основание равно 1 (то есть
или основание равно 1 (то есть 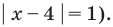 При других значениях
При других значениях 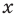 из ОДЗ в уравнении (3) основание — положительное число, не равное 1. Тогда можно приравнять показатели степеней (получаем уравнение, равносильное данному).
из ОДЗ в уравнении (3) основание — положительное число, не равное 1. Тогда можно приравнять показатели степеней (получаем уравнение, равносильное данному).
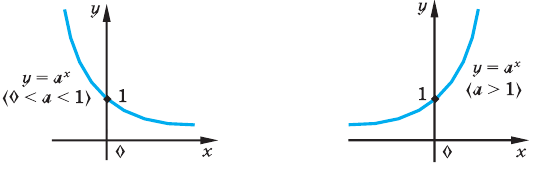
Для нахождения знаков 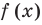 удобно использовать графики функции
удобно использовать графики функции 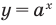 при
при 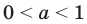 и при
и при 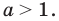
Решение:
1. ОДЗ 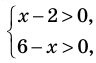 то есть
то есть 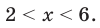
На этой ОДЗ данное неравенство равносильно неравенству
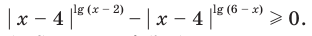
2. Пусть 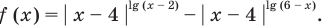 Нули
Нули 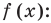
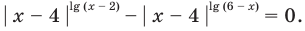
На ОДЗ уравнение (2) равносильно уравнению
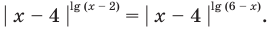
При 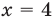 равенство (3) выполняется
равенство (3) выполняется 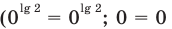 — верное равенство), таким образом,
— верное равенство), таким образом, 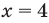 — корень уравнения (3).
— корень уравнения (3).
Если 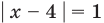 (то есть
(то есть 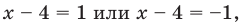 тогда
тогда 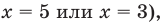 то равенство (3) также выполняется. При
то равенство (3) также выполняется. При 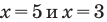 получаем верное равенство
получаем верное равенство 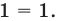 Таким образом, эти числа также являются корнями уравнения (3). При
Таким образом, эти числа также являются корнями уравнения (3). При 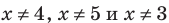 на ОДЗ уравнение (3) равносильно уравнению
на ОДЗ уравнение (3) равносильно уравнению 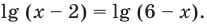 Тогда
Тогда 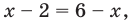 то есть
то есть 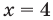 — не удовлетворяет условию
— не удовлетворяет условию 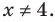 Следовательно, на последнем множестве уравнение (3) корней не имеет.
Следовательно, на последнем множестве уравнение (3) корней не имеет.
3. Отмечаем нули функции на ОДЗ и находим знак 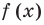 на каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).
на каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).
Ответ: 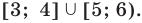

Пример №10
Решите неравенство 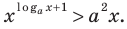
Комментарий:
На ОДЗ обе части неравенства положительны, поэтому попытаемся прологарифмировать обе части неравенства. Поскольку в данное неравенство уже входит 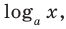 то удобно прологарифмировать по основанию
то удобно прологарифмировать по основанию 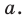 Но при логарифмировании по основанию больше 1 знак неравенства не меняется, а при логарифмировании по основанию меньше 1 знак неравенства меняется. Приходится рассматривать два случая (в каждом из них получаем неравенство, равносильное данному на его ОДЗ).
Но при логарифмировании по основанию больше 1 знак неравенства не меняется, а при логарифмировании по основанию меньше 1 знак неравенства меняется. Приходится рассматривать два случая (в каждом из них получаем неравенство, равносильное данному на его ОДЗ).
Решение:
ОДЗ: 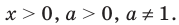
Прологарифмируем обе части неравенства.
1) При 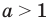 данное неравенство на его ОДЗ равносильно неравенствам:
данное неравенство на его ОДЗ равносильно неравенствам:
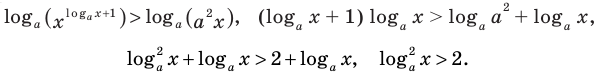
Таким образом, 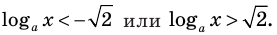
To есть 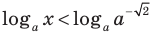 или
или 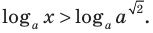
Учитывая ОДЗ 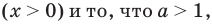 получаем
получаем 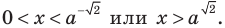
2) При 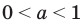 данное неравенство на его ОДЗ равносильно неравенствам:
данное неравенство на его ОДЗ равносильно неравенствам:
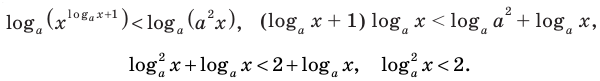
Таким образом,
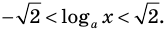
То есть 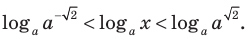
Учитывая ОДЗ 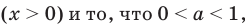 получаем
получаем 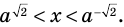
Ответ: 1)при 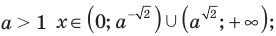 2) при
2) при 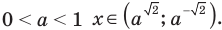
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Показательные уравнения и неравенства
- Логарифмические уравнения и неравенства
- Степенная функция - определение и вычисление
- Степень с целым показателем
- Логарифмическая функция, её свойства и график
- Логарифмические выражения
- Показательная функция, её график и свойства
- Производные показательной и логарифмической функций