Плоскость в трехмерном пространстве с примерами решения

Содержание:

Общее уравнение плоскости:

Пусть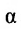

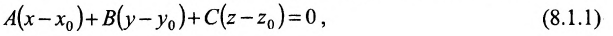
которое называется уравнением плоскости, проходящей через точку 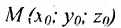и имеющей нормальный вектор 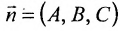. Его можно преобразовать к виду

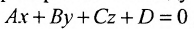(8.1.2)

где 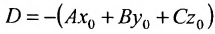. Уравнение (8.1.2) называется общим уравнением плоскости.

Приведём уравнение плоскости (8.1.2) к специальному виду. Для этого перенесём свободный член в правую часть уравнения: .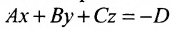

Разделим обе части уравнения на —D получим:

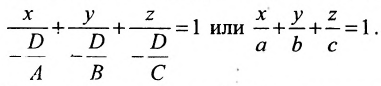(8.1.3)

Это и есть специальный вид уравнения плоскости или уравнение плоскости "в отрезках", где а, b, с - величины отрезков, которые отсекает плоскость на координатных осях.

Если плоскость проходит через точки 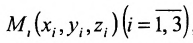, не лежащие на одной прямой, то её уравнение можно записать в виде

Разложив данный определитель по элементам первой строки, придём к уравнению вида (8.1.1).

Уравнения (8.1.1), (8.1.3), (8.1.4) можно привести к виду (8.1.2).

Пример:

Составить уравнение плоскости, проходящей через точки А(0, -2, -1), В(2, 4, -2) и С(3, 2, 0).

Решение:

Воспользуемся формулой (8.1.4), где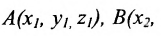

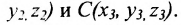
Подставив координаты точек A, В и С, получим: 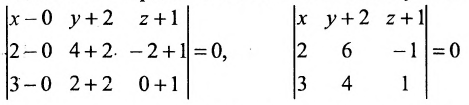Разложим определитель по элементам первой строки: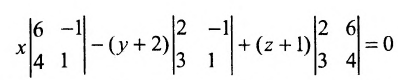Вычислив три определителя второго порядка, получим уравнение: 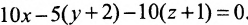. Сократив на 5 и приведя подобные, найдем уравнение искомой плоскости АВС: .

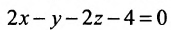Взаимное расположение двух плоскостей, прямой и плоскости

Углом между прямой и плоскостью будем называть угол, образованный прямой и ее проекцией на плоскость (рис. 8.1). Пусть прямая L и плоскость а заданы уравнениями:

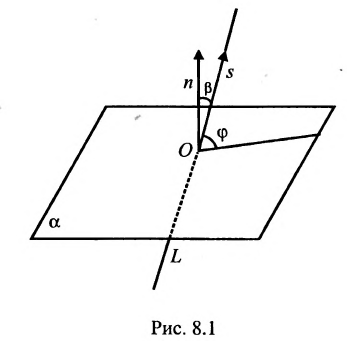
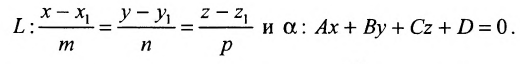
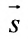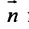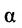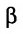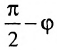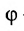Рассмотрим направляющий вектор прямой L и нормальный вектор плоскости (рис. 8.1). Если угол между ними острый, то его можно представить в виде разности, где - угол между прямой L й плоскостью 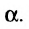. Тогда косинус угла между векторам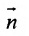и и 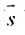равен синусу угла между прямой L и плоскостью 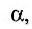т.е.

.

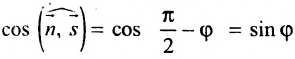Если угол 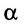между векторами 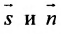тупой, то его можно представить в виде суммы 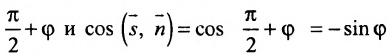. Поэтому в любом случае 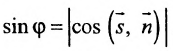. Воспользовавшись формулой вычисления косинуса угла между векторами, получим формулу и для вычисления угла между прямой L и плоскостью:

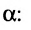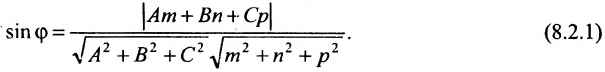
Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор 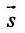прямой L и нормальный вектор 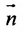плоскости 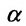коллинсарны, т.е. их координаты пропорциональны:

Условие параллельности прямой и плоскости. Прямая L и плоскость 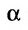параллельны тогда и только тогда, когда векторы 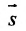и

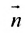перпендикулярны, т.е. их скалярное произведение равно нулю: 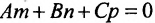(8.2.3)

Пример:

Написать уравнение плоскости, проходящей через точку 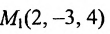параллельно прямым 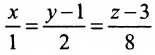и

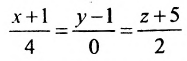
Решение:

Так как 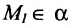, то уравнение плоскости будем искать в виде

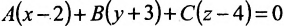
Применяя условие параллельности (8.2.3) прямой и плоскости, получим систему линейных уравнений

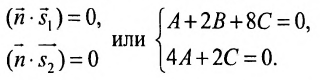
где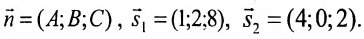

Решив систему, найдем:

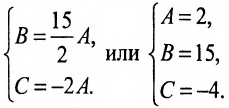
Подставив найденные значения коэффициентов А,В,С, полУ~ чим искомое уравнение плоскости:

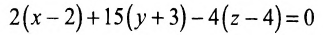
или

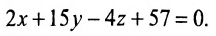
Угол между плоскостями. Рассмотрим две плоскости 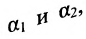заданные соответственно уравнениями:

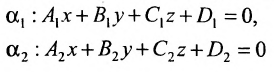
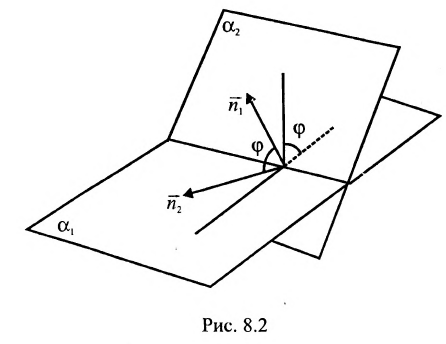
Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно,

что угол между нормальными векторами 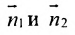плоскостей 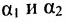равен одному из указанных смежных двугранных углов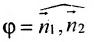

или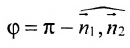 .Поэтому 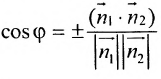. Т.к. 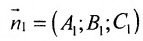и

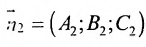, то

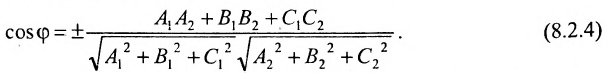
Пример:

Определить угол между плоскостями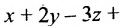

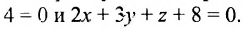
Решение:

Воспользовавшись формулой (8.2.4), получим:

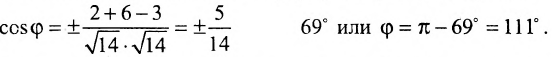
Условие параллельности двух плоскостей. Две плоскости 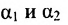параллельны тогда и только тогда, когда их нормальные векторы 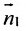и 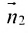параллельны.

Векторы параллельны, если их координаты пропорциональны:

Две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы 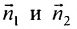перпендикулярны. Следовательно, их скалярное произведение равно нулю: 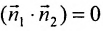, или 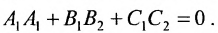(8.2.6)

Пример:

Составить уравнение плоскости, проходящей через точку M(-2, 1, 4) параллельно плоскости .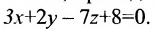

Решение:

Уравнение плоскости будем искать в виде 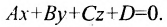. Из условия параллельности плоскостей следует, что: 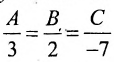. Положив А=3, В=2, С=-7, получим уравнение плоскости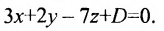

Так как 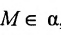, то координаты этой точки удовлетворяют уравнению. Подставив координаты точки, - 6+2 - 28+D=0, найдем D = 32. Тогда искомое уравнение плоскости будет иметь вид: 3х + 2у -7z + 32=0.

Пример:

Составить уравнение плоскости, проходящей через точки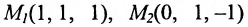перпендикулярно плоскости x+y+z=0.

Решение:

Так как 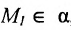, то используя уравнение плоскости, проходящей через заданную точку, будем иметь

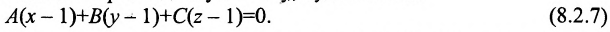
Далее, так как 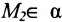, то подставив координаты точки в записанное уравнение, получим равенство -А-2С = 0 или А + 2С = 0.

Учитывая, что заданная плоскость перпендикулярна искомой, составим еще одно уравнение: A+B+С=0. Получим систему:

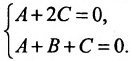
Выразив коэффициенты А и В через С: А = -2 С, В=С и подставив их в уравнение (8.2.7), -2С (х-1)+С (у-1)+С (z-l)=0, определяем искомое уравнение: —2х + у +z = 0 .

Понятие гиперплоскости

Взаимное расположение гиперплоскостей:

Рассмотрим n-мерное векторное пространство Пусть вектор 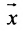этого пространства имеет координаты 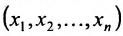. По аналогии с пространством 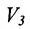, естественно считать, что и в n-мерном векторном пространстве 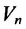координаты 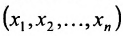произвольного вектора 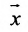являются в то же время координатами некоторой точки М пространства 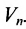. Тогда вектор х назовём радиус-вектором точки М Следовательно, каждому вектору можно поставить в соответствие точку и мы получим n-мерное точечное пространство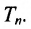. Точка О с координатами (О, 0, ...,0) называется началом координат. Ей отвечает нулевой вектор. Геометрическое место точек 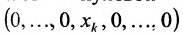называется координатной осью. Следовательно. в имеется n координатных осей: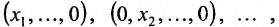

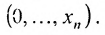
Совокупность точек 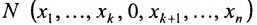называется координатной гиперплоскостью .

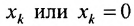Определение 8.3.1. Гиперплоскостью в п-мериом пространстве 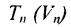называется геометрическое место точек, координаты которых удовлетворяют линейному (векторному) уравнению:

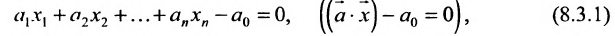
где 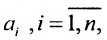- произвольные действительные числа.

Заметим, что все 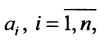не могут равняться нулю.

Рассмотрим две гиперплоскости:

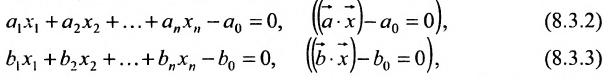
Множество точек, принадлежащих как первой, так и второй гиперплоскости, называется их пересечением.

Теорема 8.3.1. Две гиперплоскости (8.3.2) и (8.3.3) не пересекаются в том и только в том случае, когда коэффициенты при соответствующих неизвестных пропорциональны, а свободные члены находятся в ином отношении:

Доказательство. Пусть гиперплоскости (8.3.2) и (8.3.3) не пересекаются. Следовательно, они не имеют общих точек и система

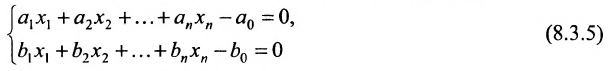несовместна.

И наоборот, если система несовместна, то гиперплоскости (8.3.2) и (8.3.3) не пересекаются.

В силу теоремы Кронекера- Капелли система (8.3.5) несовместна, если ранг матрицы не равен рангу расширенной матрицы системы. А так как ранг расширенной матрицы системы не больше 2, то ранг матрицы системы должен ть равен 1. Эта возможность выражается условием (8.3.4).Поскольку для того, чтобы матрица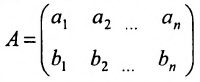 имела ранг r = 1, нужно, чтобы строки были линейно зависимы, т.е. пропорциональны.

Ранг матрицы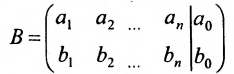 будет равен двум, если существует хотя бы один определитель второго порядка не равный нулю, т.е. если строки не пропорциональны. Теорема доказана.

Теорема 8.3.2. Для того, чтобы уравнения (8.3.2) и (8.3.3) определят одну и ту же гиперплоскость, необходимо и достаточно, чтобы выполнялись условия:

Доказательство. Достаточность. Пусть условия (8.3.6) выполнены. Обозначим отношения через t, т.е.

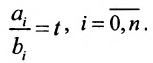
Тогда уравнение (8.3.2) можно получить из (8.3.3) умножением всех его членов на t. Поэтому уравнения равносильны и, следовательно, определяют одну и ту же гиперплоскость.

Необходимость. Пусть уравнения (8.3.2) и (8.3.3) определяют одну и ту же гиперплоскость. Система (8.3.5) совместна и, следовательно, ранг матрицы системы равен рангу расширенной матрицы. И т.к. эта система определяет одну гиперплоскость, то каждое из уравнений можно рассматривать как систему. Поэтому ранг этой системы равен 1 и все миноры второго порядка равны нулю, т.е.

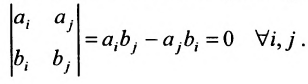
Откуда следует, что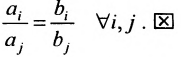

Определение 8.3.2. Две гиперплоскости называются параллель-ными, если они не пересекаются или совпадают.

Тогда из теорем 8.3.1 и 8.3.2 вытекает

Теорема 8.3.3. Две гиперплоскости (8.3.2) и (8.3.3) параллельны тогда и только тогда, когда соответствующие коэффициенты

пропорциональны, т.е.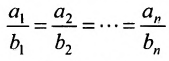

Введем понятие прямой в n мерном пространстве по аналогии с параметрическими уравнениями прямой в трехмерном пространстве.

Определение 8.3.3. Прямой в 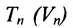называется множество точек 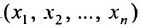(или векторов 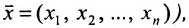, удовлетворяющих уравнениям:

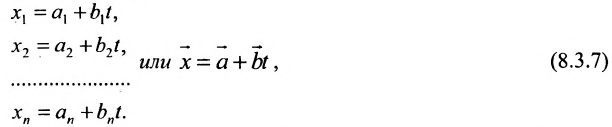
где 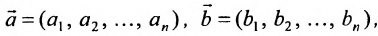, a t- переменный параметр, .

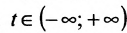Определение 8.3.4. Отрезком в 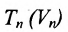называется множество точек 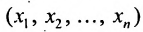(или векторов 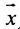), удовлетворяющих уравнениям (8.3.7) при изменении параметра t в закрытом интервале 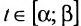. Точки 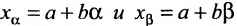называются концами отрезка.

Теорема 8.3.4. Всякая точка отрезка может быть выражена линейной комбинацией его концов:

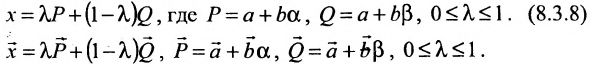
Если в трехмерном пространстве провести плоскость, то она разделит его на две части, называемые полупространствами. Очевидно, и гиперплоскость разделит n-мерное пространство на полупространства, т.е. справедливо.

Определение 8.3.5. Полупространствами, порождаемыми гиперплоскостью 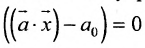называются два множества точек, удовлетворяющих соответственно условиям:

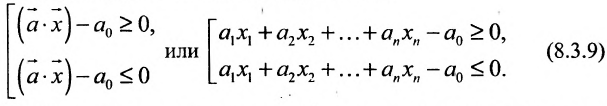
Гиперплоскость принадлежит обоим полупространствам, является их общей частью. Из (8.3.9) следует, что любое линейное неравенство геометрически определяет полупространство соответствующей размерности.

Определение 8.3.6. Множество точек 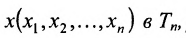удовлетворяющих условию 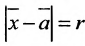или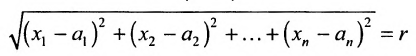 называется гиперсферой с центром в точке 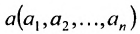и радиусом r.

• Заказать решение задач по высшей математике

Системы m линейных неравенств с n неизвестными

В элементарной математике мы познакомились с линейными неравенствами одного или двух переменных:

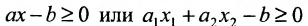
Решением таких неравенств является промежуток числовой оси или полуплоскость.

Рассмотрим теперь линейное неравенство с n переменными:

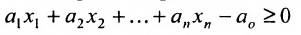в n-мерном пространстве.

Несколько неравенств, рассматриваемых совместно, образуют систему:

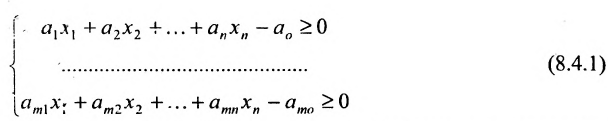
Определение 8.4.1. Областью решений системы т неравенств с п неизвестными называется множество точек пространства 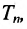координаты которых удовлетворяют каждому из неравенств системы.

Из того факта, что областью решения линейного неравенства является полупространство, вытекает

Теорема 8.4.1. Область решений системы линейных неравенств есть пересечение некоторого числа полупространств.

Это пересечение является выпуклым множеством; оно ограничено гиперплоскостями

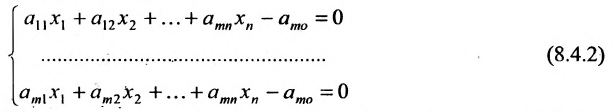
Так как линейные неравенства (8.4.1) независимы, то система (8.4.2) при m-n будет либо определённой, либо несовместной. И, следовательно, пересечение n гиперплоскостей в n-мерном пространстве либо даёт точку, либо не содержит ни одной точки.

Так как число систем по n уравнений с n неизвестными, которое может быть получено из (8.4.2) не может быть сколь угодно большим, и так как не всякая точка пересечения гиперплоскостей (является решением) принадлежит пересечению всех m гиперплоскостей, то число крайних точек, т.е. точек пересечения гиперплоскостей, принадлежащих данному множеству, ограничено. Следовательно, рассматриваемое множество будет многогранником, а крайние точки - его вершинами.

Итак, .областью решений совместной системы линейных нера-qchqtb является выпуклый многогранник, гранями которого служат некоторые части гиперплоскостей.

Пример:

Найти решение системы линейных неравенств

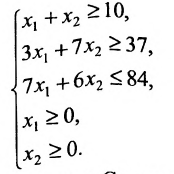
Решение:

Строим на плоскости граничные прямые:

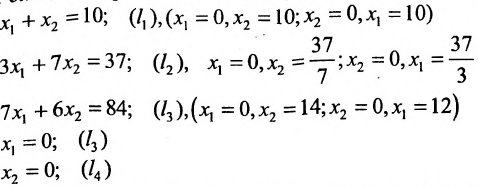
соответствующие заданным неравенствам (рис. 8.3). Каждая из них делит плоскость на две полуплоскости, одна из которых является решением соответствующего неравенства. Для выбора полуплоскости, являющейся решением неравенства, подставляем начало координат О (0, 0) в каждое неравенство. Если получаем верное неравенство, то полуплоскость, содержащая начало координат, является решением неравенства, в противном случае - полуплоскость, не содержащая начало координат, является решением неравенства.

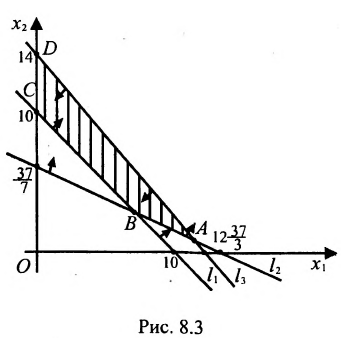
Стрелки указывают полуплоскости, являющиеся областями решений данных неравенств. Пересечение отмеченных полуплоскостей- заштрихованный четырехугольник АВСД на рис. 8.3- область решения данной системы.

Применение систем линейных неравенств в экономических исследованиях

Рассмотрим систему m линейных неравенств с n переменными:

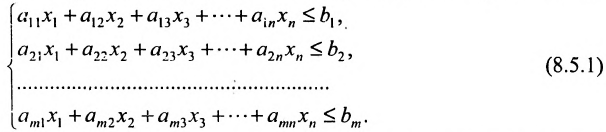
Каждое неравенство системы определяет полупространство. Решением системы (8.5.1) является пересечение этих полупространств.

Системы линейных неравенств широко применяются во многих экономических задачах, в частности, при построении линейной модели производства. Производственный способ описывает производство продукции и расход ресурсов в единицу времени. Он математически задается вектором выпуска или вектором валовой продукции и вектором 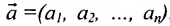называемым вектором затрат, отвечающим выпуску x.

Если в производственной системе используется m видов производственных ресурсов, определены запасы ресурса i при использовании j-той технологии, то модель производственной системы математически приобретает вид системы линейных неравенств (8.5.1), в которой .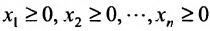

Пример:

Пусть известно содержание питательных веществ в единице каждого из имеющихся в хозяйстве кормов. Известна также цена каждого корма. Требуется определить все возможные рационы для кормления скота, которые удовлетворяли бы суточную потребность в каждом питательном веществе, а общая стоимость используемых кормов не превосходила бы A.

Решение:

Введем обозначения: m — число питательных веществ; n — число изменяющихся видов кормов; 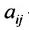—количество единиц i -го питательного вещества в единице j -го корма; 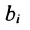— дневная потребность в / -ом питательном веществе; 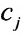—стоимость единицы j -го корма; 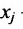—количество единиц j-го корма, используемого в рационе .

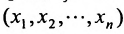Задача рациона формулируется следующим образом: определить рацион 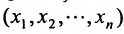, удовлетворяющий условиям:

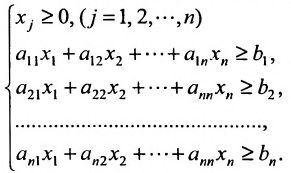
стоимость которого ограничена величиной А: .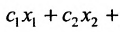

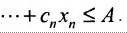Например, пусть;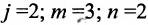

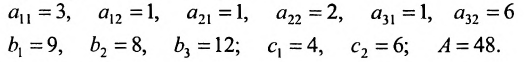
Тогда получаем систему:

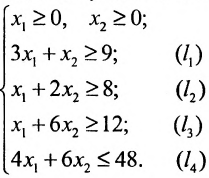
Определим множество решений данной системы на плоскости . Вначале строим граничные прямые

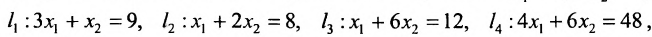
(рис. 8.4) соответствующие данным неравенствам. Каждая из них делит плоскость на две полуплоскости, одна из которых является решением соответствующего неравенства. Для выбора полуплоски являющейся решением неравенства, подставляем в каждое неравенство.

Если получаем верное неравенство, то полуплоскость, содержащая начало координат, является решением неравенства, в противном случае - полуплоскость, не содержащая начало координат, является решением неравенства.

Стрелки на прямых указывают полуплоскости, являющиеся областями решений данных неравенств. Заштрихованный четырехугольник 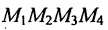и определяет все возможные рационы 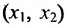для кормления скота, удовлетворяющие данным условиям.