Плоскость на эпюре Монжа в начертательной геометрии с примерами

Плоскость на эпюре Монжа:

Плоскость на эпюре может быть задана шестью способами: тремя точками, не лежащих на одной прямой; прямой и точкой, не лежащей на прямой; двумя параллельными прямыми; двумя пересекающимися прямыми; любой плоской фигурой и следами (рисунок 3.1).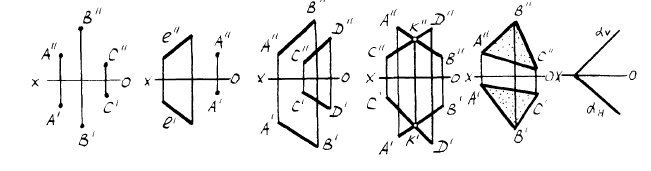

Плоскости аналогично прямым делятся на плоскости общего и частного положения. На рисунке 3.2 представлены пространственные чертежи плоскостей.

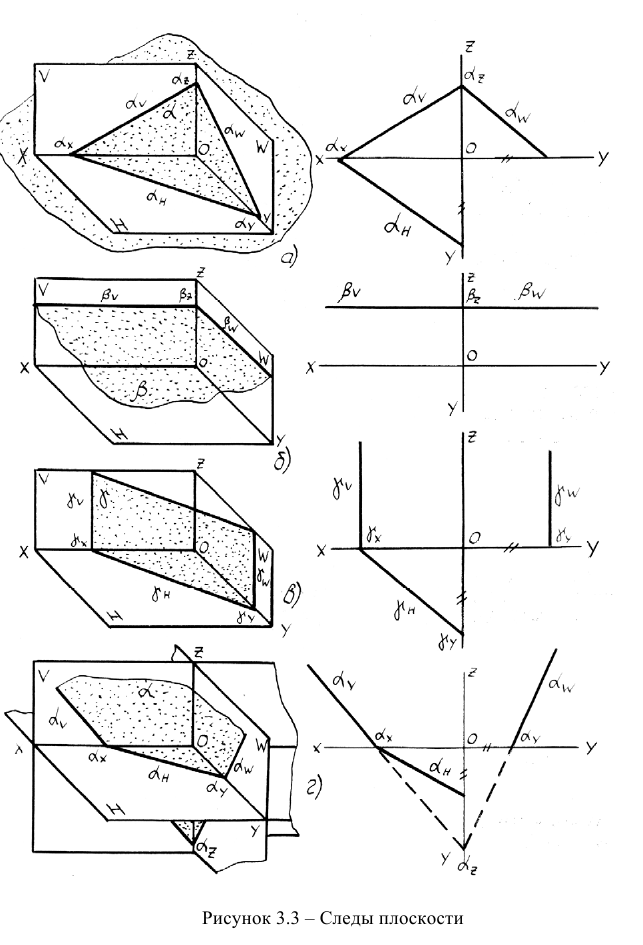
У проецирующих плоскостей два следа всегда перпендикулярны осям. Третий след наклонен к соответствующей оси и называется собирательным следом. Он называется так потому, что, если в плоскости находится какой-либо геометрический объект (точка, прямая или кривая линия, треугольник и т.д.), то он проецируется на этот след в линию, совпадающую со следом (след "собирает" на себя проекцию объекта).

У плоскостей, параллельных плоскостям проекций, один след отсутствует, а два других следа являются продолжением друг друга и параллельны соответствующим осям проекций.

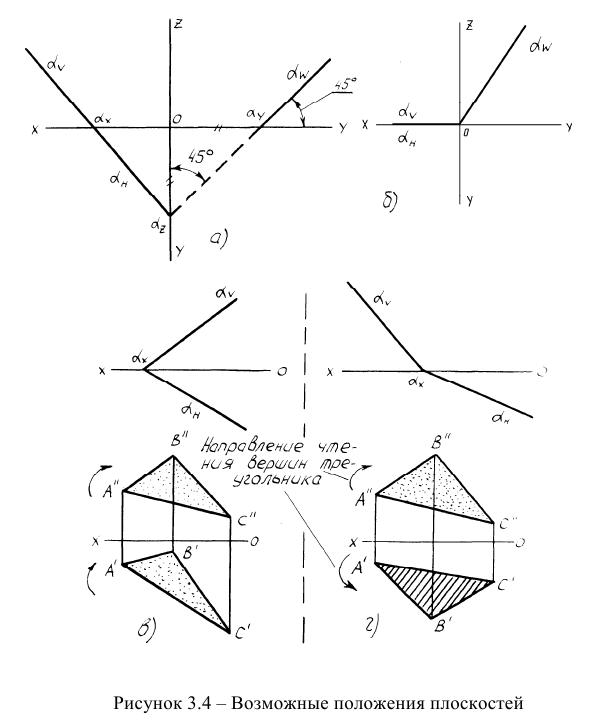
Если плоскость в пространстве равнонаклонена к какой-либо паре плоскостей проекций, то следы такой плоскости вырождаются в прямую линию (рисунок 3.4а).

Плоскости, перпендикулярные к одной из плоскостей проекций и проходящие через ось проекций, называются осевыми плоскостями. Два их следа сливаются с соответствующими осями (рисунок 3.46).

Плоскости общего положения дополнительно делятся на плоскости с односторонней (рисунок 3.4в) и двухсторонней (рисунок 3.4г) видимостью. Признаком односторонней видимости является, например, одинаковое направление чтения букв вершин треугольника на проекциях.

Главные линии плоскости

Главные линии плоскости делятся на линии уровня и линии наибольшего наклона.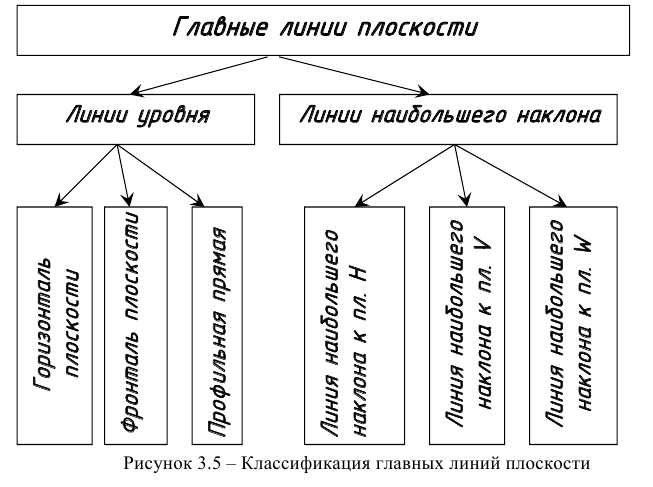

Классификация главных линий плоскости представлена на рисунке 3.5, а на рисунке 3.6 - их наглядное изображение.

К линиям уровня относятся горизонталь, фронталь и профильная прямая плоскости. Они принадлежат плоскости и проводятся в ней по тем же правилам, что и обычные прямые. В каждой плоскости можно провести бесчисленное множество линий уровня. На рисунке 3.7 показано проведение горизонтали и фронтали в плоскостях, заданных плоской фигурой и следами.

При проведении горизонтали и фронтали в плоскости, заданной треугольником, целесообразно взять одну из вершин треугольника за точку, принадлежащую плоскости, и строить проекции h и f из этой вершины, что упрощает построения.

• Заказать чертежи

В плоскости, заданной следами, горизонталь проводится параллельно горизонтальному следу, а фронталь - фронтальному следу.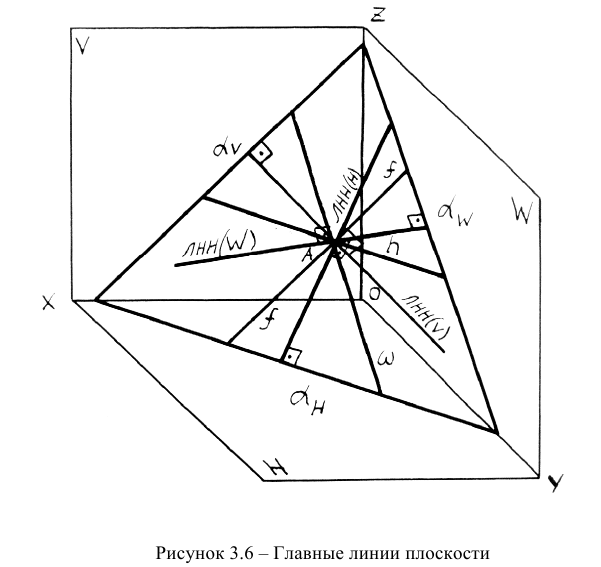

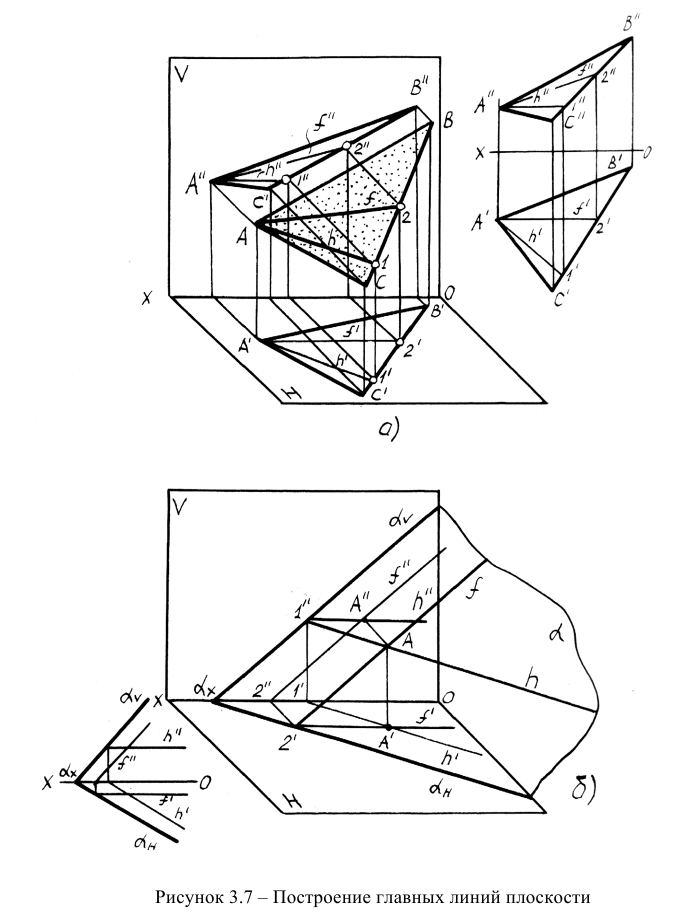
В обоих случаях построение горизонтали начинают с фронтальной проекции, а построение фронтали - с горизонтальной проекции, так как они параллельны оси ОХ.

Линиями наибольшего наклона плоскости к плоскостям проекций (ЛНН) называются линии, проведенные в плоскости и определяющие наибольший угол между плоскостью и плоскостью проекций, т.е. величину образованного двугранного угла. Различают линию наибольшего наклона плоскости к плоскости проекций Н - ЛНН(Н), к плоскости проекций V -ЛНН(V) и к плоскости проекций W - ЛНН(W). Рассмотрим подробнее первые две линии.

Линия наибольшего наклона плоскости к плоскости проекций Н проводится перпендикулярно к горизонтальному следу плоскости или к горизонтали плоскости. Линия наибольшего наклона плоскости к плоскости проекций V проводится перпендикулярно к фронтальному следу плоскости или к фронтали (рисунок 3.8).

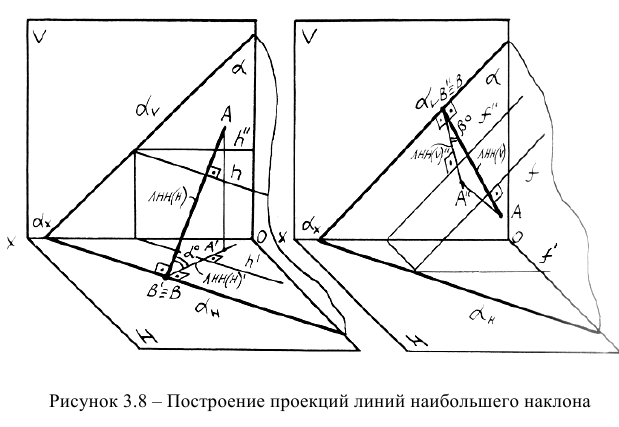
Принцип методики построения проекций ЛНН основывается на теореме прямого угла: если один из катетов прямого угла параллелен какой-либо плоскости, то на эту плоскость прямой угол проецируется в натуральную величину (см. рисунок 2.8).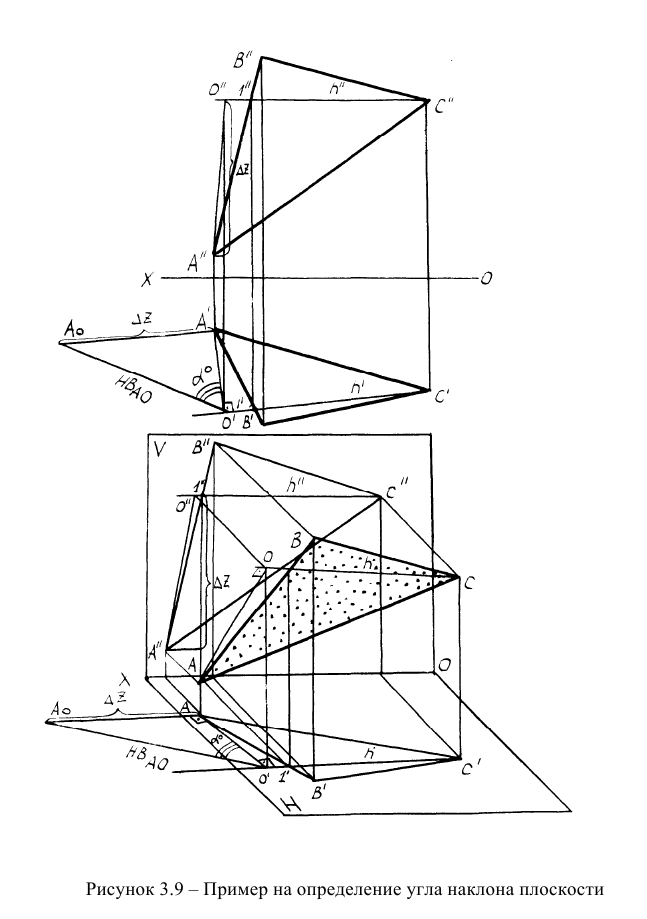

Исходя из пространственных моделей в соответствие с рисунком 3.8 и на основании теоремы о проецировании прямого угла, можно сформулировать методику построения проекций ЛНН(Н) и JIHH(V): горизонтальная проекция ЛНН(Н) проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу, а фронтальная проекция ЛНН(V) - перпендикулярно фронтальной проекции фронтали или фронтальному следу. Алгоритмически это может записано в следующем виде: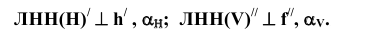

Проекции 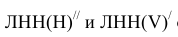образуются по ходу построений.

Угол наклона плоскости к плоскости проекций Н (угол 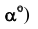определится как угол между натуральной величиной ЛНН(Н) и её горизонтальной проекцией, а угол наклона плоскости к плоскости проекций У (угол 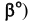- как угол между натуральной величиной ЛНН(V) и её фронтальной проекцией.

Пример: Определить угол наклона плоскости ЛВС к плоскости проекций Н (рисунок 3.9).

Решение: Для определения угла 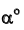в плоскости треугольника AВС необходимо провести ЛНН(Н), которая проводится перпендикулярно горизонтали. В связи с этим проведем в плоскости горизонталь h (проекции 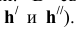Далее из точки С' под прямым углом к 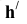проведем горизонтальную проекцию ЛНН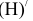 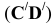и построим фронтальную проекцию ЛНН(Н) (C"D" ). Затем методом прямоугольного треугольника найдем натуральную величину ЛНН(Н) 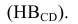Угол а° между 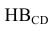и горизонтальной проекцией линии наибольшего наклона 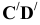- искомый. Задача на рисунке 3.9 представлена в пространственной и эпюрной формах.