Плоскость - определение, виды и правила с примерами

Содержание:

Всякая поверхность в пространстве задается в декартовых координатах уравнением вида F(x, у, z)= 0.

Если F(х9 у, z) - многочлен n -й степени, то соответствующая поверхность называется алгебраической поверхностью n-го порядка или просто поверхностью n-го порядка.

Всякая поверхность 1-го порядка есть плоскость, т.е. всякое уравнение 1-й степени:

Ax + By + Cz + D = 0 (6.1)

определяет плоскость. Уравнение (6.1) называется общим уравнением плоскости.

Вектор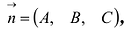

Этот факт будет постоянно использоваться в дальнейшем. Вектор n называют нормальным вектором плоскости (6.1).

Уравнение плоскости, проходящей через данную точку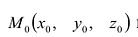

Очевидно, что уравнение (6.1) имеет смысл только тогда, когда хотя бы один из коэффициентов А, В, С не равен нулю.

Рассмотрим частные случаи.

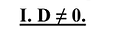
1. Если A = 0, то уравнение By + Cz + D = 0 определяет плоскость, параллельную оси Ох, так как вектор нормали к этой плоскости 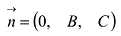перпендикулярен оси Ох (проекция ненулевого вектора на ось равна нулю тогда, когда он перпендикулярен этой оси).
2. Аналогично, если В = 0, то уравнение Ax + Cz + D = 0 определяет плоскость, параллельную оси Оу.
3. Если С = 0. То уравнение Ax + By + D = 0 определяет плоскость, параллельную оси Oz.
4. Если А = B = 0, то уравнение Cz + D = 0 или 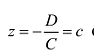определяет плоскость, параллельную плоскости хОу. В этом случае вектор нормали п = (о, 0, с) перпендикулярен к осям Од- и Оу, т.е. к плоскости хОу.
5. При A = С = 0 имеем By + D=0 или 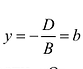- уравнение плоскости, параллельной координатной плоскости xOz.
6. Если B = С = 0, то уравнение Ax+D = 0 или 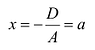определяет плоскость, параллельную плоскости yOz.

II. D = 0.

1. Если D = 0, то уравнение Ax + By + Cz = 0 определяет плоскость, проходящую через начало координат, так как координаты точки O (0, 0, 0) удовлетворяют этому уравнению.
2. Если A = D = 0, то уравнение By+ Cz = 0 определяет плоскость, вектор нормали которой 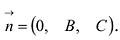. Эта плоскость проходит через ось Ох.
3. Аналогично, если B = D = 0, то уравнение Ax + Cz = 0 определяет плоскость, проходящую через ось Оу.
4. Если C = D = 0, то уравнение Ах + By = 0 определяет плоскость, проходящую через ось Oz.
5. Если A = B = D = 0, то уравнение Cz = 0 или 2 = 0 определяет плоскость хОу. Аналогично, уравнения x = 0 и у = 0 определяют соответственно плоскости yOz и xOz.

Если в уравнении (6.1) все коэффициенты А, B, С, D отличны от нуля, то это уравнение может быть преобразовано к уравнению плоскости в отрезках:

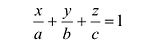(6.3)

Здесь а, b, с - величины отрезков, отсекаемых плоскостью на осях координат.

Нормальное уравнение плоскости

Нормальным уравнением плоскости называется уравнение: 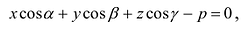(6.4)

где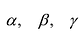 - углы между перпендикуляром, опущенным из начала координат на плоскость, и положительным направлением осей координат, а p- расстояние от плоскости до начала координат.

Нормальное уравнение отличается от общего уравнения тем, что в нем коэффициенты при x, у, z являются координатами единичного вектора 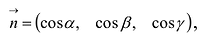перпендикулярного плоскости, а свободный член - отрицательный.

Общее уравнение (1) приводится к нормальному виду умножением его на нормирующий множитель 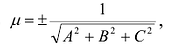при этом знак выбирается противоположным знаку свободного члена D (если D = 0, знак можно выбрать любой).

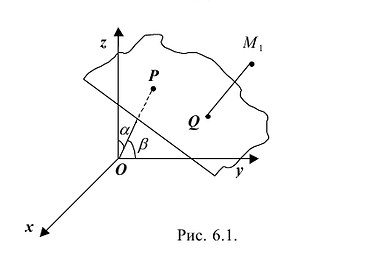
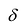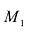Отклонением точки , от плоскости называется ее расстояние d от плоскости, взятое со знаком плюс, если точка 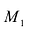и начало координат О лежат по разные стороны от плоскости (Рис. 6.1), и со знаком минус - если 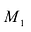и О лежат по одну сторону от плоскости.

Отклонение точки 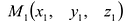от плоскости определяется по формуле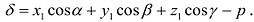

Следовательно, чтобы найти расстояние от точки до плоскости, надо привести уравнение плоскости к нормальному виду и в его левую часть вместо х, у, z подставить координаты точки 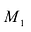. Получим отклонение 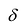. А расстояние .

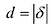Взаимное расположение плоскостей

Пусть даны плоскост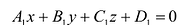и и 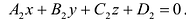. Угол между ними равен углу между перпендикулярными к ним векторам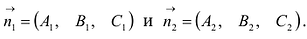

Косинус этого угла вычисляется по формуле:

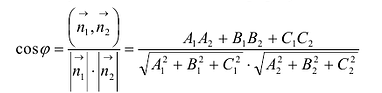(6.5)

Плоскости параллельны, если 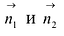коллинеарны, т.е.:

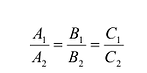(6.6) Условие перпендикулярности плоскостей -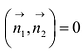, т.е.

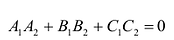(6.7)

Если даны три плоскости:

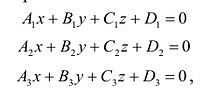(6.8)

, то их общие точки определяются системой уравнений (6.8).

В случае, если перпендикулярные этим плоскостям векторы

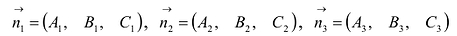некомпланарны, три плоскости имеют единственную общую точку.

В самом деле, тогда смешанное произведение

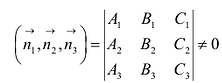
а записанный определитель является определителем системы уравнений (6.8), и, следовательно, система (6.8) имеет единственное решение.

Плоскость в высшей математике

Плоскость в пространстве также можно задать разными способами (тремя точками; точкой и вектором, перпендикулярным плоскости). В зависимости от этого рассматриваются различные виды ее уравнений.

1. В пространстве Oxyz составим уравнение плоскости Р, проходящей через точку 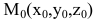перпендикулярно вектору n=(А,В,С) (нормальному вектору плоскости) (рис.9). Рис.9

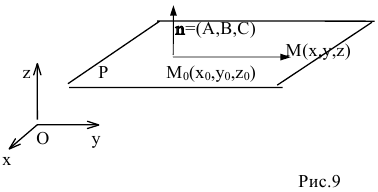
Возьмем любую точку M(x,y,z), лежащую на плоскости, и рассмотрим вектор 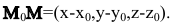Так как векторы 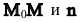являются взаимно перпендикулярными, их скалярное произведение равно нулю:

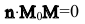
или в координатной форме:

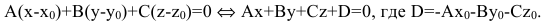
Уравнение Ax+By+Cz+D=0, где А, В и С не равны одновременно нулю 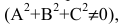называется общим уравнением плоскости.

2. Составим уравнение плоскости, проходящей через три точки 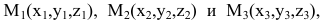не лежащие на одной прямой. Пусть M(x,y,z) - произвольная точка этой плоскости. Рассмотрим векторы

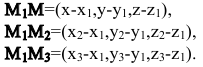
Эти векторы компланарны, поэтому их смешанное произведение равно нулю: 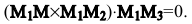Условие компланарности трех векторов в координатной форме запишется так: 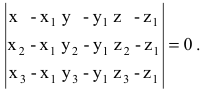Это и есть искомое уравнение плоскости.

Задачи на прямую и плоскость

Прямая как пересечение двух плоскостей

Рассмотрим две непараллельные плоскости, заданные общими уравнениями. В этом случае плоскости пересекаются по прямой, определяемой уравнениями

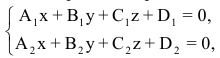
которые называются общими уравнениями прямой.

Замечание. Одна и та же прямая может быть задана различными системами двух линейных уравнений, т.к. через одну прямую можно провести бесчисленное множество плоскостей.

Пример №1

Общие уравнения прямой привести к каноническому виду:

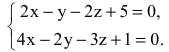
Решение:

Векторы 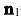=(2,-1,-2) и 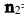=(4,-2,-3) являются нормальными векторами плоскостей. Направляющий вектор прямой можно вычислить по формуле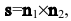

т.к. он принадлежит обеим плоскостям и, следовательно, удовлетворяет условиям:

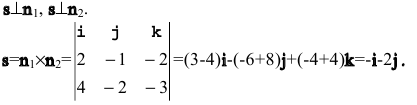Найдем точку на прямой. Положив в общих уравнениях, например, х=0, получим систему уравнений:

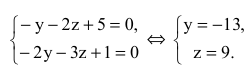
По точке на прямой (0,-13,9) и направляющему вектору s=(-l,-2,0) составим канонические уравнения прямой:

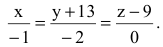Т.к. деление на нуль невозможно, то уравнения прямой примут вид:

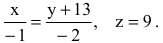Задача решена.

Расстояние от точки до прямой на плоскости

Пусть заданы прямая на плоскости своим общим уравнением Ах+Ву+С=0 и точка 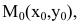не лежащая на этой прямой.

Найдем расстояние d от точки до данной прямой. Проведем из точки 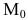перпендикуляр 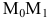на прямую l (рис. 10).

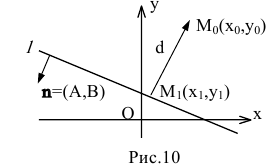
Искомое расстояние d есть модуль вектора 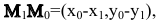который коллинеарен вектору n=(А,В). Из определения скалярного произведения следует: 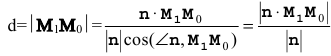или в координатной форме:

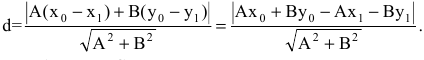А так как 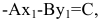то

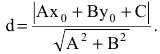
Аналогично находится расстояние от точки до плоскости. Если заданы плоскость своим общим уравнением Ax+By+Cz+D=0 и точка 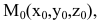не принадлежащая этой плоскости, то расстояние d от точки до плоскости находится по формуле:

• Заказать решение задач по высшей математике

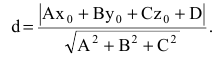
Пример №2

Вершины треугольной пирамиды находятся в точках А( 1,1 ,-1), В(2,1,-3), С(-1,1,1) и D(0,7,3). Вычислить высоту пирамиды, опущенную из вершины D на основание АВС.

Решение:

Искомая высота есть расстояние от точки D до плоскости АВС. Составим уравнение плоскости, проходящей через три точки А, В и С. Возьмем любую точку M(x,y,z), принадлежащую этой плоскости. Тогда векторы АМ=(х-l,y-l,z+l), АВ=(1,0,-2) и АС=(-2,0,2) будут лежать в плоскости АВС и, следовательно, их смешанное произведение будет равно нулю:

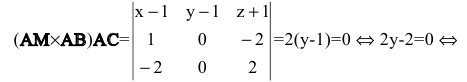
у-1=0 - общее уравнение плоскости АВС. Применяя формулу расстояния от точки до плоскости, получим

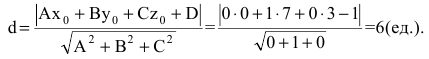
Задача решена.

Пусть 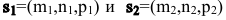- направляющие векторы двух прямых в пространстве. Угол между двумя прямыми есть угол между их направляющими векторами, т.е.

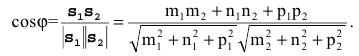
Условие параллельности двух прямых: 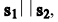т.е.

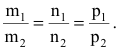Условие перпендикулярности двух прямых: 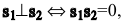т е-

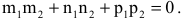
Пусть 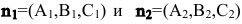- нормальные векторы двух плоскостей в пространстве. Угол между двумя плоскостями есть угол между их нормальными векторами, т.е.

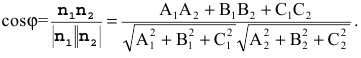
Условие параллельности двух плоскостей: 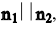- т.е.

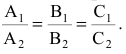
Условие перпендикулярности двух плоскостей: 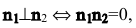т.е.

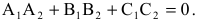
Пусть прямая l задана каноническими уравнениями

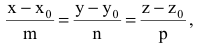
а плоскость Р - общим уравнением

Ax+By+Cz+D=0.

Углом между прямой и плоскостью называется острый угол между пря-мои и ее проекцией на плоскость. Он является дополнительным до 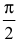к углу между векторами 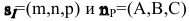(рис.11):

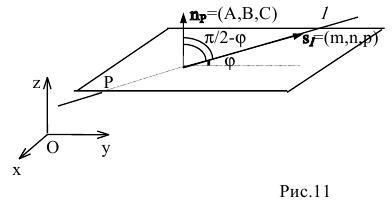
Тогда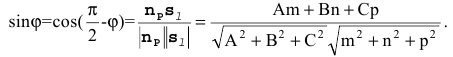

Условие перпендикулярности прямой и плоскости: 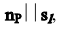т.е.

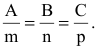
Условие параллельности прямой и плоскости: 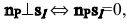т.е. Am+Bn+Cp=0.