Плоско-параллельное движение твердого тела в теоретической механике

Плоско-параллельное движение твердого тела:

Плоско-параллельным или плоским называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных данной неподвижной плоскости.

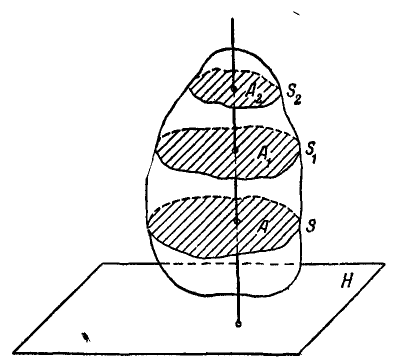
Рис. 171.

Пусть неподвижная плоскость Н и тело А совершают плоское движение (рис. 171). Рассекая это тело плоскостями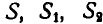

Отсюда следует, что при изучении плоского движения тела достаточно изучить движение некоторой плоской фигуры, взятой в теле параллельно неподвижной плоскости, движущейся в своей плоскости (рис. 172). Выберем на подвижной фигуре любую точку О (полюс); тогда при движении фигуры полюс будет описывать некоторую кривую.

Рис.172.

Если бы все точки плоской фигуры двигались так же, как и выбранная нами точка О, то движение фигуры было бы поступательным. В общем, же случае движение плоской фигуры S можно рассматривать как поступательное движение вместе с полюсом О и в то же время делающей поворот вокруг О.

Если через полюс О провести две любые прямые, 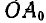и 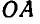(рис. 172), из которых прямая  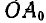все время остается горизонтальной, а прямая ОА, связанная с фигурой S, совершит поворот вместе с ней, то положение подвижной фигуры в данный момент вполне определится тремя величинами — координатами х и у полюса О и углом поворота 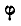прямой ОА. Координаты х, у и 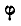, определяющие положение фигуры S, меняются с течением времени, а поэтому являются функциями времени:

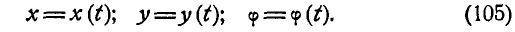
Уравнения (105) называются уравнениями плоско-параллельного движения.

Покажем, что при изучении движения подвижной фигуры достаточно изучить движение двух каких-либо ее точек. Пусть фигура из положения I перейдет в положение II (рис. 173).

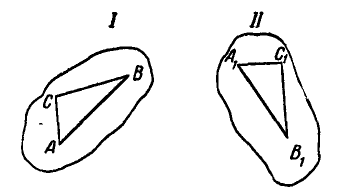
Рис. 173.

Тогда взятые на ней точки А и В, переместившись вместе с фигурой, займут в новом положении II фигуры места 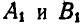 , т. е. отрезок АВ переместится в положение 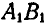. Нетрудно видеть, что при этом может быть определено и новое положение любой точки С фигуры путем построения треугольника 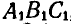, равного треугольнику ABC.

Отсюда следует, что для исследования движения подвижной плоскости по неподвижной достаточно.исследовать движение отрезка, принадлежащего к подвижной плоскости.

Пусть прямая АВ, принадлежащая к подвижной фигуре, переместится при своем движении в положение 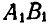(рис. 174). 

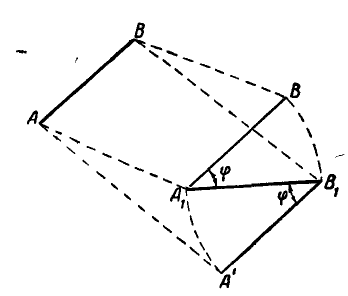
Рис. 174.

Если за полюс принять точку А, то это перемещение можно представить как поступательное движение отрезка вместе с полюсом А в положение 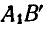и затем поворот отрезка вокруг полюса в положение 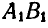на угол 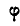. Если бы в качестве полюса мы выбрали точку В, то отрезок АВ следовадс бы сначала переместить поступательно в положение 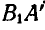, а затем повернуть на угол 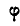вокруг выбранного полюса .

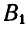Таким образом, перемещение отрезка может быть выполнено при помощи двух операций: параллельного переноса до совпадения одной из точек с ее конечным положением и поворота около этой точки до совпадения отрезка с требуемым положением. Независимо от того, какой из концов отрезка А или В выбран нами за полюс, поворот отрезков 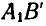йли 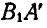вокруг выбранного полюса до совмещения с заданным положением 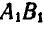следует производить в обоих случаях на один и тот угол .

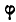В нашем случае поворот отрезка на угол 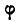происходит по. часовой стрелке по отношению к полюсу. Отсюда следует, что при движении подвижной фигуры ее угол поворота, а следовательно, и угловая скорость не зависят от выбора полюса.

Докажем теперь следующую теорему Эйлера.

Всякое непоступательное перемещение плоской фигуры в ее плоскости можно осуществить путем вращения вокруг некоторого центра.

Пусть фигура вместе с прямой АВ переместится в положение 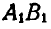(рис. 175). Соединим точк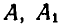и и 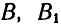и из середин отрезков 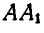и 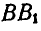восстановим перпендикуляры до пересечения их в точке О.

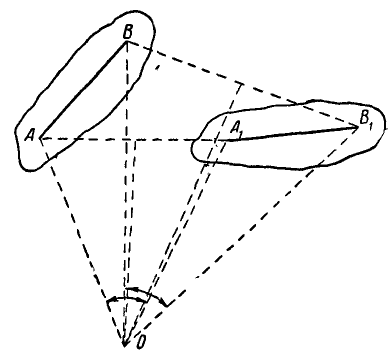
Рис. 175.

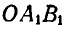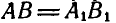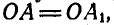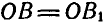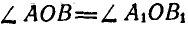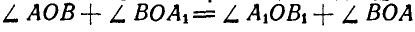Полученные треугольники ОАВ и равны между собой, так как в силу неизменяемости фигуры и  а также по построению; отсюда: или , откуда

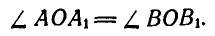
Если мы повернем отрезок АВ вокруг точки О на угол 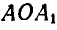, равный углу 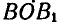, то ОА совпадет с 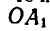, и ОВ совпадет с 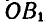, в силу равенства этих углов, и отрезок АВ займет положение 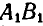, что и доказывает, теорему Эйлера.

Переходя к изучению плоского движения как непрерывного процесса, рассматриваем его состоящим из бесконечно большого числа бесконечно малых элементарных перемещений.

Применяя к каждому из них теорему Эйлера, приходим к заключению, что плоское движение может быть рассматриваемо в пределе, как непрерывный ряд бесконечно малых вращений около различных центров, которые называются полюсами мгновенных вращений или мгновенными центрами вращения.

Мы уже знаем, что движение плоскости можно рассматривать как сложное, состоящее из поступательного движения вместе с полюсом и из вращательного — около полюса. Если бы полюс А (рис. 176) был неподвижным, то скорость любой точки В  фигуры определилась бы как вращательная по отношению к точке А по формуле (89):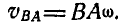

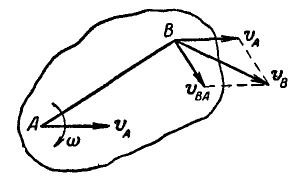
Рис. 176.

В общем же случае скорость полюса А (произвольно выбранной нами точки) не равна нулю, а поэтому к вращательной скорости точки В по отношению к А присоединится еще и скорость 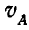поступательного движения фигуры вместе с полюсом А.

Полная скорость точки В получится как сумма двух скоростей: скорости точки А и скорости точки В по отношению к полюсу А. Складывая эти скорости как векторы по правилу параллелограмма, находим:    

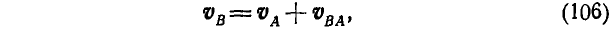
или

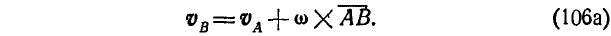
Проектируя обе'части векторного равенства (106) на направление АВ и замечая, что 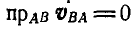ввиду перпендикулярности вектора 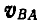к АВ, найдем, что  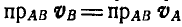 т. е. проекции скоростей двух точек твердого тела на направление прямой, соединяющей эти точки, равны, между собой и направлены в одну сторону.

Покажем теперь, что при непоступательном движении плоской фигуры существует точка этой фигуры, скорость которой в данный момент равна нулю. Эта точка называется мгновенным центром скоростей и, как было отмечено выше, расположена на самой подвижной плоскости.

Та же точка неподвижной плоскости, с которой в данный момент совпадает мгновенный центр скоростей, называется мгновенным центром вращения, или полюсом мгновенного вращения. Очевидно, что положения мгновенных центров скоростей и мгновенных центров вращения при движении плоской фигуры по неподвижной плоскости будут непрерывно меняться.

Допустим, что некоторая подвижная плоскость движется по неподвижной плоскости.

Вместо подвижной плоскости рассмотрим движение отрезка АВ, принадлежащего этой плоскости (рис. 177). Обозначим мгновенную угловую скорость отрезка 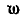и, приняв точку А за полюс, построим вращательную скорость 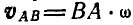точки В вокруг полюса А, отложив ее перпендикулярно к прямой ВА. Соединив полюс А с концом М скорости  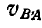, заключаем, что концы вращательных скоростей всех точек отрезка АВ будут расположены на прямой AM ввиду того, что скорости эти пропорциональны расстояниям точек от полюса А. Если скорость 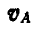полюса А нам известна, то полная скорость точки В найдется по формуле (106), для чего к вектору 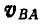следует прибавить вектор .

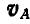Легко видеть, что концы векторов, изображающих полные скорости точек прямой АВ (или ее продолжения), лягут на прямой KN, параллельной АМ ; например, скорость точки С изобразится вектором СТ. Однако движение плоскости мы могли бы задать каким-либо другим отрезком АЕ, составляющим, например, с вектором 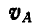скорости полюса А угол 90°. Построив вращательную скорость точки Е вокруг полюса А в виде вектора 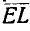, отложенного в том же масштабе, что и вращательные скорости точек В и С, проведем из конца вектора 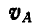прямую KD || AL.

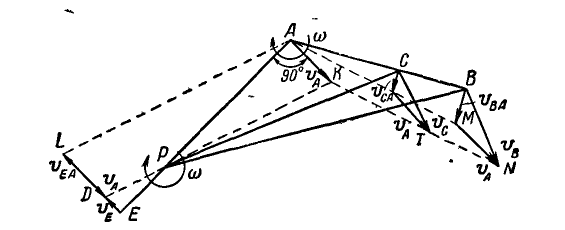
Рис. 177.

По предыдущему заключаем, что концы векторов полных скоростей точек отрезка АЕ должны лежать на прямой DK. Тогда полная скорость точки Е изобразится вектором 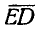В пересечении же прямых АЕ и KD получается точка Р, скорость которой равна в данный момент нулю; эта точка, как было указано выше, называется мгновенным центром скоростей, а совпадающая с ней точка на неподвижной плоскости — мгновенным центром вращения, или полюсом мгновенного вращения.

Мгновенный центр скоростей не следует смешивать с другими точками подвижной плоскости, в частности с полюсами. Эта неподвижная точка фигуры для данного момента только одна, тогда как в качестве полюсов, вообще говоря, могут быть выбраны любые точки фигуры. Выбирая в качестве полюса точку Р—мгновенный центр скоростей, найдем по формуле (106,а), например, скорость точки В:    

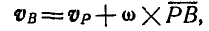
но так как 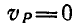, то 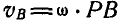, и мы приходим к формуле (89).

Отсюда следует, что скорости всех точек плоской фигуры пропорциональны их расстояниям до мгновенного центра вращения (так называемым мгновенным радиусам) и перпендикулярны к этим радиусам.

Для нахождения положения мгновенного центра вращения достаточно знать вид траекторий двух точек плоской фигуры. Пусть, например, отрезок АВ, принадлежащий этой фигуре, перемещается так, что точка А его движется по траектории 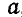, а точка В по траектории b (рис. 178). Тогда мгновенный центр вращения отрезка АВ в данный момент будет находиться в точке Р пересечения нормалей к траекториям точек А к В отрезка АВ, так как направлены по касательным к их траекториям.

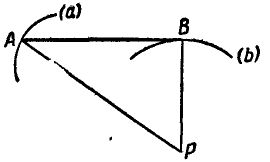
Рис. 178.

Задача №1

Найти построением мгновенный центр Р отрезка АВ в следующих случаях:

1) линейки АВ, могущей перемещаться своими концами А и В по сторонам угла АСВ (рис. 179, а);

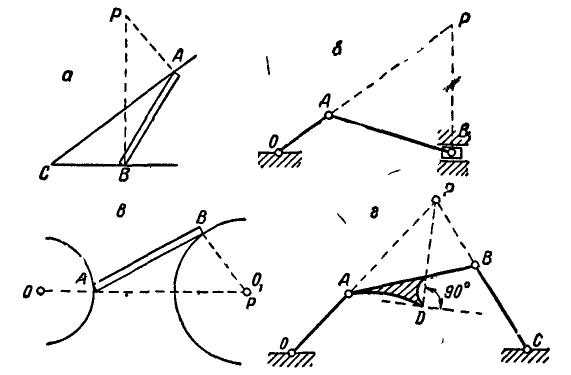
Рис. 179.

2)    шатуна АВ кривошипно-шатунного механизма (рис.. 179, б);

3)    линейки АВ, могущей перемещаться своими концами А и В по направляющим двух кругов с центрам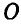и и 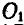(рис. 179, в);

4)    шатуна АВ шарнирного четырехзвенника ОABC (рис. 179, г).

Найти также направление линии, вдоль которой направлена скорость точки D конца прилива шатуна АВ.

Указание: полюс мгновенного вращения Р найдется для всех случаев на пересечении нормалей к траекториям точек А и В. Линию, вдоль которой направлена скорость точки D (рис. 179, г), найдем, если соединим точку D с полюсом-мгновенного вращения Р и проведем через точку D прямую, перпендикулярную к направлению мгновенного радиуса PD.

Задача №2

Определить построением ту точку М шатуна АВ кривошипно-шатунного механизма; скорость которой направлена вдоль шатуна АВ, а также найти величину этой скорости (рис. 180), Длина кривошипа 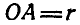и угловая скорость его вращения .

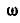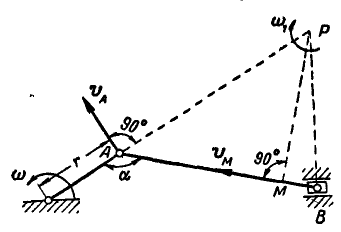
Рис. 180.

Решение. Найдем полюс Р мгновенного вращения шатуна АВ; он находится на пересечении нормалей к траекториям точек А и В. Опуская из .точки Р перпендикуляр на направление шатуна АВ, получим ту точку М, скорость которой направлена вдоль шатуна АВ.

Если мы обозначим мгновенную угловую скорость вращения шатуна АВ вокруг мгновенного центра Р через 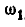, то линейная скорость точки М, согласно формуле (89), будет:

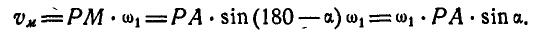
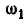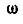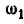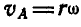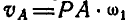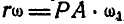Для определения мгновенной угловой скорости выразим линейную скорость точки А через угловые скорости и ; ; с другой стороны: или , откуда

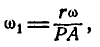
а поэтому

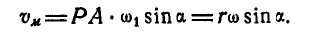
Задача №3

Показать, что при качении без скольжения подвижной фигуры 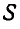по неподвижной кривой MN (рис. 181) мгновенный центр подвижной фигуры находится в точке касания катящегося периметра и неподвижной кривой.

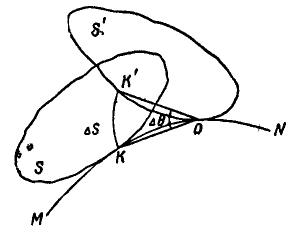
Рис. 181.

Решение. Пусть катящаяся фигура в моменты 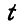 и 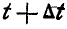 занимает положения 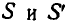; в момент t точкой касания подвижной и неподвижной кривых является точка К, а в момент 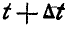— точка О. Покажем, что скорость точки К равна нулю. В самом деле, принимая приближенно дугу КК', которую опишет точка К за время М, за дугу окружности, имеем:

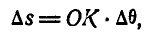
или

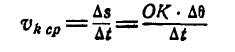
и

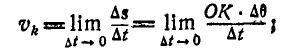
при

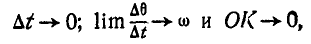
а отсюда скорость 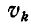точки 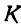в данный момент равна нулю.

Задача №4

Колесо автомобиля радиусом R= 40 см катится без скольжения по неподвижной прямой так, что скорость его центра 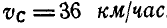. Найти величины и исправления скоростей точек А и В обода колеса, лежащих на горизонтальном и вертикальном диаметрах колеса (рис. 182).

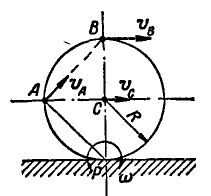
Рис. 182.

Решение. Так как полюс мгновенного вращения колеса находится в точке Р касания колеса с прямой, то скорости 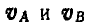точек А и В будут перпендикулярны к их мгновенным радиусам РА и РВ. Угловая скорость мгновенного вращения;

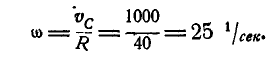
Величины же скоростей точек А и В найдутся по формуле (89):

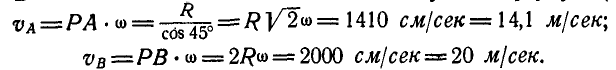
Задача №5

Кривошипы ОС и 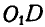шарнирного четырехзвенника 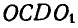(рис. 184),    представляющего собой шарнирный параллелограмм, вращаются с постоянной угловой скоростью 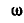. Внутри четырехзвенника имеется звено АВ, которое соединено в точке В шарнирно с звеном CD, а в точке А —с ползуном, могущим перемещаться по неподвижной прямой 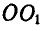. Для положения механизма, показанного на чертеже, определить скорости точек В и А, если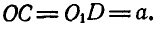

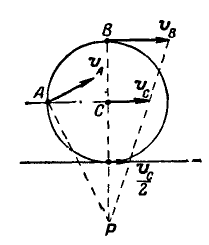
Рис. 183.

Решение. Мгновенный центр звена CD находится в бесконечности, так как кривошипы ОС и 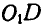параллельны.

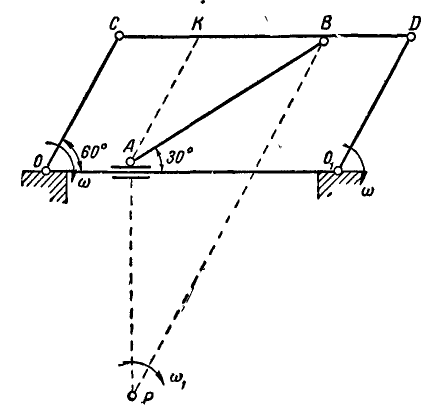
Рис. 184.

Отсюда заключаем, что звено CD движется поступательно. Для нахождения мгновенного центра звена АВ проведем нормали к траекриям точек А и В, т. е. 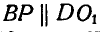 и 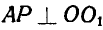; в пересечении их получим точку Р, которая является полюсом мгновенного вращения звена АВ. Обозначив мгновенную угловую скорость вращения звена АВ вокруг Р через 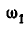, по формуле (89) найдем скорости точек А и В:

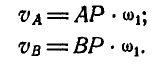
Проведя 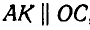, найдем из треугольников АКВ и ABP величины мгновенных радиусов РА и РВ:

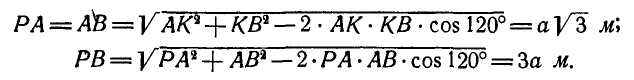
Величина мгновенной угловой скорости 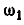 определится из условия, что звено CD движется поступательно, а поэтому 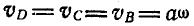; с другой стороны: 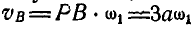. Следовательно,  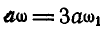, откуда .

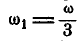Скорость же точки А:

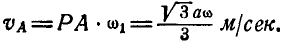
Задача №6

Найти скорость и ускорение ползуна В кривошипно-шатунного механизма ОАВ (рис. 185), если длины шатуна и кривошипа одинаковы: 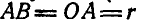 и кривошип OA вращается с постоянной угловой скоростью .

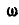Найти также угловую скорость 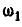шатуна АВ и скорость средней его точки М при четырех положениях кривошипа, для которых угол АОВ соответственно равен: .

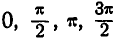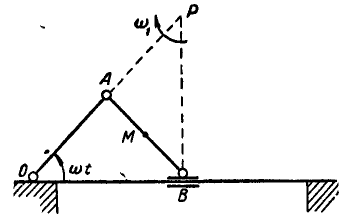
Рис. 185.    

Решение. Полюс Р мгновенного вращения шатуна АВ найдется в пересечении прямых OA и . Так как ОА=АР, то и скорость точки В найдется по формуле (89):

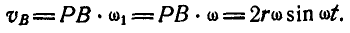
Точка В движется прямолинейно, поэтому она обладает только касательным ускорением:

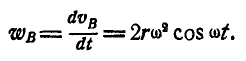
При 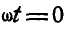мгновенный центр шатуна находится в точке В, а угловая скорость шатуна ; скорость же точки М:

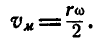
При 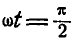 мгновенный центр шатуна находится в бесконечности; в этом случае шатун движется поступательно, его мгновенная угловая скорость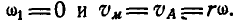

При 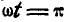мгновенный центр шатуна находится опять в точке В, но при этом его мгновенное вращение будет происходить вокруг В также по часовой стрелке, поэтому: .

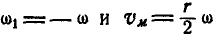При 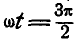 шатун движется поступательно, его мгновенная угловая скорость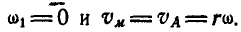

Задача №7

Двухповодковая группа состоит из двух стержней AM и MB, соединенных между собой шарниром М (рис. 186). Зная скорост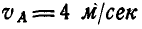и и 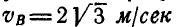точек А к В, построить на чертеже скорость 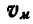точки М. Угол AMВ  равен 60°.

Решение. Скорость точки М найдется из условия, что проекции скорости точки М на направления AM и ВМ соответственно равны проекциям скоростей точек А и В на те же направления. Перенося проекции скоростей точек А и В на направления AM и ВМ в точку М, восстановим из концов проекций скоростей перпендикуляры до взаимного их пересечения и, соединив эту точку с точкой М, получим вектор скорости 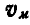точки М. Величина этого вектора найдется на основании простых вычислений.

Ответ: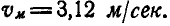

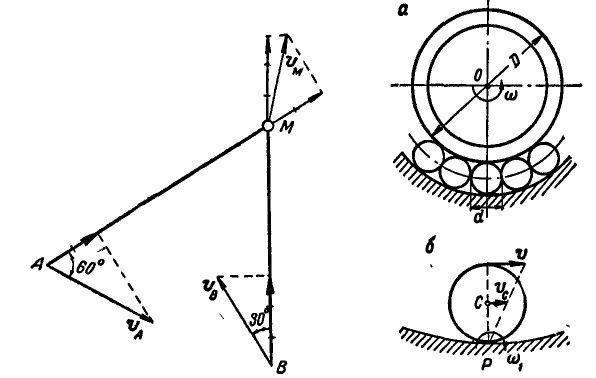
              Рис. 186.                                                    Рис. 187.

Задача №8

Шариковый подшипник достоит из внутреннего кольца диаметра D, вращающегося с угловой скоростью 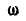вокруг оси, проходящей через его центр О перпендикулярно плоскости чертежа, и шариков, катящихся без скольжения ,по неподвижной втулке (рис. 187, а). Найти величину линейной скорости центра одного из шариков и его угловую скорость, если диаметр шарика равен d.

Решение. Окружная скорость кольца равна 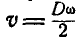; этой же скоростью обладает и точка касания каждого из шариков с кольцом (рис. 187, б). Так как полюс мгновенного вращения шарика находится в точке Р —касания его с неподвижной втулкой, то отсюда заключаем, что 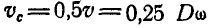и угловая скорость вращения шарика: 

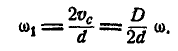
Задача №9

Две параллельные рейки АВ и CD (рис. 188) движутся в противоположные стороны с постоянными скоростями

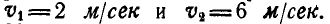
Между рейками находится диск радиуса 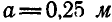. Вследствие движения реек и трения диск катится по рейкам без скольжения,

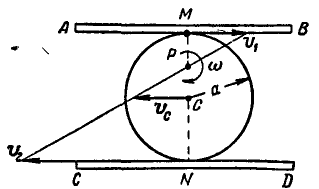
Рис. 188.
 

так что скорости точек М и N касания его с рейками соответственно равны 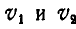. Определить скорость 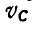центра С диска и угловую скорость 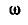его вращения.

Решение. Диск совершает плоско-параллельное движение. Полюс мгновенного вращения его Р находится на пересечении прямой, соединяющей концы векторов скоростей 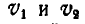и прямой, проходящей через точки М и N касания диска с рейками.

Для определения положения точки Р имеем два уравнении

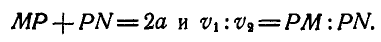
Отсюда находим, что РМ=0,5а и, следовательно, .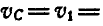

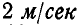Угловая скорость вращения диска определится из равенства 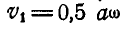, откуда:

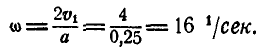
Задача №10

Кривошип ОА = 30 см вращается вокруг оси О с угловой скоростью 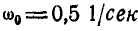. Зубчатое колесо радиуса 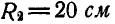катится без скольжения по неподвижному колесу радиуса 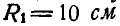и приводит в движение связанный с ним шатун 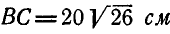. Определить угловую скорость шатуна и скорости точек В и С в момент, когда радиус АВ перпендикулярен к кривошипу ОА (рис. 189).

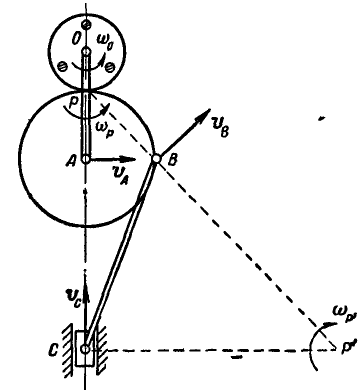
Рис. 189.

Решение. Линейная скорость точки А колеса:

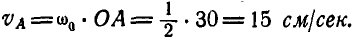
Колесо радиуса 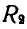совершает плоско-параллельное движение; его мгновенный центр вращения находится в точке Р касания с неподвижным колесом радиуса 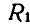. Следовательно, мгновенная угловая скорость 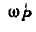подвижного колеса будет:

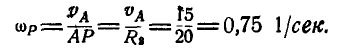
Скорость точки В колеса:

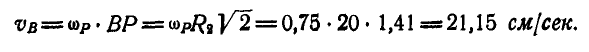
Шатун СВ совершает также плоско-параллельное движение; зная скорость точки В и то, что скорость другой точки С направлена по прямой АС, находим мгновенный центр шатуна Р на пересечении перпендикуляров к скоростям точек В и С.

Мгновенная угловая скорость 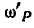шатуна ВС определится:

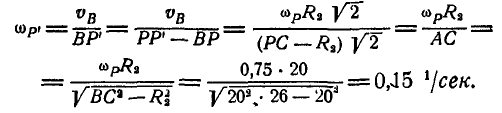
Теперь легко находим скорость точки С шатуна:

• Заказать решение задач по теоретической механике

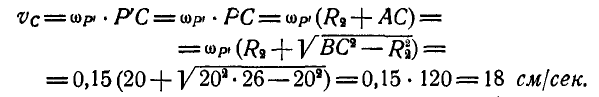
Задача №11

Для данного положения механизма шарнирного четырехзвенника 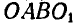(рис. 190, а) найти скорости точек А, В, С и D, если кривошип OA вращается с угловой скоростью 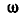и стержень CD соединен жестко с звеном АВ.

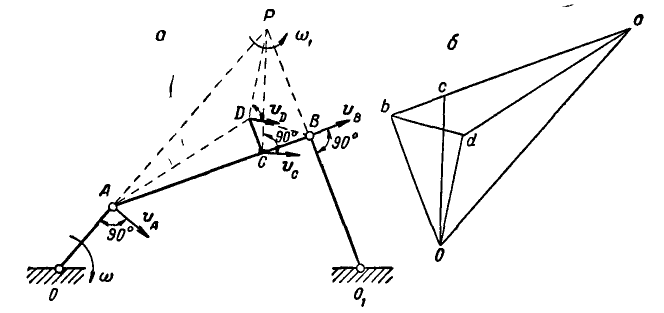
Рис. 190.

Решение. Найдем сначала полюс мгновенного вращения звена АВ; он будет находиться в точке пересечения нормалей OA и 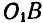к траекториям точек A и В.

Обозначив угловую скорость вращения звена АВ вокруг Р через 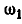находим, что, с одной стороны, 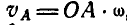, а с другой— 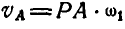, поэтому 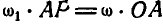, откуда:

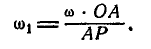
Величины отрезков OA и АР могут быть определены путем непосредственного измерения по чертежу.

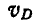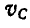Соединяя точки С и D, принадлежащие звену АВ, с полюсом мгновенного вращения Р звена АВ и проведя и перпендикулярно к мгновенным радиусам PD к PC в сторону вращения звена АВ, находим величины скоростей всех точек звена АВ:

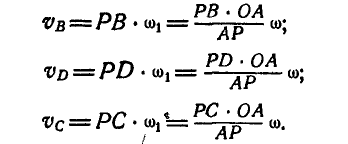
Скорости точек звена АВ можно было бы найти иначе, применив графический способ. Перейдем сейчас к изложению этого способа. Зная положение мгновенного центра Р звена АВ, находим, что 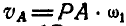и 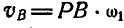, т. е. величины скоростей точек звена АВ пропорциональны расстояниям (или мгновенным радиусам) этих точек от мгновенного центра Р звена.

Возьмем теперь произвольно точку О (рис. 190, б) и отложим по направлениям, параллельным РА и РВ, отрезки Оа и Ob, пропорциональные величинам скоростей 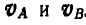. Обозначив коэффициент пропорциональности через а, сможем написать:

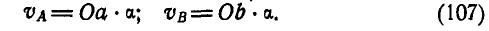
Соединив точки а и b между собой, получим треугольник Oab, подобный' треугольнику РАВ; это следует из того, что стороны этих треугольников пропорциональны.   

Согласно выражениям (107) в треугольнике Oab стороны Оа и Ob изображают в масштабе а скорости точек А и В звена АВ, но повернутые при этом относительно истинных направлений на 90°. Следовательно, стороны Оа и Ob представляют собой векторы повернутых скоросте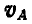й  и .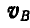

Из треугольника Oab следует: .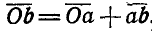

Умножая обе части на масштаб а, получим: 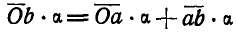, что согласно равенствам (107) может быть представлено в виде: .

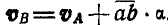Сравнивая это равенство с формулой (106), находим, что .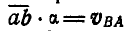

Следовательно, сторона ab треугольника Oab представляет собой в масштабе а повернутую на 90° скорость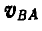 точки В по отношению к точке А.

Треугольник Oab называется планом скоростей отрезка АВ, точка О — полюсом плана скоростей, а — масштабом плана скоростей.

Для построения плана скоростей механизма нет необходимости отыскивать полюсы мгновенных вращений, которые иногда уходят за пределы чертежа. Чтобы построить план скоростей какого-либо звена, например АВ, достаточно знать направления нормалей РА и РВ к траекториям точек А и В.

Для нахождения скорости точки С звена АВ можно было бы на плане скоростей разделить отрезок ab точкой с на части, пропорциональные отрезкам АС и СВ звена, т. е.:

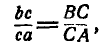
или провести из полюса плана скоростей О отрезок 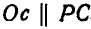. Тогда величина скорости точки С будет .

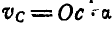Найдем теперь скорость точки D.

Так как точка D принадлежит тому же звену, что и точки А и В, то, как мы видели, направление нормали к траектории точки D будет PD. Проводя из того же полюса плана скоростей О параллель к этой нормали, а из точки а параллель к отрезку AD, получаем в пересечении этих двух прямых точку d, которая определит скорость точки D, а именно: .

Легко видеть, что прямая bd параллельна прямой BD. Из изложенного получаем следующие правила построения плана скоростей.

• 1.    Для построения плана скоростей какого-либо звена, например АВ, надо иметь вектор скорости одной точки звена и направление нормали к траектории (или раму траекторию) другой точки.
• 2.    Должно быть соответствие между планом скоростей и чертежом, т. е. векторы плана скоростей 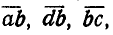изображающие в масштабе а повернутые относительные скорости точек А — по отношению к В; D — по отношению к В; В — по отношению к С, должны быть параллельны соответствующим отрезкам АВ, DB, ВС механизма.
• 3.    Для каждого звена на плане скоростей получается фигура, подобная фигуре звена и одинаково с ней расположенная.

Так, например, на рисунках 190, а и б треугольник abd подобен треугольнику ABD и, кроме того, .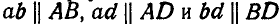

Перейдем теперь к вопросу о центроидах (или полодиях). Пусть отрезок АВ (рис. 191), принадлежащий подвижной плоскости, движется так, что за последующие промежутки времени 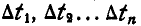он занимает положения 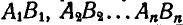при этом траекторией одного из его концов является кривая 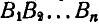, а другого конца — кривая 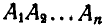. Найдем для каждого из положений отрезка мгновенные центры 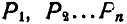и, соединяя их ломаной линией, получим в пределе при 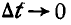кривую, проходящую через точки 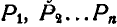. Эта кривая является геометрическим местом полюсов мгновенных вращений отрезка АВ и называется неподвижной центроидой.

Таким образом, неподвижная центроида является геометрическим местом мгновенных центров скоростей на неподвижной плоскости при плоском движении неизменяемой фигуры.

Перенесем теперь все треугольники 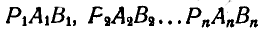в одно из положений, например  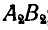тогда эти треугольники займут положения 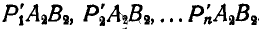. Вершины 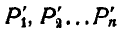перенесенных треугольников образуют геометрическое место, которое называется подвижной центроидой. Если теперь отрезок 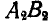будет при своем движении занимать последовательно положения 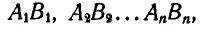то точка 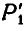совпадает с точкой  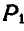, затем  .

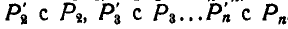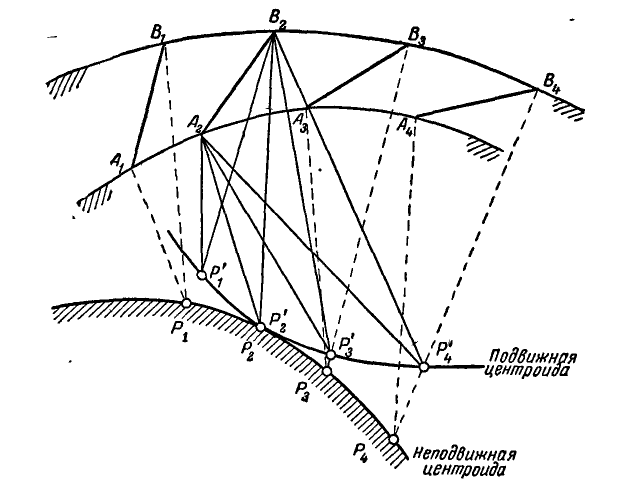
Рис. 191.

Следовательно, подвижная центроида связана с подвижной фигурой и является геометрическим местом мгновенных центров скоростей на движущейся фигуре. Ясно, что в каждый момент времени подвижная и неподвижная центроида имеют общую точку касания.

Следовательно, всякое плоское перемещение подвижной фигуры происходит так, как если бы соединенная с ней подвижная центроида 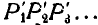 катилась без скольжения по неподвижной центроиде .

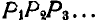Задача №12

Найти неподвижную и подвижную центроиды шатуна АВ (рис. 192), длина которого равна длине кривошипа .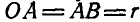

Решение. Полюс мгновенного вращения шатуна АВ находится в точке пересечения прямых ОА и BP, нормалей к траекториям точек А и В. Как видно из чертежа, при всяком положении шатуна 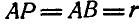, т. е. полюс мгновенного вращения шатуна находится на постоянном расстоянии 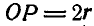от неподвижной точки О и на одном и том же расстоянии 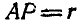от точки А шатуна.

Отсюда заключаем, что неподвижной центроидой является окружность радиуса 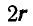с центром в точке О, а подвижной центроидой — окружность радиуса 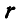с центром в точке А.

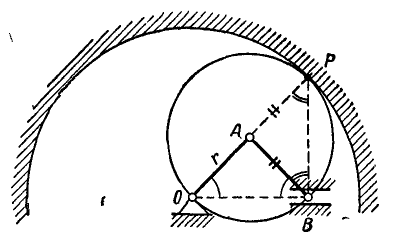
Рис. 192.

Если из прозрачной бумаги вырезать круг радиуса 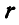, совместить его с подвижной центроидой шатуна (рис. 192), затем вычертить на нем отрезок АВ и начать катить круг так, чтобы подвижная центроида катилась без скольжения по неподвижной, то точка В нашего отрезка будет двигаться по прямой ОВ, а точка А по окружности радиуса ОА. Такой прием получения истинного движения шатуна АВ посредством центроид называется воспроизведением движения и часто применяется при анализе работы механизмов.

Задача №13

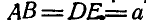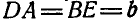Шарнирный четырехзвенник EBAD (рис. 193), в котором и (при этом 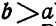), движется так, что вращается DA при неподвижном звене DE. Определить подвижную и неподвижную центроиды звена ВА.

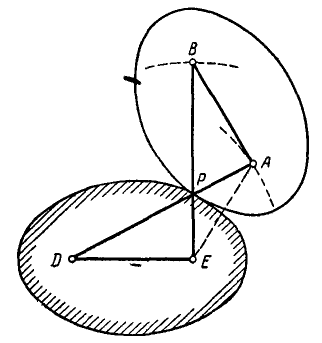
Рис. 193.

Решение. Так как точки А и В движутся по окружностям радиусов и DА и ЕВ, то полюсом мгновенного вращения звена ВА является точка Р пересечения прямых DA и ЕВ.

Из равенства треугольников DAE и ВАЕ заключаем, что . Кроме того, .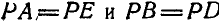

Отсюда следует, что полюс мгновенного вращения Р отстоит от неподвижных точек D и Е, а также от точек А и В звена АВ так, что 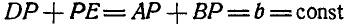, т. е. подвижная и неподвижная центроиды являются одинаковыми эллипсами с большей осью, равной 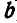, и фокусами в точках D и Е — для неподвижной и в точках В и А— для подвижной центроид. Нетрудно убедиться, что если , то подвижной и неподвижной центроидами звена ВА будут две одинаковые гиперболы с действительными осями, равными 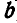, и фокусами в точках Е и D  — для неподвижной и в точках А и В —для подвижной центроид.

Изучив вопрос о скоростях точек подвижной фигуры, обратимся к нахождению ускорений ее точек. Для этого достаточно изучить вопрос об ускорениях точек любого ее отрезка АВ (рис. 194).

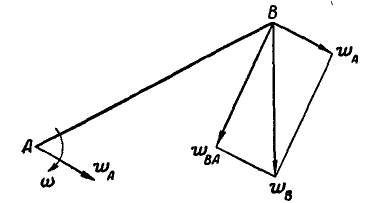
Рис. 194.

Если известно ускорение 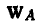какой-либо точки А отрезка, то принимая точку А за полюс и рассматривая на основании доказанной выше теоремы движение отрезка, как поступательное вместе с полюсом и как вращательное вокруг полюса, найдем ускорение точки В по равенству:

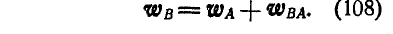
Здесь ускорения 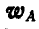 и 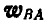от поступательной и вращательной частей движения складываются, так же как и скорости (106), по правилу параллелограмма.

Если известна мгновенная угловая скорость 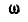и мгновенное угловое ускорение 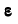отрезка АВ, то ускорение точки В по отношению к точке А может быть разложено на составляющие по направлению ВА и к нему перпендикулярное:

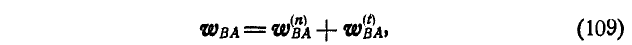
где

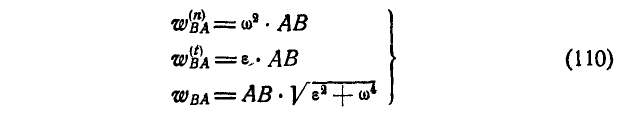
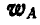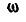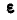Покажем теперь, что в каждый момент существует точка движущейся фигуры, ускорение которой равно нулю. Пусть движение фигуры задано отрезком АВ (рис. 195) и пусть ускорение точки А, а и —мгновенные угловая скорость и угловое ускорение отрезка. Если принять точку А за полюс, то ускорения любых точек отрезка С, В...  могут быть найдены по формуле (108):

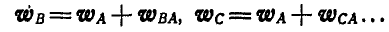
Отсюда следует простой способ построения векторов ускорений точек отрезка, если известно ускорение какой-либо одной его точки, например А, и мгновенные угловая скорость 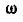и угловое ускорение 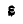отрезка. 

Принимая сначала точку А (полюс) за неподвижную, найдем, что ускорения 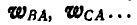всех точек  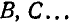отрезка пропорциональны расстояниям этих точек от полюса и параллельны между собой; тогда концы векторов, изображающих эти ускорения, лягут на прямую AM. Если мы дадим теперь всему отрезку поступательное перемещение с ускорением 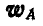полюса, то к ускорениям 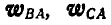прибавится ускорение полюса и концы векторов полных ускорений 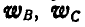точек 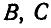лягут на прямую 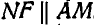. Изложенный метод определения ускорений применим к любому отрезку плоской фигуры.

Отложив, например, от точки А отрезок АЕ, составляющий угол 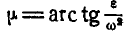с направлением вектора 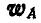, и построив для точки Е этого отрезка вектор 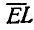, изображающий ускорение точки Е по отношению к полюсу А, найдем, что полное ускорение 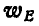точки Е изобразится вектором 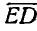. Ускорение точки Е легко получить, если соединить точку А с С и провести из точки N отрезок ND || AL.

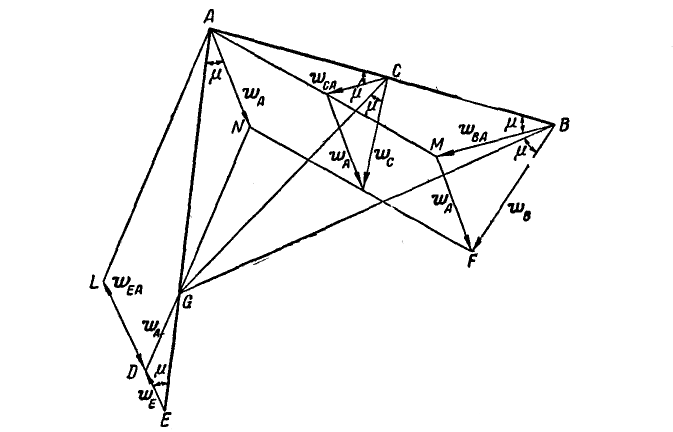
Рис. 195.

Таким образом, прямая ND аналогична прямой NF является геометрическим местом концов векторов, изображающих полные ускорения точек отрезка АЕ. Нетрудно видеть, что ускорение точки О отрезка АЕ равно нулю; эта точка называется мгновенным центром ускорений.

Если принять мгновенный центр ускорения G за полюс, то, вычисляя ускорения точек В, С отрезка АВ по формуле (108), найдем:

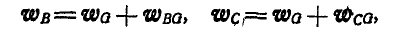
но так как 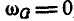, то 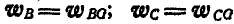, и, кроме того, по формуле (92), получаем:

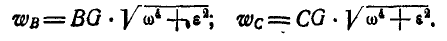
Следовательно, ускорения точек фигуры пропорциональны расстояниям их от мгновенного центра ускорений и образуют с отрезками, соединяющими эти точки с мгновенным центром ускорений, один и тот же угол 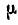, определяемый равенством (93).

Подобно тому, как скорости, точек плоской, фигуры пропорциональны расстояниям их до мгновенного центра скоростей и образуют с мгновенными радиусами углы 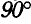, так и ускорения точек плоской фигуры пропорциональны расстояниям их до мгновенного центра ускорений и образуют с этими направлениями один и тот же угол 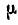, определяемый равенством:

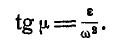
Не следует, однако, думать, что мгновенный центр скоростей Р и мгновенный центр ускорений G совпадают между собой. Это имеет место только для случая вращения тела вокруг неподвижной оси.

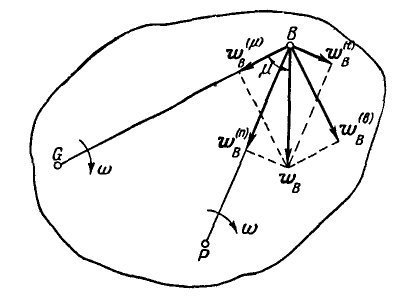
Рис. 196.

Если за полюс принята точка G, то полное ускорение какой-либо точки В плоской фигуры (рис. 196) может быть представлено в виде двух составляющих: 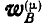— центростремительного и 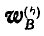— вращательного ускорений; при этом:

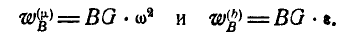
Если же за полюс принята точка Р, то полное ускорение точки В удобно разложить на нормальное 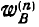 и касательно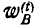е  где:

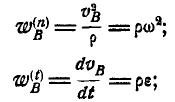
при этом радиус кривизны траектории 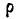направлен по BP, но не равен BP.

Задача №14

Найти ускорение любой точки обода колеса, катящегося без скольжения по прямолинейному рельсу с постоянной скоростью 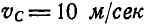, если радиус колеса 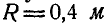(рис. 197).

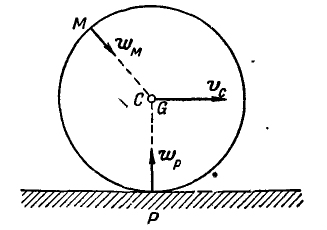
Рис. 197. 

Решение. Мгновенный центр ускорений О находится в центре колеса С, так как эта точка движется прямолинейно и равномерно. Мгновенный же центр скоростей находится в точке Р касания колеса с рельсом, поэтому угловая скорость и угловое ускорение колеса соответственно равны:

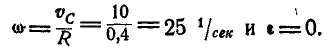
Отсюда заключаем, что ускорение любой точки обода направлено к центру колеса и равно по величине:

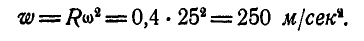
Задача №15

Колесо катится без скольжения в вертикальной плоскости по наклонному прямолинейному пути. Найти ускорения концов двух взаимно-перпендикулярных диаметров колеса, из которых один параллелен рельсу, если в рассматриваемый момент времени скорость центра колеса 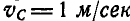, ускорение центра колеса 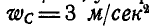, радиус колеса  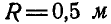(рис. 198).    V

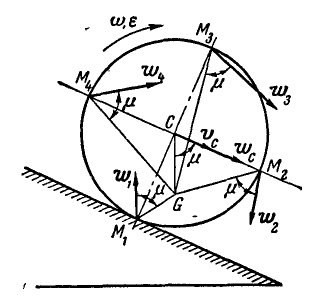
Рис. 198.

Решение. Центр мгновенного вращения колеса находится в точке касания, поэтому его угловая скорость:  

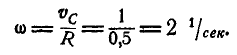
Центр колеса движется прямолинейно, следовательно его ускорение:

Отсюда находим, что в данный момент времени угловое ускорение колеса:    

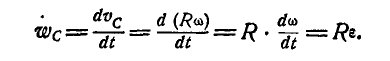
Зная ускорение какой-либо точки плоской фигуры, в нашем случае ускорение 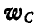точки С, а также для данного момента величину и направление угловой скорости  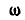и углового ускорения 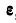, найдем положение мгновенного центра ускорений G. Он должен лежать на полупрямой, выходящей из точки С, ускорение которой нам известно, и образующей с вектором этого ускорения угол 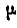, определяемый равенством (93):

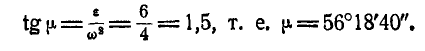
При этом угол 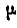отсчитывается от вектора ускорения 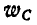в направлении .

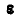Положение мгновенного центра ускорений на полупрямой определится посредством равенства (92):

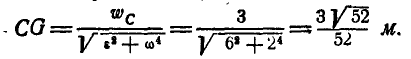
Найдя мгновенный центр ускорений, можно построить вектор ускорения любой точки колеса, например 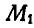соединив точку G с точкой 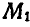и отложив ускорение 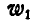от прямой 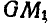на угол 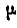в сторону, противоположную направлению. Величина же ускорения точки 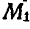найдется по формуле:

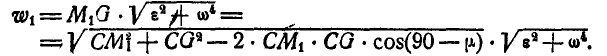
Так как

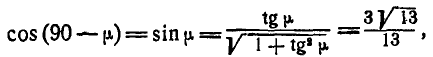
то окончательно находим: 

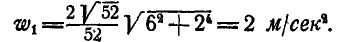
Аналогично находим ускорения остальных точек колеса:

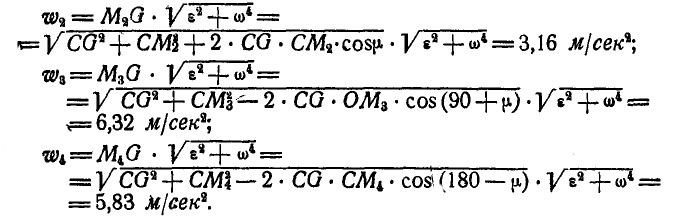
Векторы ускорений для рассматриваемых точек колеса построены на чертеже.

Задача №16

Найти ускорения пальца кривошипа А, ползуна В и точки С середины шатуна АВ кривошипно-шатунного механизма, если длины шатуна и кривошипа одинаковы: 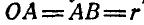и кривошип OA вращается с постоянной угловой скоростью 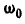(рис. 199).

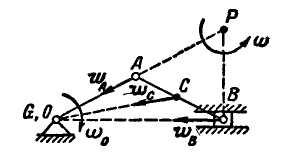
Рис. 199.

Решение. Ускорение точки А равно 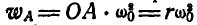и направлено от А к О.

Полюс мгновенного вращения шатуна АВ найдется в пересечении прямых OA и 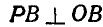. Так как 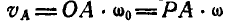» и 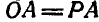, то угловая скорость шатуна и будет постоянна. Поэтому угловое ускорение шатуна .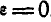

Мгновенный центр ускорений 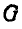шатуна АВ будет находиться на полупрямой, выходящей из точки А, ускорение 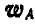которой нам известно, и образующей с вектором этого ускорения угол 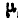, определяемый равенством:

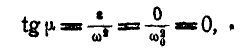
откуда .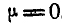

Положение точки G на полупрямой АО определится равенством (92):

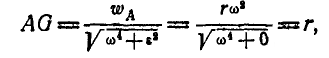
т. е. мгновенный центр ускорений G совпадает с осью вращения О кривошипа. Отсюда ускорения точек В и С определятся:

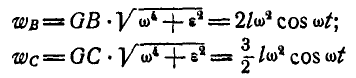
и будут направлены к точке О.

Задача №17

Кривошип ОА механизма режущего аппарата сенокосилки вращается с постоянной угловой скоростью 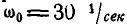и с помощью шатуна АВ приводит в движение нож, соединенный с ползуном В, движущимся вдоль горизонтальных направляющих (рис. 200).

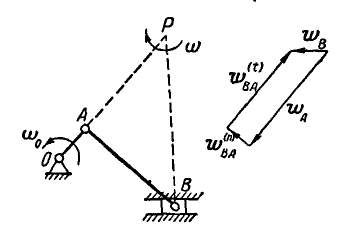
Рис. 200.

Найти угловую скорость 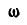и угловое ускорение 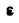шатуна, а также ускорение 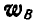ползуна В в положении, когда кривошип и шатун взаимно перпендикулярны и образуют с горизонтальной прямой углы 45°. Длины: АО = 5 см, АВ = 50 см.

Решение. Найдем мгновенный центр Р шатуна АВ; тогда скорость точки А будет:

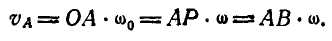
Отсюда угловая скорость шатуна:

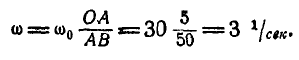
Ускорение точки В может быть найдено из равенств (108) и (109):

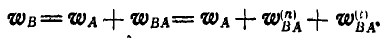
Это уравнение можно переписать иначе:

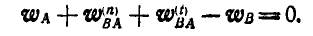
Знак минус у вектора 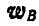указывает на то, что в многоугольнике векторов, построенном на основании полученного векторного уравнения, направление стрелки вектора. 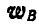противоположно течению стрелок остальных векторов. Определим ускорения:  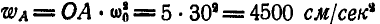и направлено от А к О; 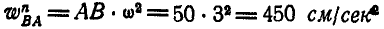и направлено от В к А.

Зная, что вектор 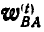перпендикулярен к АВ, а вектор 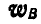направлен горизонтально, строим многоугольник векторов (рис. 200), из которого находим:

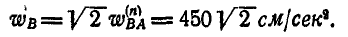
Угловое ускорение шатуна:

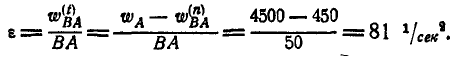
Задача №18

Равносторонний треугольник ABC со стороной а = 6 см движется в плоскости чертежа. Ускорения вершин А и В в данный момент времени равны 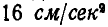и направлены по сторонам треугольника (рис. 201). Определить ускорение третьей вершины С треугольника.

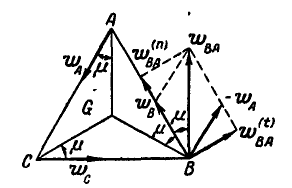
Рис. 201.

Решение. Применяя равенство (108), имеем: 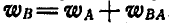, откуда находим, что .

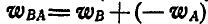Из последнего равенства следует, что для нахождения вектора 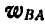следует в точке В построить вектор 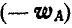, противоположный заданному вектору 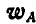, а затем векторы 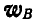и 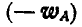сложить геометрически. Проектируя вектор 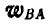на направления АВ и перпендикулярное к нему, находим:

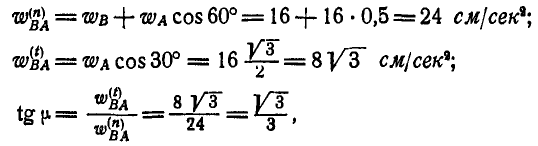
откуда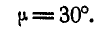 

Откладывая от векторов 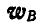и 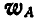в направлении против часовой стрелки полупрямые под углом 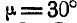, получим в пересечении их мгновенный центр ускорений G. Соединив G с точкой С и отложив от GC в направлении по часовой стрелке угол 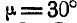, получим направление вектора 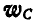ускорения точки С.

Определим угловую скорость и угловое ускорение треугольника.

Согласно равенствам (110) имеем:

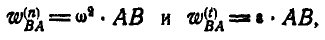
откуда:

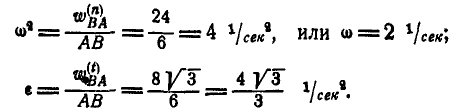
Ускорение:    

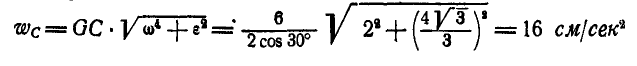
и направлено по CВ от С к В.