
Площади фигур в геометрии - формулы с примерами
Содержание:
Аксиома равенства площадей: Площади конгруэнтных фигур равны.
Аксиома сложения площадей: Площадь фигуры, разделённой на части не имеющих общих внутренних точек, равна сумме площадей этих фигур.
Высота параллелограмма
Определение. Перпендикуляр, опушенный из любой точки одной стороны параллелограмма на прямую, содержащую противоположную сторону, называется высотой параллелограмма. Если параллелограмм не ромб, то он имеет две высоты разной длины (на рисунке это BE и BF).
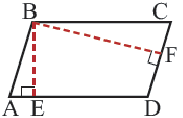
Практическая работа: Начертите на листе бумаги параллелограмм и его высоту. Разрежьте параллелограмм по высоте, как показано на рисунке, и приклейте к правой стороне. Выскажите своё мнение о полученной фигуре. Запишите формулу нахождения площади прямоугольника. Обобщите мнение о том, что такое площадь параллелограмма.

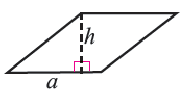
Так как длина стороны параллелограмма равна длине прямоугольника, а высота параллелограмма равна ширине прямоугольника, то площадь параллелограмма равна площади прямоугольника.
Площадь параллелограмма
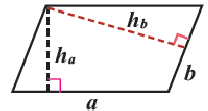
Площадь параллелограмма равна произведения стороны и высоты, проведённой к данной стороне: 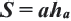 или
или 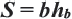
Площадь треугольника
Площадь треугольника равна половине произведения стороны и высоты, проведённой к данной стороне, 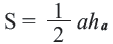
Обозначим высоты, проведённые к сторонам 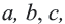 соответственно как
соответственно как 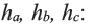
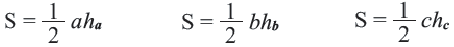
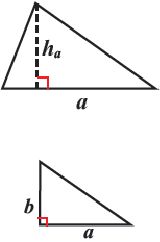
Площадь прямоугольного треугольника равна половине произведения катетов. 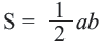
Формула Герона для нахождения площади треугольника
Для треугольника со сторонами 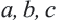 верна формула нахождения площади
верна формула нахождения площади 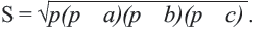 Эта формула называется формулой Герона. Здесь
Эта формула называется формулой Герона. Здесь 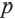 полупериметр треугольника:
полупериметр треугольника: 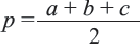
Задача. Найдём площадь треугольника со сторонами 13 см, 14 см и 15 см. Дано: 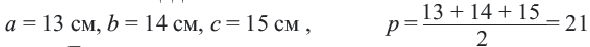
По формуле Герона 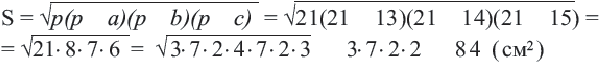
Площадь трапеции
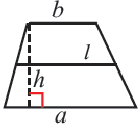
Высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
Площадь трапеции равна произведению половине суммы оснований и высоты: 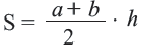
Площадь трапеции равна произведению средней линии и высоты: 
Площадь ромба
1. Площадь ромба равна произведению стороны и высоты: 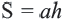
Отметим что высоты ромбы равны.
2. Площадь ромба равна половине произведения диагоналей: 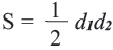
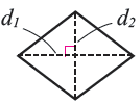
3. Площадь любого произвольного выпуклого четырёхугольника, диагонали которого взаимно перпендикулярными равна t половине произведения диагоналей: 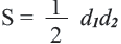
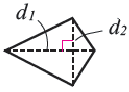
Площадь поверхности вращения
Определение 1. Пусть L – простая кривая на плоскости заданная явно в виде 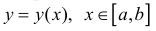 (см. § 30). Пусть функция y=y(x) - непрерывна и неотрицательна
(см. § 30). Пусть функция y=y(x) - непрерывна и неотрицательна 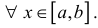 Разобьем отрезок [a b] на n частичных отрезков точками
Разобьем отрезок [a b] на n частичных отрезков точками 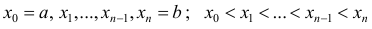 и обозначим это разбиение
и обозначим это разбиение 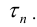 Пусть
Пусть
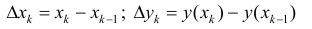
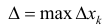 - диаметр разбиения.
- диаметр разбиения.
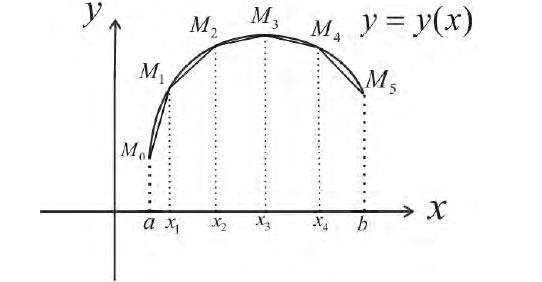
Пусть 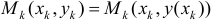 точки на кривой
точки на кривой 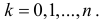 Рассмотрим ломаную последовательно проходящую через точки
Рассмотрим ломаную последовательно проходящую через точки 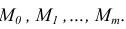 При вращении кривой
При вращении кривой 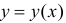 вокруг оси Ох каждое звено
вокруг оси Ох каждое звено 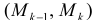 ломаной описывает поверхность
ломаной описывает поверхность
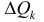 площадь которой
площадь которой 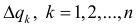 (боковая поверхность усеченного конуса).
(боковая поверхность усеченного конуса).
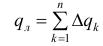 - площадь всей поверхности.
- площадь всей поверхности.
Если ∃ предел при Δ → 0 площади 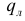 не зависящий от способа разбиения отрезка, то он называется площадью q поверхности вращения кривой L вокруг оси Ox .
не зависящий от способа разбиения отрезка, то он называется площадью q поверхности вращения кривой L вокруг оси Ox .
Таким образом 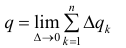 (1)
(1)
Замечание. Пусть функция y=f(x) – непрерывно-дифференцируема на отрезке [a b] , тогда 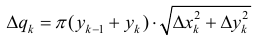 – площадь боковой поверхности усеченного конуса;
– площадь боковой поверхности усеченного конуса; 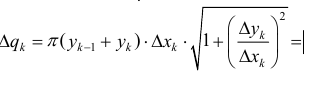 (по теореме Лагранжа (см. теорему 4 § 12)
(по теореме Лагранжа (см. теорему 4 § 12)
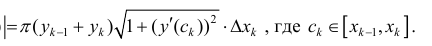
Поэтому
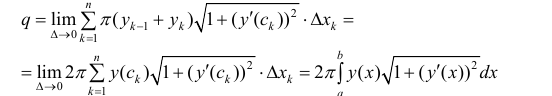
Таким образом:
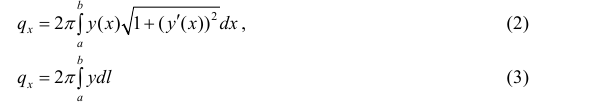
Где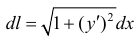 – дифференциал дуги. Формулы (2) и (3) приведены для кривых L, лежащих выше оси Ох. В общем случае верны формулы:
– дифференциал дуги. Формулы (2) и (3) приведены для кривых L, лежащих выше оси Ох. В общем случае верны формулы:
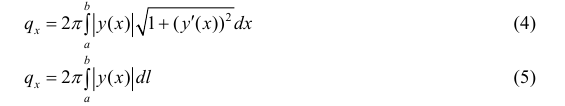
Если кривая L задана параметрически в виде
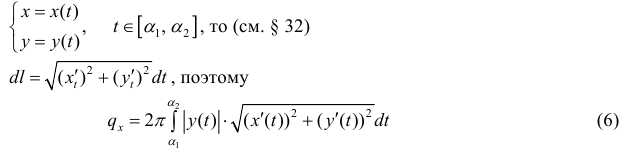
Для кривой L заданной в полярных координатах уравнением 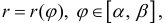
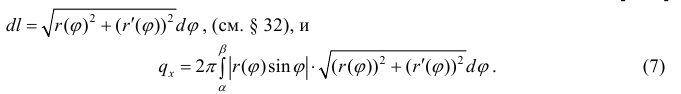
Пример №1
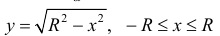 – верхняя полуокружность радиуса R.
– верхняя полуокружность радиуса R.
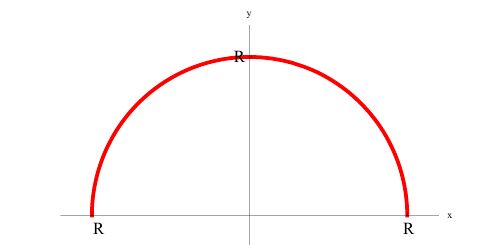
Найдем площадь поверхности при вращении вокруг оси Ох.
Решение.
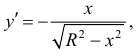 , по формуле (2):
, по формуле (2): 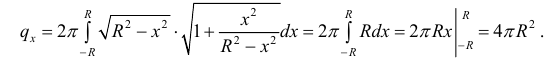
Пример №2
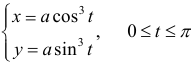 – верхняя половина астроиды
– верхняя половина астроиды
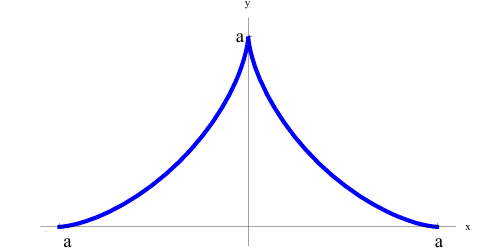
Найдем 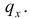
Решение.
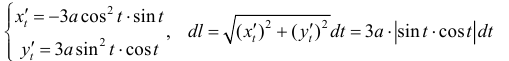 (см. пример 1 § 32). Пусть
(см. пример 1 § 32). Пусть 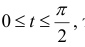 тогда по формуле (6):
тогда по формуле (6):
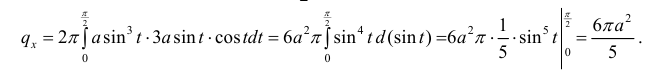
Поэтому площадь всей поверхности 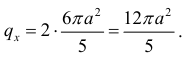
Пример №3
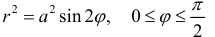 – лепесток лемнискаты, расположенный в первой четверти
– лепесток лемнискаты, расположенный в первой четверти
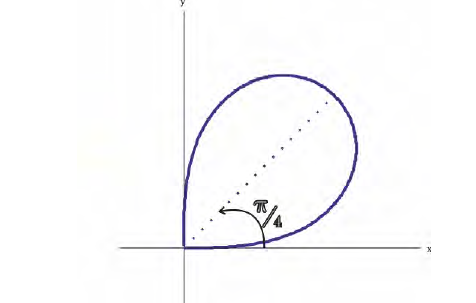
Найдем 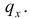
Решение.
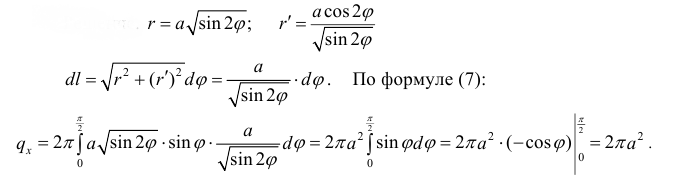
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |