Площадь треугольника - определение и вычисление с примерами решения

Площадь треугольника:

Теорема (о площади треугольника). Площадь треугольника равна половине произведения его стороны на высоту, к ней проведенную.

Доказательство:

Пусть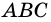

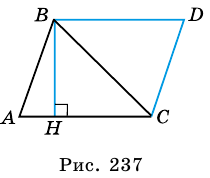
Докажем, что

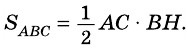
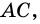1) Проведем через вершину прямую, параллельную  а через вершину 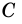- прямую, параллельную  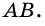Получим параллелограмм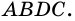

2) 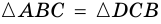 (по трем сторонам). Поэтому

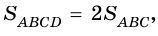откуда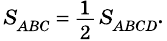 

3) Так как 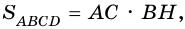 то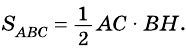

В общем виде формулу площади 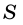треугольника можно записать так:

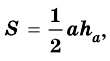
где 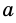- сторона треугольника, 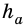- высота, проведенная к ней.

Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов.

Следствие 2. Если сторона одного треугольника равна стороне другого треугольника, то площади таких треугольников относятся как их высоты, проведенные к этим сторонам.

Следствие 3. Если высота одного треугольника равна высоте другого треугольника, то площади этих треугольников относятся как стороны, к которым проведены эти высоты.

Пример:

Докажите, что если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, образующих этот угол.

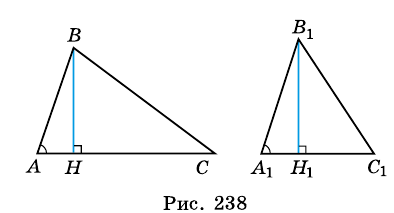
Доказательство:

Рассмотрим 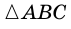и 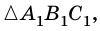у которых 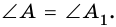Проведем высоты 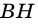и 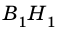(рис. 238).

1) Имеем:

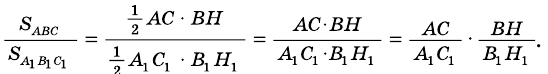
2) 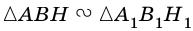(по острому углу), поэтому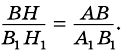 

3) Имеем: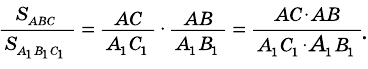 

Пример:

Найдите площадь равностороннего треугольника, сторона которого равна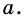

Решение:

Пусть 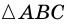- равносторонний со стороной  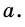Тогда 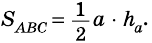 В равностороннем треугольник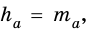е  где 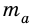- медиана. Но  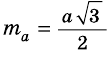(§ 18, задача 4), поэтому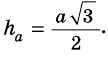 

Следовательно,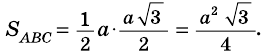 

Ответ.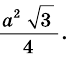

Пример:

Стороны треугольника равны 8 см, 15 см и ^ 17 см. Найдите высоту треугольника, проведенную к его наибольшей стороне.

Решение:

Так как 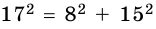(т. е. 289 = 289), то по теореме, обратной теореме Пифагора, треугольник является прямоугольным. Прямой угол является противолежащим к стороне, равной 17 см.

Пусть на рис. 239 изображен прямоугольный треугольник, у которого 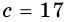см -гипотенуза, 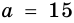и 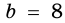см - катеты, 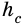- высота. Найдем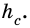

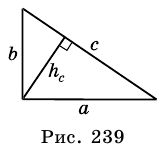
Площадь этого треугольника можно найти

по формулам: 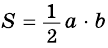или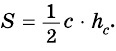

Тогда 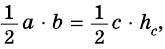то есть  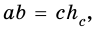откуда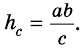

Таким образом, имее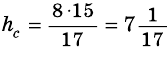м: (см).

Ответ. 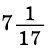см.

Теорема (формула площади треугольника)

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

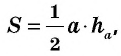
где 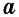 — сторона треугольника,  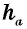— проведенная к ней высота.

Доказательство:

 Пусть 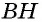 — высота треугольника 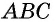(рис. 148). Докажем, что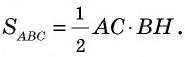 

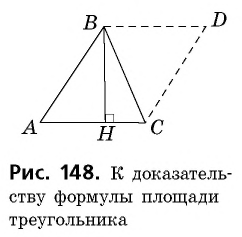
Проведем через вершины 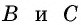 прямые, параллельные сторонам треугольника, и обозначим точку их пересечения  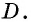Таким образом, мы «достроили» треугольник  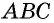до параллелограмма  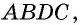в котором отрезок  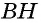также является высотой, проведенной к стороне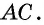 

По формуле площади параллелограмма 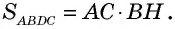 Треугольники  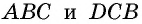равны по трем сторонам (у них сторона  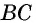общая,  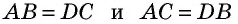как противолежащие стороны параллелограмма). Эти треугольники имеют равные площади. Тогда площадь треугольника  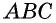составляет половину площади параллелограмма  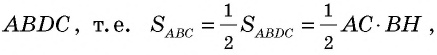что и требовалось доказать. 

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов:

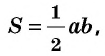
где 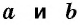 — катеты прямоугольного треугольника.

Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.

Следствие 2

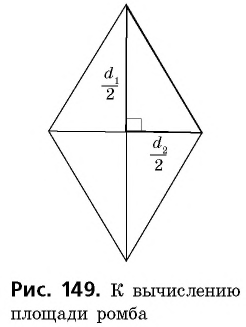
Площадь ромба равна половине произведения его диагоналей:

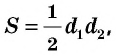
где 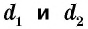 — диагонали ромба.

Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами 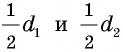 (рис. 149). Используя следствие 1, имеем:

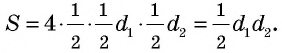
Следствие 3

Площадь равностороннего треугольника со стороной 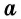 вычисляется по формуле

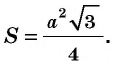
Обоснуйте это следствие самостоятельно.

Опорная задача

Медиана делит треугольник на два равновеликих треугольника. Докажите.

Решение:

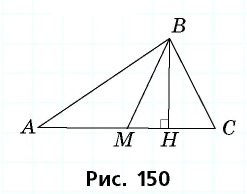
Пусть 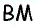 — медиана треугольника  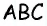(рис. 150).

Проведем высоту 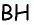 треугольника  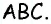Этот отрезок является одновременно высотой треугольника  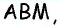проведенной к стороне  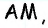и высотой треугольника  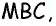проведенной к стороне  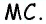Учитывая равенство отрезков  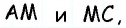имеем:

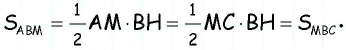
Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.

Докажите эти утверждения самостоятельно.