Площадь параллелограмма - определение и вычисление с примерами решения

Теорема (о площади параллелограмма). Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

Доказательство:

Пусть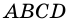

1) Проведем высоту 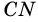к прямой, содержащей сторону 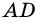параллелограмма.

2) 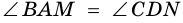(как соответственные углы при параллельных прямых 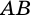и и 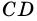секущей  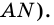Поэтому  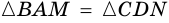(по гипотенузе и острому углу). 

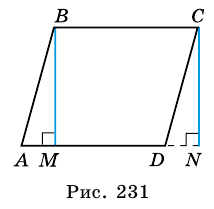
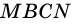3) Параллелограмм состоит из трапеции и треугольника  а прямоугольник - из трапеции 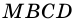и треугольника  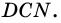Так как треугольник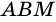и и 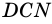равны, то равны и их площади, а потому равными будут площади параллелограмма 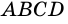и прямоугольника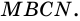

4) 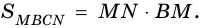 Но 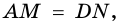 и поэтому  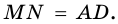Следовательно,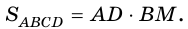

Заметим, что если основание высоты 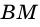 - точка 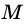-совпадает с точкой 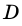или лежит на продолжении стороны 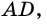то доказательство теоремы будет аналогичным.

В общем виде формулу площади 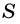параллелограмма можно записать так:

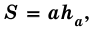
где 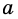- сторона параллелограмма, 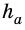- высота, к ней проведенная.

Пример:

Докажите, что высоты ромба, проведенные из одной вершины, равны.

Доказательство:

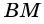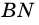Пусть - данный ромб, и  - его высоты (рис. 232).

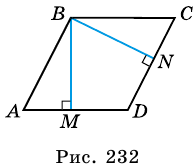
Ромб является параллелограммом, поэтому 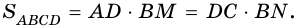Но 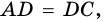а значит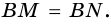

Пример:

Периметр параллелограмма равен 36 см, а его высоты - 4 см и 5 см. Найдите площадь параллелограмма.

Решение:

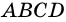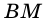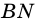1) Пусть - данный параллелограмм, и - его высоты (рис. 232),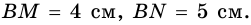

2) 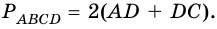 По условию  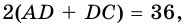поэтому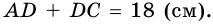

3) Пусть 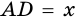см, тогда 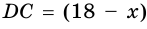см.

4) Так как по формуле площади параллелограмма 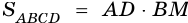или 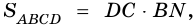имеем уравнение:  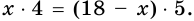То есть 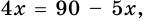откуда 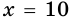(см).

5) Тогда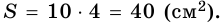

Ответ. 40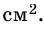

Площадь параллелограмма

С помощью формулы площади прямоугольника можно доказать формулу площади произвольного параллелограмма.

Теорема (формула площади параллелограмма)

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне:

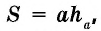
где 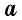 — сторона параллелограмма,  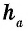— проведенная к ней высота.

Доказательство:

 Пусть 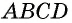 — данный параллелограмм, не являющийся прямоугольником (рис. 145, а). Проведем его высоты  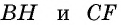и докажем, что  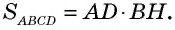Четырехугольник  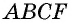является прямоугольной трапецией, площадь которой можно вычислить двумя способами — как сумму площадей параллелограмма  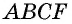и треугольника  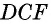или как сумму площадей прямоугольника  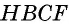и треугольника  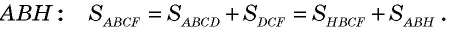Треугольники  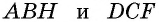равны по гипотенузе и катету  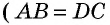как противолежащие стороны параллелограмма,  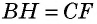 как расстояния между параллельными прямыми). Следовательно, эти треугольники имеют равные площади. Тогда площади параллелограмма  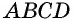и прямоугольника  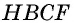также равны, т.е.  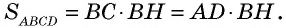Случаи, когда точка  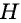не является внутренней точкой отрезка  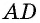(рис. 145, б, в), рассмотрите самостоятельно. 

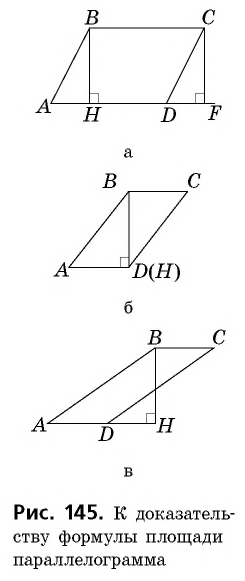
Пример:

Площадь параллелограмма равна  а длины его высот — 3 см и 4 см. Найдите периметр параллелограмма.

Решение:

Пусть дан параллелограмм с площадью 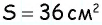 и высотами  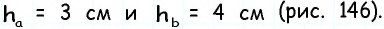(рис. 146).

Поскольку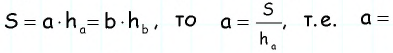  

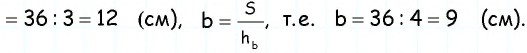
Следовательно, периметр параллелограмма равен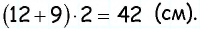 

Ответ: 42 см.

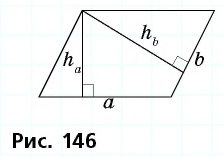
Решая приведенную задачу, можно заметить интересную закономерность: чем больше сторона параллелограмма, тем меньше проведенная к ней высота.