Первый закон термодинамики - формулы и определение с примерами

Содержание:

Первый закон термодинамики:

При изучении физики в 9 классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия? Если бутылку, заполненную до половины водой при комнатной температуре, встряхивать в течение нескольких минут, то окажется, что вода нагрелась на 1—2 °С. Каким образом нагрелась вода?

В середине XIX века известный английский физик Дж. Джоуль (1818— 1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814—1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX века Г. Гельмгольца (1821 —1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы. Согласно этому закону при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.

Для термодинамических систем (в термодинамике обычно рассматривают макроскопически неподвижные системы) закон сохранения и превращения энергии называют первым законом термодинамики. Согласно первому закону термодинамики, приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами:

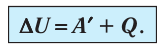
Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком (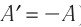

Если система представляет собой действующее устройство, периодически возвращающееся в исходное состояние, то при этом AU-0 и A-Q. Механизм, который мог бы совершать работу без изменения состояния составляющих его тел и без теплопередачи от внешних тел, называют «вечным двигателем первого рода». Поэтому первый закон термодинамики можно сформулировать и следующим образом: невозможен вечный двигатель первого рода, т. е. такой двигатель, который при неизменном значении собственной внутренней энергии совершал бы работу большую, чем энергия, получаемая им извне.

Применим первый закон термодинамики к различным изопроцессам, происходящим с идеальным одноатомным газом.

Изохорный процесс

Пусть идеальный одноатомный газ находится в цилиндрическом сосуде, закрытом неподвижным поршнем (V = const). Нагреем сосуд с газом. Объём газа остаётся практически постоянным (тепловым расширением сосуда пренебрегаем) (рис. 60), следовательно, работа силы давления газа А= 0. Тогда первый закон термодинамики примет вид
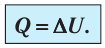(11.З)

Это означает, что всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии. При этом приращение внутренней энергии газа 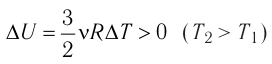(рис. 61, а). А если газ при изохорном

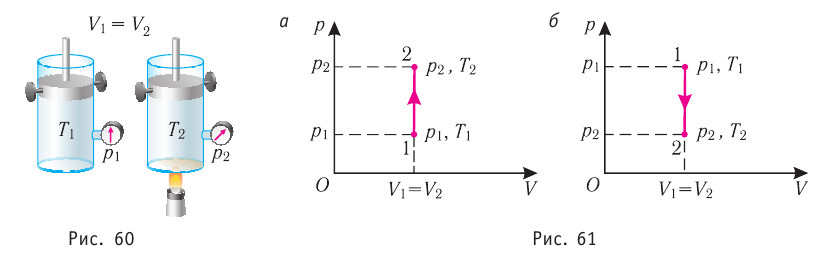
процессе отдаёт количество теплоты, то его внутренняя энергия убывает:

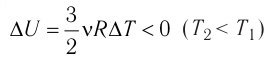(рис. 61, б).

Изотермический процесс

Пусть цилиндрический сосуд с газом под поршнем находится в термостате — устройстве, в котором поддерживается постоянная температура. В этом случае внутренняя энергия идеального одноатомного газа 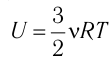остаётся постоянной, а её изменение 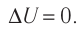Тогда первый закон термодинамики примет вид
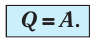(11.4)

Какие выводы следуют из этого? Если с помощью внешнего устройства медленно перемещать поршень в сосуде так, чтобы объём газа увеличивался (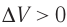, поскольку 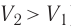) (рис. 62), то работа силы давления расширяющегося газа А > 0 (рис. 63, а). При одинаковой первоначальной температуре термостата и газа теплопередачи не происходит. Положительная работа силы давления расширяющегося газа совершается за счёт уменьшения его внутренней энергии, а значит, и температуры. Тут же возникает теплопередача от термостата газу. При медленном перемещении поршня в сосуде температура газа успевает выравняться, а реально происходящий процесс близок к изотермическому процессу, при котором расширяющийся газ получает некоторое количество теплоты (Q > 0) от термостата.

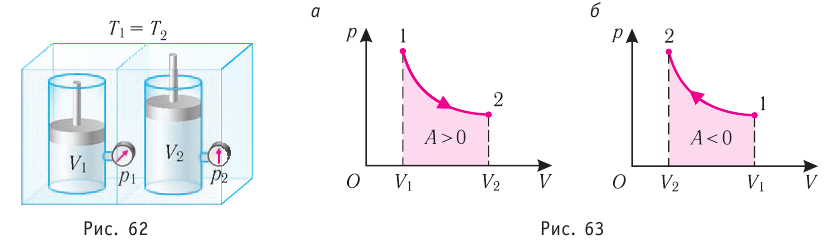
Если же внешнее устройство обеспечивает медленное уменьшение объёма газа в сосуде (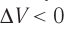, так как 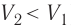), то работа силы давления при сжатии газа А < 0 (рис. 63, б) приводит к увеличению внутренней энергии и, следовательно, его температуры. В результате возникает теплопередача от газа термостату. При сжатии газ отдаёт термостату некоторое количество теплоты Q < 0. Изотермическое сжатие газа происходит за счёт работы внешних сил: А' > 0.

Изобарный процесс

Пусть газ находится в цилиндрическом сосуде, закрытом поршнем, который может свободно или под постоянной нагрузкой перемещаться (рис. 64). Нагреем газ, передав ему некоторое количество теплоты (Q > 0). Согласно первому закону термодинамики (11.2) переданное газу количество теплоты частично расходуется на увеличение внутренней энергии 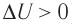) системы и частично идёт на совершение работы силой давления газа при его расширении (A>0)(рис. 65, a):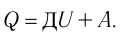

При изобарном процессе работа расширения (сжатия) газа 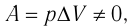, и первый закон термодинамики принимает вид

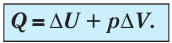(11.5)

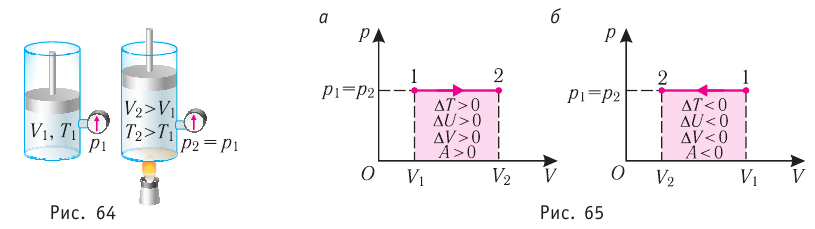
При изобарном сжатии газа внешние силы совершают работу А' > 0. Чтобы давление газа при этом оставалось постоянным, газ необходимо охлаждать, т. е. он должен отдавать в окружающую среду некоторое количество теплоты (Q < 0). Понижение температуры газа при изобарном сжатии приводит к уменьшению его внутренней энергии (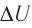<0). Работа силы давления газа при сжатии А < 0 (рис. 65, б).

Удельная теплоёмкость вещества зависит не только от его свойств, но и от характера осуществления процесса теплопередачи. Действительно, из формулы (10.4) следует, что удельная теплоемкость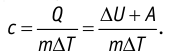

Тогда согласно первому закону термодинамики при изохорном процессе (11.3)

удельная теплоёмкость идеального газа 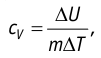а при изобарном (11.5) —

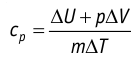Таким образом, для одинакового увеличения температуры при изобарном нагревании единице массы газа необходимо передать большее количество теплоты, чем при изохорном нагревании, т. е.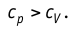

Это объясняется тем, что при постоянном давлении часть подводимой энергии расходуется на совершение силой давления газа работы при расширении.

Расширение жидких и твёрдых тел при нагревании при постоянном давлении значительно меньше, чем газов, поэтому для них 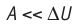и их удельные теплоёмкости слабо зависят от характера процесса.

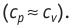Адиабатный процесс

Адиабатным называют процесс, в ходе которого термодинамическая система не получает и не отдаёт энергию путём теплопередачи. Таким образом, при адиабатном процессе

Q = 0.
Применяя к этому процессу первый закон термодинамики, получим:
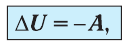(11.6)
или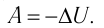

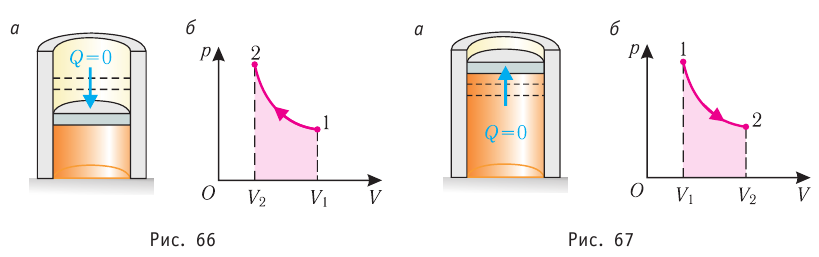
При адиабатном процессе изменение внутренней энергии системы происходит только за счёт совершения работы. Если внешние силы совершают работу по сжатию газа (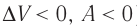) (рис. 66, а, б), то внутренняя энергия газа увеличивается (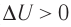), газ нагревается. Если сила давления газа совершает работу по расширению (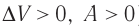) (рис. 67, а, б), то внутренняя энергия газа уменьшается (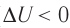), газ охлаждается не допускает теплопередачи), а за счёт скорости протекания процесса.

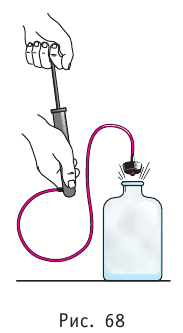
Если процесс протекает очень быстро, то теплопередача практически не сказывается. Очень нагляден опыт, иллюстрирующий уменьшение температуры газа при его адиабатном расширении. Используя насос, через отверстие в пробке будем накачивать в стеклянный сосуд воздух (рис. 68). Через некоторый промежуток времени накачивания сжатый воздух совершит работу по преодолению силы трения, с которой сосуд действует на пробку, и силы атмосферного давления. Теплопередача между сосудом и окружающими телами не успевает проявиться за тот малый промежуток времени, пока пробка вылетает из сосуда. Уменьшение внутренней энергии воздуха в сосуде выражается в понижении его температуры, что приводит к конденсации водяных паров, т. е. к образованию тумана.

В качестве примера адиабатного процесса можно привести охлаждение воздуха в атмосфере. Нагретый возле поверхности Земли воздух при быстром подъёме в верхние слои атмосферы расширяется почти адиабатно и при этом резко охлаждается. Водяной пар в нём конденсируется в маленькие капли воды и кристаллики льда, образуя облака. Близкий к адиабатному процесс используют в двигателях внутреннего сгорания.

Обратимый адиабатный процесс относят к изопроцессам, так как он характеризуется постоянством функции состояния, называемой энтропией. В отличие от остальных изопроцессов при обратимом адиабатном процессе происходят изменения давления, объёма и температуры. График адиабатного процесса в координатах (р, V) похож на график изотермического процесса (рис. 69). Однако одному и тому же изменению объёма 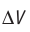при адиабатном процессе соответствует большее изменение давления, чем при изотермическом: 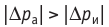(рис. 69).

Это объясняется тем, что в случае адиабатного расширения давление 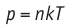уменьшается не только за счёт увеличения объёма газа (и уменьшения концентрации частиц), но и за счёт уменьшения температуры. При изотермическом расширении давление газа уменьшается только за счёт уменьшения концентрации частиц.

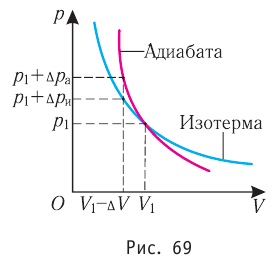
1. Приращение внутренней энергии термодинамической системы при

переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами:

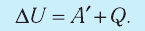
2.    Количество теплоты, полученное или отданное термодинамической системой при взаимодействии с внешними телами при её переходе из одного состояния в другое, идёт на приращение внутренней энергии системы и на работу, которую система совершает при расширении:

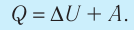
3.    При изохорном процессе всё передаваемое системе количество теплоты идёт на увеличение её внутренней энергии:

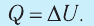
4.    При изотермическом процессе работа расширения или сжатия идеального газа сопровождается теплопередачей между газом и термостатом:

A=Q.

5.    При изобарном процессе переданное идеальному газу количество теплоты частично расходуется на увеличение внутренней энергии газа и частично идёт на совершение работы газом при его расширении:

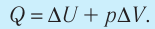
6.    При адиабатном процессе приращение внутренней энергии газа равно работе, которую совершает сила давления газа, взятой с противоположным знаком:

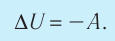
Пример №1

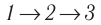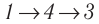Идеальный газ, масса которого постоянна, переводят из состояния / в состояние 3 двумя различными способами: и (рис. 70), где 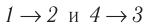— изотермы, а 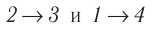— изохоры. Одинаковы ли при каждом переходе: а)    приращения внутренней энергии газа; б) работы, совершаемые силами давления газа; в) количества теплоты, сообщённые газу?

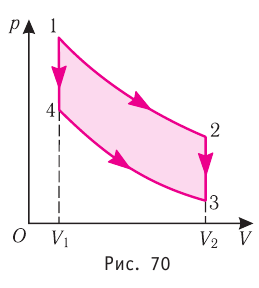
Решение, а) Так как начальное и конечное состояния для обоих переходов одинаковы, то будут одинаковы и приращения внутренней энергии:

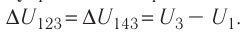
б)    Из рисунка 70 видно, что площадь фигуры, ограниченной осью OV, изотермой и изохорами, проходящими через точки 3 и 4, меньше площади фигуры, ограниченной осью ОV, изотермой и изохорами, проходящими через точки 1 и 2. Следовательно, в процессе перехода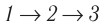 сила давления газа совершает большую работу, чем в процессе перехода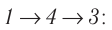

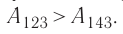
в)    Из первого закона термодинамики следует:

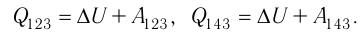
Поскольку приращения внутренней энергии в обоих случаях одинаковы, а совершённая силой давления газа работа больше при переходе 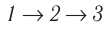, то количество теплоты, сообщённое газу, при переходе 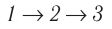также будет больше: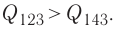

Ответ: а)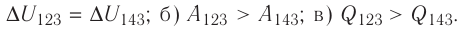

Пример №2

Идеальный одноатомный газ, давление которого 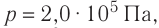, изобарно расширяется так, что его объём возрастает на 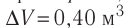. Определите приращение внутренней энергии газа и количество теплоты, получаемое газом в этом процессе.

Дано:

р = 2,0 • 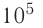Па

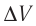=0,40 м3

р =const

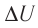— ? Q — ?
Решение. Приращение внутренней энергии идеального одноатомного газа 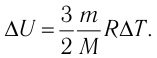При изобарном расширении идеального газа изменение его температуры 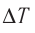связано с изменением объёма 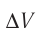газа соотношением 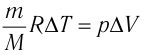(см. пример решения задачи после § 9). Тогда 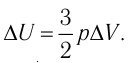Согласно первому закону термодинамики для изобарного процесса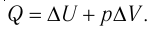

Отсюда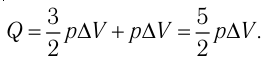

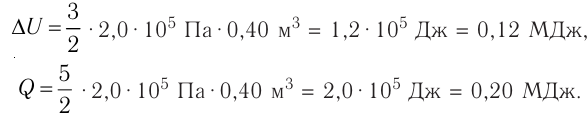
Ответ: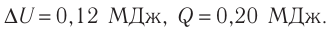 

Пример №3

В сосуд налита вода массой 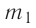= 800 г, температура которой 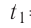= 60°С. В воду добавили некоторое количество льда при температуре 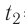= — 10 °С. Определите массу льда, если после достижения теплового равновесия температура содержимого сосуда 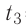=40°С. Теплоёмкостью сосуда можно пренебречь. Удельная теплоёмкость воды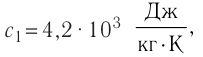льда —
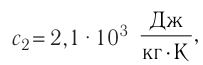удельная теплота плавления льда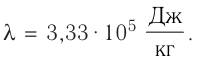

Дано

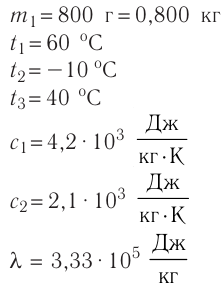
Решение. Если пренебречь потерями энергии в окружающую среду, то термодинамическая система «сосуд—вода—лёд» является изолированной. Поэтому учитываем только обмен энергией между входящими в систему телами при теплопередаче. Рассмотрим тепловые процессы, происходящие в системе: 1) нагревание льда от температуры 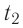до температуры плавления 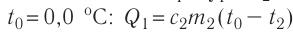; 2) плавление льда: 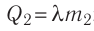, 3) нагревание холодной воды, получившейся при плавлении льда, от температуры 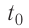до температуры 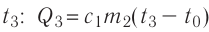; 4) охлаждение тёплой воды
массой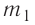 от температуры 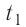до температуры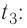

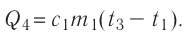Составим уравнение теплового баланса: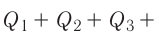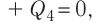или

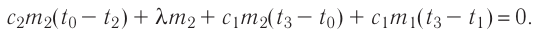
Отсюда масса льда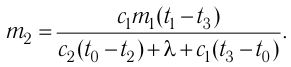

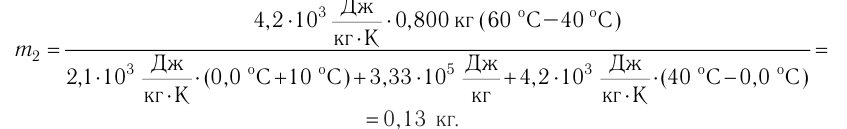
Ответ: 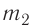= 0,13 кг.

Первый закон термодинамики

В 9-м классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия?

Закон сохранения энергии

В середине XIX в. известный английский физик Дж. Джоуль (1818—1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814—1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX в. Г. Гельмгольца (1821 — 1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы.

Закон сохранения и превращения энергии: при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.

Закон сохранения и превращения энергии является всеобщим законом природы и связывает воедино все физические явления. Этот закон выполняется абсолютно точно, на нём базируется всё современное естествознание.

Первый закон термодинамики:

В предыдущих параграфах мы рассматривали процессы, в которых внутренняя энергия системы изменялась или при совершении работы, или в результате теплообмена. Однако чаще всего при переходе системы из одного состояния в другое внутренняя энергия изменяется как за счёт совершения работы, так и за счёт теплообмена с окружающими телами.

Для термодинамических систем закон сохранения и превращения энергии называют первым законом термодинамики. 

Первый закон термодинамики: приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного (или отданного) системой при взаимодействии с внешними телами.

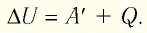
Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком 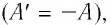то первый закон термодинамики можно сформулировать иначе:

Количество теплоты, полученное (или отданное) термодинамической системой при взаимодействии с внешними телами при её переходе из одного состояния в другое, идёт на приращение внутренней энергии системы и на работу, которую она совершает против внешних сил:

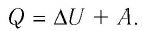
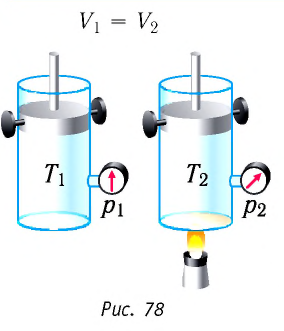
Применим первый закон термодинамики к различным изопроцессам изменения состояния идеального одноатомного газа.

Рассмотрим в качестве термодинамической системы идеальный одноатомный газ, находящийся в цилиндрическом сосуде, закрытом поршнем.

Изохорный процесс:

Если сосуд закрыт неподвижным поршнем, то при нагревании объём газа остаётся постоянным 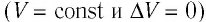(рис. 78). Следовательно, работа силы давления газа А = 0. Тогда первый закон термодинамики примет вид:

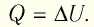
При изохорном процессе всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии:

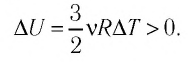
Если газ при изохорном процессе отдаёт количество теплоты, то его внутренняя энергия убывает: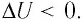

Изотермический процесс:

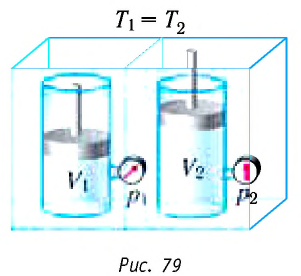
Поместим сосуд с газом, находящимся под подвижным поршнем, в термостат — устройство, в котором поддерживается постоянная температура (рис. 79). С помощью внешнего устройства медленно переместим поршень в сосуде так, чтобы объём газа увеличился (или уменьшился). Значения температуры газа в начальном и конечном состояниях одинаковы. В этом случае внутренняя энергия идеального одноатомного газа 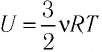остаётся постоянной, а её изменение 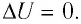Тогда первый закон термодинамики примет вид:

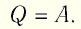
При изотермическом процессе переданное газу количество теплоты расходуется на совершение газом работы.

Изобарный процесс:

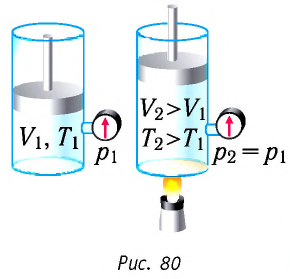
Если сосуд закрыт подвижным поршнем, то при нагревании увеличится как температура газа, так и его объём (рис. 80). Тогда первый закон термодинамики имеет вид:

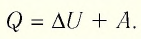
При изобарном процессе переданное газу количество теплоты частично расходуется на увеличение внутренней энергии системы и частично идёт на совершение работы силой давления газа при его расширении.

С учётом того, что при изобарном процессе работа расширения (сжатия) газа 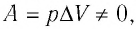первый закон термодинамики примет вид:

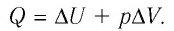
Пример №4

Идеальный одноатомный газ, давление которого 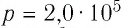 изобарно расширяется так, что его объём возрастает на 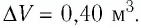Определите приращение внутренней энергии газа и количество теплоты, получаемое им в этом процессе.

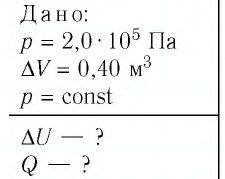
Решение. 11риращение внутренней энергии идеального одноатомного газа 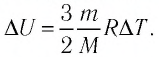При изобарном расширении идеального газа изменение его температуры  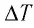связано с изменением объёма 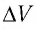газа соотношением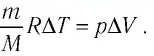

Тогда 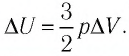Согласно первому закону термодинамики для изобарного процесса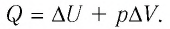

Следовательно,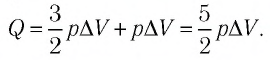

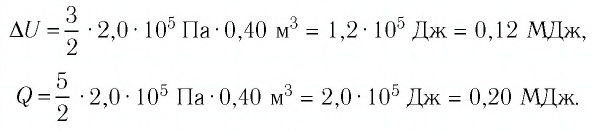
Ответ: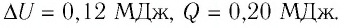

Пример №5

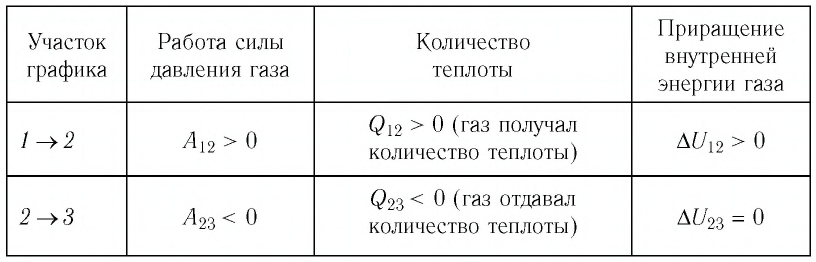
На рисунке 81 представлен график процесса изменения состояния некоторой массы идеального газа (участок 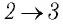 — изотерма). На каком участке графика работа силы давления газа: а) положительная; б) отрицательная? На каком участке графика газ: а) получал количество теплоты; б) отдавал? Как изменялась внутренняя энергия газа?

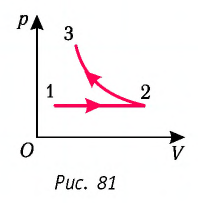
Решение. Участок 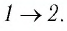Поскольку при постоянном давлении 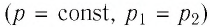увеличивается объём газа 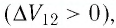то растёт и его температура 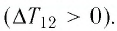Следовательно, работа силы давления газа 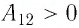и приращение его внутренней энергии 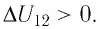Из первого закона термодинамики, записанного в виде 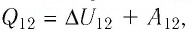следует, что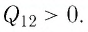

Участок 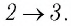Поскольку температура газа не изменяется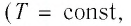 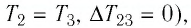то приращение его внутренней энергии 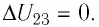Объём газа уменьшается (изотермическое сжатие), и работа силы давления газа 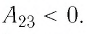Из первого закона термодинамики, записанного в виде 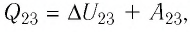дует, что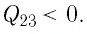

Ответ:

Определение первого закона термодинамики

Невозможно представить себе повседневную жизнь без разноцелевой техники, облегчающей нашу жизнь. При помощи этой техники люди вспахивают землю, добывают нефть, газ, руду и другие полезные ископаемые, "сокращают" большие расстояния и т.д. Главное свойство всей техники - способность совершения ими работы.

По этой причине еще с древних времен люди пытались создать способный работать вечно perpetuum mobile, то есть вечный двигатель. Как одну из интересных работ в этом направлении можно показать оригинальный проект, предложенный английским священником Джоном Уилкенсином в XVII веке, основанный на действии магнитного поля. По идее проекта, вечный двигатель должен работать так: шарообразный магнит помещен на высокую опору, к которой прикрепляются две наклонные плоскости, верхняя плоскость прямолинейная, а нижняя изогнутая (а).

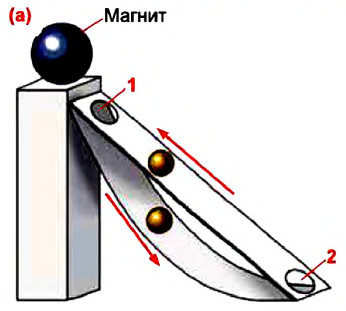
В результате притяжения магнитом шарик, помещенный в нижней части прямой плоскости, начинает подниматься вверх и проваливается на нижнюю плоскость через отверстие 1 в верхней части плоскости. Затем, скатываясь вниз по изогнутой плоскости, снова попадает на прямую плоскость через отверстие 2, и всё повторяется снова.

Первый закон термодинамики:

Согласно одному из фундаментальных законов природы - закону сохранения энергии, полная энергия (механическая и внутренняя энергия) замкнутой системы остается постоянной при всех процессах, происходящих внутри этой системы:

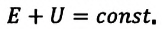
Закон сохранения энергии, применяемый к тепловым процессам, называют первым законом термодинамики:

Изменение внутренней энергии термодинамической системы равно количеству теплоты, переданному этой системе, и работе внешних сил, совершенной над системой:

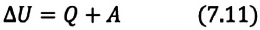
Над замкнутой и изолированной системой внешние силы не совершают работу 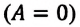и не происходит теплообмена с окружающими телами 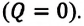В этом случае, согласно первому закону термодинамики, внутренняя энергия замкнутой и изолированной системы не изменяется:

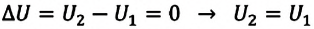
Так как работа, совершаемая системой над внешними силами, равна работе, совершаемой внешними силами над системой с противоположным знаком: 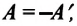то первый закон термодинамики можно записать так:

Количество теплоты, сообщенное термодинамической системе, затрачивается на изменение ее внутренней энергии и работу, которую система совершает против внешних сил:

После открытия закона сохранения энергии стала очевидной невозможность создания вечного двигателя первого рода:

Вечный двигатель первого рода (perpetuum mobile I) - это двигатель, который будучи однажды приведен в действие и не получая энергию извне, совершает работу вечно.

Согласно выражению (7.11), для совершения работы система или должна получать энергию извне, или использовать свою внутреннюю энергию:

В противном случае, то есть есл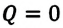и и 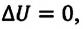то и работа 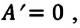а это означает, что работающий вечный двигатель невозможен.

Применение первого закона термодинамики к разным процессам

1. Изотермический процесс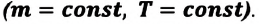 

Так как в этом процессе температура системы остается постоянной, то и ее внутренняя энергия остается постоянной, изменение же внутренней энергии равно нулю:

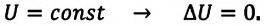
Из выражений первого закона термодинамики (7.11) и (7.12) получаем:

• При изотермическом процессе все количество теплоты, переданное системе, затрачивается на совершение работы.

2. Изохорный процесс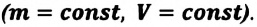

Так как в этом процессе объем системы остается постоянным, то из выражения (7.10) следует, что работа не совершается 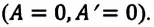Первый закон термодинамики приобретает вид:

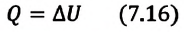
Для одноатомного идеального газа:

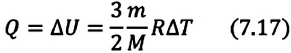
• При изохорном процессе количество теплоты, переданное системе, целиком затрачивается на изменение внутренней энергии.

Удельная теплоемкость одноатомного идеального газа, при постоянном объеме

Если в выражении (7.17) учесть выражения внутренней энергии одноатомного идеального газа (7.7) и количества теплоты (7.4), то получим формулу для удельной теплоемкости при постоянном объеме:

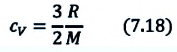
3. Изобарный процесс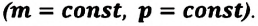 

В этом процессе давление системы остается постоянным, а температура и объем изменяются. Для этого процесса первый закон термодинамики записывается, так: 

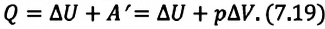
• При изобарном процессе (расширении) переданное системе количество теплоты затрачивается на увеличение его внутренней энергии и на совершение газом работы против внешних сил.

Удельная теплоемкость одноатомного идеального газа при постоянном давлении

Приняв в (7.19) во внимание выражения для одноатомного идеального газа:

получим:

С учетом этих выражений можно определить удельную теплоемкость одноатомного идеального газа при постоянном давлении как:

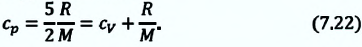
Из сравнения выражений (7.20) и (7.21) видно, что при изобарном процессе для одноатомного идеального газа существуют следующие соотношения между переданным количеством теплоты, изменением внутренней энергии и совершенной работой:

4. Адиабатный процесс

Адиабатный процесс - это процесс, происходящий без теплообмена системы с окружающей средой.

Так как в этом процессе отсутствует теплообмен системы со сторонними телами, то первый закон термодинамики можно записать так:

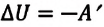
или

При адиабатном расширении газа его температура и внутренняя энергия уменьшаются, то есть газ охлаждается, а при адиабатном же сжатии, наоборот, его температура и внутренняя энергия увеличиваются, то есть газ нагревается.

История первого закона термодинамики

Один из фундаментальных законов природы — закон сохранения и превращения энергии. Первым этот закон сформулировал немецкий врач и физик Юлиус Роберт фон Майер (1814–1878). интересно, что к открытию ученого подтолкнули наблюдения над цветом крови у людей. Майер заметил, что венозная кровь у жителей тропиков светлее, чем у жителей его страны, и по цвету напоминает артериальную. он сделал вывод, что разница в цвете обусловлена количеством потребления кислорода, или «силой процесса сгорания», происходящего в организме. независимо от Майера и совсем иначе к открытию закона сохранения энергии пришли английский промышленник и ученый Джеймс Прескотт Джоуль (1818–1889) и немецкий физик, физиолог и психолог Герман Людвиг Фердинанд фон Гельмгольц (1821–1894). закон сохранения и превращения энергии управляет всеми явлениями природы, неизвестно ни одного случая, когда бы этот закон не выполнялся.

В термодинамике рассматривают системы, механическая энергия которых при переходе из одного термодинамического состояния в другое не изменяется. Тогда, если внешние силы совершили работу A′ и одновременно системе передано определенное количество теплоты Q, вся энергия идет на изменение внутренней энергии системы (∆U) . Закон сохранения и превращения энергии в таком случае называют первым законом (началом) термодинамики:

Изменение внутренней энергии системы ( ∆U) при переходе из одного термодинамического состояния в другое равно сумме работы A′ внешних сил и количества теплоты Q, сообщенного системе или переданного системой окружающим телам в процессе теплообмена:

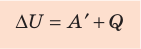
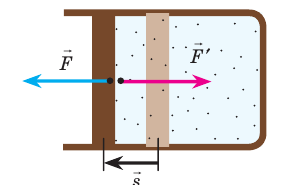
Рис. 38.1. согласно третьему закону ньютона сила 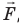, с которой газ давит на поршень, равна по модулю и противоположно направлена внешней силе 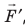, с которой поршень давит на газ. Поэтому работа внешних сил равна работе газа, взятой с противоположным знаком: A = −A ′

Обратите внимание! Если система получает некоторое количество теплоты, то в приведенной формуле Q берется со знаком «+», если отдает, то со знаком «–». На практике чаще рассматривают не работу A′ внешних сил, а работу A совершаемую данной системой против внешних сил. Учитывая, что A = −A ′ (рис. 38.1), первый закон (начало) термодинамики можно сформулировать так:

Количество теплоты Q, переданное системе, идет на изменение внутренней энергии системы (∆U) и на совершение системой работы A против внешних сил:

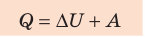
Согласно первому закону термодинамики невозможно создать вечный двигатель первого рода — циклическое устройство, которое совершало бы механическую работу без потребления энергии извне (рис. 38.2, а) или совершало бы работу большую, чем потребляемая им энергия (рис. 38.2, б).

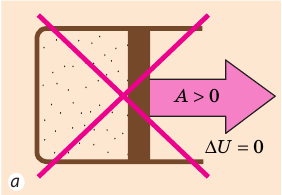
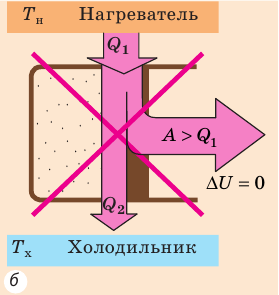
Рис. 38.2. Циклические процессы, которые невозможны с точки зрения первого закона термодинамики

Какой вид имеет первый закон термодинамики для изопроцессов

Рассмотрим, какой вид принимает первый закон термодинамики в случаях, когда идеальному газу неизменной массы передают некоторое количество теплоты таким образом, что один из макроскопических параметров газа (V, p или T) остается неизменным.

• Изохорный процесс (рис. 38.3). В ходе изохорного процесса объем газа не изменяется (∆V=0) и газ работу не совершает (A = 0), поэтому уравнение первого закона термодинамики имеет вид: Q=∆U . При изохорном процессе все переданное газу количество теплоты расходуется на увеличение внутренней энергии газа. Если идеальный газ одноатомный, то количество теплоты, переданное газу, равно:
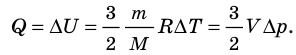
• Изотермический процесс (рис. 38.4). В ходе изотермического процесса температура, а значит, и внутренняя энергия газа не изменяются (∆U=0), поэтому уравнение первого закона термодинамики имеет вид: Q=A.

При изотермическом процессе все переданное газу количество теплоты идет на совершение механической работы.

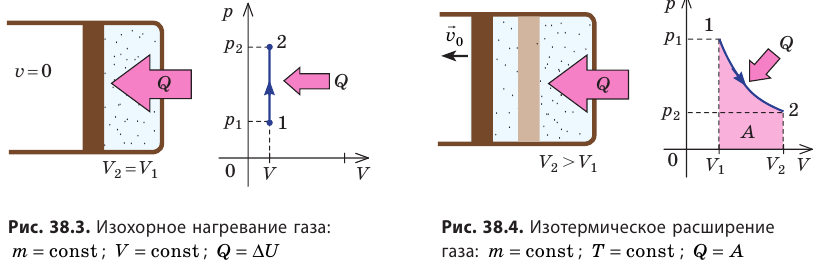
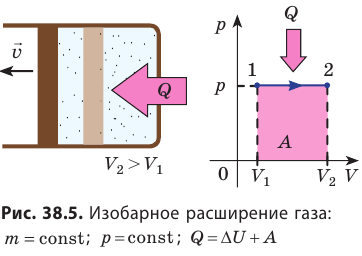
• Изобарный процесс (рис. 38.5). В ходе изобарного процесса совершается работа и изменяется внутренняя энергия газа, поэтому уравнение первого закона термодинамики имеет вид: Q=∆U + A. При изобарном процессе переданное газу количество теплоты идет и на увеличение внутренней энергии газа, и на совершение механической работы. Если идеальный газ одноатомный, то работа газа A=p∆V, изменение его внутренней энергии 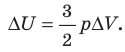Количество теплоты, переданное газу, равно: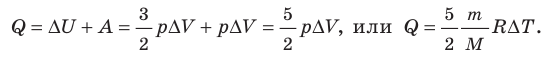

Каковы особенности адиабатного процесса

Адиабатный процесс — это процесс, который происходит без теплообмена с окружающей средой. При адиабатном процессе количество теплоты Q, переданное системе, равно нулю, поэтому первый закон термодинамики имеет вид: Q=∆U + A, или A = −∆U.

При адиабатном расширении газ совершает положительную работу за счет уменьшения внутренней энергии; температура газа уменьшается.

Поскольку p =nkT, при адиабатном сжатии давление газа возрастает намного быстрее, чем при изотермическом, ведь одновременно с увеличением концентрации молекул газа увеличивается и его температура (рис. 38.6).

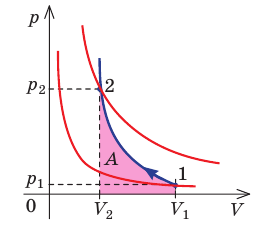
Рис. 38.6. изменение давления газа в ходе адиабатного сжатия. синим цветом показана адиабата, красным — изотермы

Аналогично при адиабатном расширении давление падает быстрее, чем при изотермическом, ведь одновременно уменьшаются и концентрация, и температура газа.

В реальных условиях процесс, близкий к адиабатному, можно осуществить, если газ будет находиться в оболочке с очень хорошими термоизоляционными свойствами. Адиабатными можно считать и процессы, которые происходят очень быстро: в таком случае газ не успевает обменяться теплотой с окружающей средой (например, расширение и сжатие воздуха при распространении звуковых волн, расширение газа при взрыве).

Увеличение температуры при резком сжатии воздуха используется в дизельном двигателе, в котором нет системы зажигания горючей смеси.

Пример №6

При изобарном расширении неон совершил работу 56 Дж. Какое количество теплоты передано газу? Каково изменение его внутренней энергии? При каком давлении происходил процесс, если объем газа увеличился на 2,0 л?

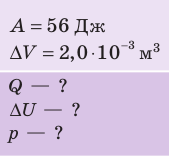
Решение:

Для изобарного процесса работа газа равна: A=p∆V. Отсюда 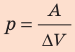. Изменение внутренней энергии идеального одноатомного газа равно: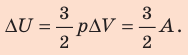

Согласно первому закону термодинамики: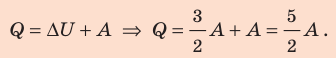 Проверим единицу, найдем значения искомых величин

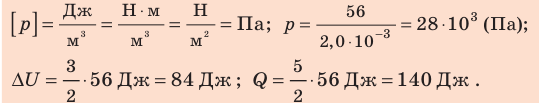
Ответ: Q = 140 Дж; ∆U = 84 Дж; p = 28 кПа.

Выводы:

• Закон сохранения энергии, записанный для тепловых процессов, называют первым законом (началом) термодинамики: количество теплоты, переданное системе, идет на изменение внутренней энергии системы и на совершение системой работы против внешних сил: Q=∆U + A.
• При изохорном процессе газ не выполняет работу (A = 0 ) , поэтому вся теплота, переданная газу, идет на увеличение его внутренней энергии: Q=∆U.
• При изотермическом процессе внутренняя энергия газа не изменяется (∆U=0), поэтому вся теплота, переданная газу, идет на совершение газом работы: Q=A.
• При изобарном процессе теплота, переданная газу, идет как на увеличение внутренней энергии газа, так и на совершение газом работы: Q=∆U + A.
• При адиабатном процессе газ не получает теплоты (Q = 0) , поэтому увеличение его внутренней энергии происходит за счет совершения над газом работы (адиабатное сжатие): ∆U=A′. Если газ сам совершает работу (адиабатное расширение), его внутренняя энергия уменьшается: A = −∆U.