Первый признак равенства треугольников - определение и вычисление с примерами решения

Первый признак равенства треугольников:

Докажем первый признак равенства треугольников.

Теорема (первый признак равенства треугольников). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Доказательство.

Пусть ABC и A₁B₁C₁  — треугольники, у которых AB =A₁B₁, AC = A₁C₁ и 

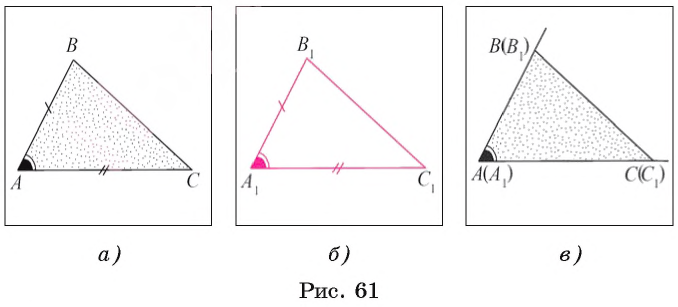
1. Отложим B₁A₁C₁ в той же полуплоскости с границей АС, в которой лежит угол ВАС, так, чтобы сторона A₁C₁  совпала со стороной АС. Это возможно в силу аксиомы откладывания отрезка на луче и условия АС= A₁C₁ .
2. Так как BAC = B₁A₁C₁ , то, согласно аксиоме откладывания угла в полуплоскость, лучи АВ и A₁B₁ совпадут.
3. Так как АВ = A₁B₁ , то по аксиоме единственности откладывания отрезка на луче точка B₁  совпадет с точкой B, кроме того, точка С совпадает с точкой C₁ . С учетом того, что через две точки проходит единственная прямая, получаем, что отрезки ВС и B₁C₁  совпадают. Таким образом, совпадают углы и стороны треугольников ABC и A₁B₁C₁ , значит, эти треугольники равны (рис. 61, в).

Теорема доказана.

Пример:

Отрезки АD и СB пересекаются в точке О. Известно, что АО = СО и ВО = DО. Докажите, что треугольник АОВ равен треугольнику СОD.

Доказательство.

Для доказательства равенства треугольников АОВ и СОD воспользуемся первым признаком равенства треугольников. По условию задачи АО = СО и ВО = ВО (рис. 62, а, б). Кроме того, АОВ = СОD,

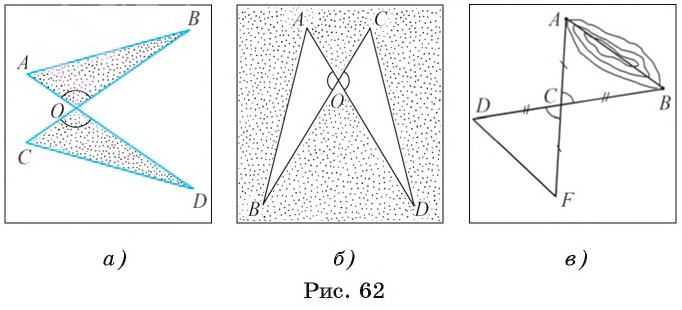
так как они являются вертикальными. Таким образом, две стороны АО, ВО и угол между ними АОВ треугольника АОВ соответственно равны двум сторонам СО, DO и углу COD между ними треугольника COD. Следовательно, по первому признаку равенства треугольников АОВ = COD.

Что и требовалось доказать.

Первый признак равенства треугольников можно применять при решении задач практического характера. Рассмотрим пример решения такой задачи.

Пример:

Пусть нам необходимо измерить расстояние между точками А и В на берегах озера, между которыми нельзя пройти по прямой (рис. 62, в).

Для этого выберем какую-нибудь точку С, для которой можно измерить расстояния АС и СВ. Затем отметим еще две точки D и F так, чтобы точка С оказалась общей серединой отрезков AF и BD. Тогда расстояние между точками F и D равно искомому расстоянию. Действительно, треугольники АСВ и FCD равны, так как AC = CF и BC = CD по построению, а ACB = FCD, так как они являются вертикальными. Следовательно, DF = АВ.