Перспектива в начертательной геометрии с примерами

Содержание:

Перспективной проекцией (перспективой) называется центральная проекция пространственного объекта на специально выбранную поверхность. Само слово «перспектива» происходит от латинского глагола «рег-spicere» - «видеть насквозь».

Перспектива является одним из методов построения наглядных изображений пространственных предметов.

В зависимости от того, на какой поверхности строят перспективу, различают следующие ее виды

1. линейная перспектива - изображение на плоскости;
2. панорамная перспектива - изображение на цилиндрической поверхности;
3. купольная перспектива - изображение на сферической поверхности.

В данной лекции рассматривается линейная перспектива.

Получение перспективного изображения можно представить следующим образом Если пучок лучей, идущих от глаза наблюдателя по направлению к предмету, пересечь плоскостью, то полученное сечение будет перспективным изображением предмета. Перспектива подчиняется законам и правилам, по которым можно изображать предметы так, как они представляются нашему глазу в пространстве.

Система проецирования для построения перспективного изображения включает в себя следующие элементы (рис. 15.1):

• - предметная плоскость
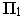
• - картинная плоскость 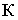 или картина - перпендикулярна предметной плоскости, служит для получения на ней перспективного изображения;

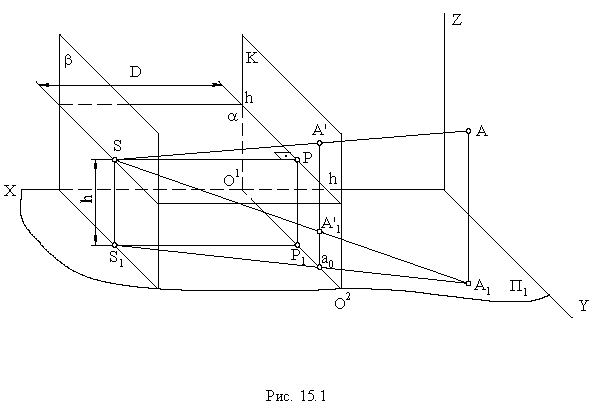
• -    основание картины - линия пересечения картинной и предметной плоскостей, обозначается 
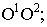
• -    центр проекций 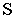 - точка, в которой располагается плаз наблюдателя; называется точкой зрения;
• - точка стояния 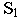 - проекция точки зрения на предметную плоскость; называется основанием точки зрения;
• - главный луч 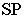 - перпендикуляр, опущенный из точки зрения  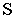на картинную плоскость  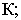длина его называется главным расстоянием;
• - главная точка картины 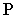 - точка пересечения главного луча с картиной;
• -  основание главной точки картины 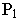 - проекция главной точки  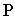на предметной плоскости;
• -  центральная линия картины 
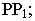
• - плоскость горизонта 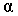 - горизонтальная плоскость, проходящая через точку зрения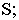 
• - линия горизонта 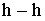 - линия пересечения плоскости горизонта с картинной плоскостью;
• - нейтральная плоскость 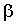 - плоскость, проходящая через точку зрения  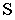параллельно картинной плоскости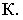 

Картинная и нейтральная плоскости делят все пространство на три части:

• - предметное пространство, которое находится за картинной плоскостью, в котором располагаются проецируемые предметы;
• - промежуточное пространство - между картинной и нейтральной плоскостями;
• - мнимое пространство, расположено по другую сторону от нейтральной плоскости.

Горизонтальные проекции точек на предметную плоскость 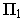 называются основаниями этих точек н обозначаются так же, как горизонтальные проекции точек в ортогональных проекциях:  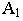- основание точки  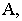расположенной в предметном пространстве.

Перспектива точки

Для того чтобы построить перспективу точки 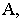 расположенной в предметном пространстве (см рис. 15.1), необходимо из точки зрения  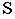провести луч через точку  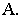Точка пересечения этого проецирующего луча  с картинной плоскостью 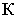 определит перспективу точки  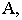т.е. точку  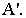Аналогично можно найти и перспективу основания точки  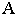- перспективу  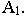Точка пересечения луча  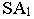с картинной плоскостью определит перспективу точки  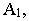т.е. точку  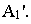Точка 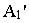 называется перспективой основания точки  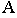или вторичной перспективной проекцией точки  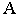(первичной проекцией считается ортогональная проекция этой точки -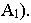 

Для того чтобы обеспечить взаимно-однозначное соответствие между точками пространства и их перспективными проекциями, строят на картинной плоскости перспективную проекцию точки 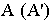 и ее вторичную проекцию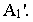 

Таким образом, положение точки в пространстве может быть определено, если на изображении заданы перспективы точки 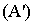 и ее основания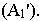 

Перспектива прямой

Перспективой прямой линии является прямая. Для построения перспективы заданного прямолинейного отрезка необходимо построить перспективы двух его точек. Представим бесконечную прямую, заданную отрезком 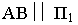 (рис. 15.2). В перспективном изображении прямая имеет две характерные точки - начальную и конечную. Начальная точка  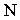является следом прямой на картинной плоскости  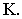Для того чтобы найти конечную точку  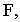построим изображение в перспективе промежуточных точек прямой.

Возьмем на заданной прямой несколько точек - 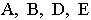 и т. д. Проведя лучи от точки зрения  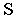к каждой точке прямой, видим, что чем дальше точка прямой  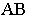от картины, тем острее угол, образуемый лучом с этой линией. Постепенно лучи будут приближаться к положению, параллельному данной прямой.

Луч. проведенный в точку на прямой, удаленную на бесконечно большое расстояние от картины, пройдет параллельно самой прямой и пересечет картину в точке 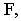 расположенной на линии горизонта. Прямая  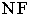будет полной перспективой рассматриваемой прямой  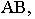параллельной предметной плоскости. Точка  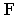на линии горизонта называется точкой схода. Лучи  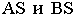ограничивают на полной перспективе прямой перспективное изображение  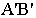отрезка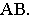 

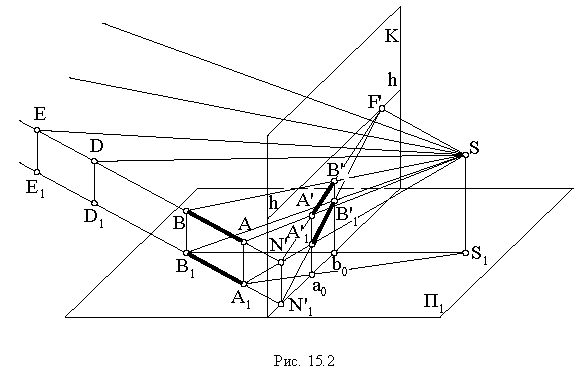
Можно для получения перспективного изображения отрезка 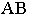 воспользоваться горизонтальными проекциями лучей  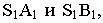которые в пересечении с основанием картины дадут точки  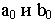(картинные следы). Проведя перпендикуляры к основанию картины через эти точки, найдем на пересечении с полной перспективой прямой точки  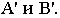Для того чтобы перспективное изображение прямой было однозначно обратимым, необходимо перспективу  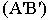прямой  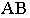дополнить перспективой  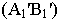ее горизонтальной проекции  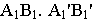называется вторичной проекцией.

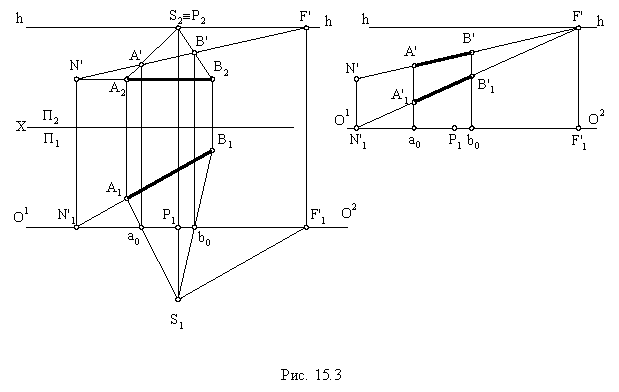
На рис. 15.3 построена полная перспектива прямой, параллельной плоскости 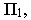 заданной отрезком  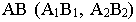на ортогональном чертеже. Горизонтальный след  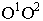картины намечаем между горизонтальной проекцией отрезка  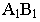и точкой стояния  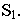Проводим линию горизонта  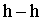и переносим на неё точку зрения  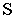и главную точку картины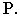 

Создав таким образом систему проецирования, строим перспективу прямой Начальную точку 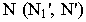 находим, продолжая прямую в сторону картинной плоскости. Конечную точку или точку схода  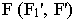получим, проведя луч 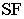параллельно  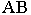до пересечения с картинной плоскостью в точке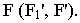 

Чтобы получить перспективу 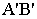 отрезка  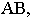необходимо провести проецирующие лучи  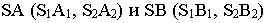и найти точки их пересечения с картиной. Построение вторичной проекции  показано на чертеже (см. рис. 15.3).

Приведем некоторые свойства прямых в перспективе:

• -    линии, параллельные между собой в пространстве, имеют в перспективе общую точку схода;
• -    линии, принадлежащие картинной плоскости, сохраняют в перспективе натуральную величину;
• -    горизонтальные прямые, не параллельные картинной плоскости, имеют точки схода на линии горизонта;
• -    горизонтальные прямые, расположенные под углом 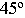 к картине, имеют точку схода, лежащую на линии горизонта и удаленную от главной точки картины  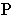на величину главного расстояния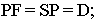 
• -    точкой схода горизонтальных прямых, перпендикулярных картине, является главная точка картины 
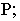
• -    перспективы прямых, принадлежащих предметной плоскости 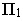 и проходящих через основание точки зрения, перпендикулярны основанию картины  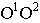и линии горизонта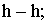 
• -    перспективы прямых, параллельных картине, параллельны самим прямым. Отсюда следует, что вертикальные прямые изображаются в перспективе вертикальными прямыми.

Перспектива плоских фигур

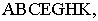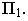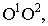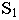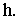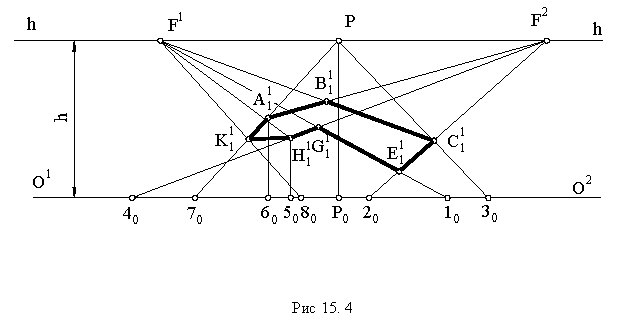
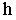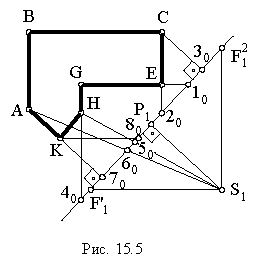
Построим перспективу фигуры  принадлежащей плоскости Положение картинной плоскости определено ее основанием  положение точки зрения - точкой  и высотой горизонта  Проведем линию горизонта и основание картины на заданном расстоянии  (рис. 15.4), определим положение точки 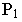 в плане (рис. 15.5) и отметим ее в перспективе.

Фигура 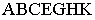 ограничена, в основном, двумя группами параллельных линий. Одно из доминирующих направлений определяется прямыми  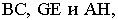другое - прямыми  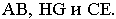Определим для них точки схода  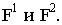Построим в перспективе на линии горизонта точк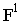и  и 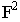 на соответствующих расстояниях от точки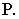 

Начнем построение перспективы с точки 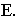 Продолжим прямые  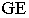и 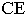 до основания картины и отметим точки  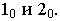Перспектива прямой  проходит через точки 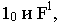 прямой  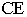 - через точки  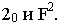На пересечении этих прямых расположена перспектива точки  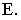Точка 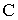 лежит на прямой перспектива которой уже построена. Поэтому проведем через точку  еще одну прямую, например, перпендикулярную основанию картины. Она пересекается с основанием картины в точке 

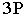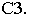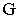Построим перспективу  прямой  Точка  лежит на пересечении прямых  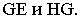Для построения ее перспективы нужно построить только перспективу прямой  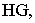так как перспектива прямой  уже найдена. Отметив точку 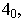 проведем через эту точку и  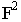перспективу прямой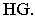 

Найдем перспективу точки 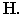 Воспользуемся, например, прямой, проходящей через эту точку и точку  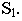Перспектива такой прямой идет через точку  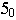вертикально. В ее пересечении с перспективой  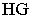отметим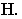 

Перспектива точки 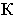 построена с помощью горизонтальных прямых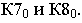 

Проводим перспективы прямых 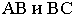 соответственно через точки  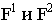и получаем перспективу точки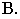 

Перспектива точки 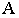 построена с помощью прямой  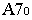и прямой, проходящей через точку  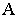и точку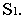 

Выбор прямых, с помощью которых строятся перспективы точек фигуры, зависит от конкретных условий задачи. В данном примере были использованы три типа горизонтальных прямых: 1) проходящих через точку 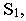 2) перпендикулярных основанию картины, 3) наклоненных к основанию картины

Рассмотрим построение перспективы окружности (рис. 15.6, а, б). В перспективе изображение окружности строят чаще всего, вписывая ее в квадрат (в перспективное изображение квадрата). Расположим картинную плоскость фронтально. Тогда перспективы прямых 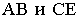 будут иметь точкой схода главную точку картины  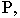так как  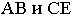перпендикулярны картине. Перспективу окружности, вписанной в квадрат, можно построить по восьми точкам. В четырех точках она касается сторон квадрата, а другие ее четыре точки располагаются на его диагоналях. В связи с тем, что диагонали располагаются под углом  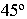к плоскости картины, точками их схода будут являться точки дальности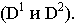 

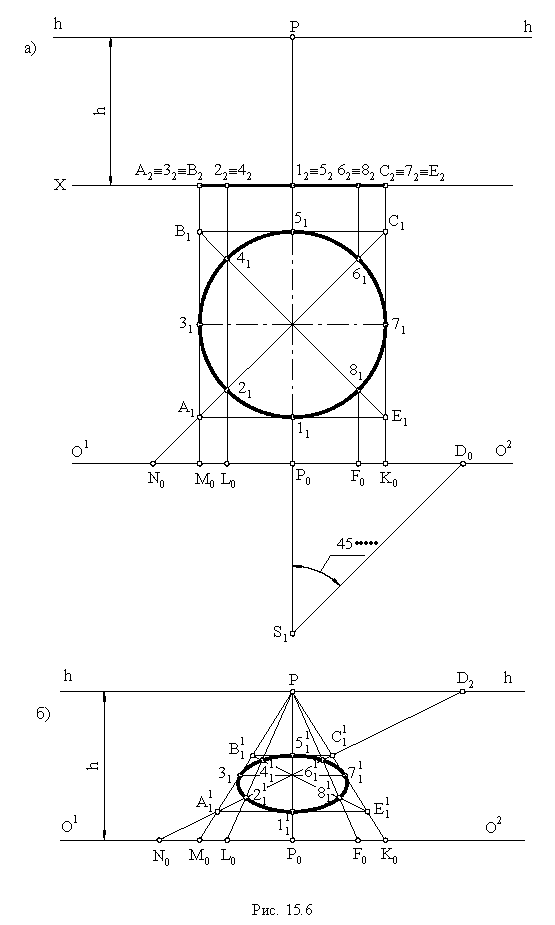
Способы построения перспективных изображений

Построение перспектив в строительном черчении и начертательной геометрии производится по прямоугольным проекциям. В качестве таких проекций здания выбирают его горизонтальную и фронтальную проекции, которые называют планом и фасадом.

Существует несколько способов построения перспектив геометрических тел и зданий по заданному чертежу в прямоугольных проекциях. Рассмотрим некоторые из них, имеющие наиболее широкое практическое применение.

Способ перспективных координат, разработанный Н.Л. Русскевичем, в литературе называют «способом ортогонального эпюра».

Суть способа состоит в использовании прямоугольных проекций предмета для графического определения двух координат перспективы точки. Он отличается простотой и компактностью построения за счет отказа от использования точек схода.

Этот способ заключается в том, что на картинной плоскости выбирается новая система координат 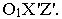 За ось  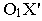принимается основание картины  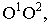начало координат  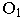выбирается в произвольной точке (рис. 16.1, а). Перспектива точки  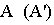на ортогональном эпюре определяется как след луча, т.е. как точка пересечения луча  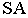с плоскостью  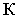(точка  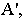ее проекции  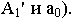В новой системе координат  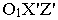на плоскости  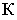определяются координаты точки  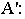координата  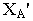и координата  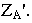Эти координаты в выбранном масштабе откладываются на картине  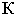и определяют положение перспективы точки  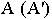(см. рис. 16.1, б и в).

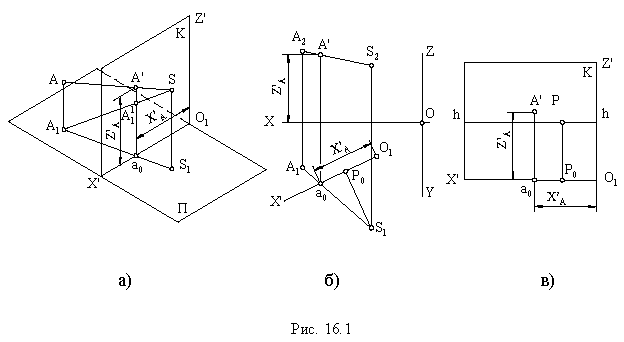
На рис. 16.2 показано построение перспективы сооружения способом перспективных координат (перспективное изображение увеличено в два раза по сравнению с ортогональными проекциями).

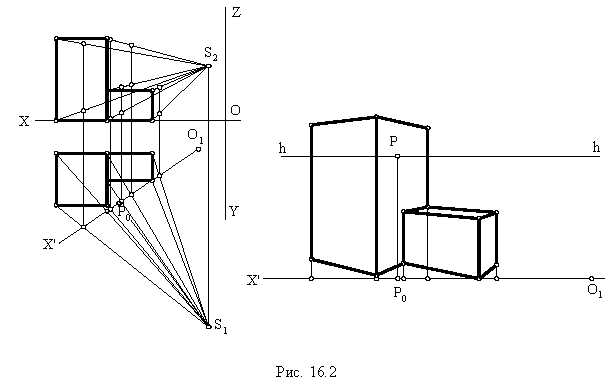
Способ архитекторов. В основу этого способа положено свойство параллельных прямых сходиться в перспективе в одной точке (точке схода  Этот способ применяется при построении перспективных изображений различных сооружений, которые в плане имеют два доминирующих направления линий.

Рассмотрим последовательность построения перспективы здания способом архитекторов. Для получения более выразительной перспективы след картинной плоскости проводим через одни из углов здания и располагаем под углом 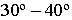 к направлению главного фасада. Точку зрения выбираем так, чтобы угол зрения, определяемый крайними лучами зрения, был равен  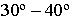и чтобы она лежала на перпендикуляре, восстановленном в средней третьей части ширины картины (рис. 16.3).

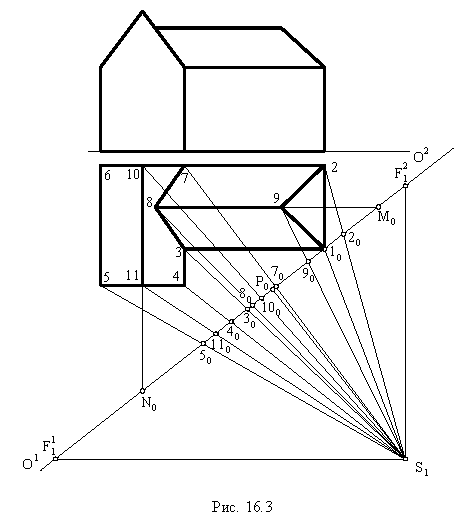
Точки схода для основных направлений плана найдутся, если провести прямые из точки 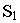 параллельно сторонам объекта до пересечения с основанием картины в точках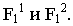 

После установки точки зрения, картинной плоскости и нахождения точек схода проводятся лучи зрения из всех точек объекта и на следе картинной плоскости 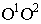 фиксируются все точки пересечения:  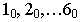и т.д.

Для построения самой перспективы переносим след картинной плоскости со всеми нанесенными на нем точками, линию горизонта, главную точку картины и точки схода 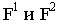 на то пространство, где будем строить перспективу (рис. 16.4). Линию горизонта проводим параллельно основанию картинной плоскости  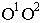на заданной высоте и на нее переносим точки схода с основания картинной плоскости.

Так как картинная плоскость проведена через ребро 1, то оно в перспективе изобразится в натуральную величину. Из точки 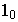 восстанавливаем перпендикуляр к следу картинной плоскости н на нем откладываем высоту ребра 1, взятую с фронтальной проекции ортогонального чертежа. Нижнюю и верхнюю точки ребра 1 соединяем с точками схода  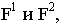получая направление сторон здания Восстановив перпендикуляры из точек  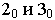до пересечения с лучами, идущими в точки схода, получим стороны здания 1-2 и 1-3. Таким же образом находим все ребра и стороны объекта в перспективе.

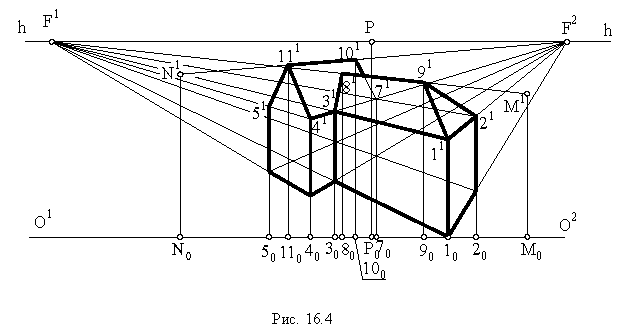
Для получения точек 8, 9, 10 и 11 в перспективе продолжим линию конька 11-10 до пересечения с картинной плоскостью 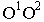 в точке  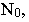а линию 8-9  до пересечения в точке  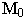и переносим эти точки в перспективу. Из полученных точек восстанавливаем перпендикуляры, на которых откладываем высоты от земли до соответствующего конька. Соединяем точки  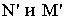точками схода и, пересекая полученные линии перпендикулярными прямыми, восстановленными из точек  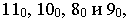получим перспективное изображение прямых 11-10 и 8-9, принадлежащих конькам кровли. Найденные точки соединяем с соответствующими точками, согласно ортогональному чертежу, и получаем перспективное изображение кровли.

Выбор рационального положения картины и точки зрения при построении перспективы

Наглядность перспективных изображений зависит от правильности выбора положения картины и точки зрения

Основание картинной плоскости 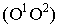 должно составлять с одной из сторон плана сооружения (чаще всего с главным фасадом) угол  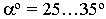(рис. 16.5). Картинную плоскость обычно совмещают с одним из вертикальных ребер изображаемого объекта.

Точка зрения должна быть расположена так, чтобы соблюдались следующие условия:

1. Угол зрения 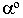 должен быть в пределах  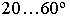(наиболее наглядное перспективное изображение получается при угле зрения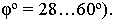 
2. Главная точка картины 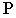 должна находиться в средней трети ширины изображаемого объекта (т.е. в средней трети отрезка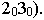 

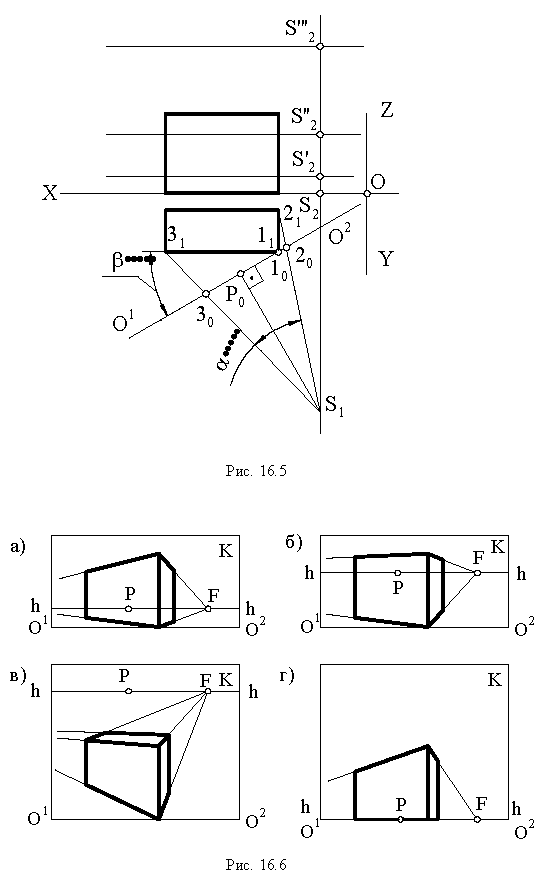
Вид перспективного изображения зависит от высоты горизонта.

Перспектива, полученная с точки зрения 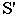 (рис. 16.6), расположенной на высоте человеческого роста (1,5... 1,7 м), называется перспективой с нормального горизонта (см. рис. 16.6, а).

Если точка зрения 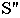 (см рис. 16.5) находится выше человеческого роста, в пределах средней трети высоты сооружения, то перспективу называют перспективой с повышенного горизонта (см. рис. 16.6, б).

Если точка зрения 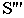 (см. рис. 16.5) располагается выше изображаемого объекта, на высоте 100 метров и выше, тогда перспективу называют перспективой с птичьего полета (см. рис. 16.6, в).

Перспективой с нулевого горизонта (см рис. 16.6, г) называется перспективное изображение при расположении точки зрения на предметной плоскости 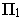 (точка  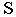на рис. 16.5).