
Перпендикулярные прямые в геометрии с примерами
Определение: Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
При пересечении двух перпендикулярных прямых образуются 4 прямых угла.
Отрезки и лучи называются перпендикулярными, если они лежат на перпендикулярных прямых. На рисунке 87 прямые 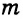
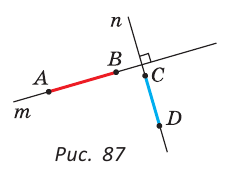
Определение. Перпендикуляром к данной прямой называется отрезок, который лежит на прямой, перпендикулярной данной, один из концов которого (основание перпендикуляра) является точкой пересечения этих прямых.
Прямая 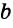 перпендикулярна прямой
перпендикулярна прямой 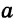 (рис. 88). Отрезок АВ — перпендикуляр к прямой
(рис. 88). Отрезок АВ — перпендикуляр к прямой 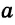 , точка В — основание перпендикуляра. Точку В также называют проекцией точки А на прямую
, точка В — основание перпендикуляра. Точку В также называют проекцией точки А на прямую  .
.
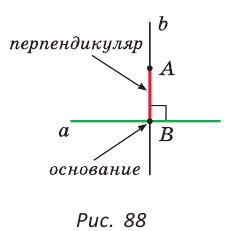
Если из точки М, которая не лежит на прямой  , провести перпендикуляр МК к прямой
, провести перпендикуляр МК к прямой  (рис. 89), то получим перпендикуляр, опущенный из точки М на прямую
(рис. 89), то получим перпендикуляр, опущенный из точки М на прямую  . Если из точки Р, лежащей на прямой
. Если из точки Р, лежащей на прямой  , провести перпендикуляр РЕ к прямой
, провести перпендикуляр РЕ к прямой  (рис. 90), то получим перпендикуляр, восстановленный (восставленный) к прямой
(рис. 90), то получим перпендикуляр, восстановленный (восставленный) к прямой  .
.
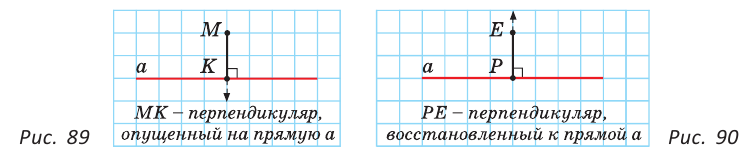
Теорема. Через точку, лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и только одну.
Дано: прямая  ; точка А;
; точка А;  (рис. 91).
(рис. 91).
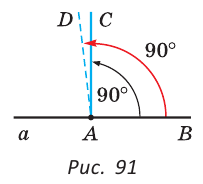
Доказать: через точку А можно провести прямую, перпендикулярную прямой  , и только одну.
, и только одну.
Доказательство:
По аксиоме откладывания углов от луча АВ в данную полуплоскость можно отложить угол CAB, равный 90°, и притом только один. Тогда прямая АС перпендикулярна прямой  . Предположим, что существует другая прямая AD, проходящая через точку А и перпендикулярная прямой
. Предположим, что существует другая прямая AD, проходящая через точку А и перпендикулярная прямой  . Тогда
. Тогда 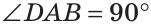 и от луча АВ в данную полуплоскость будут отложены два угла, равные 90°:
и от луча АВ в данную полуплоскость будут отложены два угла, равные 90°: 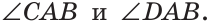 А это невозможно по аксиоме откладывания углов. Следовательно, не существует другой прямой, проходящей через точку А и перпендикулярной прямой
А это невозможно по аксиоме откладывания углов. Следовательно, не существует другой прямой, проходящей через точку А и перпендикулярной прямой  .
.
Теорема. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и притом только одну.
Дано: прямая  ; точка A,
; точка A,  (рис. 92).
(рис. 92).
Доказать: через точку А можно провести прямую, перпендикулярную прямой  , и притом только одну.
, и притом только одну.
Доказательство:
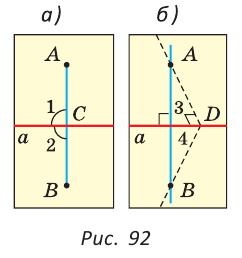
1) В начале докажем, что через точку А можно провести прямую, перпендикулярную прямой  . Мысленно перегнем лист с чертежом по прямой
. Мысленно перегнем лист с чертежом по прямой  (совместим верхнюю полуплоскость с нижней, повернув ее вокруг прямой
(совместим верхнюю полуплоскость с нижней, повернув ее вокруг прямой  ) (рис. 92, а). Точка А займет некоторое положение, которое обозначим точкой В. Вернем полуплоскости в прежнее положение и проведем прямую АВ. Так как углы 1 и 2 совпадают при наложении полуплоскостей, то они равны. А поскольку эти углы смежные, то каждый из них равен 90° и
) (рис. 92, а). Точка А займет некоторое положение, которое обозначим точкой В. Вернем полуплоскости в прежнее положение и проведем прямую АВ. Так как углы 1 и 2 совпадают при наложении полуплоскостей, то они равны. А поскольку эти углы смежные, то каждый из них равен 90° и 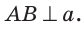
2) Теперь докажем, что АВ — единственная прямая, проходящая через точку А и перпендикулярная прямой  . Пусть прямая AD также перпендикулярна прямой
. Пусть прямая AD также перпендикулярна прямой  . Тогда
. Тогда 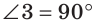 (рис. 92,6). Совместим полуплоскости еще раз. Угол 3 совпадет с углом 4, значит
(рис. 92,6). Совместим полуплоскости еще раз. Угол 3 совпадет с углом 4, значит 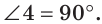 Тогда
Тогда 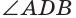 — развернутый, и через точки А и В будут проходить две прямые: ранее проведенная прямая и прямая, проходящая через точки A, D и В. А это невозможно по аксиоме прямой. Следовательно, прямая AD не перпендикулярна прямой
— развернутый, и через точки А и В будут проходить две прямые: ранее проведенная прямая и прямая, проходящая через точки A, D и В. А это невозможно по аксиоме прямой. Следовательно, прямая AD не перпендикулярна прямой  . Теорема доказана.
. Теорема доказана.
Из двух последних теорем следует, что на плоскости через любую точку можно провести прямую, перпендикулярную данной прямой, и притом только одну.
Теорема (о двух прямых, перпендикулярных третьей). На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Дано: 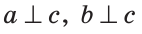 (рис. 93).
(рис. 93).
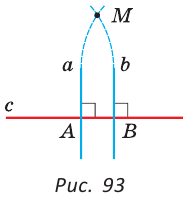
Доказать: 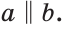
Доказательство:
Если предположить, что прямые 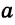 и
и 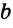 пересекаются в некоторой точке М, то окажется, что через точку М проходят две прямые
пересекаются в некоторой точке М, то окажется, что через точку М проходят две прямые 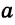 и
и 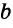 , перпендикулярные третьей прямой
, перпендикулярные третьей прямой 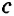 , а это невозможно. Значит, прямые
, а это невозможно. Значит, прямые 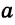 и
и 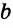 лежат в одной плоскости и не пересекаются, то есть параллельны между собой. Теорема доказана.
лежат в одной плоскости и не пересекаются, то есть параллельны между собой. Теорема доказана.
Теорема, обратная данной
Формулировка теоремы, как правило, состоит из двух частей: того, что дано, и того, что нужно доказать. Первая часть называется условием теоремы, вторая — заключением. Часто теорему формулируют в форме: «Если ...(условие теоремы), то ...(заключение теоремы)». Например, теорему о свойстве смежных углов можно сформулировать так: «Если углы смежные, то сумма этих двух углов равна 180°». «Углы смежные» — это условие теоремы, «сумма этих двух углов равна 180°» — заключение.
Если поменять условие и заключение теоремы местами, то получим утверждение, обратное данному. Для указанной выше теоремы получаем: «Если сумма двух углов равна 180°, то эти углы смежные». Но это утверждение неверно, поскольку можно привести пример двух углов, например, равных 60° и 120°, сумма которых 180°, но которые не являются смежными. Значит, приведенное утверждение не является теоремой.
Если же верно и обратное утверждение, то оно называется теоремой, обратной данной. Например, известна теорема: «Если сумма цифр числа делится на 3, то и число делится на 3» — и ей обратная: «Если число делится на 3, то и сумма цифр числа делится на 3».
Иногда прямую и обратную теоремы объединяют, употребляя при этом выражение «тогда и только тогда». Объединим вышеуказанные теоремы: «Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3».
Геометрия 3D
Пусть в пространстве прямая 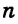 пересекает плоскость
пересекает плоскость 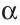 в точке В (рис. 98). Если прямая
в точке В (рис. 98). Если прямая 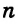 перпендикулярна любой прямой плоскости, проходящей через точку В, то она называется прямой, перпендикулярной плоскости. Пишут
перпендикулярна любой прямой плоскости, проходящей через точку В, то она называется прямой, перпендикулярной плоскости. Пишут 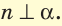 Отрезок АВ называется перпендикуляром к плоскости
Отрезок АВ называется перпендикуляром к плоскости 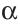 .
.
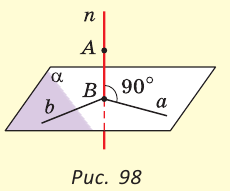
Чтобы прямая 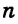 была перпендикулярна плоскости
была перпендикулярна плоскости 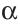 , достаточно, чтобы она была перпендикулярна каким-то двум прямым плоскости, проходящим через точку В. Например, прямым
, достаточно, чтобы она была перпендикулярна каким-то двум прямым плоскости, проходящим через точку В. Например, прямым 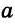 и
и 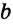 .
.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии
- Угол - определение, виды, как обозначают с примерами