
Перпендикулярность прямой и плоскости - определение и вычисление с примерами решения
Содержание:
Перпендикулярность прямой и плоскости:
Определение. Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости.
Если прямая а перпендикулярна плоскости 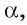
Представление о части прямой, перпендикулярной плоскости, дает прямая пересечения поверхностей стен комнаты по отношению к плоскости пола. Колонны здания расположены перпендикулярно по отношению к плоскости фундамента.
В дальнейшем понадобится следующая теорема о перпендикулярности двух параллельных прямых третьей прямой.
Теорема 1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой.
Доказательство:
Пусть а и b — параллельные прямые и 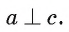 Докажем, что
Докажем, что 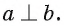 Возьмем точку О на прямой b и через нее проведем прямую
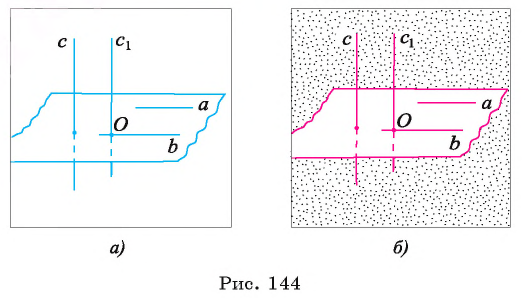
Возьмем точку О на прямой b и через нее проведем прямую 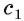 , параллельную прямой с. Тогда угол между прямыми b и с равен углу между пересекающимися прямыми b и
, параллельную прямой с. Тогда угол между прямыми b и с равен углу между пересекающимися прямыми b и 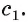 Так как
Так как 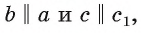 то угол между прямыми б и
то угол между прямыми б и 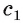 равен углу между прямыми а и с, т. е. равен
равен углу между прямыми а и с, т. е. равен 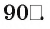 Отсюда следует, что
Отсюда следует, что 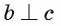 (рис. 144, а, б).
(рис. 144, а, б).
Теорема доказана.
Теперь докажем две теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью плоскости.
Теорема 2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
Доказательство:
Пусть прямые а и 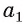 параллельны и прямая а перпендикулярна плоскости
параллельны и прямая а перпендикулярна плоскости 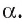 Докажем, что прямая
Докажем, что прямая 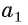 также перпендикулярна плоскости
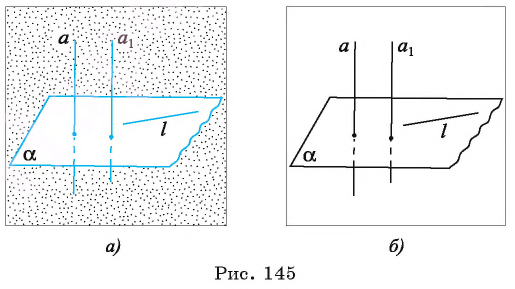
также перпендикулярна плоскости 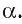 Рассмотрим произвольную прямую
Рассмотрим произвольную прямую 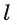 в плоскости
в плоскости 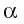 (рис. 145, а., б). Так как
(рис. 145, а., б). Так как 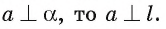 Из теоремы 1 следует, что
Из теоремы 1 следует, что 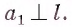 Таким образом, прямая
Таким образом, прямая 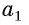 перпендикулярна любой прямой, лежащей в плоскости
перпендикулярна любой прямой, лежащей в плоскости 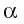 , т. е.
, т. е. 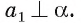
Теорема доказана.
Теорема 3 (о параллельности прямых, перпендикулярных плоскости). Если две прямые перпендикулярны одной плоскости, то они параллельны.
Доказательство:
Пусть прямые а и b перпендикулярны плоскости 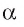 (рис. 146, а). Докажем, что прямые а и b параллельны. Допустим, что прямая b не параллельна прямой а. Через произвольную точку О прямой b проведем прямую
(рис. 146, а). Докажем, что прямые а и b параллельны. Допустим, что прямая b не параллельна прямой а. Через произвольную точку О прямой b проведем прямую 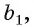 параллельную прямой а. По теореме 2 прямая
параллельную прямой а. По теореме 2 прямая 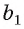 перпендикулярна плоскости а. Рассмотрим плоскость
перпендикулярна плоскости а. Рассмотрим плоскость 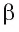 , в которой лежат прямые b и
, в которой лежат прямые b и 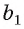 . Пусть
. Пусть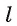 — прямая, по которой пересекаются плоскости
— прямая, по которой пересекаются плоскости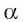 и
и 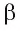 (рис. 146, б). Тогда в плоскости
(рис. 146, б). Тогда в плоскости 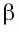 через точку О проходят две прямые b и
через точку О проходят две прямые b и 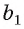 , перпендикулярные прямой I. Но это невозможно, следовательно, наше предположение неверно и
, перпендикулярные прямой I. Но это невозможно, следовательно, наше предположение неверно и 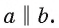
Теорема доказана.
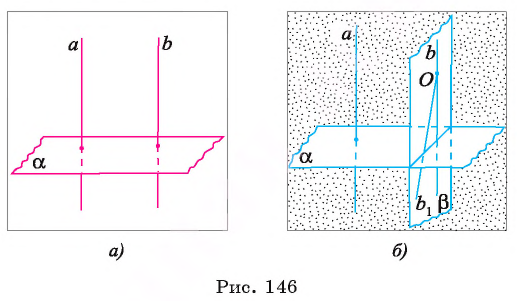
Для установления факта перпендикулярности прямой и плоскости достаточно проверить перпендикулярность прямой только двум пересекающимся прямым, лежащим в этой плоскости. Это вытекает из следующей теоремы.
Признак перпендикулярности прямой и плоскости
Теорема 4 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Доказательство:
Пусть прямая а перпендикулярна прямым р и q, лежащим в плоскости 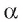 и пересекающимся в точке О. Докажем, что прямая перпендикулярна плоскости
и пересекающимся в точке О. Докажем, что прямая перпендикулярна плоскости 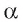 . Для этого нужно доказать, что прямая a перпендикулярна произвольной прямой
. Для этого нужно доказать, что прямая a перпендикулярна произвольной прямой 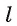 плоскости
плоскости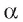 .
.
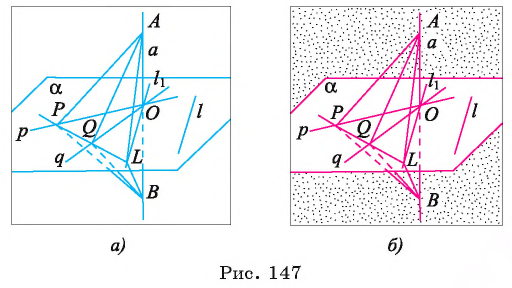
Рассмотрим первый случай, когда прямая а проходит через точку О. Проведем через точку О прямую 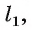 параллельную прямой
параллельную прямой 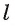 (если прямая
(если прямая 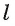 проходит через точку О, то в качестве
проходит через точку О, то в качестве 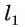 , возьмем прямую
, возьмем прямую 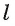 ). Отметим на прямой а точки А и В так, чтобы точка О была серединой отрезка АВ, и проведем в плоскости а прямую, пересекающую прямые р, q и I соответственно в точках Р, Q и L. Пусть для определенности точка Q лежит между точками Р и L (рис. 147, а, б).
). Отметим на прямой а точки А и В так, чтобы точка О была серединой отрезка АВ, и проведем в плоскости а прямую, пересекающую прямые р, q и I соответственно в точках Р, Q и L. Пусть для определенности точка Q лежит между точками Р и L (рис. 147, а, б).
Заметим, что 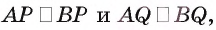 так как
так как  и
и  (указанные треугольники равны по двум катетам). Следовательно,
(указанные треугольники равны по двум катетам). Следовательно,  (так как
(так как 
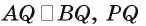 — общая сторона). Из равенства этих треугольников следует, что
— общая сторона). Из равенства этих треугольников следует, что
Треугольники APL и BPL равны (так как 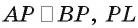 — общая сторона, a
— общая сторона, a  ), следовательно,
), следовательно,  Таким образом, треугольник ABL — равнобедренный, и его медиана OL является высотой, т. е. прямая
Таким образом, треугольник ABL — равнобедренный, и его медиана OL является высотой, т. е. прямая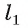 перпендикулярна прямой а. Так как прямая
перпендикулярна прямой а. Так как прямая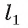 параллельна прямой
параллельна прямой 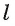 то по теореме 1
то по теореме 1 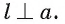 Прямая а перпендикулярна каждой прямой
Прямая а перпендикулярна каждой прямой 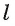 плоскости
плоскости 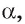 значит,
значит, 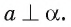
Если прямая а не проходит через точку О, тогда проведем через точку О прямую 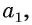 параллельную прямой а. Тогда по теореме 1
параллельную прямой а. Тогда по теореме 1 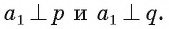 Следовательно, по доказанному в первом случае
Следовательно, по доказанному в первом случае 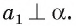 Теперь по теореме 2 прямая а перпендикулярна плоскости
Теперь по теореме 2 прямая а перпендикулярна плоскости 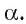 Теорема доказана.
Теорема доказана.
Теорема 5 (о плоскости, проходящей через данную точку и перпендикулярной данной прямой). Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.
Доказательство:
I. Докажем существование плоскости.
Пусть а — данная прямая, а точка О — произвольная точка пространства. Докажем, что существует плоскость, проходящая через точку О и перпендикулярная прямой а.
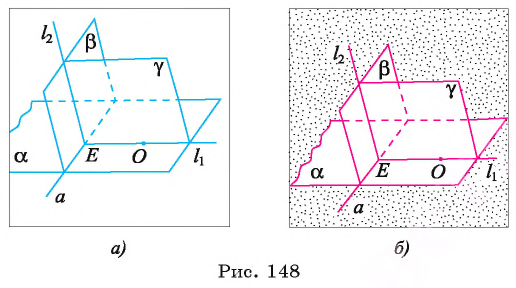
1)Рассмотрим плоскость 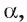 проходящую через прямую а и точку О, и плоскость
проходящую через прямую а и точку О, и плоскость 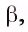 проходящую через прямую а (рис. 148, а, б).
проходящую через прямую а (рис. 148, а, б).
2)В плоскости а через точку О проведем прямую 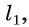 перпендикулярную прямой а. Пусть точка Е — точка пересечения прямых а и
перпендикулярную прямой а. Пусть точка Е — точка пересечения прямых а и 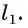
3)Через точку Е в плоскости 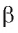 проведем прямую
проведем прямую 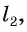 перпендикулярную прямой а.
перпендикулярную прямой а.
4)Плоскость 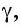 проходящая через прямые
проходящая через прямые 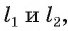 является искомой. Действительно, прямая а перпендикулярна двум пересекающимся прямым
является искомой. Действительно, прямая а перпендикулярна двум пересекающимся прямым 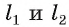 плоскости у, следовательно, она перпендикулярна плоскости
плоскости у, следовательно, она перпендикулярна плоскости 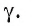
II. Докажем единственность плоскости.
Допустим, что через точку О проходит еще одна плоскость 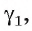 перпендикулярная прямой а. Пусть плоскость
перпендикулярная прямой а. Пусть плоскость 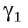 пересекает плоскость а по прямой
пересекает плоскость а по прямой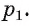 Тогда
Тогда 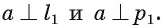 Следовательно, в плоскости
Следовательно, в плоскости 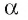 через точку О проходят две прямые
через точку О проходят две прямые 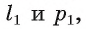 перпендикулярные прямой а. Как известно из планиметрии, этого быть не может. Таким образом, наше предположение неверно и плоскость
перпендикулярные прямой а. Как известно из планиметрии, этого быть не может. Таким образом, наше предположение неверно и плоскость 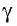 единственная.
единственная.
Теорема доказана.
Теорема 6 (о прямой, проходящей через данную точку и перпендикулярной данной плоскости). Через любую точку пространства проходит единственная прямая, перпендикулярная данной плоскости.
Доказательство:
I.Докажем существование прямой.
Пусть дана плоскость а и точка О — произвольная точка пространства. Докажем, что существует прямая, проходящая через точку О и перпендикулярная плоскости 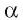 (рис. 149, а, б).
(рис. 149, а, б).
1)Проведем в плоскости 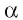 некоторую прямую а и рассмотрим плоскость
некоторую прямую а и рассмотрим плоскость 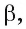 проходящую через точку О и перпендикулярную прямой а.
проходящую через точку О и перпендикулярную прямой а.
2)Обозначим буквой b прямую, по которой пересекаются плоскости 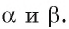
3)В плоскости 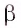 через точку О проведем прямую
через точку О проведем прямую 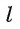 , перпендикулярную прямой b. Прямая
, перпендикулярную прямой b. Прямая 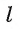 — искомая прямая. Действительно, прямая
— искомая прямая. Действительно, прямая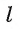 перпендикулярна двум пересекающимся прямым а и b плоскости a (
перпендикулярна двум пересекающимся прямым а и b плоскости a (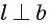 по построению и
по построению и 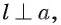 так как
так как 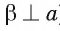 ), следовательно, она перпендикулярна плоскости а (см. рис. 149, а, б).
), следовательно, она перпендикулярна плоскости а (см. рис. 149, а, б).
II.Докажем единственность плоскости.
Предположим, что через точку О проходит еще одна прямая 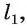 перпендикулярная плоскости
перпендикулярная плоскости 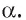 Тогда по теореме 3 прямые
Тогда по теореме 3 прямые 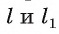 параллельны, что невозможно, так как прямые
параллельны, что невозможно, так как прямые 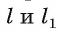 пересекаются в точке О. Таким образом, наше предположение неверно и через точку О проходит одна прямая, перпендикулярная плоскости
пересекаются в точке О. Таким образом, наше предположение неверно и через точку О проходит одна прямая, перпендикулярная плоскости 
Теорема доказана.
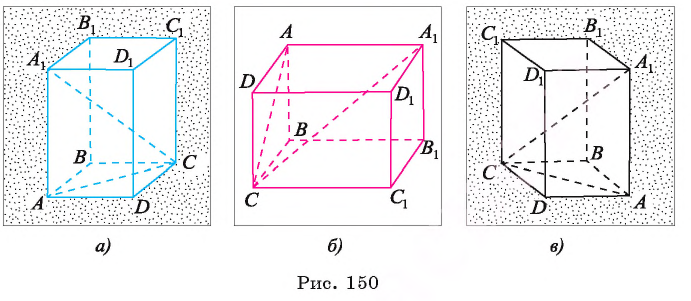
Теорема 7 (о свойстве диагонали прямоугольного параллелепипеда). Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину.
Доказательство:
Пусть 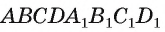 — прямоугольный параллелепипед (все его грани прямоугольники). Докажем, что
— прямоугольный параллелепипед (все его грани прямоугольники). Докажем, что 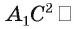
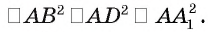
Из условия следует, что 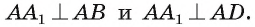 Значит, по признаку перпендикулярности прямой плоскости прямая
Значит, по признаку перпендикулярности прямой плоскости прямая 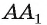 перпендикулярна плоскости, в которой лежит грань ABCD. Отсюда следует, что
перпендикулярна плоскости, в которой лежит грань ABCD. Отсюда следует, что 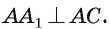 В прямоугольном треугольнике
В прямоугольном треугольнике 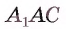 по теореме Пифагора
по теореме Пифагора 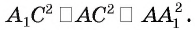 Кроме того,
Кроме того, 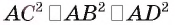 (так как АС — диагональ прямоугольника ABCD). Следовательно,
(так как АС — диагональ прямоугольника ABCD). Следовательно, 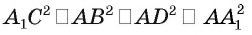 (рис. 150, а, б, в).
(рис. 150, а, б, в).
Следствие. Диагонали прямоугольного параллелепипеда равны.
Пример:
Докажите, что если прямая перпендикулярна одной из двух параллельных плоскостей, то эта прямая перпендикулярна и другой плоскости.
Доказательство:
Пусть плоскости 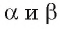 параллельны, а прямая
параллельны, а прямая 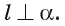 Докажем, что
Докажем, что 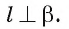
- Рассмотрим пересекающиеся прямые а и b в плоскости
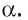
- Через произвольную точку в плоскости
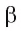 проведем прямые
проведем прямые 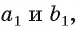 параллельные прямым а и b соответственно. Эти прямые лежат в плоскости
параллельные прямым а и b соответственно. Эти прямые лежат в плоскости 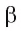 .
. - Прямая
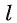 перпендикулярна прямым а и b (так как
перпендикулярна прямым а и b (так как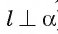 ), следовательно, она перпендикулярна прямым
), следовательно, она перпендикулярна прямым 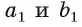 (глава 3, § 1, теорема 1).
(глава 3, § 1, теорема 1). - Таким образом, прямая
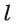 перпендикулярна двум пересекающимся прямым
перпендикулярна двум пересекающимся прямым 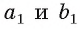 плоскости
плоскости 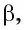 следовательно, прямая
следовательно, прямая 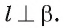
Перпендикуляр и наклонная
Пусть точка А не лежит на плоскости 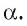 Проведем через точку А прямую, перпендикулярную плоскости
Проведем через точку А прямую, перпендикулярную плоскости 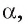 и обозначим буквой О точку пересечения этой прямой с плоскостью
и обозначим буквой О точку пересечения этой прямой с плоскостью 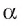 (рис. 163, а). Перпендикуляром., проведенным из точки А к плоскости
(рис. 163, а). Перпендикуляром., проведенным из точки А к плоскости 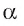 , называется отрезок АО, точка О называется основанием перпендикуляра. Если АО — перпендикуляр к плоскости
, называется отрезок АО, точка О называется основанием перпендикуляра. Если АО — перпендикуляр к плоскости 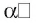 а М — произвольная точка этой плоскости, отличная от точки О, то отрезок AM называется наклонной, проведенной из точки А к плоскости
а М — произвольная точка этой плоскости, отличная от точки О, то отрезок AM называется наклонной, проведенной из точки А к плоскости 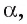 а точка М — основанием, наклонной. Отрезок ОМ — ортогональная проекция (или, короче, проекция) наклонной AM на плоскость
а точка М — основанием, наклонной. Отрезок ОМ — ортогональная проекция (или, короче, проекция) наклонной AM на плоскость 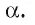
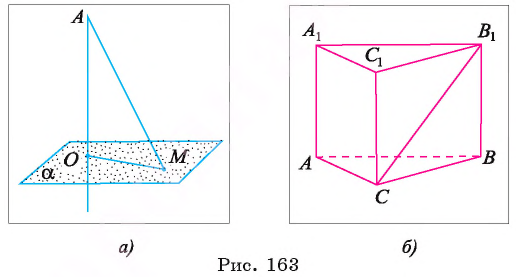
Например, если 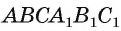 — прямая треугольная призма, то перпендикуляр, проведенный из точки
— прямая треугольная призма, то перпендикуляр, проведенный из точки 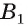 к плоскости ее основания АВС, есть ребро
к плоскости ее основания АВС, есть ребро 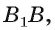 отрезок СB — проекция наклонной
отрезок СB — проекция наклонной 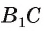 на плоскость АБС (рис. 163, б).
на плоскость АБС (рис. 163, б).
Теорема о трех перпендикулярах
Докажем теорему, которая играет важную роль при решении многих задач.
Теорема 1 (о трех перпендикулярах). Прямая, проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной.
Доказательство:
Пусть АО и AM — соответственно перпендикуляр и наклонная к плоскости 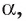 а — прямая, проведенная в плоскости
а — прямая, проведенная в плоскости 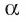 и перпендикулярная проекции ОМ (рис. 164, а, б). Докажем, что
и перпендикулярная проекции ОМ (рис. 164, а, б). Докажем, что 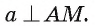
Прямая а перпендикулярна плоскости ОАМ, так как она перпендикулярна двум пересекающимся прямым OA и ОМ этой плоскости (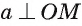 по условию,
по условию, 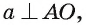 так как
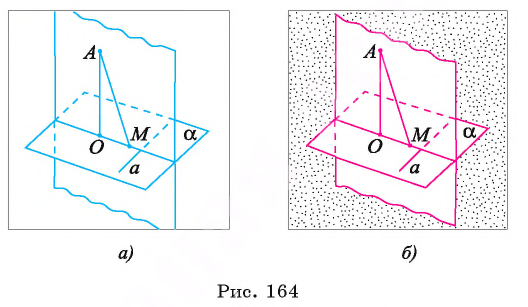
так как 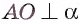 ). Следовательно, прямая а перпендикулярна любой прямой, лежащей в плоскости АОМ, т. е.
). Следовательно, прямая а перпендикулярна любой прямой, лежащей в плоскости АОМ, т. е. 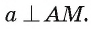
Теорема доказана.
Теорема 2. Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость.
Доказательство:
Пусть АО и AM — соответственно перпендикуляр и наклонная, проведенные из точки А к плоскости 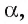 прямая а лежит в плоскости а и перпендикулярна наклонной AM (см. рис. 164, а, б). Докажем, что прямая а перпендикулярна проекции ОМ. Прямая а перпендикулярна плоскости ОАМ, так как она перпендикулярна двум пересекающимся прямым OA и AM этой плоскости (
прямая а лежит в плоскости а и перпендикулярна наклонной AM (см. рис. 164, а, б). Докажем, что прямая а перпендикулярна проекции ОМ. Прямая а перпендикулярна плоскости ОАМ, так как она перпендикулярна двум пересекающимся прямым OA и AM этой плоскости (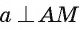 по условию,
по условию, 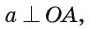 так как
так как 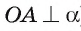 ). Отсюда следует, что прямая а перпендикулярна каждой прямой, лежащей в плоскости АОМ, в частности
). Отсюда следует, что прямая а перпендикулярна каждой прямой, лежащей в плоскости АОМ, в частности 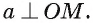
Теорема доказана.
Пример №1
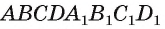 — куб, точка О — точка пересечения диагоналей грани
— куб, точка О — точка пересечения диагоналей грани 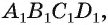 a F — середина ребра
a F — середина ребра 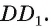 Докажите, что
Докажите, что 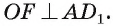
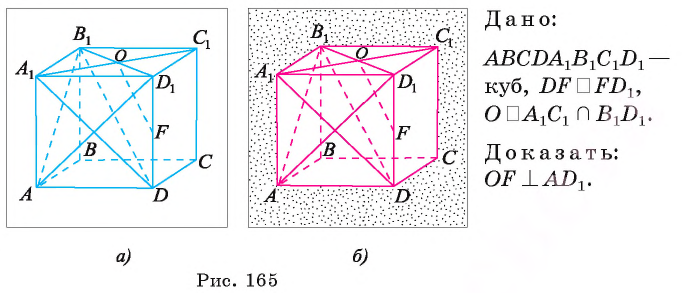
Доказательство:
1)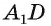 — проекция
— проекция 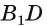 на плоскость
на плоскость 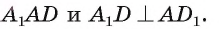 Следовательно, по теореме о трех перпендикулярах
Следовательно, по теореме о трех перпендикулярах 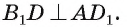
2)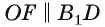 (так как OF — средняя линия треугольника
(так как OF — средняя линия треугольника 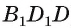 ), значит,
), значит, 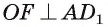 (рис. 165, а, б).
(рис. 165, а, б).
Теорема 3. Если из одной точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и две наклонные, то:
1)две наклонные, имеющие равные проекции, равны;
2)из двух наклонных больше та, проекция которой больше.
Доказательство:
Пусть АО — перпендикуляр к плоскости 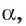 АВ и АС — наклонные к этой плоскости (рис. 166, о). По условию
АВ и АС — наклонные к этой плоскости (рис. 166, о). По условию 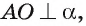 следовательно,
следовательно, 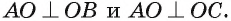 Из прямоугольных треугольников АОВ и АОС найдем
Из прямоугольных треугольников АОВ и АОС найдем 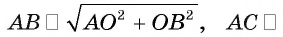
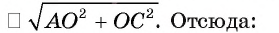
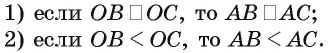
Теорема доказана.
Пусть АО и AM — соответственно перпендикуляр и наклонная, проведенные из точки А к плоскости 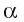 (см. рис. 166, а). В прямоугольном треугольнике АОМ сторона АО является катетом, а сторона AM — гипотенузой, следовательно,
(см. рис. 166, а). В прямоугольном треугольнике АОМ сторона АО является катетом, а сторона AM — гипотенузой, следовательно, 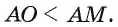 Таким образом, перпендикуляр, проведенный из точки к плоскости, меньше любой наклонной, проведенной из той же точки к данной плоскости .
Таким образом, перпендикуляр, проведенный из точки к плоскости, меньше любой наклонной, проведенной из той же точки к данной плоскости .
Значит, из всех расстояний от точки А до различных точек плоскости 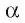 наименьшим является расстояние до основания О перпендикуляра, проведенного из точки А к плоскости
наименьшим является расстояние до основания О перпендикуляра, проведенного из точки А к плоскости 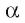 .
.
Определение. Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к данной плоскости.
Расстояние от точки А до прямой 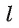 обозначается d (А,
обозначается d (А, 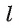 ) (читают: «Расстояние от точки А до прямой
) (читают: «Расстояние от точки А до прямой 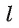 »).
»).
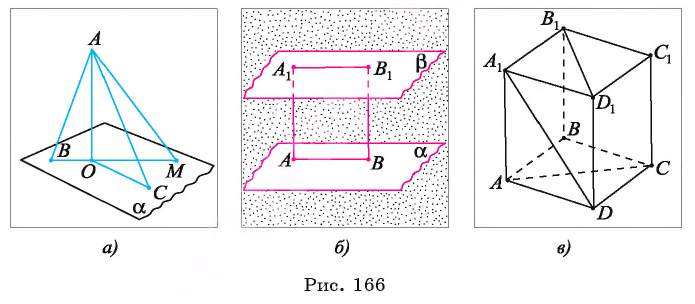
Пусть 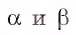 — параллельные плоскости. Из любых точек А и Б плоскости
— параллельные плоскости. Из любых точек А и Б плоскости 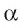 проведем к плоскости
проведем к плоскости 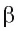 перпендикуляры
перпендикуляры 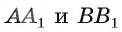 (рис. 166, б). Так как
(рис. 166, б). Так как 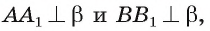 то
то 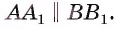 Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны, следовательно,
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны, следовательно, 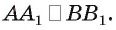 Отсюда следует, что все точки плоскости а находятся на одном и том же расстоянии от плоскости
Отсюда следует, что все точки плоскости а находятся на одном и том же расстоянии от плоскости 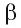 . Аналогично, все точки плоскости
. Аналогично, все точки плоскости 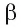 находятся на том же расстоянии от плоскости
находятся на том же расстоянии от плоскости 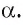
Определение. Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.
Расстояние между параллельными плоскостями 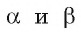 обозначается d
обозначается d 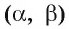 (читают: «Расстояние между плоскостями
(читают: «Расстояние между плоскостями 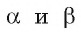 »).
»).
Аналогично, каждая точка прямой, параллельной некоторой плоскости, находится на одном и том же расстоянии от этой плоскости.
Определение. Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до плоскости.
Расстояние между прямой 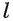 и параллельной ей плоскостью а обозначается d (
и параллельной ей плоскостью а обозначается d (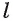 ,
, 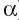 ) (читают: «Расстояние между прямой
) (читают: «Расстояние между прямой 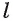 и плоскостью
и плоскостью 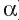 »).
»).
Если две прямые скрещивающиеся, то через каждую из них проходит единственная плоскость, параллельная другой.
Определение. Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой.
Расстояние между скрещивающимися прямыми а и b обозначается d (а, b) (читают: « Расстояние между прямыми а и b »).
Например, в прямоугольном параллелепипеде 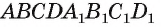 расстояние между параллельными плоскостями, в которых лежат грани
расстояние между параллельными плоскостями, в которых лежат грани 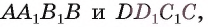 равно длине ребра AD, так как AD перпендикулярно каждой из указанных плоскостей. Расстояние от прямой
равно длине ребра AD, так как AD перпендикулярно каждой из указанных плоскостей. Расстояние от прямой 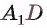 до параллельной ей плоскости
до параллельной ей плоскости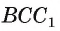 равно длине ребра DC (рис. 166, в).
равно длине ребра DC (рис. 166, в).
Пример №2
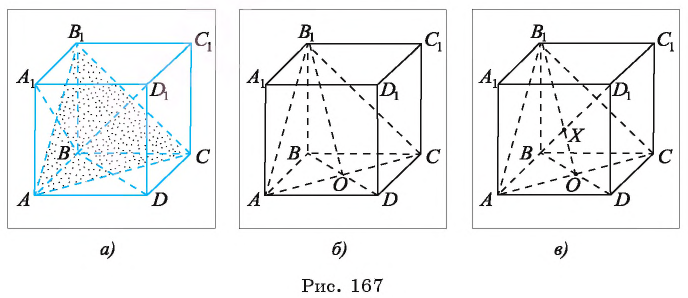
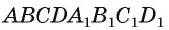 — куб. Постройте основание перпендикуляра, проведенного из точки
— куб. Постройте основание перпендикуляра, проведенного из точки 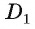 к плоскости
к плоскости 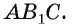
Решение:
1)Заметим, что 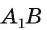 — проекция
— проекция 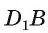 на плоскость грани
на плоскость грани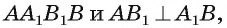 следовательно, по теореме о трех перпендикулярах
следовательно, по теореме о трех перпендикулярах 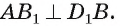 Аналогично, DB — проекция
Аналогично, DB — проекция 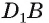 на плоскость грани AJBCD и
на плоскость грани AJBCD и 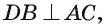 значит,
значит, 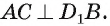 Таким образом, прямая В,В перпендикулярна двум пересекающимся прямым
Таким образом, прямая В,В перпендикулярна двум пересекающимся прямым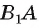 и АС плоскости
и АС плоскости 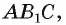 следовательно, прямая
следовательно, прямая 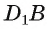 перпендикулярна плоскости
перпендикулярна плоскости 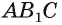 (рис. 167, а).
(рис. 167, а).
2)Так как 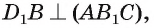 то искомое основание перпендикуляра есть точка пересечения прямой
то искомое основание перпендикуляра есть точка пересечения прямой 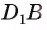 с плоскостью
с плоскостью 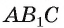 (см. рис. 167, а).
(см. рис. 167, а).
3)Строим точку 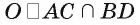 (рис. 167, б).
(рис. 167, б).
4)Точка 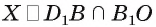 — искомое основание перпендикуляра (точка X лежит в плоскости
— искомое основание перпендикуляра (точка X лежит в плоскости 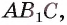 так как она лежит на прямой
так как она лежит на прямой 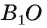 (рис. 167, в)).
(рис. 167, в)).
Пример №3
Дан куб 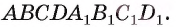 Найдите расстояние между прямыми
Найдите расстояние между прямыми 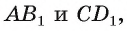 если длина ребра куба равна а.
если длина ребра куба равна а.
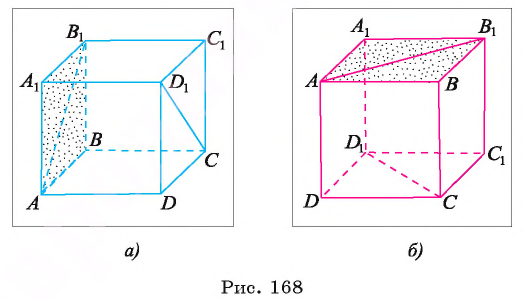
Решение:
1)Рассмотрим плоскость, проходящую через прямую 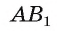 и параллельную прямой
и параллельную прямой 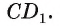 Такой плоскостью является плоскость
Такой плоскостью является плоскость 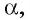 в которой лежит грань
в которой лежит грань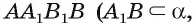
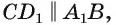 следовательно,
следовательно, 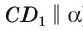 ) ( рис. 168, а, б).
) ( рис. 168, а, б).
2)Расстояние между прямыми 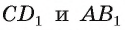 есть расстояние от любой точки прямой
есть расстояние от любой точки прямой 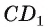 до плоскости а. Отрезок
до плоскости а. Отрезок 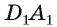 — перпендикуляр, проведенный из точки
— перпендикуляр, проведенный из точки 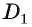 к плоскости
к плоскости  значит,
значит, 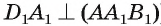 ), следовательно, его длина а равна расстоянию между прямыми
), следовательно, его длина а равна расстоянию между прямыми 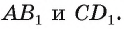 Ответ:
Ответ: 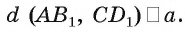
Угол между прямой и плоскостью
Ортогональная проекция прямой
Пусть в пространстве даны плоскость 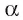 и прямая а. Ортогональной проекцией прямой а на плоскость
и прямая а. Ортогональной проекцией прямой а на плоскость 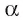 называется проекция этой прямой на плоскость а в случае, если прямая, определяющая направление проектирования, перпендикулярна плоскости
называется проекция этой прямой на плоскость а в случае, если прямая, определяющая направление проектирования, перпендикулярна плоскости 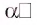 Например, если
Например, если 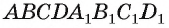 — куб, тогда ортогональной проекцией прямой
— куб, тогда ортогональной проекцией прямой 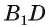 на плоскость грани
на плоскость грани 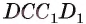 является прямая
является прямая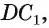 а ортогональная проекция этой прямой на плоскость основания ABCD куба есть прямая RD (рис. 171, а).
а ортогональная проекция этой прямой на плоскость основания ABCD куба есть прямая RD (рис. 171, а).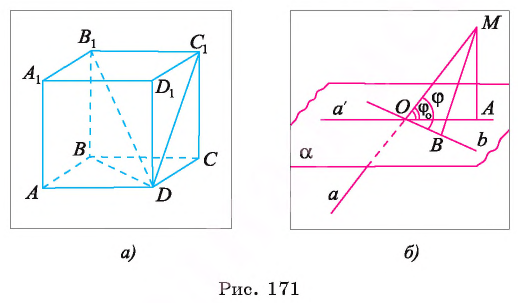
Дадим определение угла между прямой и плоскостью, при этом воспользуемся понятием ортогональной проекции прямой на плоскость.
Если прямая перпендикулярна плоскости, то ее ортогональная проекция на эту плоскость есть точка пересечения этой прямой с плоскостью. В этом случае угол между прямой и плоскостью считается равным 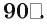
Угол между прямой и плоскостью
Рассмотрим понятие угла между прямой и плоскостью.
Определение. Углом между прямой, не перпендикулярной плоскости, и плоскостью называется угол между прямой и ее ортогональной проекцией на данную плоскость.
Теорема. Угол между прямой и плоскостью является наименьшим из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.
Доказательство:
Пусть прямая а пересекает плоскость 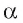 в точке О,
в точке О, 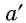 — ортогональная проекция прямой а на плоскость
— ортогональная проекция прямой а на плоскость 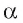 , b — произвольная прямая, лежащая в плоскости а, проходящая через точку О и не совпадающая с прямой
, b — произвольная прямая, лежащая в плоскости а, проходящая через точку О и не совпадающая с прямой 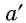 . Обозначим буквой
. Обозначим буквой 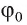 угол между прямыми а и
угол между прямыми а и 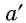 , а буквой
, а буквой 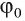 — угол между прямыми а и b. Докажем, что
— угол между прямыми а и b. Докажем, что 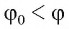 (рис. 171, б).
(рис. 171, б).
Если прямые а и b не перпендикулярны, то из точки 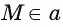 проведем перпендикуляры МА и MB к прямым
проведем перпендикуляры МА и MB к прямым 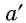 и b соответственно. Из прямоугольных треугольников МАО и МВО найдем
и b соответственно. Из прямоугольных треугольников МАО и МВО найдем  Так как МА<МВ, то
Так как МА<МВ, то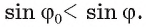 Отсюда следует, что
Отсюда следует, что 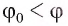 (так как
(так как 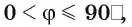 а функция
а функция 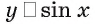 на указанном промежутке является возрастающей).
на указанном промежутке является возрастающей).
Если 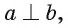 то
то  а, значит,
а, значит, 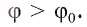
Теорема доказана.
Пример №4
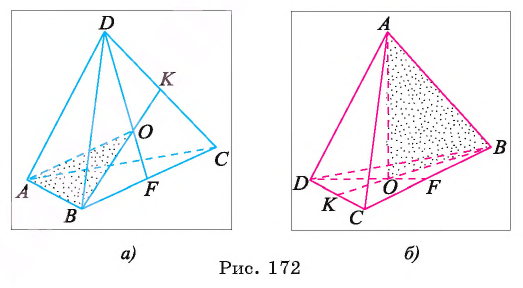
Дан тетраэдр DABC. Найдите косинус угла между прямой АВ и плоскостью ВВС.
Решение:
1) Угол между прямой АВ и плоскостью DBC равен углу между прямой АВ и ортогональной проекцией этой прямой на плоскость DBC.
2) Для построения ортогональной проекции прямой АВ на плоскость DBC достаточно построить основание перпендикуляра, проведенного из произвольной точки прямой АВ к плоскости DBC (например, из точки А).
3) Если точка О — основание перпендикуляра, проведенного из точки А к плоскости DBC, то 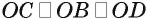 (проекции равных соответственно наклонных AC, АВ, AD). Следовательно, точка О равноудалена от вершин треугольника DBC, а такой точкой в равностороннем треугольнике DBC является точка пересечения медиан В К и DF. Таким образом, прямая ВО — перпендикулярная проекция прямой АВ на плоскость DBC (рис. 172, а, б).
(проекции равных соответственно наклонных AC, АВ, AD). Следовательно, точка О равноудалена от вершин треугольника DBC, а такой точкой в равностороннем треугольнике DBC является точка пересечения медиан В К и DF. Таким образом, прямая ВО — перпендикулярная проекция прямой АВ на плоскость DBC (рис. 172, а, б).
4) Теперь найдем косинус угла между прямой АВ и плоскостью DBC. Пусть ребро тетраэдра равно а. В прямоугольном треугольнике 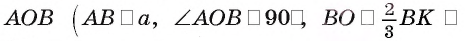
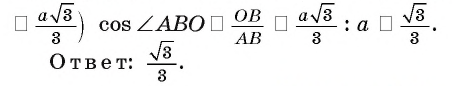
Двугранный угол
Пусть прямая а лежит в плоскости, тогда можно указать две части этой плоскости, каждая из которых вместе с прямой а называется полуплоскостью. Прямая а называется граничной для каждой из полуплоскостей (рис. 174, а). Две полуплоскости с общей граничной прямой 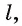 расположенные в пространстве, могут не лежать в одной плоскости (рис. 175, б).
расположенные в пространстве, могут не лежать в одной плоскости (рис. 175, б).
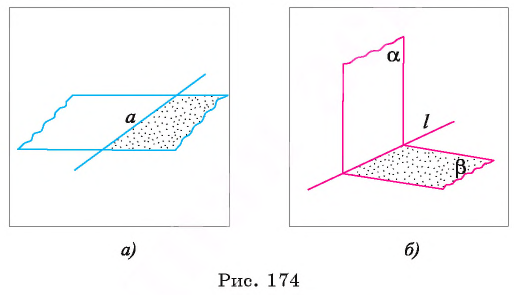
Определение. Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей.
Полуплоскости называются гранями, двугранного угла, общая граничная прямая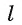 полуплоскостей называется ребром двугранного угла (см. рис. 174, б).
полуплоскостей называется ребром двугранного угла (см. рис. 174, б).
Если грани двугранного угла лежат в одной плоскости, то он называется развернутым..
Линейный угол двугранного угла
Для измерения двугранного угла вводится понятие его линейного угла. Пусть точка О лежит на ребре 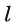 двугранного угла (рис. 175, а). В каждой грани проведем лучи OA и ОВ перпендикулярно ребру
двугранного угла (рис. 175, а). В каждой грани проведем лучи OA и ОВ перпендикулярно ребру 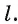 Угол АОВ, сторонами которого служат лучи OA и ОВ, называется линейным утлом данного двугранного угла.
Угол АОВ, сторонами которого служат лучи OA и ОВ, называется линейным утлом данного двугранного угла.
Определение. Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
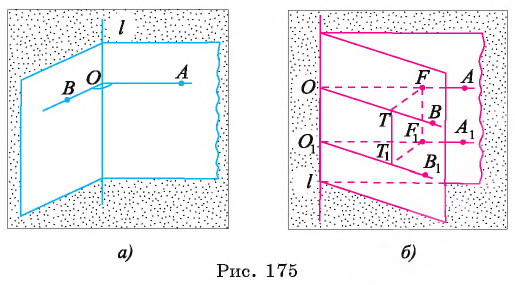
Пусть АОВ — линейный угол двугранного угла, ребро которого 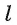 (см. рис. 175, а). Так как
(см. рис. 175, а). Так как 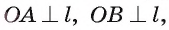 то плоскость, в которой лежат лучи OA и ОБ, перпендикулярна прямой
то плоскость, в которой лежат лучи OA и ОБ, перпендикулярна прямой 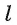 . Таким образом, линейный угол двугранного угла — это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру.
. Таким образом, линейный угол двугранного угла — это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру.
Все линейные углы двугранного угла равны между собой. Действительно, рассмотрим два линейных угла АОВ и 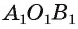 двугранного угла, ребро которого
двугранного угла, ребро которого 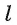 . Лучи OA и
. Лучи OA и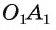 , лежат в одной грани и перпендикулярны ребру
, лежат в одной грани и перпендикулярны ребру 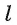 , следовательно,
, следовательно, 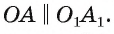 Аналогично
Аналогично 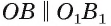 (рис. 175, б). Отложим на лучах OA и
(рис. 175, б). Отложим на лучах OA и 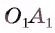 , равные отрезки OF и
, равные отрезки OF и 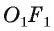 соответственно, а на лучах ОВ и
соответственно, а на лучах ОВ и 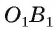 , равные отрезки ОТ и
, равные отрезки ОТ и 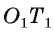 , соответственно. Так как
, соответственно. Так как 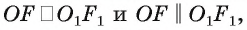 то четырехугольник
то четырехугольник 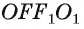 — параллелограмм. Поэтому
— параллелограмм. Поэтому 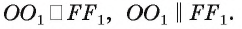 Аналогично,
Аналогично, 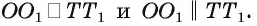 В результате
В результате  и
и 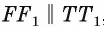 ,т. е. четырехугольник
,т. е. четырехугольник 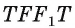 — параллелограмм. Следовательно,
— параллелограмм. Следовательно, 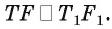 Таким образом, треугольники OFT и
Таким образом, треугольники OFT и 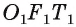 равны по трем сторонам, значит,
равны по трем сторонам, значит,  т. е.
т. е. 
Градусной мерой двугранного угла называется градусная мера его линейного угла.
Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 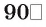 (меньше
(меньше 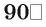 больше
больше 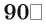 ).
).
На рисунке 176, а, б изображены соответственно острый и тупой двугранные углы.
В дальнейшем под двугранным углом будем понимать всегда тот, линейный угол 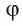 которого удовлетворяет условию
которого удовлетворяет условию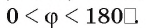
Вместо «двугранный угол, градусная мера которого равна 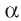 » можно говорить «двугранный угол, равный
» можно говорить «двугранный угол, равный 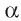 ».
».
Двугранный угол, ребро которого есть прямая АВ, а гранями являются полуплоскости 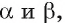 обозначается
обозначается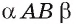 (или TABE, если на разных его гранях отмечены точки T и E).
(или TABE, если на разных его гранях отмечены точки T и E).
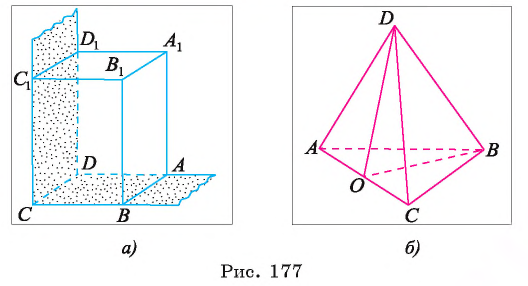
Рассмотрим примеры. Пусть 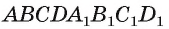 — прямоугольный параллелепипед. Тогда
— прямоугольный параллелепипед. Тогда 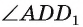 является линейным углом двугранного угла, ребро которого есть прямая DC, а его грани — полуплоскости, в которых лежат прямоугольники ABCD и
является линейным углом двугранного угла, ребро которого есть прямая DC, а его грани — полуплоскости, в которых лежат прямоугольники ABCD и 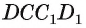 (так как
(так как 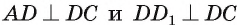 ). Угол
). Угол 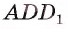 — прямой, следовательно, указанный двугранный угол прямой (рис. 177, а).
— прямой, следовательно, указанный двугранный угол прямой (рис. 177, а).
Двугранным углом при ребре многогранника называется двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по данному ребру многогранника.
Пусть DABC — правильная треугольная пирамида, а точка О — середина отрезка АС. Угол DOB есть линейный угол двугранного угла DACB, ребро которого — прямая АС, а гранями являются полуплоскости, содержащие треугольники ABC и ACD (так как 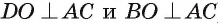 ) (рис. 177, б).
) (рис. 177, б).
Угол между плоскостями
Введем понятие угла между плоскостями.
Определение. Углом между пересекающимися плоскостями называется угол между прямыми, проведенными соответственно в плоскостях перпендикулярно их линии пересечения через некоторую ее точку.
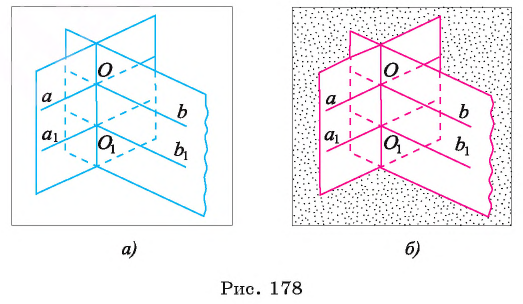
Заметим, что определение угла между плоскостями не зависит от выбора прямых а и b, проведенных в плоскостях и перпендикулярных их линии пересечения. Действительно, если в данных плоскостях провести какие-нибудь другие прямые 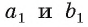 перпендикулярно их линии пересечения
перпендикулярно их линии пересечения 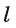 через точку
через точку 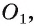 то
то 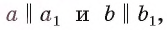 а, следовательно, угол между прямыми а и b равен углу между прямыми
а, следовательно, угол между прямыми а и b равен углу между прямыми 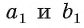 (рис. 178, а, б).
(рис. 178, а, б).
Если плоскости параллельны, то угол между ними считается равным 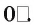 Угол между плоскостями
Угол между плоскостями 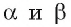 обозначается
обозначается 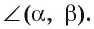 Из определения следует, что угол между пересекающимися плоскостями удовлетворяет условию
Из определения следует, что угол между пересекающимися плоскостями удовлетворяет условию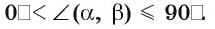
Определение. Две плоскости называются перпендикулярными, если угол между ними равен 
Теорема 1 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
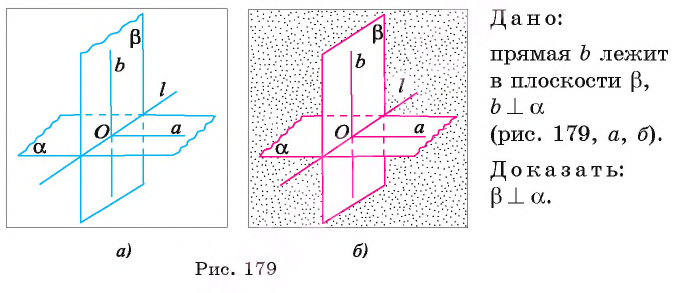
Доказательство:
1)Пусть точка О — точка пересечения прямой b с плоскостью 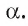 Точка О — общая точка плоскостей
Точка О — общая точка плоскостей 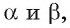 следовательно, данные плоскости пересекаются по прямой
следовательно, данные плоскости пересекаются по прямой 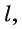 проходящей через точку О.
проходящей через точку О.
2)В плоскости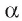 через точку О проведем прямую а, перпендикулярную прямой
через точку О проведем прямую а, перпендикулярную прямой 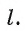
3)Прямые а и 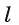 лежат в плоскости а и по условию
лежат в плоскости а и по условию 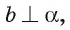 следовательно,
следовательно, 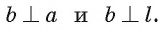 Таким образом,
Таким образом,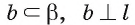
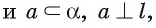 значит,
значит, 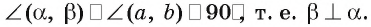
Теорема доказана.
Теорема 2. Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.
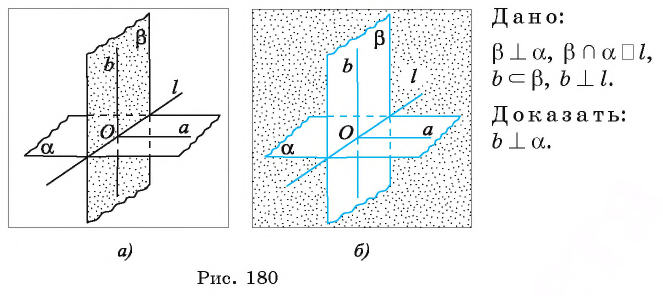
Доказательство:
- Обозначим буквой О точку пересечения прямой b с прямой
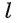 (рис. 180, а, б).
(рис. 180, а, б). - Проведем в плоскости
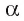 через точку О прямую а перпендикулярно прямой
через точку О прямую а перпендикулярно прямой 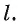
- Прямые a и b перпендикулярны прямой
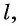 по которой пересекаются плоскости
по которой пересекаются плоскости 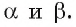 Следовательно, угол между прямыми а и b равен углу между плоскостями
Следовательно, угол между прямыми а и b равен углу между плоскостями 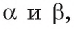 значит, равен
значит, равен 
- Таким образом, прямая b перпендикулярна пересекающимся прямым а и b плоскости
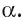 Следовательно,
Следовательно, 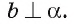
Теорема доказана.
Пример №5
Докажите, что прямая, проведенная через точку одной из перпендикулярных плоскостей и перпендикулярная другой плоскости, лежит в первой плоскости.
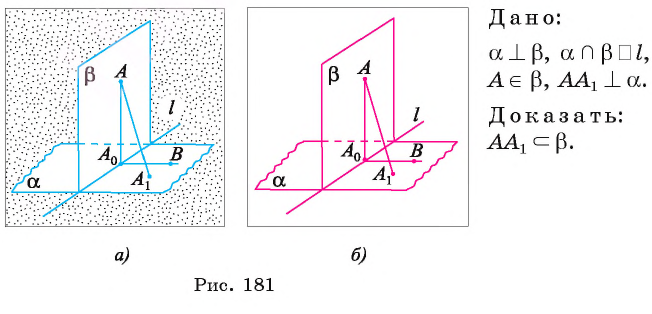
Доказательство:
Предположим, что прямая 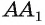 не лежит в плоскости
не лежит в плоскости 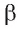 (рис. 181, а, б). Проведем в плоскости
(рис. 181, а, б). Проведем в плоскости 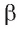 прямую
прямую 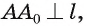 а в плоскости
а в плоскости 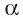 проведем
проведем 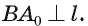 Тогда
Тогда 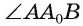 есть линейный угол двугранного угла
есть линейный угол двугранного угла 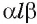 . Так как
. Так как 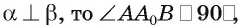 т. е.
т. е. 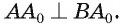 Прямая
Прямая 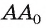 перпендикулярна двум пересекающимся прямым
перпендикулярна двум пересекающимся прямым 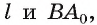 лежащим в плоскости
лежащим в плоскости 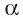 , значит,
, значит, 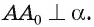 Это противоречит существованию единственной прямой, проходящей через точку и перпендикулярной плоскости. Предположение, что прямая
Это противоречит существованию единственной прямой, проходящей через точку и перпендикулярной плоскости. Предположение, что прямая 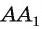 не лежит в плоскости
не лежит в плоскости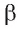 , неверное, а значит, прямая
, неверное, а значит, прямая 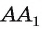 лежит в плоскости
лежит в плоскости 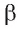 .
.
Пример №6
Основание прямой призмы 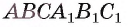 — треугольник ABC, в котором
— треугольник ABC, в котором 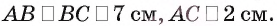 Через прямую АС проведена плоскость
Через прямую АС проведена плоскость 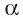 под углом
под углом  плоскости АБС, пересекающая боковое ребро
плоскости АБС, пересекающая боковое ребро 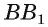 в точке D. Вычислите площадь полученного сечения (рис. 182, а, б).
в точке D. Вычислите площадь полученного сечения (рис. 182, а, б).
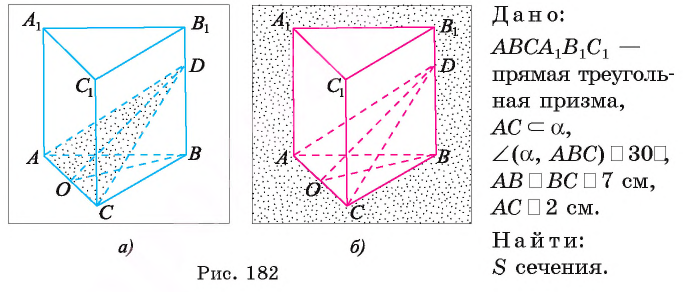
Решение:
1)В треугольнике ADC сторона 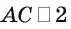 см. Для нахождения его площади необходимо найти высоту, проведенную к стороне АС (см. рис. 182, а, б).
см. Для нахождения его площади необходимо найти высоту, проведенную к стороне АС (см. рис. 182, а, б).
2)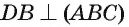 (так как призма прямая, то
(так как призма прямая, то 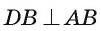 и
и 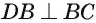 ). Кроме того,
). Кроме того,  (наклонные, имеющие равные проекции С В и АВ).
(наклонные, имеющие равные проекции С В и АВ).
3)Пусть точка О — середина отрезка АС, тогда медиана DO — высота равнобедренного треугольника 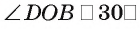 (так как
(так как 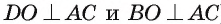 ).
).
4)В треугольнике ВОС длина катета 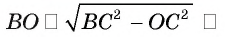
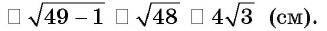
5)В треугольнике 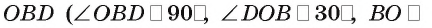
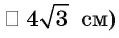 длина гипотенузы
длина гипотенузы 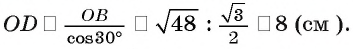
6)Теперь найдем 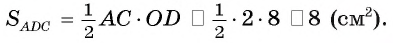
Ответ: 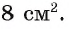
Пример №7
Докажите, что площадь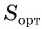 ортогональной проекции треугольника ABC на плоскость равна произведению его площади S на косинус угла
ортогональной проекции треугольника ABC на плоскость равна произведению его площади S на косинус угла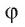 между плоскостью треугольника и плоскостью проекции:
между плоскостью треугольника и плоскостью проекции: 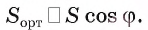
Изображение фигур
Параллельное проектирование
Для изображения на плоскости (например, на листе бумаги) геометрических фигур, расположенных в пространстве, используется параллельное проектирование. Определяется оно следующим образом.
Пусть 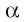 — некоторая плоскость, а
— некоторая плоскость, а 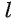 — некоторая прямая, пересекающая эту плоскость. Возьмем в пространстве произвольную точку X. Если точка X не лежит на прямой I, то проведем через точку X прямую, параллельную прямой I, и обозначим через
— некоторая прямая, пересекающая эту плоскость. Возьмем в пространстве произвольную точку X. Если точка X не лежит на прямой I, то проведем через точку X прямую, параллельную прямой I, и обозначим через 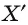 точку пересечения этой прямой с плоскостью
точку пересечения этой прямой с плоскостью 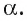 Если точка X лежит на прямой
Если точка X лежит на прямой 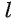 , то обозначим через
, то обозначим через 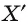 точку пересечения прямой
точку пересечения прямой 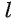 с плоскостью
с плоскостью 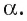
Точка X' называется проекцией точки X на плоскость 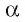 при проектировании параллельно прямой
при проектировании параллельно прямой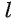 (или параллельной проекцией точки X).
(или параллельной проекцией точки X).
Плоскость 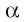 называется плоскостью проекций, а о прямой
называется плоскостью проекций, а о прямой 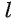 говорят, что она задает направление проецирования (рис. 188, а). Все прямые, параллельные прямой
говорят, что она задает направление проецирования (рис. 188, а). Все прямые, параллельные прямой  , задают одно и то же направление проектирования, поэтому также называются проектирующими прямыми.
, задают одно и то же направление проектирования, поэтому также называются проектирующими прямыми.
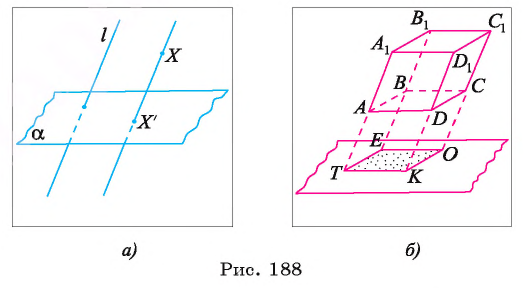
Пусть F — плоская или пространственная фигура. Проекцией фигуры, F на плоскость а при проектировании параллельно прямой 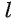 называется множество F' проекций всех точек фигуры F. Например, если плоскость а параллельна основанию ABCD параллелепипеда
называется множество F' проекций всех точек фигуры F. Например, если плоскость а параллельна основанию ABCD параллелепипеда 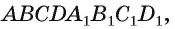 а прямая
а прямая 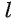 параллельна прямой
параллельна прямой 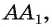 то проекцией параллелепипеда на плоскость
то проекцией параллелепипеда на плоскость 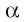 является параллелограмм ТЕОК (рис. 188, б).
является параллелограмм ТЕОК (рис. 188, б).
Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.
Сформулируем и докажем основные свойства параллельного проектирования при условии, что проектируемые отрезки и прямые не параллельны прямой, задающей направление проектирования.
Свойство 1. Проекция прямой есть прямая, а проекция отрезка — отрезок.
Доказательство:
Пусть b — некоторая прямая, не параллельная прямой 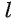 , которая задает направление проектирования. Не ограничивая общности, можем считать, что прямые b и
, которая задает направление проектирования. Не ограничивая общности, можем считать, что прямые b и 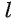 пересекаются. Через прямые b и
пересекаются. Через прямые b и 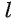 проходит единственная плоскость
проходит единственная плоскость 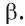 Она пересекает плоскость
Она пересекает плоскость 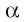 по некоторой прямой
по некоторой прямой 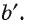 Эта прямая и является проекцией прямой b на плоскость
Эта прямая и является проекцией прямой b на плоскость 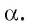 Действительно, пусть точка
Действительно, пусть точка 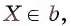 а точка
а точка 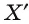 — ее проекция на плоскость
— ее проекция на плоскость 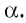 Тогда проектирующая прямая
Тогда проектирующая прямая 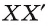 лежит в плоскости
лежит в плоскости 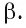 Плоскость
Плоскость 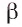 пересекает а по прямой
пересекает а по прямой 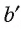 , следовательно, точка
, следовательно, точка 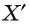 лежит на прямой
лежит на прямой 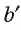 . Кроме того, каждая точка прямой
. Кроме того, каждая точка прямой 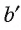 является проекцией некоторой точки прямой b. Таким образом, прямая
является проекцией некоторой точки прямой b. Таким образом, прямая 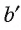 — проекция прямой b (рис. 189, а, б).
— проекция прямой b (рис. 189, а, б).
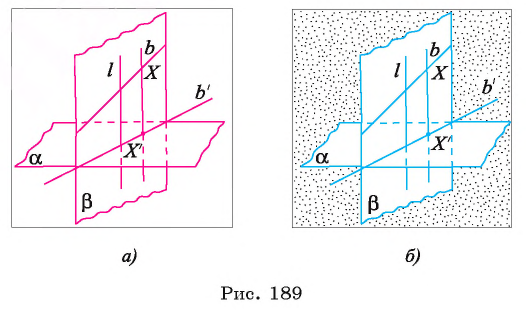
Теперь нетрудно понять, что проекция отрезка есть отрезок.
Свойство 2. Проекции параллельных прямых параллельны или совпадают.
Доказательство:
Пусть даны две параллельные прямые b и с. Возможны два случая.
1) Некоторая проектирующая прямая а пересекает обе прямые b и с. В этом случае прямая а, а также все остальные проектирующие прямые, пересекающие прямые b и с, лежат в одной плоскости 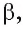 проходящей через параллельные прямые b и с. Но тогда по свойству 1 проекцией прямой b и прямой с будет прямая
проходящей через параллельные прямые b и с. Но тогда по свойству 1 проекцией прямой b и прямой с будет прямая 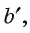 по которой пересекаются плоскости
по которой пересекаются плоскости 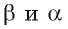 (рис. 190,а)
(рис. 190,а)
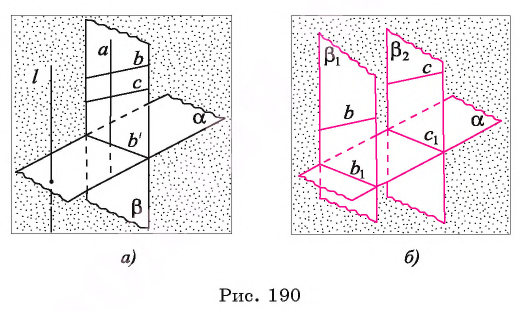
2) Не существует проектирующих прямых, пересекающих прямые b и с одновременно. Пусть 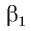 — плоскость, в которой лежат все прямые, проектирующие точки прямой b на плоскость
— плоскость, в которой лежат все прямые, проектирующие точки прямой b на плоскость 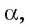 а
а 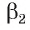 — плоскость, в которой лежат прямые, проектирующие точки прямой с на плоскость
— плоскость, в которой лежат прямые, проектирующие точки прямой с на плоскость 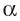 . Плоскости
. Плоскости 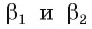 параллельны, следовательно, проекции
параллельны, следовательно, проекции 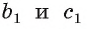 , прямых b и с параллельны как линии пересечения параллельных плоскостей
, прямых b и с параллельны как линии пересечения параллельных плоскостей 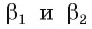 с плоскостью
с плоскостью 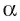 (рис. 190, б).
(рис. 190, б).
Свойство 3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.
Доказательство:
1) Пусть отрезки АВ и CD лежат на одной прямой b, а прямая 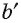 — проекция прямой b на плоскость а параллельно прямой
— проекция прямой b на плоскость а параллельно прямой 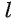 (рис. 191, а). Проекции
(рис. 191, а). Проекции 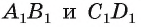 отрезков АВ и CD лежат на прямой
отрезков АВ и CD лежат на прямой 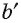 . Проектирующие прямые
. Проектирующие прямые 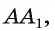
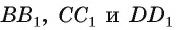 параллельны между собой и лежат в одной плоскости
параллельны между собой и лежат в одной плоскости 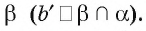 Из планиметрии известно, что параллельные прямые
Из планиметрии известно, что параллельные прямые 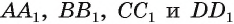 отсекают от двух прямых b и
отсекают от двух прямых b и 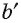 плоскости
плоскости 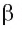 пропорциональные отрезки, т. е.
пропорциональные отрезки, т. е. 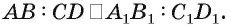
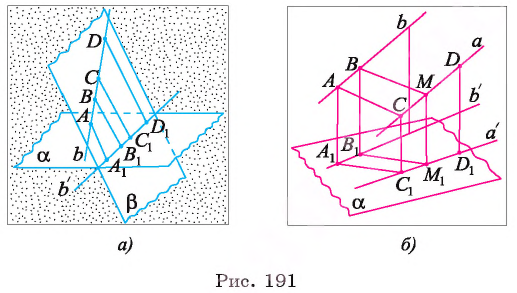
Пусть отрезки АВ и CD лежат на параллельных прямых b и а (рис. 191, б). Проведем прямую АС и через точку В, параллельную ей прямую, которая пересекает прямую а в некоторой точке М. Четырехугольник АВМС — параллелограмм. Рассмотрим случай, когда его проекция на плоскость 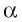 есть параллелограмм
есть параллелограмм 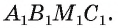 Тогда
Тогда 
 По доказанному
По доказанному 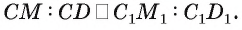 Таким образом,
Таким образом, 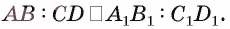
Если проекция параллелограмма АВМС есть отрезок (в случае, когда проекции прямых а и b совпадают), доказательство данного свойства еще проще.
Следствие. При параллельном проектировании середина отрезка проектируется в середину его проекции.
Изображение фигур
Рассмотренные в предыдущем параграфе свойства параллельного проектирования применяются при выполнении рисунков (изображений фигур), иллюстрирующих теоремы и задачи стереометрии.
Изображением, фигуры F называется любая фигура, подобная проекции этой фигуры на некоторую плоскость.
Выполняя изображения фигур, расположенных в пространстве, необходимо учитывать свойства, сохраняющиеся при параллельном проектировании, а в остальном изображение может быть произвольным. Важно только, чтобы изображения рассматриваемых фигур были наглядными и давали верное представление о них.
При различном выборе плоскости проекций и направления проектирования получаются различные проекции данной фигуры, а значит, и различные ее изображения. Например, изображениями куба являются фигуры, данные на рисунке 192, а, б, в, г.
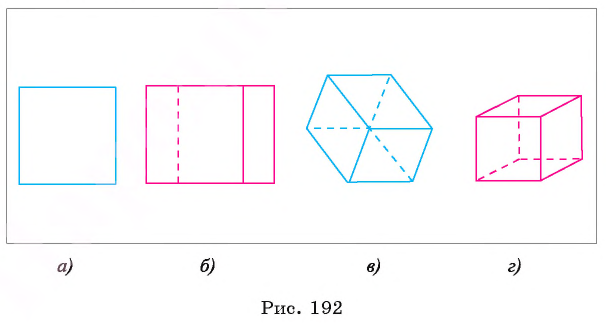
Изображение куба, данное на рисунке 192, а, не дает представления о кубе, наглядным является изображение, данное на рисунке 192, г. При построении изображений плоских фигур, расположенных в пространстве, предполагается, что плоскости рассматриваемых фигур не параллельны направлению проектирования.
1. В качестве изображения данного треугольника можно взять произвольный треугольник.
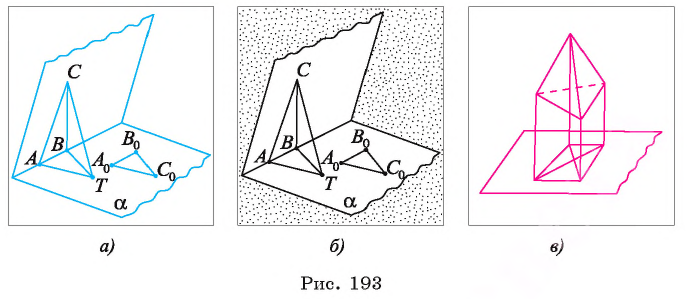
Действительно, пусть даны два треугольника ABC и 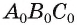 (рис. 193, а, б). Обозначим плоскость а, проходящую через прямую АВ, a АВТ — треугольник в этой плоскости, подобный треугольнику
(рис. 193, а, б). Обозначим плоскость а, проходящую через прямую АВ, a АВТ — треугольник в этой плоскости, подобный треугольнику 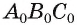 . Тогда при проектировании на плоскость а параллельно прямой СТ треугольник ABC проектируется на треугольник АВТ так, что его проекция будет подобна треугольнику
. Тогда при проектировании на плоскость а параллельно прямой СТ треугольник ABC проектируется на треугольник АВТ так, что его проекция будет подобна треугольнику 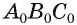 . В частности, за изображение прямоугольного, равнобедренного, равностороннего треугольников можно принять любой треугольник.
. В частности, за изображение прямоугольного, равнобедренного, равностороннего треугольников можно принять любой треугольник.
2.В качестве изображения данного параллелограмма можно взять произвольный параллелограмм.
В самом деле, проекциями равных параллельных отрезков являются равные параллельные отрезки, следовательно, изображением параллелограмма является параллелограмм. В частном случае за изображение прямоугольника, квадрата, ромба можно принять любой параллелограмм.
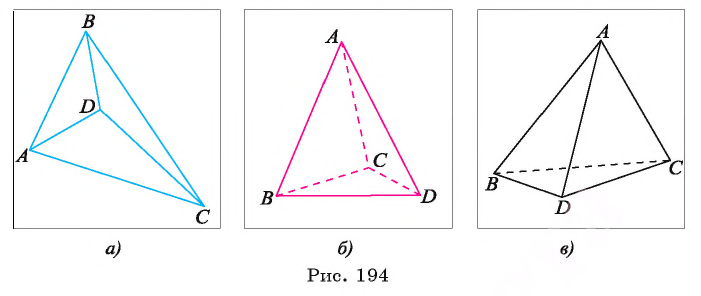
3.При изображении пространственных фигур пользуются тем фактом, что фигуру, состоящую из сторон и диагоналей любого выпуклого или не выпуклого четырехугольника, можно считать изображением треугольной пирамиды при определенном выборе направления проектирования и плоскости, на которую проектируется эта пирамида (рис. 193, в).
Например, фигуры, изображенные на рисунке 194, а, б, в, являются изображениями треугольной пирамиды при соответствующем выборе направления проектирования.
Для построения изображения параллелепипеда 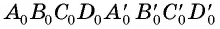 можно воспользоваться тем, что точки
можно воспользоваться тем, что точки 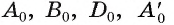 являются вершинами треугольной пирамиды
являются вершинами треугольной пирамиды 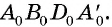 В качестве изображения этих вершин можно взять вершины произвольного четырехугольника
В качестве изображения этих вершин можно взять вершины произвольного четырехугольника 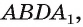 т.е. три отрезка АВ, AD и
т.е. три отрезка АВ, AD и 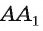 в плоскости изображения с общим концом А, никакие два из которых не лежат на одной прямой, можно принять за изображение ребер
в плоскости изображения с общим концом А, никакие два из которых не лежат на одной прямой, можно принять за изображение ребер 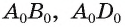
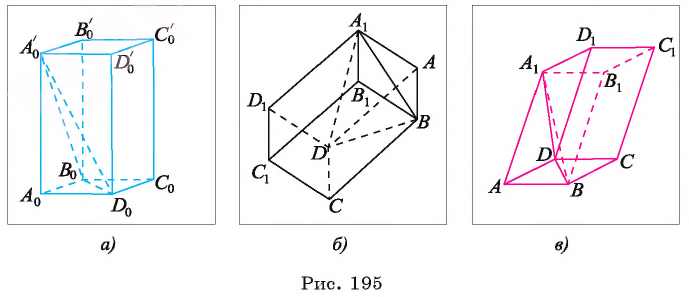
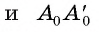 параллелепипеда. Изображения остальных ребер параллелепипеда строятся с использованием свойств, которые сохраняются при параллельном проектировании (все грани параллелепипеда являются параллелограммами, следовательно, их изображения — параллелограммы). На рисунке 195, б, в даны различные изображения параллелепипеда
параллелепипеда. Изображения остальных ребер параллелепипеда строятся с использованием свойств, которые сохраняются при параллельном проектировании (все грани параллелепипеда являются параллелограммами, следовательно, их изображения — параллелограммы). На рисунке 195, б, в даны различные изображения параллелепипеда 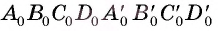 (рис. 195, а).
(рис. 195, а).
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Решение прямоугольных треугольников
- Параллелограмм
- Теорема синусов и теорема косинусов
- Параллельность прямых и плоскостей