Перпендикуляр и наклонная в геометрии - определение и вычисление с примерами решения

Перпендикуляр и наклонная:

Рассмотрим понятия перпендикуляра и наклонной к прямой в плоскости.

Пусть точка О и прямая а лежат в плоскости, а точка О не лежит на прямой а.

Перпендикуляром, проведенным из точки О к прямой а, называется отрезок ОB, такой, что точка B лежит на прямой а и отрезок ОB перпендикулярен прямой а. Точка B называется основанием перпендикуляра.

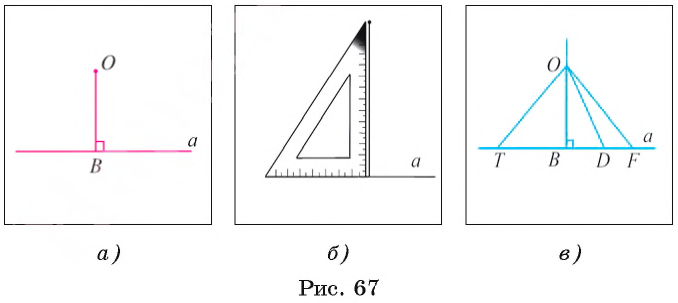
На рисунке 67, а отрезок ОB — перпендикуляр, проведенный из точки О к прямой а.

При изображении перпендикулярных прямых или перпендикуляра пользуются чертежным угольником (рис. 67, б).

Пусть точка B — основание перпендикуляра ОB, проведенного из точки О к прямой а.

Отрезок, соединяющий точку О с любой точкой прямой а, не совпадающей с основанием B перпендикуляра, называется наклонной к прямой а.

На рисунке 67, в изображены наклонные OF, OD и ОТ к прямой а.

Теорема 1 (о существовании единственного перпендикуляра, проведенного из точки к прямой).

Из точки, не лежащей на прямой в плоскости, можно провести единственный перпендикуляр к данной прямой.

Доказательство.

1. Докажем, что такой перпендикуляр существует.

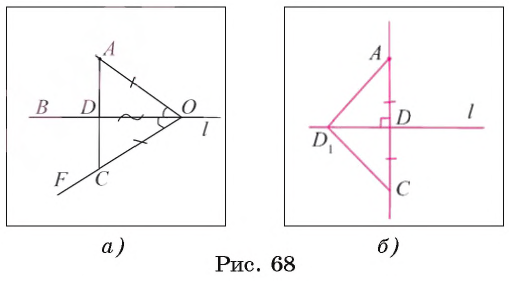
Пусть точка А не принадлежит прямой l. Возьмем на этой прямой некоторую точку О и проведем луч ОА (рис. 68, а). Далее от луча OB в другой полуплоскости отложим угол BOF, равный углу АОВ. На луче OF отложим отрезок ОС, равный отрезку ОА. Пусть точка D — точка пересечения отрезка АС и прямой l. Треугольник AOD равен треугольнику COD по первому признаку равенства треугольников, т. к. АО = ОС, сторона OD — общая,

2. Докажем единственность перпендикуляра.

Воспользуемся методом доказательства от противного. Предположим, что из точки А можно провести еще один перпендикуляр АD к прямой l. Пусть DС — луч, противоположный лучу DА, и DС = DА (рис. 68, б). Треугольники D₁DA и D₁DС равны по первому признаку равенства треугольников, так как DС = DА, сторона DD₁— общая, ADD₁ = CDD₁. Следовательно, AD₁D  = CD₁D. Так как по предположению AD₁D = 90°, то CD₁D = 90°, т. е. угол AD₁C  развернутый и лучи D₁A и D₁C составляют прямую. Таким образом, получаем, что через две точки А и С проходят две прямые, что противоречит аксиоме о существовании единственной прямой, проходящей через две точки. Значит, предположение о том, что из точки можно провести два перпендикуляра к прямой, неверно. Следовательно, такой перпендикуляр единственный.

Теорема доказана.

Теорема 2. Если две прямые плоскости перпендикулярны третьей прямой этой плоскости, то они не пересекаются.

Доказательство.

Пусть прямые а и b перпендикулярны прямой l. Докажем, что прямые а и b не пересекаются. Допустим, что прямые а и b пересекаются в некоторой точке О. Пусть прямые а и b пересекают прямую l в точках F и D соответственно. Тогда получаем, что из точки О к прямой l проведены два перпендикуляра OF и ОD. Это противоречит теореме о существовании единственного перпендикуляра, проведенного из точки к прямой. Значит, наше предположение о том, что прямые а и b пересекаются, неверно. Прямые а и b не пересекаются.

Теорема доказана.