Периодические несинусоидальные напряжения и токи в линейных цепях

Содержание:

Периодические несинусоидальные напряжения и токи в линейных цепях:

Разложение периодических функций в ряд Фурье

До сих пор рассматривались линейные цепи при постоянных и синусоидальных напряжениях и токах; синусоидальная форма кривых позволила применить векторные диаграммы и символический метод, весьма упростившие расчет цепей.

В электротехнике стремятся к синусоидальной форме периодических кривых, так как большинство устройств при этом работает лучше, однако на практике кривые несколько отличаются от синусоид. В устройствах электронной и вычислительной техники и во многих других по принципу их действия напряжения и токи должны быть несинусоидальными. В этих случаях можно использовать изложенные методы расчета цепей при постоянных и синусоидальных напряжениях и токах, если разложить периодические несинусоидальные кривые в ряд Фурье.

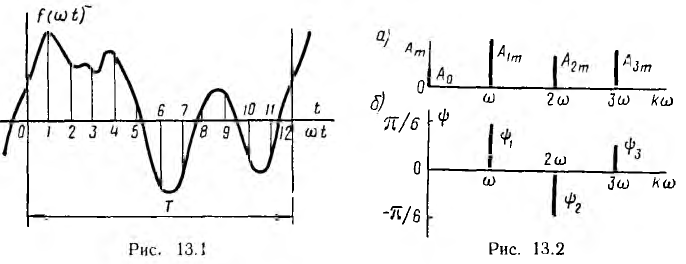
Как известно из математики, периодическая функция f (ωt), удовлетворяющая условиям Дирихле, т. е. имеющая за полный период конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть приближенно представлена тригонометрическим рядом F (ωt). Этот ряд состоит из суммы постоянной составляющей С₀ и синусоид разных частот kω, где k — целые числа, начиная с единицы:

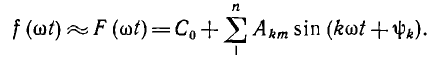
Ряд Фурье может быть записан в другой форме:

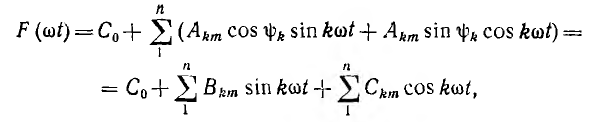
Заданная графически кривая может быть также разложена в ряд Фурье с помощью механических гармоникоанализаторов, основанных на том, что при обводе анализируемой кривой штифтом этого прибора точки его сменной шестерни, соответствующей данному номеру гармоники, описывают замкнутые траектории, площадь внутри которых пропорциональна коэффициентам B_km и С_km этой гармоники. Периодические напряжения и токи могут быть разложены непосредственно электрическими гармоникоанализаторами, основанными на создании в их схеме резонансов для отдельных гармоник.

На практике часто встречаются симметричные кривые; аналитическое разложение их упрощается.

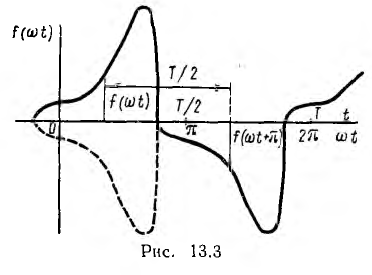
При симметрии относительно оси абсцисс (рис. 13.3) значения ординат кривой повторяются через половину периода с обратным знаком:

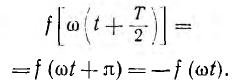
При этом кривая второго полупериода, сдвинутая влево на π, представляет собой зеркальное отображение кривой первого полупериода в оси абсцисс. Очевидно, что при сдвиге начала отсчета времени (начала координат) рассматриваемый вид симметрии сохраняется.

В соответствии с приведенным соотношением в первую форму ряда Фурье для подобных кривых могут входить только те гармоники, для которых

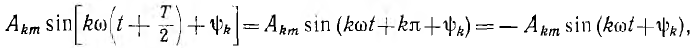
а это имеет место только при нечетном k. Следовательно, кривые, обладающие указанной симметрией, могут содержать только нечетные гармоники и не содержат четных гармоник и постоянной составляющей. В этом случае кривую полностью характеризует один ее полупериод, и для определения коэффициентов разложения достаточно произвести интегрирование за полупериод:

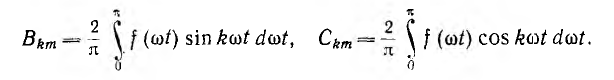
Приближенные формулы (13.1) сохраняют свой вид, но теперь π — число ординат для полупериода.

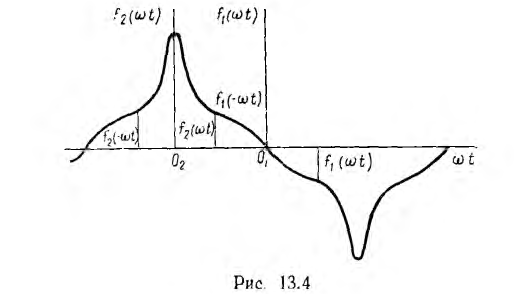
На практике часто встречаются кривые, симметричные относительно оси абсцисс, вид которых полностью характеризуется четвертью ее периода (рис. 13.4). Если выбрать начало координат в точке 0₁ относительно которой ординаты, соответствующие одинаковым по величине, но разным по знаку абсциссам, также равны между собой, но обратны по знаку:

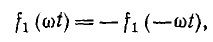
то во вторую форму ряда Фурье для подобных кривых могут входить только те составляющие, для которых

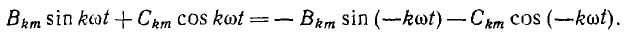
Так как в отличие от синусов косинусы не изменяют своего знака при изменении знака аргумента и, кроме того, рассматриваемая кривая симметрична относительно оси абсцисс, в ней не содержатся ни косинусы, ни постоянная составляющая, а могут содержаться только нечетные синусы:

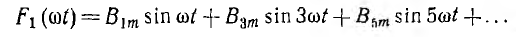
Если для подобной кривой сдвинуть начало координат на 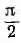в точку О₂ (см. рис. 13.4), кривая будет содержать только нечетные косинусы:

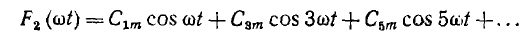
В этих случаях для определения коэффициентов разложения интегрирование достаточно произвести за четверть периода и умножить результат на 4/π. Приближенные формулы (13.1) сохраняют свой вид, но теперь n — число ординат для четверти периода,

При сдвиге начала координат на угол, отличный от π/2, разложение этого вида кривых содержит и нечетные синусы, и нечетные косинусы.

Ряды Фурье для наиболее распространенных в электротехнике периодических функций даны в приложении 3.

Действующее значение и мощность при несинусоидальных напряжениях и токах

Действующее значение несинусоидального тока определяется, как и для синусоидального тока, по равенству средней мощности переменного тока и мощности постоянного тока в том же сопротивлении r:

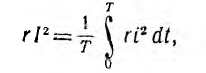
т. е. действующее значение периодического переменного тока

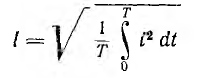
является его среднеквадратичным значением за период. После подстановки в это выражение значения тока i в виде ряда Фурье:

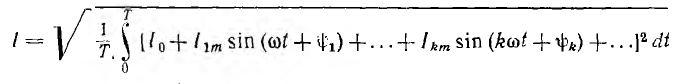
интеграл может быть представлен в виде суммы интегралов вида:

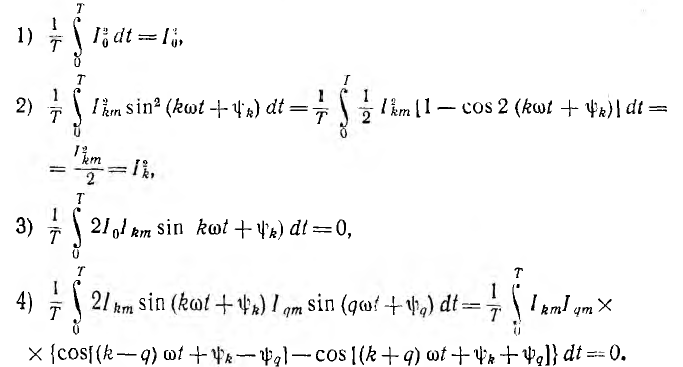
Следовательно,

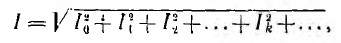
т. е. действующее значение тока равно корню квадратному из суммы квадратов постоянной составляющей I₀ и действующих значений токов всех гармоник, и не зависит от их начальных фаз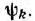

По аналогии действующее значение напряжения

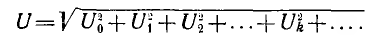
Важной характеристикой кривой является среднее значение ее абсолютной величины за период

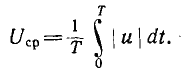
Например, для синусоиды

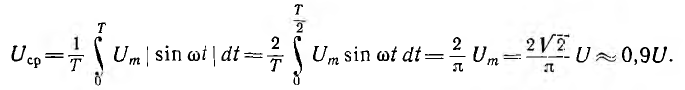
Для характеристики кривых без постоянной составляющей пользуются несколькими коэффициентами. Коэффициент искажения k_u равен отношению действующего значения первой гармоники к действующему значению всей кривой: 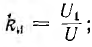в случае синусоиды k_u=1. Коэффициент амплитуды k₁, равен отношению максимального значения U_m к действующему U: 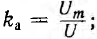для синусоиды 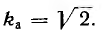Коэффициент формы равен отношению действующего значения U к среднему значению U_ср кривой: 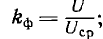для синусоиды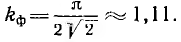

Мгновенная мощность р после разложения напряжения u и тока i в ряды Фурье получает вид:

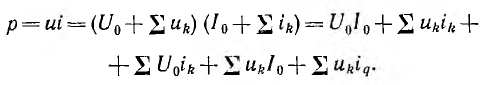
Таким образом, р имеет постоянную составляющую U₀I₀ и синусоидальные составляющие u_ki_k, имеющие частоту 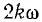и среднее значение 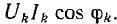Кроме того, в кривой р содержатся синусоидальные составляющие вида 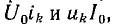имеющие частоту 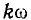, и вида 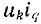, представляющие собой сумму синусоидальных функций частоты (k — q) ω и (k + q) ω, среднее значение которых равно нулю. Следовательно, кривая мгновенной мощности имеет весьма сложную форму, но средняя мощность

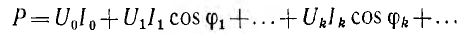
равна сумме средних мощностей, создаваемых одноименными гармониками напряжения и тока.

Если при синусоидальном напряжении и токе полная мощность S — UI и реактивная мощность Q — UI sin ϕ имели определенный физический смысл как амплитуды синусоид соответствующих мгновенных мощностей, то при сложной форме кривых строгие определения S и Q дать невозможно, и они могут быть чисто условными. При отсутствии постоянных составляющих общепринято определение полной мощности как произведения действующих значений напряжения и тока:

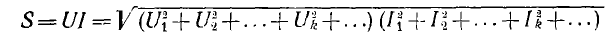
Если по аналогии с активной мощностью под реактивной мощностью понимать алгебраическую сумму реактивных мощностей отдельных гармоник

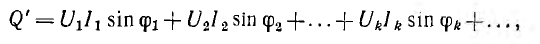
можно показать, что

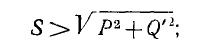
тогда вводят понятие мощности искажения Т, определяемой из соотношения

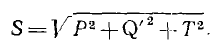
В приближенных расчетах при отсутствии в кривых напряжения и тока постоянных составляющих иногда оперируют с эквивалентными синусоидами, имеющими те же действующие значения напряжения U и тока , что и заданные кривые. Эти синусоиды должны быть сдвинуты на угол ϕ, при котором средняя мощность будет той же, т. е. UI cos ϕ = Р. Тогда cos ф называют коэффициентом мощности, а реактивную мощность определяют из треугольника мощностей как

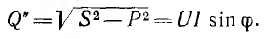
Расчет линейных цепей при несинусоидальных напряжениях и токах

Если напряжение, приложенное к цепи, имеет сложную форму:

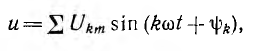
то ток цепи с активным сопротивлением

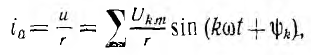
ток цепи с индуктивностью L

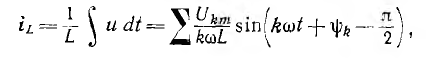
ток цепи с емкостью С

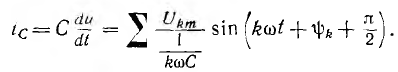
Отсюда видно, что каждой гармонике напряжения соответствует своя гармоника тока, вычисляемая независимо от других гармоник.

При пренебрежении поверхностным эффектом активное сопротивление для всех гармоник одинаково. Индуктивное сопротивление kωL растет, а емкостное 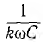убывает пропорционально порядку гармоники.

Таким образом, для расчета сложных линейных цепей может быть применен метод наложения: после разложения кривых заданных напряжений и токов в ряд Фурье они записываются в его первой форме и задача решается для каждой гармоники в отдельности; при этом сопротивления ветвей для каждой гармоники в общем случае будут различными. Задачи для отдельных гармоник решаются однотипно и при их решении может быть использован весь аппарат теории синусоидальных токов — векторные диаграммы, символический метод и т. д. Затем можно произвести наложение решений для мгновенных значений отдельных гармоник — напряжений и токов каждой ветви и вычислить их действующие значения и мощность.

Например, в цепи, состоящей из последовательного соединения сопротивления r, индуктивности L и емкости С (см. рис. 7.1, а), полное сопротивление и угол сдвига фаз для гармоники порядка k будут:

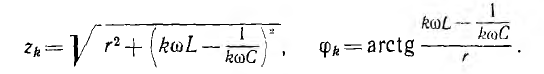
Для одной из гармоник эта цепь может оказаться в резонансе; тогда, если порядок этой гармоники т, то

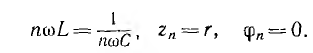
Для остальных гармоник: при k < n

при k > 0.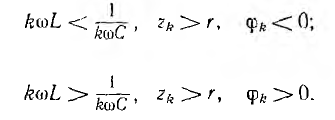

Значение индуктивности, при которой происходит резонанс,

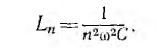
Поэтому если в цепи, питаемой несинусоидальным напряжением, увеличивать L, начиная от нуля, в ней будет происходить резонанс на отдельных гармониках, начиная с высшей. При достаточно малом r ток резонансной гармоники будет относительно большим, и кривая I(L) зависимости действующего значения тока от индуктивности, так как 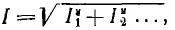будет иметь ряд максимумов, соответствующих отдельным гармоникам напряжения. Аналогичная зависимость получится и при изменении емкости.

Для расчета более сложной цепи при заданном в виде ряда Фурье напряжении или токе, например изображенной на рис. 13.5, целесообразно применять символический метод. Решая эту задачу методом преобразования, сначала подсчитывают комплексное сопротивление всей цепи для отдельных гармоник по заданным r, L и C и основной частоте ω; для постоянной составляющей оно равно r, для гармоники k

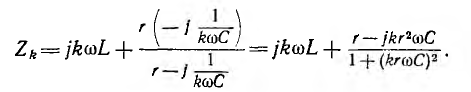
Затем по заданным комплексам гармоник напряжения всей цепи вычисляются комплексы 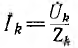гармоник тока всей цепи, а после этого — комплексы гармоник напряжения правого участка

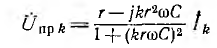
и токов в разветвлении. От символической записи легко перейти к мгновенным значениям для отдельных гармоник и к мгновенному значению всей величины — сумме гармоник, а также к действующему значению.

Средняя (активная) мощность рассматриваемой цепи равна 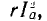, где I_а — действующее значение тока ветви с сопротивлением r.

Влияние параметров цепи на форму кривой напряжения или токе. Резонансные фильтры

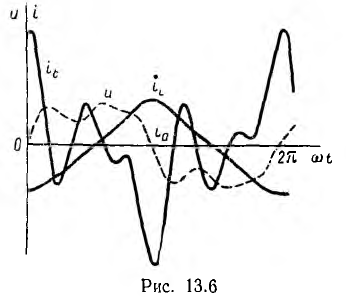
Гармоники тока i_л цепи с сопротивлением r, независящим от частоты, пропорциональны одноименным гармоникам напряжения и совпадают с ними по фазе; следовательно, результирующие кривые напряжения и тока i_л будут подобны (рис. 13.6).

Отношение амплитуды тока гармоники порядка k и амплитуды тока основной гармоники цепи с индуктивностью L:

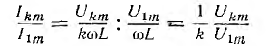
будет в k раз меньше отношения амплитуд гармоник напряжения. Спедовательно, роль высших гармоник в кривой тока будет меньшей,

ем в кривой напряжения, и кривая индуктивного тот i_L будет ближе синусоиде, чем кривая напряжения (рис. 13.6). Отношение амплитуд гармоник тока цепи с емкостью C:

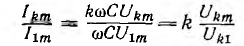
будет в k раз больше отношения амплитуд гармоник напряжения. Следовательно, роль высших гармоник в кривой тока будет больше, чем в кривой напряжения, и кривая емкостного тока i_c будет больше отличаться от синусоиды, чем кривая напряжения.

Свойство цепей переменного тока изменять форму кривой используется в электрических фильтрах.

Г-образный фильтр (рис. 13.7) предназначается для уменьшения переменной составляющей в напряжении и токе приемников, питаемых от электрических генераторов постоянного тока и выпрямителей, которые дают на выходе не постоянное, а пульсирующее напряжение (рис. 13.8). Считая в первом приближении эти пульсации синусоидальными, форму кривой характеризуют коэффициентом пульсации k_п равным отношению максимального значения переменной слагающей U_m напряжения к среднему его значению U₀, т. е.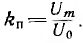

Пренебрегая активным сопротивлением катушки фильтра и считая, что сопротивление конденсатора 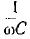во много раз меньше сопротивления r приемника, можно пренебречь переменной составляющей тока приемника и сделать расчет для холостого хода.

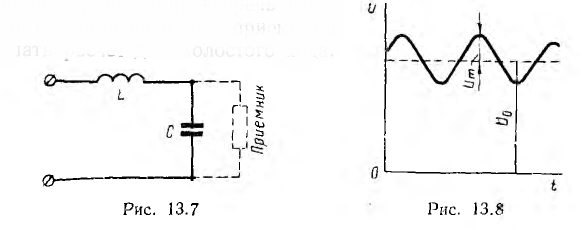
Постоянные составляющие напряжения и тока сохраняются, так как аля них сопротивление катушки равно нулю, а конденсатора — бесконечности. Амплитуда переменной составляющей напряжения на конденсаторе, а следовательно, и на приемнике

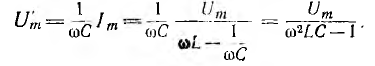
Поэтому коэффициент пульсации напряжения приемника

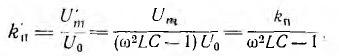
т. е. уменьшится в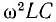 — 1 раз по сравнению с коэффициентом пул сации k_n у генератора; для высших гармоник фильтр будет уменьшат пульсации еще в большей степени.

Если сглаживающее действие одного Г-образного элемента недоел точно, можно включить последовательно несколько ступеней.

Для ослабления какой-либо гармоники в кривой тока по сравнении с кривой входного напряжения последовательно с приемником можно включить фильтр с параллельным соединением катушки индуктивности и конденсатора настроенных в резонанс на эту гармонику так как сопротивление фильтра для нес будет наибольшим.

Для выделения какой-либо гармоники в кривой тока по сравнению с кривой входного напряжения последовательно с приемником можно включить фильтр с последовательным соединением катушки индуктивности и конденсатора, настроенных в резонанс на эту гармонику, так как сопротивление фильтра для нее будет наименьшим.

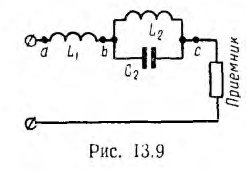
На рис. 13.9 изображена схема фильтра, предназначенного для выделения гармоники порядка q и ослабления гармоники порядка s. В контуре bc должен иметь место резонанс токов для гармоники порядка s:

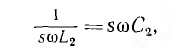
а в участке цепи ас — резонанс напряжений для гармоники порядка q:

откуда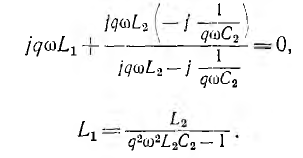

Высшие гармоники в трехфазных цепях

Здесь рассматривается случай, когда причиной появления высших гармоник в кривых напряжений и токов трехфазных цепей является источник электрической энергии, фазные э. д. с. которого несинусоидальны. Так как трехфазные генераторы имеют симметричное устройство, кривые их э. д. с. симметричны относительно оси абсцисс и поэтому содержат только нечетные гармоники.

Сложная форма кривых э. д. с. и токов в трехфазных системах как правило, ухудшает работу электродвигателей и других приемников, вызывает помехи в близлежащих линиях связи и т. п.

Пусть трехфазная цепь симметрична, т. е. кривые э. д. с. и, соответственно, токов всех трех фаз имеют одинаковую форму и лишь сдвинуты во времени на треть периода всей кривой. В этом случае одномоментные гармоники всех трех фаз одинаковы по амплитуде, но сдвинуты друг относительно друга по фазе на угол 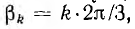где k — эмер гармоники. Следовательно, первые гармоники сдвинуты на гол 2π/3, третьи на 3•2π/3, т. е. совпадают по фазе, пятые на 6—1) 2π/3, что эквивалентно сдвигу на — 2π/3, седьмые на (6+1) 2π/3, . е. на 2π/3 и т. д. Поэтому гармоники 1,7, 13,... отдельных фаз, двинутые по фазе на угол 2π/3, образуют прямые системы, как показано на рис. 13.10, а для первых гармоник э. д. с. трехфазной системы. Гармоники 5, 11, 17, ..., сдвинутые по фазе на угол — 2π/3, образуют обратные системы (рис. 13.10, б для пятых гармоник). Гармоники 3, 9, 15, ..., кратные трем, совпадают по фазе и, следовательно, образуют нулевые системы (рис. 13.10, в для третьих гармоник).

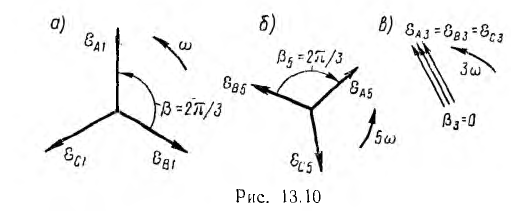
Не следует смешивать только что рассмотренные системы с симметричными составляющими несимметричной трехфазной цепи при синусоидальном токе  там векторы раскладываются на прямую, обратную и нулевую системы одной и той же частоты, а здесь же число систем каждого вида не ограничено, и каждая система имеет свою частоту. Эти системы имеют следующие свойства, вытекающие из рис. 13.10: 1) сумма векторов прямой и обратной систем равна нулю, нулевой системы — утроенному вектору; 2) разность двух векторов в прямой и обратной системах по величине равна вектору, умноженному на 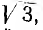, в нулевой системе — нулю. Отсюда вытекает ряд важных свойств трехфазных цепей с напряжениями и токами сложной формы.

Если трехфазный генератор, фазные э. д. с. которого содержат все три вида гармоник, соединен звездой, гармоники нулевой системы 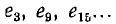выпадают из линейных э. д. е., равных разности фазных, а следовательно, и из линейных напряжений. Тогда действующие значения фазных и линейных э. д. с. будут соответственно равны:

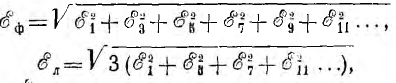
их отношение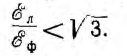

Если генератор соединен треугольником, его фазы образуют замкнутый контур, в котором суммируются э. д. с. фаз. Прямые и обратные системы э. д. с. в сумме дадут нуль, сумма гармоник э. д. с. нулевых систем, равная 3 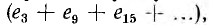вызывает ток, потери и падет напряжения во внутреннем сопротивлении контура, в точности сравнение этой э. д. с. В результате в фазных напряжениях генератора, равные: в схеме треугольника линейным напряжениям, гармоники нулевой системы будут также отсутствовать.

При соединении генератора и приемника треугольником или звездой без нулевого провода линейные токи трехпроводной линии также к могут содержать гармоник, кратных трем, так как по первому закон Кирхгофа сумма линейных токов должна быть равна нулю.

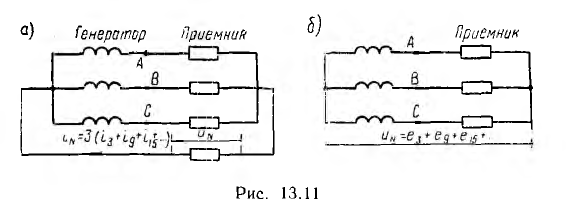
Это ограничение отсутствует при наличии нулевого провод; (рис. 13.11, а), и в линейных токах появляются также гармоники кратные трем: 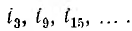Так как ток нулевого провода равен сумме линейных токов, то при одинаковой нагрузке фаз суммы токов прямой и обратной систем будут равны нулю и в нулевом проводе будут только токи нулевых систем. Мгновенное и действующее значение тока нулевого провода соответственно равны:

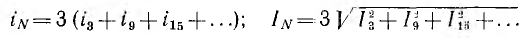
При этом узловое напряжение, т. е. напряжение на сопротивлении нулевого провода, будет также состоять из гармоник, кратных трем.

В системе без нулевого провода (рис. 13.11, б) узловое напряжение, равное разности между напряжениями какой-либо фазы генератора и одноименной фазы приемника, будет равно:

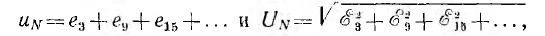
так как в фазных напряжениях приемника гармоники, кратные трем, должны отсутствовать, потому что их нет в кривых тока.

Роль высших гармоник в трехфазных цепях видна на примере двигателя трехфазного тока, работающего на принципе вращающегося магнитного поля: гармоники токов обратных систем создают поля вращающиеся в обратном направлении и тем самым уменьшающих полезный вращающий момент двигателя.