
Периодические дроби с примерами решения
Каждое рациональное число является действительным числом, а поэтому может быть записано в виде десятичной дроби — конечной или бесконечной. Хорошо известно, как это делается, когда 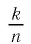
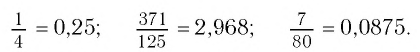
Применим теперь этот метод обращения обыкновенной дроби в десятичную к числу 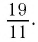 Для этого разделим
Для этого разделим 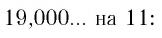
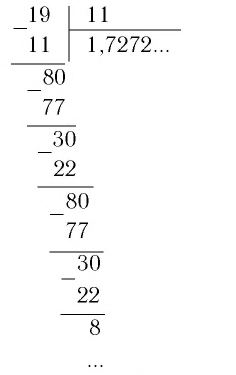
Таким образом, 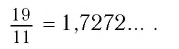
Бесконечная дробь, стоящая в правой части этого равенства, содержит периодически повторяющуюся группу цифр 72. Эта группа цифр называется периодом дроби, а сама дробь — периодической. При записи таких дробей период заключают в скобки и пишут один раз:
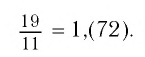
(Читается: «Одна целая семьдесят два в периоде».)
Еще один пример: 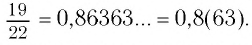
(Читается: «Нуль целых восемь десятых шестьдесят три в периоде».)
Приписывая к конечной десятичной дроби бесконечно много нулей, мы получаем бесконечную десятичную дробь. Поэтому конечные десятичные дроби тоже считаются периодическими с периодом 0. (При делении двух натуральных чисел не могут получиться дроби с числом 9 в периоде, поэтому в школьном курсе алгебры их не рассматривают.)
Приведенные примеры дают возможность догадаться, что каждое рациональное число записывается в виде бесконечной десятичной периодической дроби.
Чтобы в этом убедиться, заметим, что для обращения обыкновенной дроби 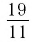 в десятичную мы на каждом шаге остаток от деления (он был равен либо 8, либо 3) умножали на 10 и делили на 11. Но при делении на 11 вообще возможны лишь 11 различных остатков. Значит, на каком-то шаге остаток обязательно повторится (в нашем примере это случилось на третьем шаге), и поэтому в результате деления должна получиться периодическая дробь.
в десятичную мы на каждом шаге остаток от деления (он был равен либо 8, либо 3) умножали на 10 и делили на 11. Но при делении на 11 вообще возможны лишь 11 различных остатков. Значит, на каком-то шаге остаток обязательно повторится (в нашем примере это случилось на третьем шаге), и поэтому в результате деления должна получиться периодическая дробь.
Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число.
Каждую периодическую десятичную дробь можно рассматривать либо как сумму бесконечно убывающей геометрической прогрессии, либо как сумму конечной десятичной дроби и сумму бесконечно убывающей геометрической прогрессии. Это позволяет представлять периодические десятичные дроби в виде обыкновенных дробей.
Пример №1
Обратить в обыкновенную дробь число:
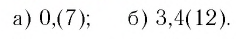
Решение:
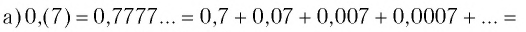
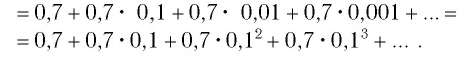
Таким образом, число 0,(7) есть 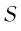 — сумма бесконечно убывающей геометрической прогрессии
— сумма бесконечно убывающей геометрической прогрессии 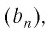 где
где 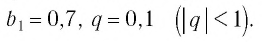
Значит, 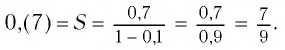
б) 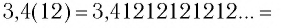
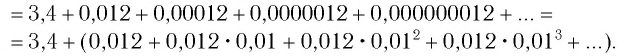
Сумму, стоящую в скобках, обозначим буквой S. Тогда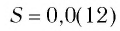 есть сумма бесконечно убывающей геометрической прогрессии с первым членом
есть сумма бесконечно убывающей геометрической прогрессии с первым членом 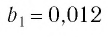 и знаменателем
и знаменателем 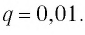
Значит, 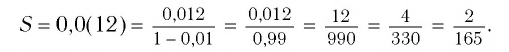
Таким образом,
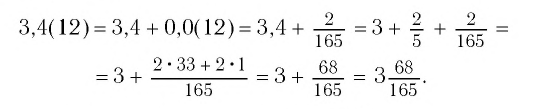
Ответ: 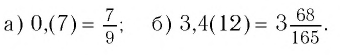
Изучением периодических дробей занимался великий немецкий математик К- Ф. Гаусс (1777—1855). Уже в детстве он делил единицу на все подряд простые числа р из первой тысячи. При этом Гаусс подметил, что, начиная с какого-то места, десятичные знаки начинают повторяться, т. е. получаются периодические десятичные дроби. А периоды некоторых дробей достигали нескольких сотен десятичных знаков. Рассматривая эти примеры, Гаусс установил, что число цифр в периоде всегда является делителем числа 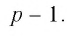
Пример №2
Найти значение выражения:
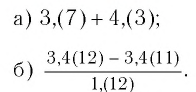
Решение:
Обратив каждое из чисел в обыкновенную дробь (см. пример 1), получим: 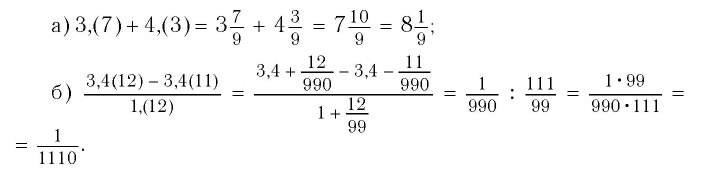
Ответ: 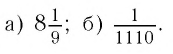
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Степень с рациональным показателем
- Степень с действительным показателем
- Логарифм - формулы, свойства и примеры
- Корень из числа - нахождение и вычисление
- Тождества с корнями, содержащие одну переменную
- Действия с корнями нечетной степени
- Действия с корнями четной степени
- Бесконечно убывающая геометрическая прогрессия