
Пересечения поверхностей с прямой и плоскостью с примерами
Содержание:
В пересечении поверхности плоскостью образуется линия называемая сечением. Сечением многогранника является многоугольник. Для его построения необходимо определить точку пересечения каждого ребра с плоскостью и соединить полученные точки с учетом видимости. Фактически решение такой задачи рассматривалось в лекции 2 (рисунок 2.13).
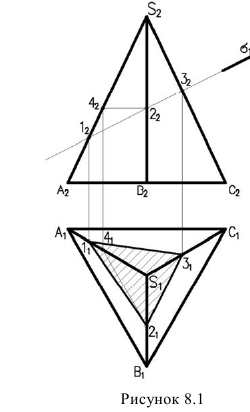
В данной лекции рассмотрим построение линии сечения пирамиды плоскостью 
Так как плоскость б фронтально-проецирующая, фронтальная проекция сечения совпадает с плоскостью  . Точки 1,2,3 - точки пересечения боковых ребер пирамиды с плоскостью
. Точки 1,2,3 - точки пересечения боковых ребер пирамиды с плоскостью  . Поэтому достаточно построить горизонтальные проекции этих точек. Точки
. Поэтому достаточно построить горизонтальные проекции этих точек. Точки 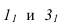 находятся по вертикальным линиям связи на ребрах
находятся по вертикальным линиям связи на ребрах 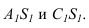 Так как ребро SB профильное, для нахождения точки
Так как ребро SB профильное, для нахождения точки 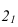 через проекцию
через проекцию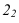 проведем прямую
проведем прямую 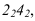 , лежащую на грани ASB и параллельную АВ. Построив, горизонтальную проекцию определим положение проекции
, лежащую на грани ASB и параллельную АВ. Построив, горизонтальную проекцию определим положение проекции 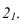 Соединив, полученные точки, получим треугольник. Треугольник видимый, т.к. все грани пирамиды видимые.
Соединив, полученные точки, получим треугольник. Треугольник видимый, т.к. все грани пирамиды видимые.
Пересечение кривых поверхностей плоскостью. Конические сечения
В зависимости от положения секущей плоскости, различают следующие виды конических сечений (рисунок 8.2):
- I - окружность - секущая плоскость перпендикулярна оси.
- II - треугольник - секущая плоскость проходит через вершину конуса.
- III - эллипс - секущая плоскость пересекает все образующие конуса
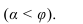
- IV - парабола - секущая плоскость параллельна образующей конуса
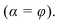
- V - гипербола - секущая плоскость параллельна двум образующим конуса (а >
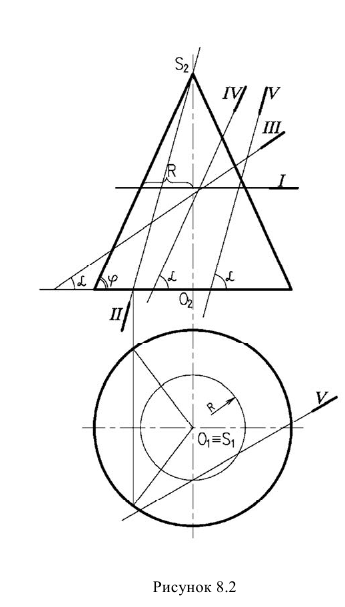
Построение линии сечения конуса по окружности и треугольнику не вызывает затруднений. Для окружности - замеряем радиус, для треугольника - находим точки пересечения с основанием. Построения показаны на рисунок 8. 2.
Для построения сечений конуса по эллипсу, параболе, гиперболе, необходимо определить несколько точек, принадлежащих линии сечения. Для нахождения этих точек используется метод плоскостей посредников.
Алгоритм решения задачи состоит в следующем:
- а) проводят плоскости посредники;
- б) строят линии пересечения посредников с данной поверхностью и с плоскостью;
- в) определяют точки пересечения между собой полученных линий;
- г) соединяют полученные точки с учетом видимости.
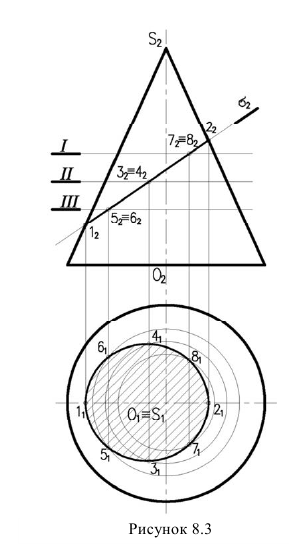
Для примера рассмотрим построение конуса по эллипсу (рисунок 8.3). Т.к. плоскость  фронтально-проецирующая, необходимо построить горизонтальную проекцию сечения. В первую очередь строятся опорные точки сечения, в данном случае высшая и низшая точка сечения, лежащая на контурных образующих (1 и 2). 1,2 - большая ось эллипса. Чтобы сечение получилось правильным, необходимо найти положение малой оси 3,4. Для нахождения горизонтальной проекции
фронтально-проецирующая, необходимо построить горизонтальную проекцию сечения. В первую очередь строятся опорные точки сечения, в данном случае высшая и низшая точка сечения, лежащая на контурных образующих (1 и 2). 1,2 - большая ось эллипса. Чтобы сечение получилось правильным, необходимо найти положение малой оси 3,4. Для нахождения горизонтальной проекции  через фронтальные проекции точек проводим вспомогательную горизонтальную плоскость посредник, которая рассекает конус по окружности. Таким же образом строим промежуточные точки 5,6,7,8. Полученные точки соединяем плавной кривой линией.
через фронтальные проекции точек проводим вспомогательную горизонтальную плоскость посредник, которая рассекает конус по окружности. Таким же образом строим промежуточные точки 5,6,7,8. Полученные точки соединяем плавной кривой линией.
Аналогично строятся линии пересечения других поверхностей плоскостями. Гораздо проще строить сечения поверхностей, проецирующими плоскостями, поэтому, если задана плоскость общего положения, имеет смысл выполнить замену плоскостей проекций, перпендикулярно заданной плоскости, а затем уже строить сечение.
Пересечение примой линии с поверхностью
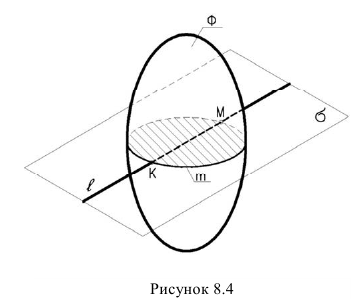
Для определения точек пересечения прямой линии с поверхностью применяется метод вспомогательных секущих плоскостей (рисунок 8.4)
Алгоритм решения задачи следующий:
- Через прямую
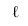 проводим вспомогательную секущую плоскость
проводим вспомогательную секущую плоскость 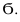
- Строим линию пересечения m плоскости 6 с заданной поверхностью Ф.
- Определяем точки пересечения К и М прямой
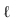 с построенной линией пересечения т. Это и будут искомые точки пересечения прямой
с построенной линией пересечения т. Это и будут искомые точки пересечения прямой  с поверхностью.
с поверхностью. - Определяем видимость прямой. Нужно подчеркнуть, что вспомогательная плоскость выбирается такой, чтобы сечение поверхности было простейшим.
Рассмотрим несколько примеров на определение точек пересечения прямой с поверхностью.
Примеры построении пересечение примой с различными поверхностями
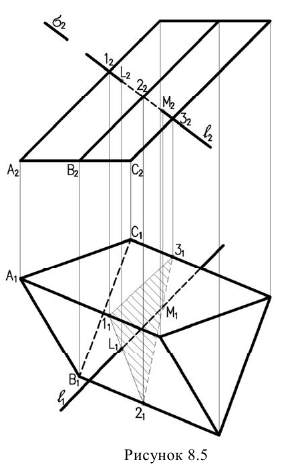
Пример 1. Построить точки пересечения прямой  с поверхностью наклонной трехгранной призмы (рисунок 8.5).
с поверхностью наклонной трехгранной призмы (рисунок 8.5).
Последовательность решения следующая:
- Через прямую
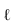 проводим вспомогательную фронтально-проецирующую плоскость
проводим вспомогательную фронтально-проецирующую плоскость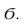
- Строим линию пересечения плоскости
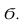 и призмы. Сечением является треугольник 1, 2, 3.
и призмы. Сечением является треугольник 1, 2, 3. - Определяем точки пересечения прямой
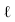 с треугольником сечения (точки L и М).
с треугольником сечения (точки L и М). - Определяем видимость прямой
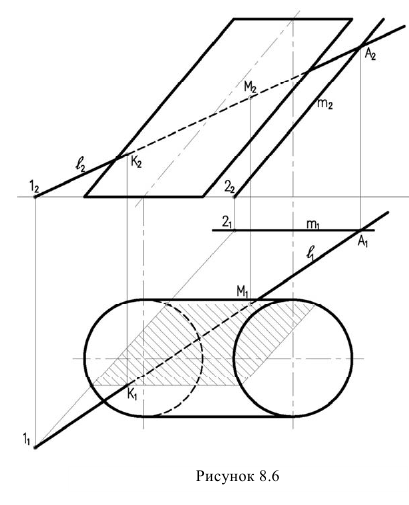
Пример: Поострить точки пересечения прямой с поверхностью наклонного цилиндра (рисунок 8.6).
с поверхностью наклонного цилиндра (рисунок 8.6).
Ход решения:
- Через прямую
 проводим вспомогательную плоскость
проводим вспомогательную плоскость 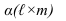 параллельную образующим цилиндра. Плоскость а - общего положения, где m параллельна образующим цилиндра.
параллельную образующим цилиндра. Плоскость а - общего положения, где m параллельна образующим цилиндра. - Строим линию пересечения плоскости а с поверхностью цилиндра. Плоскость параллельная образующим цилиндра рассечет цилиндр но параллелограмму. Для его построения определяем линию пересечения 1,2 плоскости а с плоскостью основания цилиндра. Из точек пересечения линии 1,2 с окружностью основания проводим образующие цилиндра.
- Определяем точки пересечения
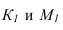 прямой
прямой 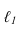 с линией сечения. Фронтальные проекции точек определяем но линиям связи.
с линией сечения. Фронтальные проекции точек определяем но линиям связи. - Устанавливаем видимость прямой.
Пример: Построить точки пересечения прямой с поверхностью конуса (рисунок 8.7)
Ход решения.
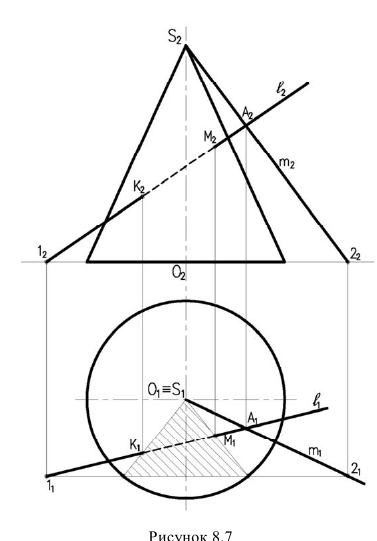
- Через прямую
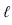 проводим плоскость
проводим плоскость 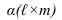 общего положения проходящую через вершину конуса. Такая плоскость пересекает конус но треугольнику.
общего положения проходящую через вершину конуса. Такая плоскость пересекает конус но треугольнику. - Строим линию сечения конуса плоскостью а. Для этого определяем линию пересечения плоскости а с плоскостью основания конуса (точки 1 и 2, соответственно точки пересечения прямых
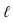 и m c плоскостью основания). Горизонтальная проекция линии пересечения 1,2 пересекает окружность основания. Полученные точки соединяем с вершиной конуса.
и m c плоскостью основания). Горизонтальная проекция линии пересечения 1,2 пересекает окружность основания. Полученные точки соединяем с вершиной конуса. - Определяем точки
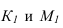 пересечения прямой
пересечения прямой 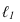 с полученным сечением. Фронтальные проекции определяем по линиям связи.
с полученным сечением. Фронтальные проекции определяем по линиям связи.
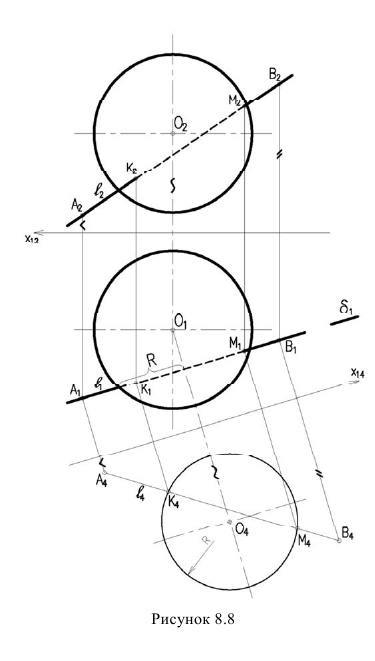
Пример: Построить точки пересечения прямой 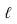 с поверхностью сферы (рисунок 8.8)
с поверхностью сферы (рисунок 8.8)
Последовательность решения:
- Через прямую
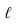 проводим горизонтально-проецирующую плоскость
проводим горизонтально-проецирующую плоскость 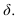
- Для построения линия пересечения сферы плоскостью а выполняем замену фронтальной плоскости проекций
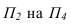 параллельную плоскости
параллельную плоскости 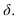 Строим окружность радиуса R (фигура сечения) и новую проекцию прямой
Строим окружность радиуса R (фигура сечения) и новую проекцию прямой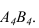
- Определяем точки пересечения
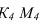 прямой
прямой 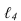 и окружности сечения. Далее, используя линии проекционной связи строим проекции точек
и окружности сечения. Далее, используя линии проекционной связи строим проекции точек 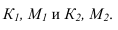
- Определяем видимость прямой
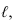
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |