Пересечения криволинейных поверхностей в начертательной геометрии с примером

Содержание:

Возможные случаи пересечения криволинейных поверхностей:

Существуют четыре варианта пересечения двух поверхностей.

Проницание

Все образующие первой поверхности (цилиндра) пересекаются со второй поверхностью, но не все образующие второй поверхности пересекаются с первой. В этом случае линия пересечения поверхностей распадается на две замкнутые кривые линии (рис. 5.43).

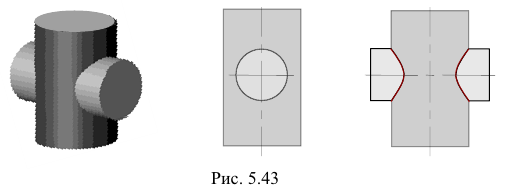
Врезание

Не все образующие той и другой поверхности пересекаются между собой. В этом случае линия пересечения - одна замкну­ тая кривая линия (рис. 5.44).

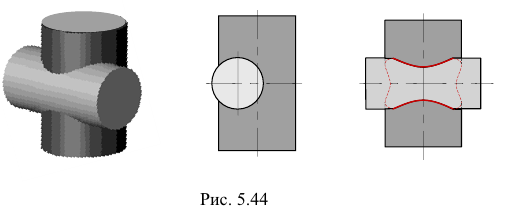
Одностороннее касание

Все образующие одной поверхности пересекаются со второй, но не все образующие второй поверхности пересекаются с первой. Поверхности имеют в одной точке (точка К на рис. 5.45) общую плоскость касания. Линия пересечения распадается на две замкнутые кривые линии, пересекающиеся в точке касания.

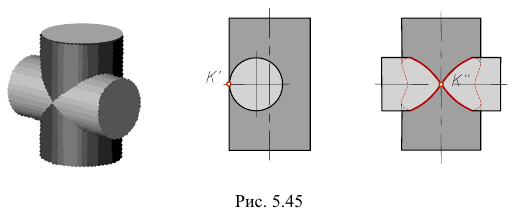
Двойное касание

Все образующие обеих поверхностей пересекаются между собой. Пересекающиеся поверхности имеют две общие касательные плоскости. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точках касания (рис. 5.46).

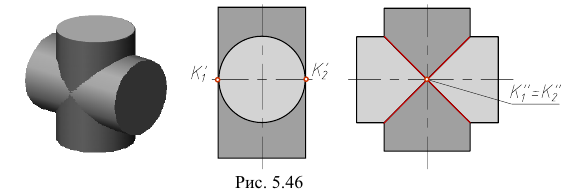
Пересечение поверхностей второго порядка

В общем случае две поверхности второго порядка пересекаются по пространственной кривой четвертого порядка. Следует отметить, что при некоторых особых положениях относительно друг друга поверхности второго порядка могут пересекаться по плоским кривым второго порядка, то есть пространственная кривая пересечения распадается на две плоские кривые.

• Заказать чертежи

Теорема о двойном касании

Если две поверхности второго порядка имеют две общие точки (точки касания), то линия их взаимного пересечения распадается на две плоские кривые второго порядка. Причем плоскости этих кривых пройдут через прямую, соединяющую точки касания.

На рис. 5.47 показано построение линии пересечения поверхно­стей прямого кругового цилиндра и эллиптического конуса. Линии пересечения — эллипсы - лежат в профильно-проецирующих плоскостях S и Т, проходящих через прямую 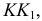соединяющую точки касания.

Теорема Монжа

Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их взаимного пересечения распадается на две плоские кривые. Плоскости этих кривых пройдут через прямую, соединяющую точки пересечения линий касания.

Если оси пересекающихся поверхностей вращения параллельны какой - либо плоскости проекций, то на эту плоскость кривые линии проецируются в прямые.

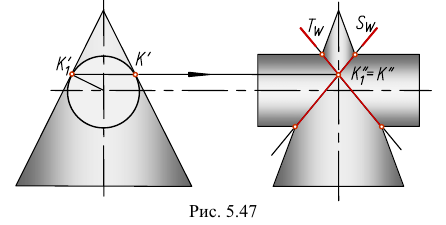
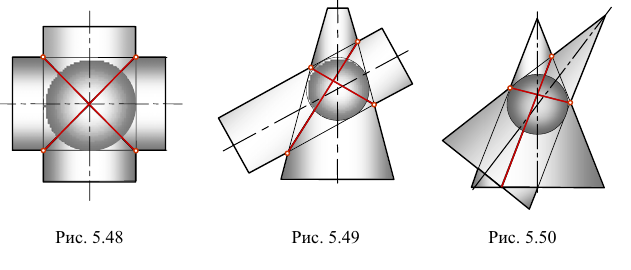
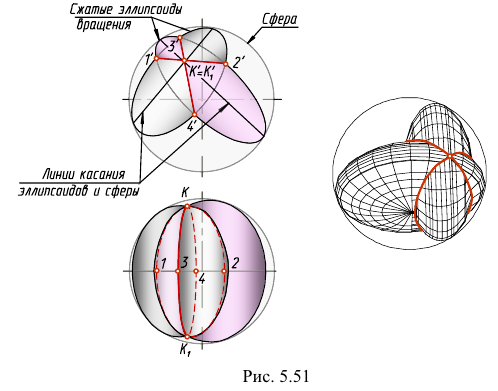
На рис. 5.48 - 5.50 приведены примеры построения линий пересе­чения поверхностей на основании теоремы Монжа, где два цилиндра, цилиндр и конус и два конуса описаны вокруг сферы, а на рис. 5.51 приведен пример построения линии пересечения двух сжатых эллипсоидов вращения, вписанных в сферу.