Пересечение прямой с поверхностью в начертательной геометрии с примерами

Содержание:

Пересечение прямой с поверхностью:

Рассмотрим три варианта, а соответственно и три алгоритма решения задачи по определению точки пересечения прямой с поверхностью:

1. Прямая — проецирующая, поверхность – общего положения;
2. Прямая — общего положения, поверхность – проецирующая;
3. Прямая и поверхность — общего положения.

Пересечение проецирующей прямой с поверхностью общего положения

При решении задач на определение точек пересечения проецирующей прямой с поверхностью общего положения используется собирательное свойство вырожденной проекции проецирующей прямой.

Задача:

На эпюре Монжа построить проекции точек пересечения проецирующей прямой l с поверхностью общего положения

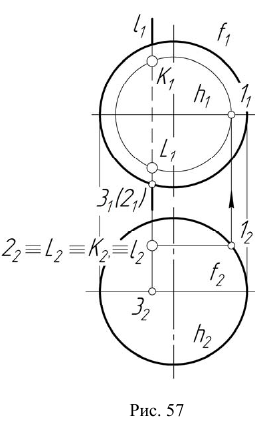
При решении задачи используется алгоритм построения точки, принадлежащей поверхности.

Алгоритм решения

1. Так как прямая 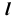горизонтально- проецирующая, то вторые проекции точек пересечения прямой с поверхностью сов- падают с вырожденной проекцией прямой .

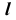Отметим горизонтальные проекции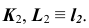

2. Фронтальные проекции 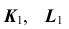определим из условия принадлежности точек K, L поверхности 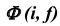(задача 5).

Видимость прямой 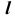относительно поверхности 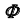при проецировании на фронтальную плоскость проекций опре- делим с помощью конкурирующих то- чек 2 и 3.

Пересечение прямой общего положения с проецирующей поверхностью

При решении задач на определение точек пересечения прямой общего положения с проецирующей поверхностью используется собирательное свойство вырожденной проекции проецирующей поверхности.

Задача:

На эпюре Монжа построить проекции точек пересечения прямой общего положения 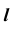с проецирующей поверхностью 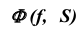(рис. 58).

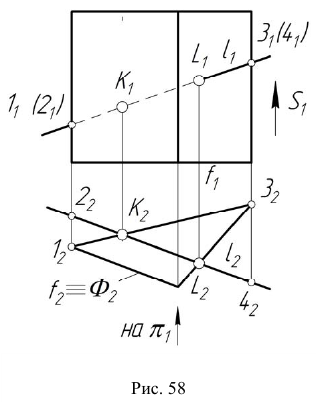
Алгоритм решения

1. Так как точки K, L — общие для прямой и поверхности, а поверхность 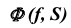—горизонтально-проецирующая, проекции 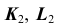определим на пересечении горизонтальных проекций прямой и поверхности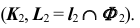
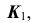
2. Фронтальные проекции 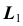определим по принадлежности точек K, L прямой 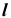(задача 1). Видимость прямой 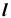относительно поверхности 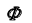при проецировании на фронтальную плоскость проекций определим с помощью конкурирующих точек 1, 2 и 3, 4.

Пересечение прямой общего положения с поверхностью общего положения

Для построения точки пересечения прямой общего положения 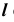с поверхностью общего положения 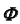выполним следующие операции.

1. Заключим прямую 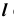во вспомогательную плоскость 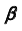(рис. 59). Как правило, плоскость 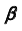— проецирующая плоскость.
2. Построим линию пересечения заданной поверхности 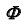и вспомогательной плоскости 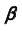— линию m.
3. Определим точку (точки) пересечения прямой 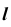с построенной линией m.

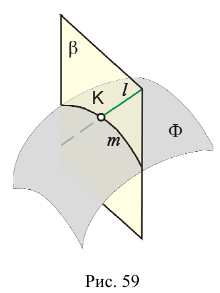
Так как линия m принадлежит заданной поверхности 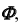точка K будет искомой точкой пересечения прямой 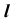с поверхностью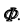

Перед решением задачи по определению точки пересечения прямой общего положения с поверхностью общего положения рассмотрим отдельно реализацию на эпюре Монжа п. 2 — построение линии пересечения проецирующей плоскости с поверхностью общего положения.

Задача:

На эпюре Монжа построить проекции линии пересечения проецирующей плоскости 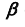с поверхностью общего положения 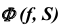(рис. 60). При решении этой задачи используем собирательное свойство вырожденной проекции проецирующей плоскости.

• Заказать чертежи

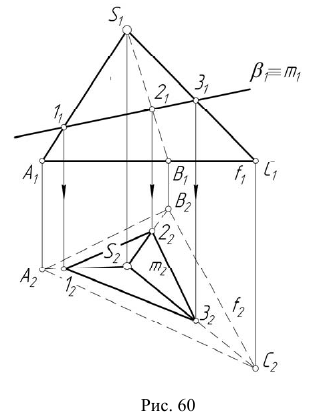
Алгоритм решения

1. Определяем фронтальную проекцию линии m. Так как плоскость 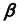— фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости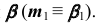
2. Горизонтальную проекцию линии m строим, исходя из условия принадлежности ее поверхности

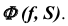
Задача:

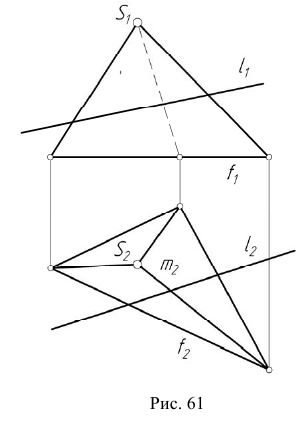
Построить проекции точек пересечения прямой общего положения 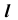с поверхностью общего положения 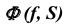(рис. 61).

Алгоритм решения

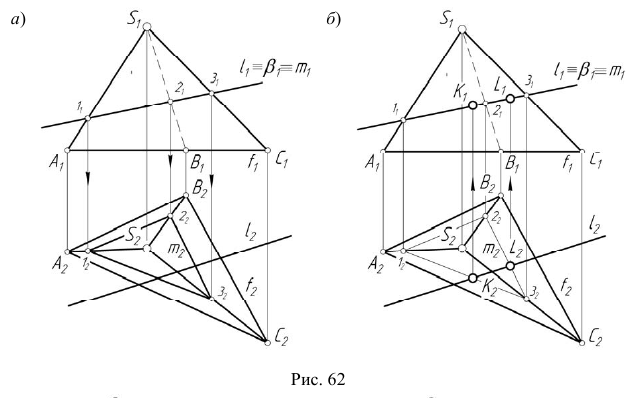
1. Заключим прямую линию 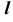во вспомогательную проецирующую плоскость 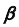(рис. 62, а).

Так как плоскость 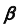— фронтально-проецирующая, то первая проекция линии 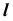совпадет с вырожденной проекцией плоскости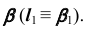

2. Строим линию пересечения m заданной поверхности 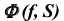и вспомогательной плоскости 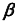в соответствии с алгоритмом решения задачи 8.

3. Определим точки пересечения K, L прямой линии 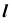с построенной линией m следующим образом (рис. 62, б):

• отметим проекции
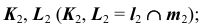
• на пересечении 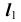и линий проекционной связи отметим проекции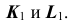

4. Определим видимость прямой 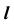относительно плоскости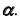

Невидимая часть прямой может находиться за поверхностью при проецировании на 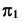и под поверхностью при проецировании на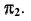

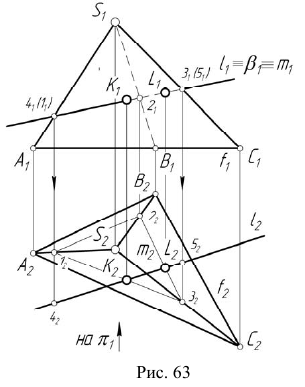
Для определения видимости прямой при проецировании на плоскость 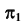используем конкурирующие точки 1 и 4, а также точки 3 и 5 (рис. 63). По расположению горизонтальных проекций 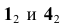можно сделать вывод, что точка 3, принадлежащая 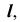— видимая. Следовательно, часть прямой от точки 4 до точки K — тоже видимая. На плоскости проекций 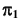этот участок прямой 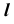отметим основной линией. На основании расположения горизонтальных проекций 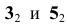можно сделать вывод, что точка 5, принадлежащая 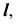— невидимая. Следовательно, часть прямой 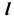от точки K до точки 5 находится за поверхностью. На плоскости проекций 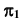этот участок прямой 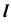отметим штриховой линией.

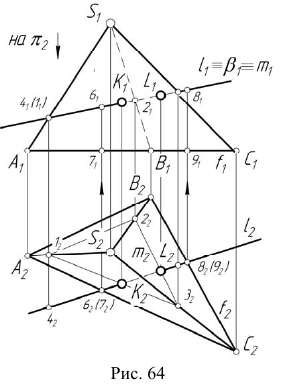
Для определения видимости прямой при проецировании на плоскость 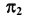используем конкурирующие точки 6 и 7, а также точки 8 и 9 (рис. 64). По расположению фронтальных проекций 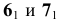можно сделать вывод, что точка 6, принадлежащая 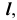— видимая. Следовательно, часть прямой 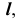содержащая точку 6, — тоже видимая. На плоскости проекций 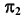этот участок прямой 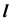отметим основной линией. Аналогично определим видимость участка прямой 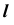, содержащего точку 8.