
Пересечение прямой линии с поверхностью с примерами
Пересечение прямой линии с поверхностью:
Для построения точки пересечения прямой с поверхностью через прямую следует провести вспомогательную плоскость и найти линию пересечения этой плоскости с поверхностью. Точка пересечения (или точка встречи заданной прямой и построенной линии или фигуры сечения) на поверхности и будет искомой точкой пересечения прямой с поверхностью. Сложность решения задачи зависит от трудоемкости нахождения линии пересечения, которая определяется следами поверхности и расположением прямой относительно как поверхности, так и плоскости проекций. Чтобы получить рациональное решение, следует пользоваться наиболее простым способом определения линии пересечения. Этого можно достичь двумя путями:
- выбором положения вспомогательной секущей плоскости;
- переводом секущей прямой в частное положение.
Вспомогательная секущая плоскость -проецирующая
Задание: определить точки пересечения прямой m с поверхностью пирамиды SABC (рис. 12.1).
Решение: для решения задачи прямую m заключают во фронтально проецирующую плоскость Σ (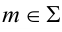
Задание: определить точки пересечения прямой m с поверхностью прямого кругового цилиндра (рис. 12.2).
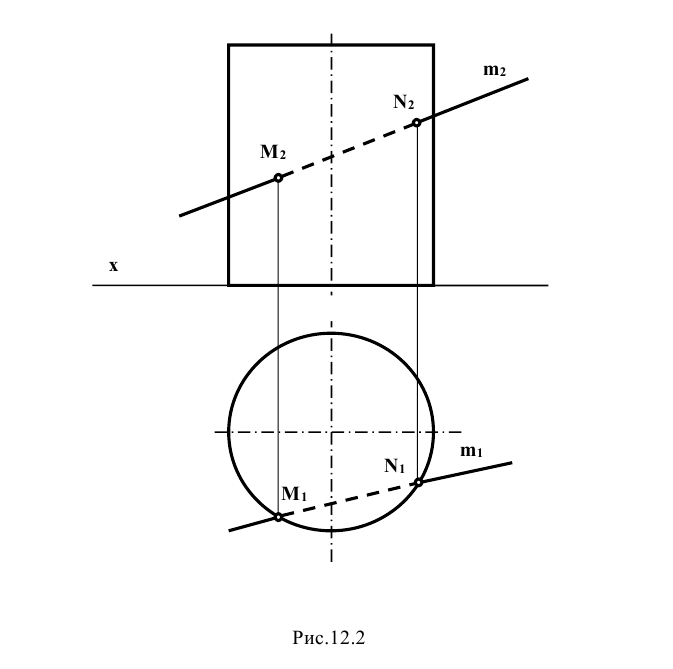
Решение: при решении задачи выделим проекции точек пересечения М и N прямой m с поверхностью цилиндра на горизонтальной проекции - точки 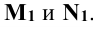 . Так как образующие прямого кругового цилиндра являются горизонтально проецирующими прямыми, фронтальные проекции точек пересечения прямой m с поверхностью цилиндра
. Так как образующие прямого кругового цилиндра являются горизонтально проецирующими прямыми, фронтальные проекции точек пересечения прямой m с поверхностью цилиндра 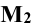 и
и 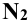 находят с помощью линий проекционной связи, как это показано на рисунке.
находят с помощью линий проекционной связи, как это показано на рисунке.
Вспомогательная секущая плоскость общего положения
Вспомогательную секущую плоскость, проводимую через прямую, при пересечении ею какой-либо поверхности, следует выбирать так, чтобы в результате получилось простейшее сечение. Например, при пересечении конической поверхности прямой линией такой плоскостью является плоскость, проходящая через вершину и пересекающая эту поверхность по прямым линиям (образующим).
При пересечении цилиндрической поверхности прямой линией вспомогательную плоскость целесообразно проводить через заданную прямую параллельно образующим цилиндра.
Задание: определить точки пересечения прямой m с поверхностью прямого кругового конуса (рис. 12.3).
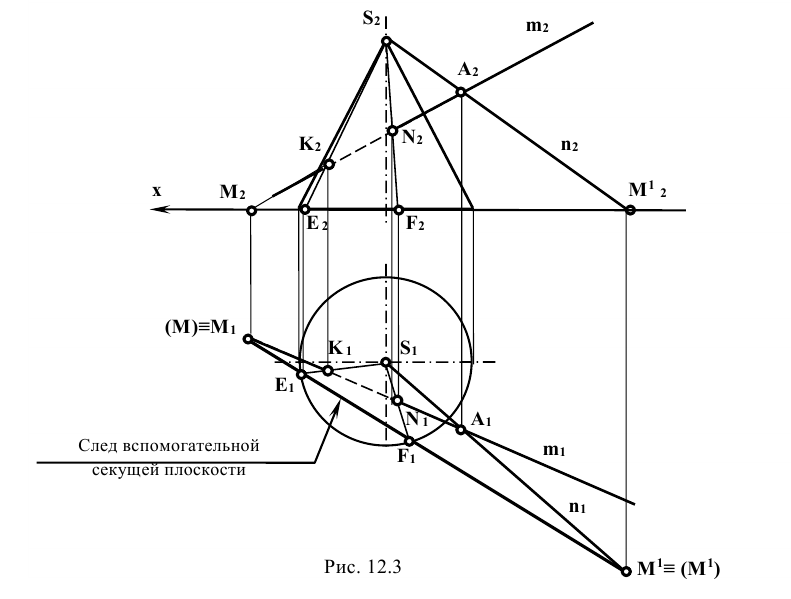
Решение: прямую m заключают в плоскость Р, проходящую через вершину конической поверхности S. Плоскость Р задана пересекающимися прямыми m и n, проходящими через точку А, которая выбирается произвольно на заданной прямой m.
Для определения горизонтального следа плоскости Р находят горизонтальные следы прямых m и n. Следы отмечают точками, например, 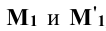 , в которых горизонтальный след
, в которых горизонтальный след 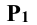 плоскости Р пересекает основание конической поверхности. Проекции
плоскости Р пересекает основание конической поверхности. Проекции 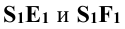 - образующие поверхности конуса, по которым она пересекается плоскостью Р.
- образующие поверхности конуса, по которым она пересекается плоскостью Р.
Точки 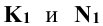 - горизонтальные проекции искомых точек пересечения. Зная положение
- горизонтальные проекции искомых точек пересечения. Зная положение 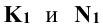 определяют фронтальные проекции
определяют фронтальные проекции 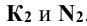 .
.
Перевод прямой общего положения, пересекающей заданную поверхность в частное положение
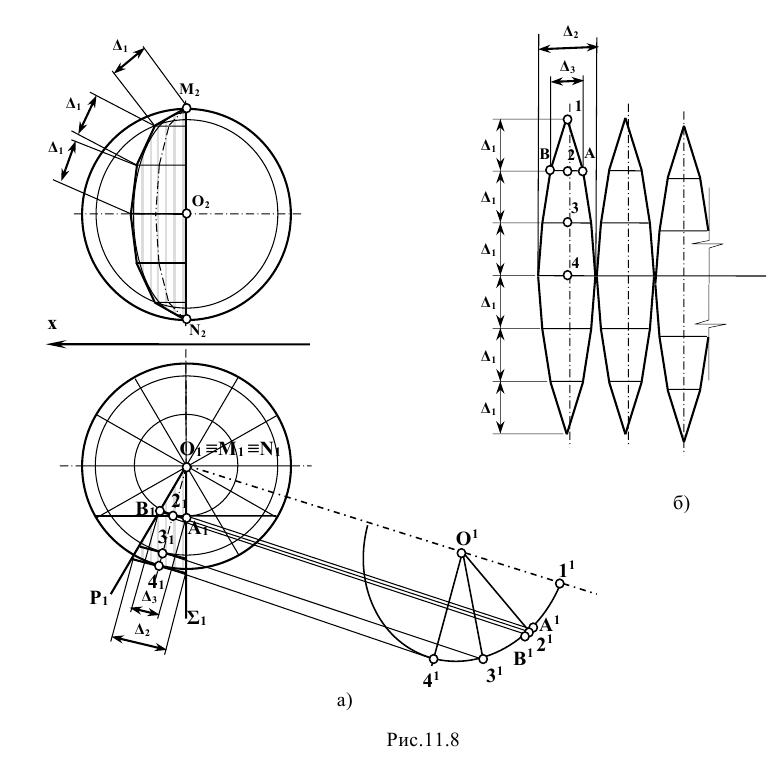
При пересечении поверхности сферы плоскостью в сечении получается окружность, которая проецируется на плоскости проекции в виде эллипсов или прямой и эллипса (если секущая плоскость - проецирующая). В случае, когда секущая плоскость параллельна плоскости проекции, окружность проецируется на эту плоскость проекции без искажения. Поэтому для упрощения решения задачи следует произвольно расположенную прямую перевести в положение, параллельное какой-либо плоскости проекции. Тогда прямую можно заключить в плоскость, параллельную плоскости проекции.
Задание: определить точки встречи прямой m, заданной отрезком АВ, с поверхностью сферы (рис. 12.4).
Решение: при решении этой задачи переводят прямую m общего положения в положение, параллельное плоскости проекции. Для этого вводят новую систему плоскостей 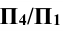 в которой
в которой 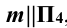 , и переходят от системы
, и переходят от системы 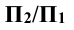 к системе
к системе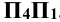 . Новую ось проекций
. Новую ось проекций 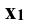 проводят параллельно горизонтальной проекции прямой
проводят параллельно горизонтальной проекции прямой 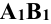 .
.
Далее от концов горизонтальной проекции прямой, точек 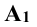 и
и 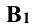 проводят линии проекционной связи, перпендикулярные к новой оси проекций, и на них на плоскости
проводят линии проекционной связи, перпендикулярные к новой оси проекций, и на них на плоскости 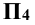 откладывают координаты
откладывают координаты 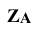 и
и 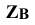 т.е. расстояния от оси проекций х до фронтальных проекций точек
т.е. расстояния от оси проекций х до фронтальных проекций точек 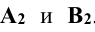 . Новая проекция
. Новая проекция 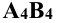 будет натуральной длиной отрезка прямой АВ.
будет натуральной длиной отрезка прямой АВ. 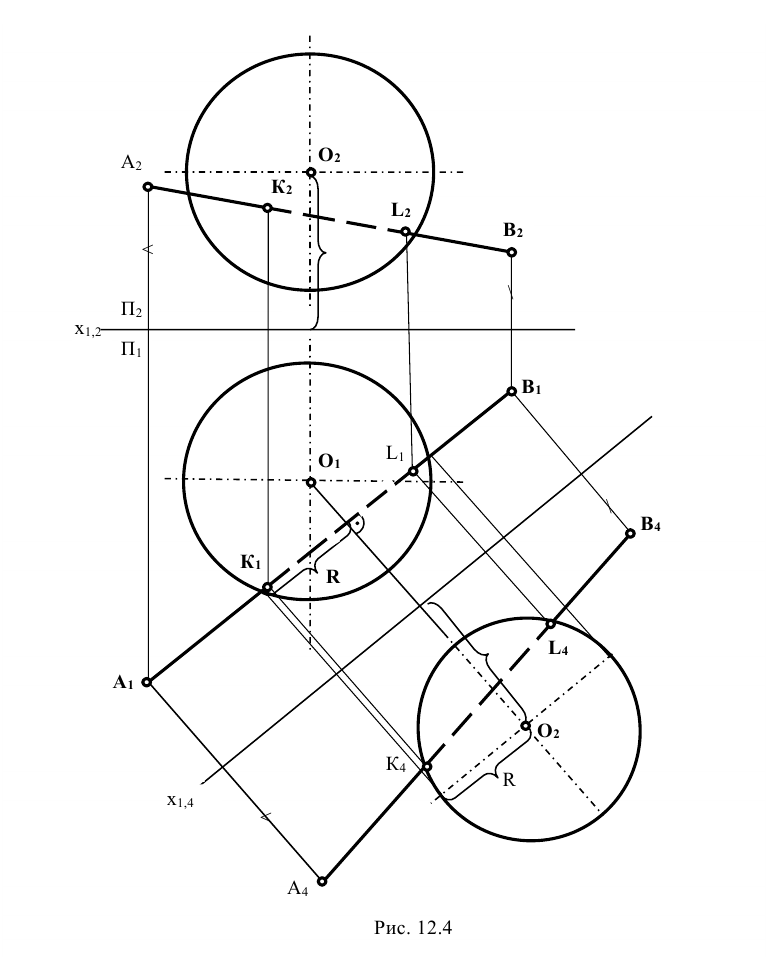
Аналогично находят и центр сферы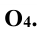
В новой системе горизонтально проецирующая плоскость Р 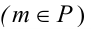 пересечет поверхность сферы по окружности радиусом R, которая спроецируется на плоскость
пересечет поверхность сферы по окружности радиусом R, которая спроецируется на плоскость 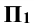 в отрезок (1-2), а на плоскость
в отрезок (1-2), а на плоскость 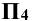 в окружность тем же радиусом R. Точки
в окружность тем же радиусом R. Точки 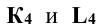 - вспомогательные проекции точек пересечения, по которым определяют проекции точек
- вспомогательные проекции точек пересечения, по которым определяют проекции точек 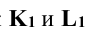 а затем
а затем 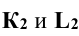 .
.
Плоскость, касательная к поверхности
Плоскость, касательная к поверхности в заданной на поверхности точке, есть множество всех прямых — касательных, проведенных к поверхности через заданную точку.
Для задания плоскости, касательной к поверхности в заданной точке, достаточно провести через эту точку две произвольные линии, принадлежащие поверхности (желательно простые по форме) и к каждой их них построить касательные в точке пересечения этих линий. Построенные прямые (касательные) определяют касательную плоскость.
Задание: построить плоскость Р, касательную к поверхности сферы и проходящую через точку К (рис. 12.5).
Решение: плоскость, касательная к сфере, перпендикулярна к радиусу, проведенному в точку касания. Поэтому, проведя радиус ОК, строят плоскость, задавая ее горизонталью КВ и фронталью КС. 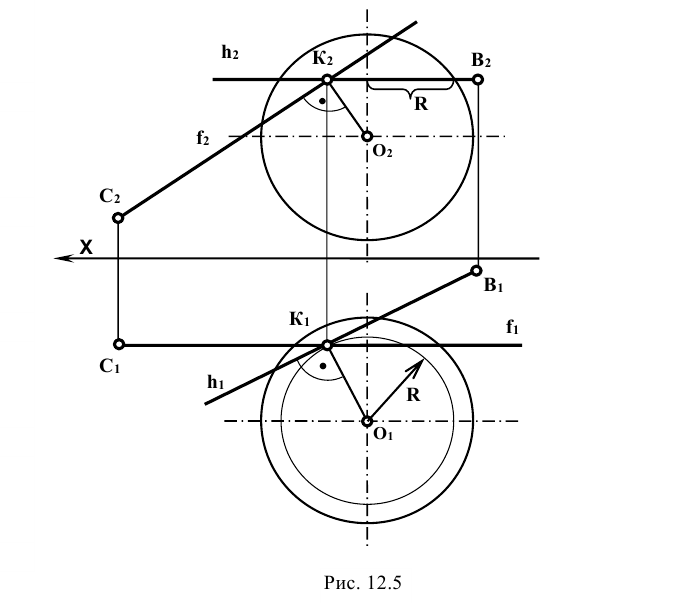
При этом горизонтальная проекция 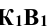 перпендикулярна к
перпендикулярна к 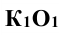 , а фронтальная проекция
, а фронтальная проекция 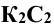 перпендикулярна к
перпендикулярна к 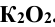 .
.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |