Пересечение поверхностей вращения плоскостью с примерами

Содержание:

Пересечение поверхностей вращения плоскостью:

Линия пересечения кривой поверхности с плоскостью представляет собой плоскую кривую, которая может распадаться и на прямые линии в случае пересечения плоскости с линейчатой поверхностью по ее образующим.

Для построения этой кривой линии на чертеже находят проекции ее отдельных точек, соединяемых с помощью лекала.

Среди точек линии пересечения имеются точки, которые занимают особое расположение на кривой или выделяются своим местоположением относительно плоскостей проекций. Такие точки называют опорными или характерными. К ним относятся высшие и низшие, ближние и дальние, точки, расположенные на крайних образующих (точки видимости) и др.

Остальные точки называются промежуточными или случайными.

Для нахождения точек линии пересечения применяются вспомогательные секущие плоскости (проецирующие или плоскости уровня).

Вспомогательные плоскости выбираются так, чтобы в пересечении с кривой поверхностью получались простейшие линии - прямые и окружности.

Пересечение цилиндра плоскостью

При пересечении цилиндра вращения плоскостью возможны случаи:

• секущая плоскость параллельна оси - в сечении цилиндрической поверхности полу-чаются две прямые (образующие) (рис. 8.1а);
• секущая плоскость перпендикулярна оси - в сечении получается окружность, равная окружностям оснований (рис. 8.1б);
• секущая плоскость наклонна к оси - в сечении получается эллипс, малая ось которого всегда равна диаметру цилиндра, а большая зависит от угла ϕ (рис. 8.1в).

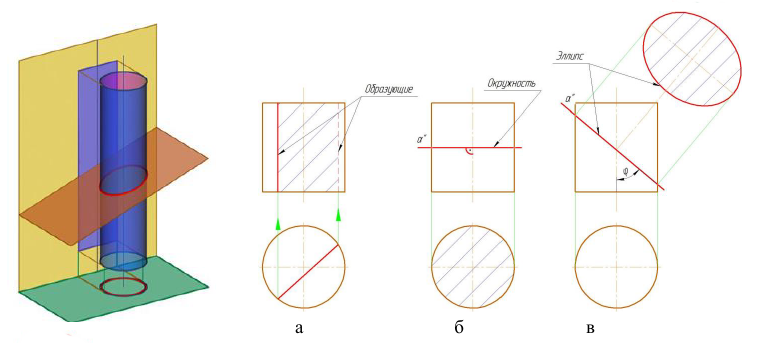
Рисунок 8.1 - Пересечение цилиндра плоскостью

Горизонтальная плоскость Р (Р") пересекает поверхность цилиндра по части окружности, профильная плоскость T (T") по прямым АВ и CD (образующим цилиндра), фронтально-проецирующая плоскость Q (Q") - по части эллипса [5]. Фронтальная проекция линий пересечения совпадает со следами - проекциями секущих плоскостей (P ", T ", Q"), а горизонтальная — с окружностью оснований цилиндра (рис. 8.2).

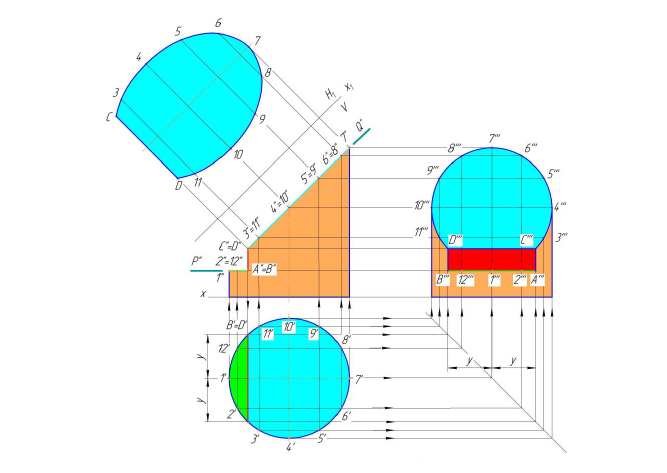
Рисунок 8.2 - Построение проекций усеченной части цилиндра

Построение профильной проекции сводится к построению профильных проекций точек по двум заданным, направление построений линий связи указано стрелками). Вместо ломаных линий связи при построении профильных проекций точек можно использовать координаты y , которые откладываются на горизонтальных линиях связи по разные стороны оси цилиндра (см. построение точек А, В, С, D).

Обычно для построения точек линий сечения пользуются образующими, равноотстоящими друг от друга. Поэтому горизонтальная проекция цилиндра (окружность) разделена на 12 частей (точки 1, 2... 12). Этой равномерной «разметкой» удобно пользоваться не только для построения проекций сечений, но и для построения развертки.

Действительный вид фигуры сечения плоскостью Q построен способом перемены плоскостей проекций. Новая ось проекций х1 проведена параллельно следу - проекции Q". Выполнив соответствующие построения на плоскости H1, получим натуральную величину сечения цилиндра плоскостью Q.

Пересечение конуса плоскостью

В зависимости от положения секущей плоскости линиями сечения конической поверхности (рис. 8.3) могут быть: эллипс, парабола, гипербола, а в частных случаях: окружность, прямая, две пересекающиеся прямые и точка.

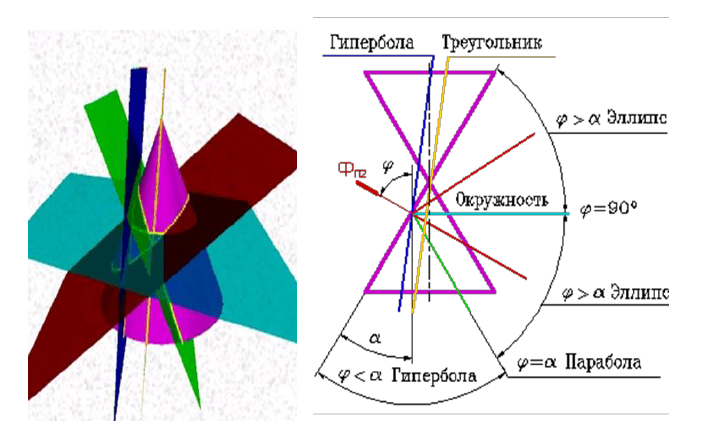
Рисунок 8.3 - Пересечение конуса плоскостью

Если плоскость Ф пересекает все образующие поверхности конуса вращения, т.е. если φ>α, то линией сечения является эллипс. В этом случае секущая плоскость не параллельна ни одной из образующих поверхности конуса.

В частном случае (φ=90) такая плоскость пересекает поверхность конуса по окружности; и сечение вырождается в точку, если плоскость проходит через вершину конуса.

Если плоскость Ф параллельна одной образующей поверхности конуса, т.е. φ=α, то линией пересечения является парабола. В частном случае (плоскость является касательной к поверхности конуса) сечение вырождается в прямую.

Если плоскость Ф параллельна двум образующим поверхности конуса (в частном случае параллельна оси конуса), т.е. φ<α, то линией сечения является гипербола. В случае прохождения плоскости через вершину конической поверхности фигурой сечения могут быть сами образующие, т.е. гипербола вырождается в две пересекающие прямые.

При пересечении конуса вращения получаются различные виды кривых второго порядка (конические сечения) [5]. Рассмотрим возможные случаи пе-ресечения конуса фронтально-проецирующими плоскостями (угол между сле дом - проекцией и осью конуса - α , половина угла конуса при вершине –S.

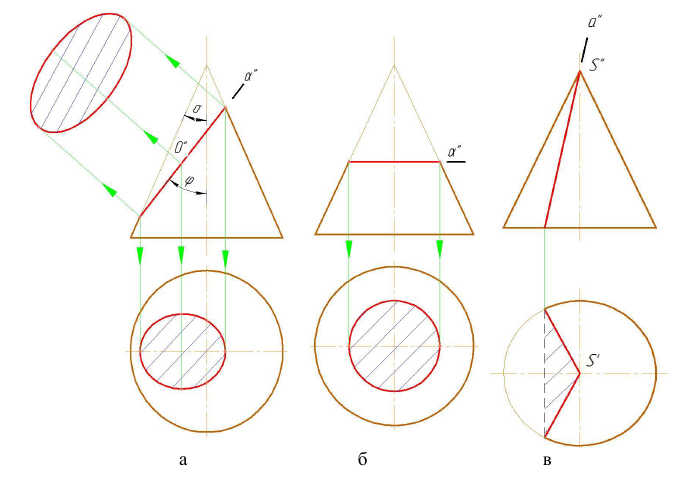
Рисунок 8.4 - Конические сечения

Секущая плоскость α (α") пересекает все образующие конуса ( не парал-лельные ни одной из образующих конуса) - в сечении получается эллипс ( φ> δ) (рис. 8.4 а).

В частности, если секущая плоскость перпендикулярна оси конуса, то получается окружность (рис. 8.4 б).

В частном случае, если секущая плоскость проходит через вершину конуса, то в сечении получается пара пересекающихся в вершине прямых (образующих) (рис. 8.4 в).

Секущая плоскость α (α") параллельная одной образующей конуса в сечении получается парабола (φ = φ) (рис. 8.5 а).

Секущая плоскость α1 (α1") параллельна двум образующим конуса- в се-чении получается гипербола (φ < δ) (рис. 8.6 б). Профильная плоскость α2 (α2") образует с осью конуса угол равный 0, что не противоречит вышеуказанному неравенству.

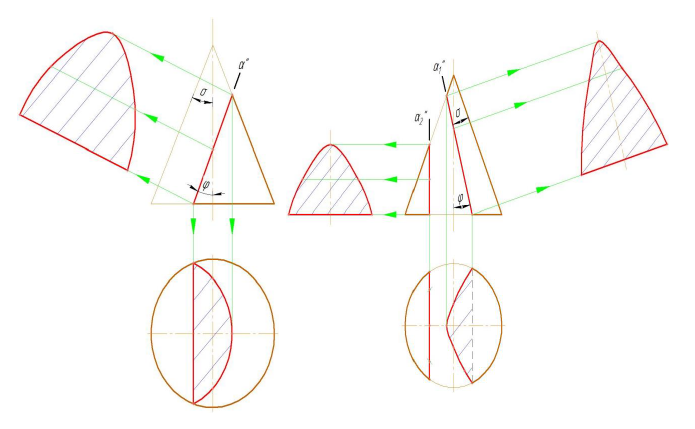
Рисунок 8.6 - Конические сечения

Если конус вращения пересекается плоскостью общего положения, то о линии пересечения можно судить, преобразовав плоскостью общего положения в проецирующую. Преобразование рационально выполнить переменой плоскостей проекций.

На рис. 8.7 показано построение проекций усеченной части конуса вращения плоскостями частного положения α и β.

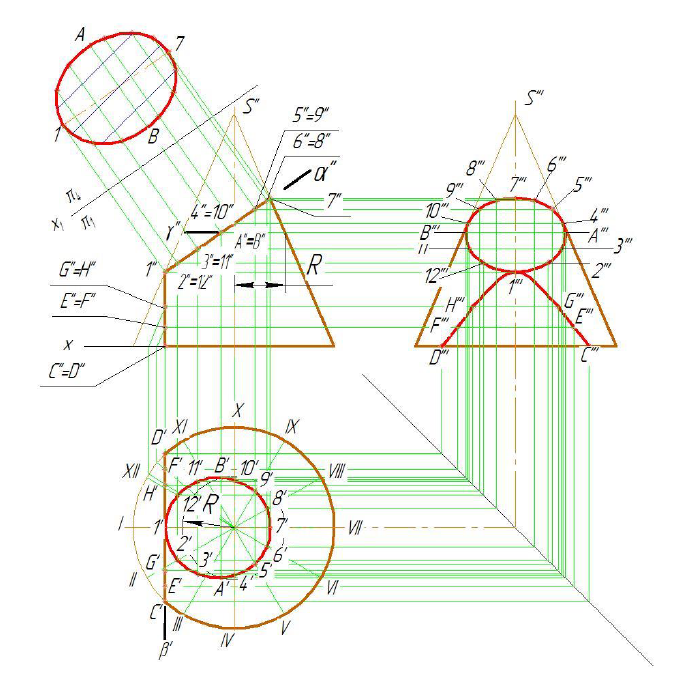
Рисунок 8.7 - Построение проекций усеченной части конуса

• Заказать чертежи

Пересечение сферы и тора плоскостью

При пересечении сферы плоскостью всегда получается окружность, которая в зависимости от положения секущей плоскости по отношению к плоскостям проекций, проецируется в виде прямой, в виде эллипса или в виде окружности.

В зависимости от положения плоскости по отношению к плоскостям проекций, сложность решения позиционной задачи, по определению линии пересечения ее с поверхностью существенно меняется. Наиболее простым представляется случай, когда плоскость проецирующая. Рассмотрим решение задачи по определению линии пересечения сферы фронтально - проецирующей плоскостью.

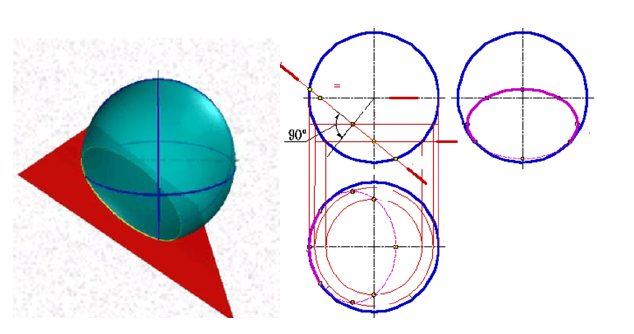
Рисунок 8.8 - Пересечение сферы плоскостью

На рис. 8.9 показано построение проекций усеченной сферы плоско-стями частного положения S, P, Q [5]. Фронтальная проекция линий пересе-чения совпадает со следами - проекциями секущих плоскостей (S, P, Q ).

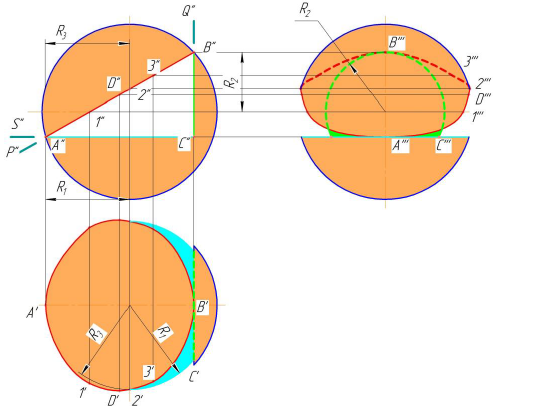
Рисунок 8.9 - Построение проекций сечения сферы плоскостями

Горизонтальная проекция сечения сферы плоскостью S - окружность радиуса R1, а профильная — прямая.

Профильная проекция сечения плоскостью Q - окружность радиуса R2, а горизонтальная - прямая.

Плоскость P пересекает сферу по окружности, которая на плоскости Н и W проецируется в виде эллипса. Две вершины этого эллипса (точки А и В) являются низшей и высшей точками сечения. Точки 1 и 2, лежащие на экваторе и профильном меридиане, определяют видимые части горизонтальной и профильной проекций от невидимой (точки обозначены только на одной симметричной части сечения). Вершина эллипса D (конец большой оси) определена при помощи горизонтальной секущей плоскости.

Дополнительная секущая плоскость пересекает заданную плоскость Р на фронтально проецирующей прямой, а сферу - по окружности радиуса R, проецирующейся на плоскость Н в натуральную величину. Профильная проекция D'" точки D строится по линиям связи. Аналогичным способом находят промежуточные точки 3, используя следующую вспомогательную секущую плоскость.

Видимость горизонтальной и профильной проекций линий сечений определяется в зависимости от расположения их относительно экватора и профильного меридиана сферы.

При пересечении тора плоскость в общем случае получается кривая 4-го порядка, в частных случаях она может распадаться на две кривые 2-го порядка.

На рис. 8.9 показано построение проекций усеченной части открытого тора фронтально-проецирующей плоскостью Q (Qꞌꞌ).

Фронтальная проекция линии пересечения совпадает со следом – проекцией секущей плоскостью α.

Для построения кривой пересечения определены точки А, В, С, D, E и промежуточные 1, 2, 3, 4.

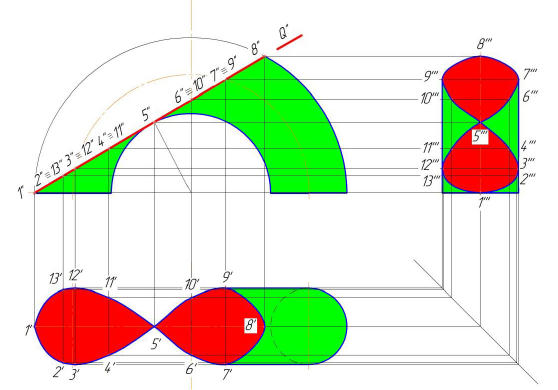
Рисунок 8.9 - Построение проекций сечения тора плоскостью

Точки А и В лежат на экваторе (наибольшей параллели) тора, точка С на горле (наименьшей параллели). Точка D и Е лежат на крайних параллелях (точки обозначены только на одной симметричной части сечения).

Промежуточные точки 1 и 2 расположены на параллелях m , точки 3.4 – на параллелях n. Построение горизонтальных проекций показано стрелками.

Профильные проекции точек кривой пересечения построены при помощи линий связи