
Пересечение поверхностей в начертательной геометрии с примерами
Содержание:
Пересечение поверхностей:
В этом разделе рассмотрим решение задач по определению линии пересечения:
- плоскостей как простейших видов поверхностей;
- плоскости с поверхностью;
- поверхностей.
В зависимости от формы поверхностей, их взаимного положения и положения относительно плоскостей проекций используются различные способы построения их линии пересечения [3], [7].
В данном пособии рассмотрим следующие способы построения линии пересечения поверхностей:
- Алгоритм построения линии, принадлежащей поверхности (плоскости). Этот способ используется, когда одна из двух заданных поверхностей — проецирующая.
- Способ вспомогательных секущих плоскостей. Этот способ рационально применять тогда, когда есть возможность пересечь обе поверхности плоскостью по графически простым линиям (прямым, окружностям).
- Способ вспомогательных концентрических сфер. Этот способ применяется для определения линии пересечения поверхностей вращения, оси вращения которых пересекаются.
Пересечение плоскостей
Способ вспомогательных секущих плоскостей Для построения линии пересечения плоскостей общего положения используется способ вспомогательных секущих плоскостей.
Рассмотрим общий алгоритм решения задачи по определению линии пересечения поверхностей (плоскостей) способом секущих плоскостей.
Задача:
Построить линию пересечения 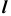
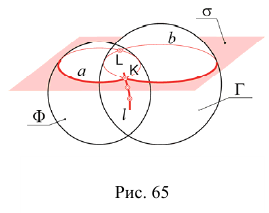
Алгоритм решения
- Рассечем обе поверхности вспомогательной плоскостью
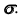
- Определим линию пересечения
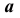 плоскости
плоскости 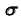 с поверхностью
с поверхностью 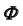
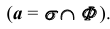
- Определим линию пересечения
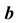 плоскости
плоскости  с поверхностью
с поверхностью 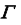
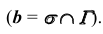
- Построим точки пересечения линий
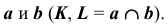
Для построения других точек искомой линии повторим указанный алгоритм необходимое количество раз.
При решении задачи на пересечение плоскостей линии a и b представляют собой прямые линии, а рассмотренный алгоритм построения общих точек пересекающихся поверхностей применяется дважды.
Задача:
На эпюре Монжа построить линию пересечения 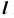 плоскости
плоскости 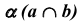 с плоскостью
с плоскостью 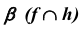 (рис. 66).
(рис. 66).
Решим эту задачу в соответствии с алгоритмом решения задачи 10. В качестве вспомогательных секущих плоскостей будем использовать, например, плоскости уровня 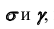 параллельные
параллельные 
Алгоритм решения
1. Рассечем обе плоскости вспомогательной плоскостью 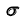 (см. рис. 66, а).
(см. рис. 66, а).
2. Определим линию пересечения 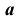 плоскости
плоскости 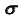 с плоскостью
с плоскостью 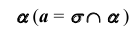 в соответствии с алгоритмом решения задачи 6.
в соответствии с алгоритмом решения задачи 6.
3. Определим линию пересечения 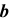 плоскости
плоскости 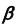 с плоскостью
с плоскостью 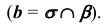
4. Определим проекции одной общей точки заданных плоскостей — точки 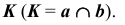
5. Рассечем обе плоскости вспомогательной плоскостью 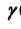 (см. рис. 66, б).
(см. рис. 66, б).
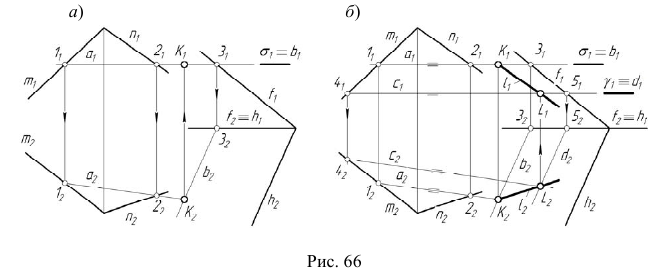
6. Определим линию пересечения c плоскости 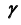 с плоскостью
с плоскостью 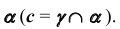 7. Определим линию пересечения
7. Определим линию пересечения 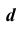 плоскости
плоскости 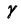 с плоскостью
с плоскостью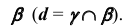
8. Определим проекции еще одной общей точки заданных плоскостей — точки 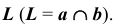
9. Построим проекции искомой прямой линии, соединив соответствующие проекции точек K и L.
Пересечение плоскости общего положения с проецирующей поверхностью
Для определения линии пересечения плоскости общего положения с проецирующей поверхностью будем использовать собирательное свойство вырожденной проекции проецирующей поверхности и применять алгоритм построения линии, принадлежащей заданной плоскости.
Задача:
На эпюре Монжа построить проекции линии пересечения 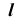 призматической проецирующей поверхности
призматической проецирующей поверхности 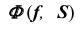 с плоскостью
с плоскостью 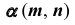 (рис. 67, а).
(рис. 67, а).
Алгоритм решения
1. Так как призматическая поверхность 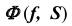 — горизонтально- проецирующая, то вторая проекция линии пересечения поверхности с плоскостью совпадает с вырожденной горизонтальной проекцией поверхности
— горизонтально- проецирующая, то вторая проекция линии пересечения поверхности с плоскостью совпадает с вырожденной горизонтальной проекцией поверхности  (рис. 67, б).
(рис. 67, б).
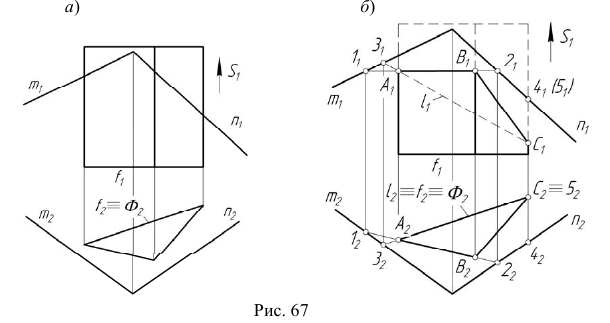
Отметим горизонтальную проекцию 
2. Фронтальную проекцию  определим по принадлежности линии
определим по принадлежности линии 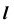 плоскости
плоскости 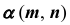 (рис. 67, б).
(рис. 67, б).
Пересечение плоскости общего положения с поверхностью общего положения
В этом разделе рассмотрим задачу, при решении которой используется способ секущих плоскостей.
Задача:
На эпюре Монжа построить проекции линии пересечения 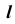 поверхности
поверхности 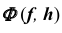 с плоскостью
с плоскостью 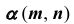 (см. рис. 68, а).
(см. рис. 68, а).
Для решения этой задачи в качестве вспомогательных плоскостей используем плоскости уровня, так как одна из проекций линии пересечения такой плоскости со сферой представляет собой прямую, а вторая — окружность.
Алгоритм решения
1. Определим проекции точек изменения видимости линии 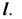
а) Строим проекции точек A и B, используя в качестве вспомогательной плоскости — плоскость 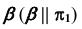 (рис. 68, б):
(рис. 68, б):
- определим проекции линии пересечения плоскости
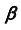 со сферой
со сферой 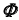 — окружность
— окружность 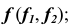
- определим проекции линии пересечения плоскости
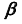 с плоскостью
с плоскостью 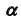 в соответствии с алгоритмом решения задачи 6 — прямая
в соответствии с алгоритмом решения задачи 6 — прямая 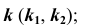
- отметим проекции точек
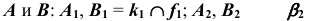
б) Строим проекции точек С и D, используя в качестве вспомогательной плоскости плоскость уровня 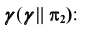
- определим проекции линии пересечения плоскости
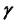 со сферой — окружность
со сферой — окружность 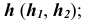
- определим проекции линии пересечения плоскости
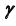 с плоскостью
с плоскостью 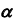 — прямая
— прямая 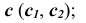
- отметим проекции точек
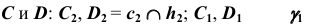
2. В соответствии с алгоритмом решения задачи 10 определим произвольные общие точки 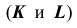 заданных фигур, используя в качестве вспомогательной плоскости плоскость уровня
заданных фигур, используя в качестве вспомогательной плоскости плоскость уровня 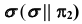 (рис. 68, в):
(рис. 68, в):
- определим проекции линии пересечения плоскости
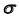 со сферой в соответствии с алгоритмом решения задачи 8 – окружность
со сферой в соответствии с алгоритмом решения задачи 8 – окружность 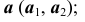
- определим проекции линии пересечения плоскости
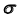 с плоскостью
с плоскостью 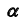 в соответствии с алгоритмом решения задачи 6 – прямая
в соответствии с алгоритмом решения задачи 6 – прямая 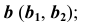
- отметим проекции точек
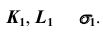
- Для построения других точек искомой линии
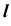 повторим последовательность построений пункта 2 данной задачи.
повторим последовательность построений пункта 2 данной задачи.
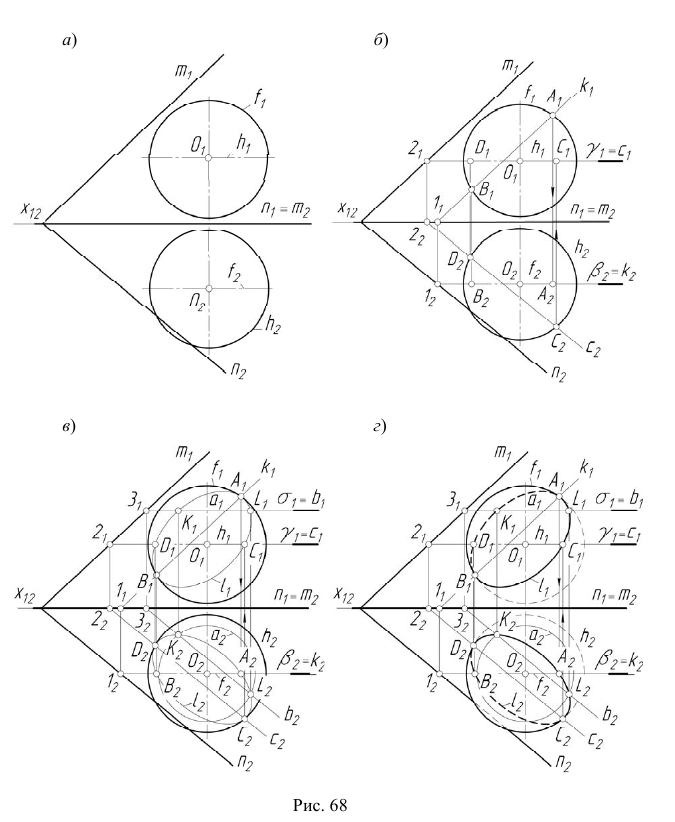
3. Определим видимость линии 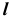 (рис. 68, г), используя точку K. При проецировании на плоскость
(рис. 68, г), используя точку K. При проецировании на плоскость 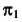 точка K принадлежит невидимой части сферы, следовательно, часть линии
точка K принадлежит невидимой части сферы, следовательно, часть линии 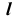 от точки A до точки B, содержащая точку K, — невидимая. В поле проекций
от точки A до точки B, содержащая точку K, — невидимая. В поле проекций 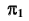 этот участок
этот участок 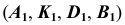 отметим штриховой линией.
отметим штриховой линией.
При проецировании на плоскость 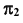 точка K принадлежит видимой части сферы, следовательно, часть линии
точка K принадлежит видимой части сферы, следовательно, часть линии 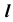 от точки C до точки D, содержащая точку K, — видимая. В поле проекций
от точки C до точки D, содержащая точку K, — видимая. В поле проекций 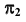 этот участок
этот участок 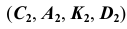 отметим сплошной основной линией.
отметим сплошной основной линией.
Пересечение проецирующей поверхности с поверхностью общего положения
Для определения линии пересечения проецирующей поверхности с поверхностью общего положения будем использовать собирательное свойство вырожденной проекции проецирующей поверхности и применять алгоритм построения линии, принадлежащей поверхности общего положения.
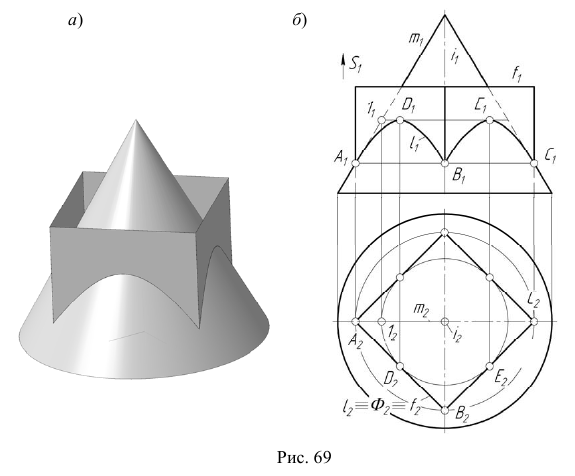
Задача:
На эпюре Монжа построить проекции линии пересечения 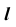 проецирующей призматической поверхности
проецирующей призматической поверхности 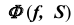 с поверхностью общего положения
с поверхностью общего положения 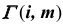 (рис. 69, а).
(рис. 69, а).
Алгоритм решения
- Так как призматическая поверхность
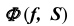 — горизонтально-проецирующая, то вторая проекция линии пересечения поверхностей совпадает с вырожденной горизонтальной проекцией поверхности
— горизонтально-проецирующая, то вторая проекция линии пересечения поверхностей совпадает с вырожденной горизонтальной проекцией поверхности 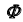 (рис. 69, б).
(рис. 69, б). - Отметим горизонтальную проекцию
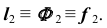
- Фронтальную проекцию
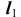 определим по принадлежности линии
определим по принадлежности линии 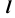 поверхности
поверхности 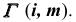
Проецирующие плоскости (грани призматической поверхности) пересекают коническую поверхность по гиперболическим кривым, фронтальными проекциями которых также будут гиперболические кривые.
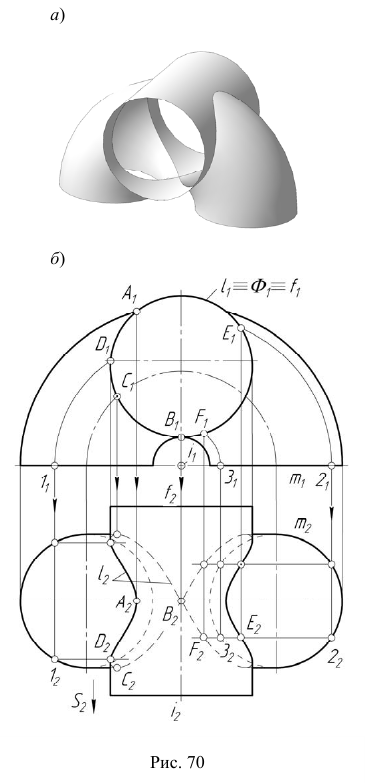
Задача:
На эпюре Монжа построить проекции линии пересечения  проецирующей цилиндрической поверхности
проецирующей цилиндрической поверхности 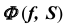 с торовой поверхностью
с торовой поверхностью 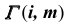 (рис. 70, а).
(рис. 70, а).
Вначале определим характер линии пересечения этих поверхностей и ее проекций.
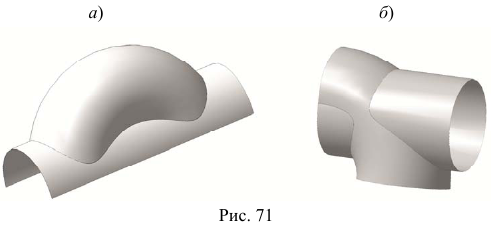
На основании теоремы о пересечении алгебраических поверхностей порядков n и m [3] цилиндрическая поверхность второго порядка пересекается с торовой поверхностью четвертого порядка в общем случае по пространственной кривой восьмого порядка (2·4=8) (рис. 71, а). При частном взаимном расположении поверхностей линия их пересечения может распадаться на две или более составляющих кривых меньших порядков (рис. 71, б).
В данной задаче линией пересечения являются две кривые четвертого порядка.
Алгоритм решения
1. Так как поверхность 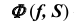 — фронтально-проецирующая то первая проекция линии пересечения поверхностей совпадает с вырожденной фронтальной проекцией цилиндрической поверхности
— фронтально-проецирующая то первая проекция линии пересечения поверхностей совпадает с вырожденной фронтальной проекцией цилиндрической поверхности  (рис. 70, б).
(рис. 70, б).
Отметим фронтальную проекцию 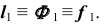
2. Горизонтальную проекцию  определим по принадлежности линии
определим по принадлежности линии  поверхности тора
поверхности тора 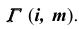 Горизонтальная проекция линии
Горизонтальная проекция линии 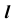 представляет собой две кривые четвертого порядка.
представляет собой две кривые четвертого порядка.
3. Определение видимости.
При проецировании на плоскость 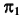 видимая и невидимая части линии
видимая и невидимая части линии 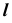 совпадают. Видимость при проецировании на горизонтальную плоскость проекций ограничивает цилиндр. Поэтому видимость линии при проецировании на плоскость проекций
совпадают. Видимость при проецировании на горизонтальную плоскость проекций ограничивает цилиндр. Поэтому видимость линии при проецировании на плоскость проекций 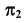 определится, например, положением точки A. Точка A при- надлежит видимой части цилиндра, следовательно, часть линии
определится, например, положением точки A. Точка A при- надлежит видимой части цилиндра, следовательно, часть линии 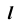 от точки A до контурной линии цилиндрической поверхности — видимая. В поле проекций
от точки A до контурной линии цилиндрической поверхности — видимая. В поле проекций 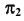 этот участок отмечен сплошной основной линией.
этот участок отмечен сплошной основной линией.
Пересечение поверхностей общего положения. Способ вспомогательных концентрических сфер
В качестве первого примера рассмотрим решение задачи на основе способа секущих плоскостей.
Задача:
На эпюре Монжа построить проекции линии пересечения конической поверхности 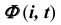 со сферой
со сферой 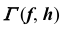 (рис. 72).
(рис. 72).
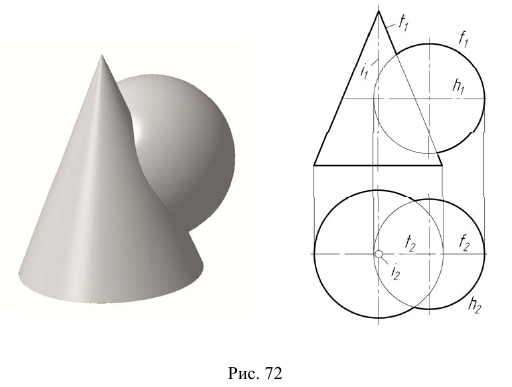
Вначале определим характер линии пересечения этих поверхностей и ее проекций. Две поверхности второго порядка пересекаются в общем случае по кривой четвертого порядка. Горизонтальная проекция искомой линии 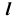 будет представлять собой кривую четвертого порядка. Фронтальная же проекция будет являться кривой второго порядка на основании следующей теоремы: если две поверхности порядка n и m имеют общую плоскость симметрии, то линия их пересечения прямоугольно проецируется на эту плоскость или ей параллельную в кривую порядка (n×m)/2.
будет представлять собой кривую четвертого порядка. Фронтальная же проекция будет являться кривой второго порядка на основании следующей теоремы: если две поверхности порядка n и m имеют общую плоскость симметрии, то линия их пересечения прямоугольно проецируется на эту плоскость или ей параллельную в кривую порядка (n×m)/2.
Для решения этой задачи в качестве вспомогательных плоскостей используются плоскости уровня, параллельные 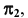 так как одна из проекций линии пересечения такой плоскости с заданными поверхностями представляет собой прямую, а вторая — окружность.
так как одна из проекций линии пересечения такой плоскости с заданными поверхностями представляет собой прямую, а вторая — окружность.
Алгоритм решения
1. Определим проекции точек изменения видимости линии  (рис. 73, а).
(рис. 73, а).
а) Строим проекции точек A и B, используя в качестве вспомогательной плоскость 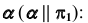
- определим проекции линии пересечения плоскости
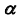 со сферой — окружность
со сферой — окружность 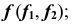
- определим проекции линии пересечения плоскости
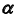 с конической поверхностью вращения — прямая
с конической поверхностью вращения — прямая 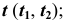
- отметим проекции точек
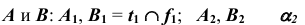
б) Строим проекции точек С и D, используя в качестве вспомогательной плоскости плоскость уровня 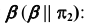
- определим проекции линии пересечения плоскости
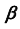 со сферой — окружность
со сферой — окружность 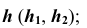
- определим проекции линии пересечения плоскости
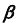 с конической поверхностью вращения — окружность
с конической поверхностью вращения — окружность 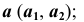
- отметим проекции точек
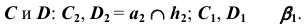
2. Определим произвольные общие точки (K и L) заданных фигур, используя в качестве вспомогательной плоскости плоскость уровня 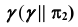 (рис. 73, б):
(рис. 73, б):
- - определим проекции линии пересечения плоскости
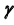 с конической поверхностью вращения — окружность
с конической поверхностью вращения — окружность 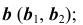
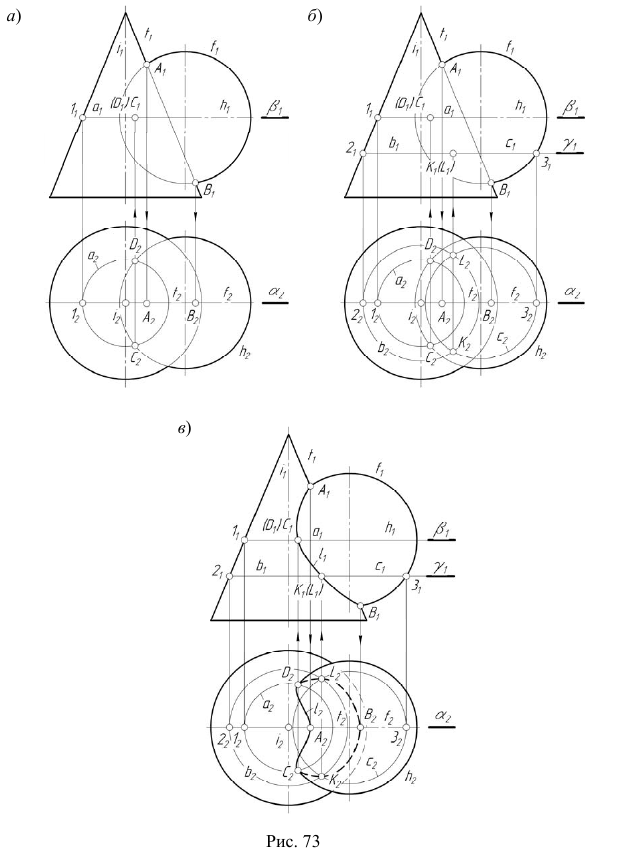
- - определим проекции линии пересечения плоскости
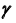 со сферой — окружность
со сферой — окружность 
- - отметим проекции точек
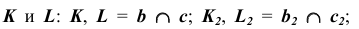
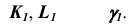
Для построения других точек искомой линии  повторим последовательность построений п. 2 данной задачи.
повторим последовательность построений п. 2 данной задачи.
3. Определим видимость линии 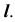
При проецировании на плоскость 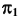 видимая и невидимая части линии
видимая и невидимая части линии 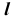 совпадают, так как общая плоскость симметрии поверхностей параллельна фронтальной плоскости проекций.
совпадают, так как общая плоскость симметрии поверхностей параллельна фронтальной плоскости проекций.
Видимость при проецировании на горизонтальную плоскость проекций ограничивает сфера. Поэтому видимость линии на 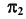 определится, например, положением точки A. Точка A принадлежит видимой части сферы, следовательно, часть линии
определится, например, положением точки A. Точка A принадлежит видимой части сферы, следовательно, часть линии 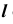 от точки C до точки D, содержащая точку A, — видимая. В поле проекций
от точки C до точки D, содержащая точку A, — видимая. В поле проекций 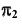 этот участок
этот участок 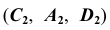 отмечен сплошной основной линией (рис. 73, в).
отмечен сплошной основной линией (рис. 73, в).
В качестве второго примера рассмотрим решение задачи на основе способа вспомогательных концентрических сфер.
Способ вспомогательных концентрических сфер
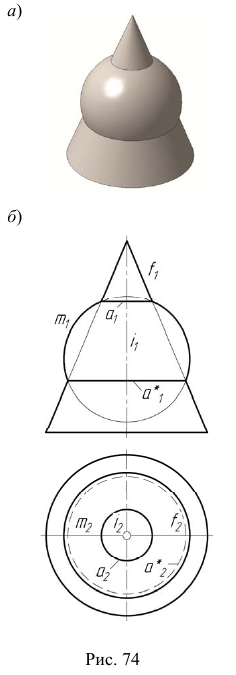
Способ вспомогательных концентрических сфер основан на следующем определении: две соосные поверхности вращения пересекаются по окружностям, плоскости которых перпендикулярны оси вращения 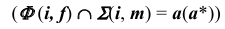 (рис. 74, а).
(рис. 74, а).
Этот способ применяется только для определения линии пересечения поверхностей вращения, оси вращения которых пересекаются, а общая плоскость симметрии должна быть плоскостью уровня. В этом случае вспомогательные сферы с центрами в точке пересечения осей вращения заданных поверхностей пересекают обе поверхности по окружностям, которые проецируются в виде прямых на плоскость, параллельную общей плоскости симметрии (рис. 74, б).
Задача:
На эпюре Монжа построить проекции линии пересечения 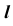 поверхности
поверхности 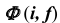 с поверхностью
с поверхностью 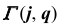 (рис. 75, а).
(рис. 75, а).
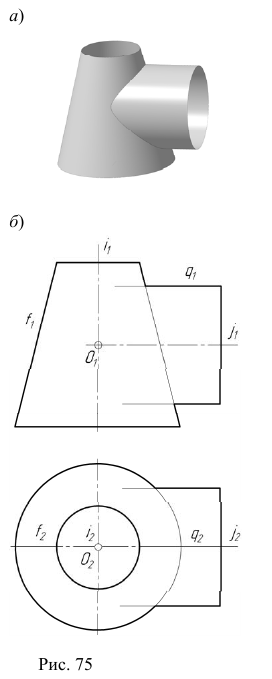
Вначале определим характер линии пересечения этих поверхностей и ее проекций. Две поверхности второго порядка пересекаются в общем случае по кривой четвертого порядка, поэтому горизонтальная проекция искомой линии 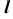 будет представлять собой кривую четвертого порядка. Фронтальная же проекция будет представлять собой кривую второго по- рядка, так как поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций.
будет представлять собой кривую четвертого порядка. Фронтальная же проекция будет представлять собой кривую второго по- рядка, так как поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций.
Для определения общих точек поверхностей будем пересекать их сферами с центрами в точке пересечения осей вращения этих поверхностей 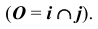
Алгоритм решения
Общая плоскость симметрии заданных поверхностей параллельна фронтальной плоскости проекций (рис. 75, б), поэтому решение задачи начнем с построения фронтальных очерков вспомогательных сфер.
1. Строим фронтальный очерк сферы наименьшего радиуса. Сферой наименьшего радиуса 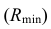 является сфера, касательная к одной из поверхностей и пересекающая другую. На эпюре Монжа этой сфере соответствует окружность, касательная очерковых прямых конической поверхности (рис. 76).
является сфера, касательная к одной из поверхностей и пересекающая другую. На эпюре Монжа этой сфере соответствует окружность, касательная очерковых прямых конической поверхности (рис. 76).
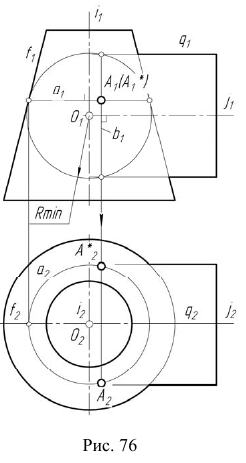
Сфера касается конической поверхности по окружности 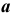 и пересекает цилиндрическую поверхность по окружности b. При этом плоскости окружностей а и b перпендикулярны осям вращения i и j соответственно.
и пересекает цилиндрическую поверхность по окружности b. При этом плоскости окружностей а и b перпендикулярны осям вращения i и j соответственно.
Первая пара общих точек поверхностей определится на пересечении этих окружностей — 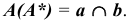 Фронтальные проекции общих точек определятся на пересечении отрезков прямых —
Фронтальные проекции общих точек определятся на пересечении отрезков прямых — 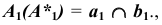 а горизонтальные проекции — по условию принадлежности конической поверхности, т.е.
а горизонтальные проекции — по условию принадлежности конической поверхности, т.е. 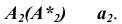
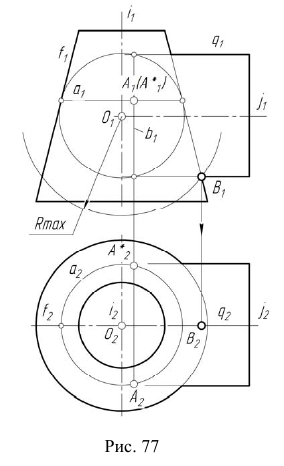
2. Строим фронтальный очерк сферы наибольшего радиуса. Радиусу наибольшей сферы 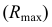 на фронтальной проекции соответствует расстояние от точки
на фронтальной проекции соответствует расстояние от точки 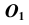 до наиболее удаленной точки пересечения очерков заданных поверхностей
до наиболее удаленной точки пересечения очерков заданных поверхностей  (рис. 77).
(рис. 77).
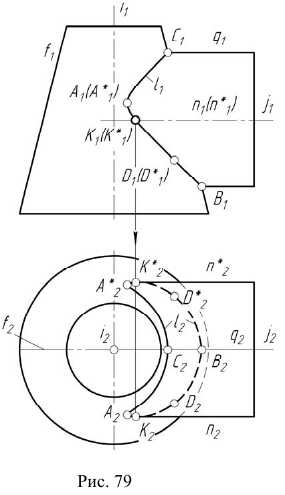
3. Строим фронтальный очерк сферы произвольного радиуса из диапазона 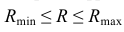 (рис. 78).
(рис. 78).
Сфера радиуса R пересекает коническую и цилиндрическую поверхности по окружностям с и d соответственно. На пересечении этих окружностей определится еще одна пара общих точек заданных поверхностей: 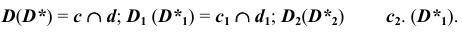
Для построения других точек искомой линии 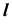 повторим последовательность построений п. 3 данной задачи.
повторим последовательность построений п. 3 данной задачи.
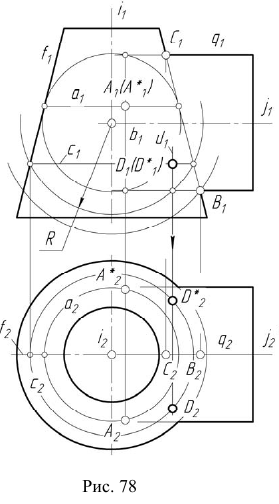
4. Определим проекции точек изменения видимости линии 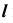 при проецировании на плоскость
при проецировании на плоскость 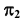 (рис. 79).
(рис. 79).
Отметим фронтальные проекции точек изменения видимости линии 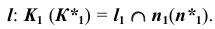 Горизонтальные проекции
Горизонтальные проекции 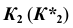 будут принадлежать соответствующим горизонтальным очерковым прямым
будут принадлежать соответствующим горизонтальным очерковым прямым 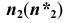 цилиндрической поверхности.
цилиндрической поверхности.
5. Определим видимость линии 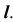
При проецировании на плоскость 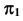 видимая и невидимая части линии
видимая и невидимая части линии 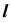 совпадают, так как общая плоскость симметрии поверхностей параллельна фронтальной плоскости проекций.
совпадают, так как общая плоскость симметрии поверхностей параллельна фронтальной плоскости проекций.
Видимость при проецировании на горизонтальную плоскость проекций ограничивает цилиндр. Поэтому видимость линии на 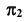 определится, например, положением точки C. Точка C принадлежит видимой части сферы, следовательно, часть линии
определится, например, положением точки C. Точка C принадлежит видимой части сферы, следовательно, часть линии 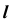 от точки K до точки
от точки K до точки 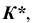 содержащая точку C, — видимая. В поле проекций
содержащая точку C, — видимая. В поле проекций 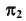 этот участок
этот участок 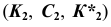 отмечен сплошной основной линией (рис. 79), а участок
отмечен сплошной основной линией (рис. 79), а участок 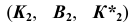 — штриховой.
— штриховой.
Частные случаи пересечения поверхностей вращения второго порядка
К поверхностям второго порядка относятся линейчатые поверхности вращения, а также поверхности, образованные вращением кривой второго порядка вокруг оси симметрии этой кривой.
Теорема Монжа
Если две поверхности второго порядка вписаны в третью поверхность второго порядка или описаны вокруг нее, то линия их пересечения распадается на две кривые второго порядка.
На рис. 80, а изображены цилиндрическая и коническая поверхности вращения, описанные вокруг сферы.
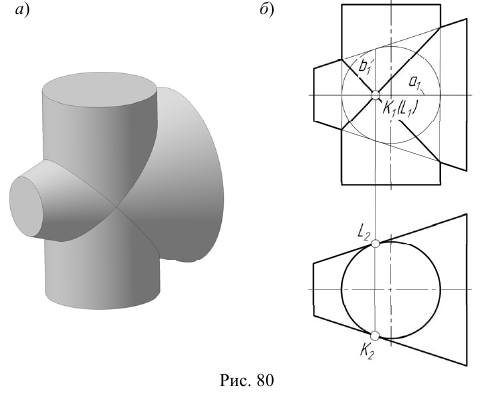
Цилиндрическая и коническая поверхности касаются сферы по окружностям 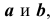 которые пересекаются в точках K и L. Через эти точки и будут проходить линии пересечения рассматриваемых поверхностей (рис. 80, б).
которые пересекаются в точках K и L. Через эти точки и будут проходить линии пересечения рассматриваемых поверхностей (рис. 80, б).
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Способы преобразования чертежа
- Ортогональное проецирование: точка, прямая, плоскость
- Взаимное расположение геометрических образов и фигур
- Преобразование чертежа
- Моделирование плоскости на эпюре Монжа
- Моделирование поверхностей на эпюре Монжа
- Пересечение прямой с плоскостью
- Пересечение прямой с поверхностью