Пересечение многогранников плоскостями в начертательной геометрии с примером

Пересечение многогранников плоскостями:

Гранной поверхностью называется поверхность, образованная пе­ремещением прямолинейной образующей по ломаной направляющей.

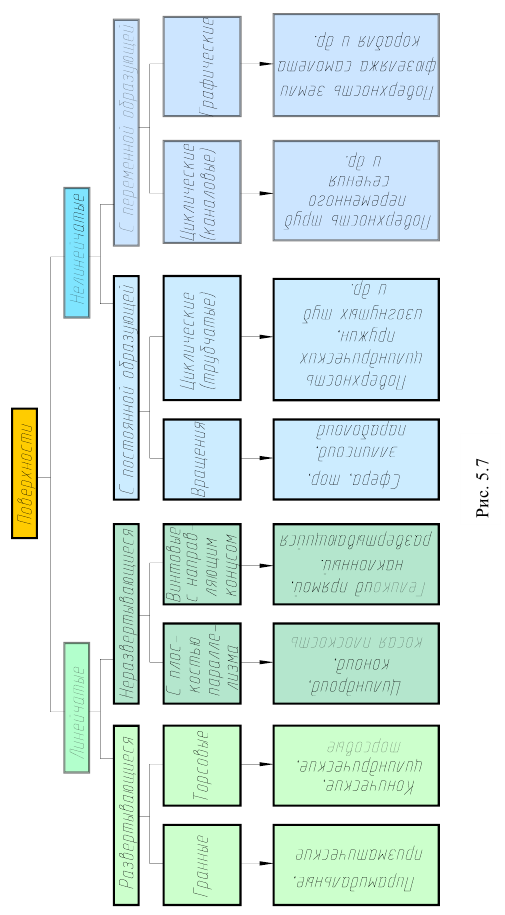
Гранные поверхности можно разделить на два вида: пирамидальные (рис. 5.6, а) и призматические (рис. 5.6, б).

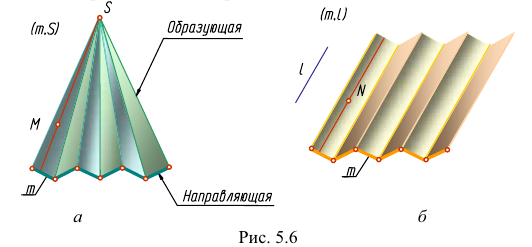
Пирамидальной называется поверхность, образованная перемещением прямолинейной образующей по ломаной направляющей. При этом все образующие проходят через некоторую неподвижную точку S. Определитель поверхности - ломаная направляющая 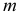и точка S.

Призматической называется поверхность, образованная перемещением прямолинейной образующей по ломаной направляющей. При этом все образующие проходят параллельно некоторому заданному на­правлению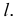

Определитель поверхности - ломаная направляющая 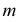и направление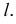

Если образующие призматической поверхности перпендикулярны плоскости проекций, то такую поверхность называют проецирующей. Точки М и N принадлежат соответственно пирамидальной и призматической поверхностям, так как принадлежат прямым, расположенным на этих поверхностях.

Часть пространства, ограниченная со всех сторон поверхностью, называется телом.

Многогранником называется тело, ограниченное плоскими много­угольниками. Рассмотрим два многогранника - призму и пирамиду.

Призмой называется многогранник, у которого основания - равные многоугольники с соответственно параллельными сторонами. Бо­ковые грани призмы - параллелограммы. Если ребра боковых граней перпендикулярны основанию, то призму называют прямой.

Для задания призмы достаточно задать одно ее основание и боковое ребро (рис. 5.8, а).

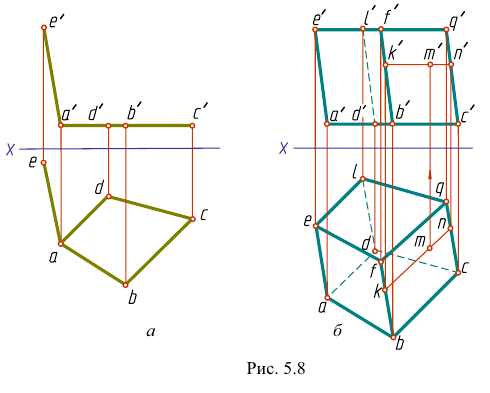
Затем строим ребра 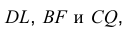параллельные и равные заданному ребру АЕ. Точки 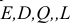L определят второе основание, а тем самым и все грани призмы (рис. 5.8, б). Чертеж в этом случае приобретает большую наглядность. Чтобы построить недостающую проекцию точки, лежащей на грани многогранника, нужно через эту точку провести прямую. Например, если задана горизонтальная проекция точки М, принадлежащей грани 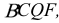то для построения ее фронтальной проекции нужно через эту точку провести прямую KN. Тогда 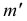определится как точка, принадле­жащая проекции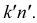

Пересечение многогранников плоскостями

В пересечении гранных поверхностей плоскостями получаются многоугольники. Их вершины определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью.

Многоугольник сечения может быть построен двумя способами:

1. Вершины многоугольника находятся как точки пересечения прямых (ребер) с секущей плоскостью;
2. Стороны многоугольника находятся как линии пересечения плоскостей (граней) многогранника с секущей плоскостью.

В качестве примера построим сечение пирамиды фронтально- проецирующей плоскостью Р (рис. 5.13).

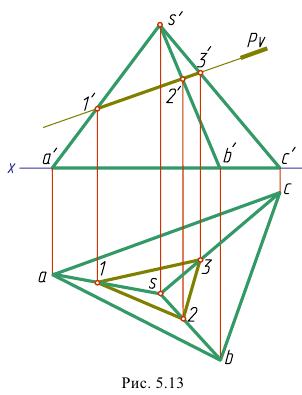
Секущая плоскость является фронтально-проецирующей, следовательно, все линии, лежащие в этой плоскости (в том числе и фигура сечения на фронтальной проекции), совпадут с фронтальным следом 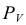плоскости Р. Таким образом, фронтальная проекция фи­гуры сечения 1'2'3' определится при пересечении фронтальных проекций ребер пирамиды со сле­дом 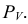Горизонтальные проекции точек 1,2 и 3 находим при помощи линий связи на горизонтальных проекциях соответствующих ребер.