Переходные процессы в нелинейных цепях

Содержание:

Переходные процессы в нелинейных цепях:

Переходные процессы в линейных цепях постоянного и периодического тока заканчиваются установившимся режимом также постоянного или периодического тока. В нелинейных же цепях возможен периодический ток при постоянном напряжении, а также явление неустойчивости режима в цепях постоянного тока.

Пусть в установившемся режиме нелинейная цепь постоянного тока находится в равновесии—токи и напряжения ветвей цепи постоянны. На практике в цепи возможны кратковременные внешние воздействия, выводящие ее из состояния равновесия. Если после прекращения этих воздействий цепь возвращается в исходное состояние, равновесие является устойчивым, если не возвращается — равновесие считается неустойчивым. В отличие от линейной цепи, в которой при заданных условиях возможен только один устойчивый режим, нелинейная цепь может иметь несколько состояний равновесия — устойчивых и неустойчивых.

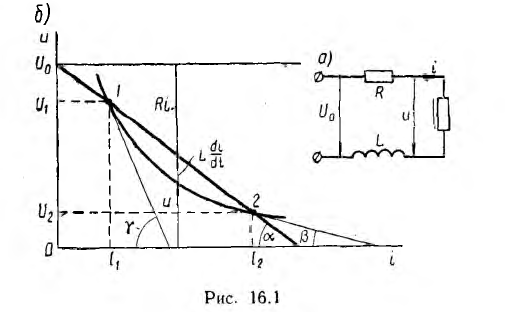
Далее задача устойчивости рассматривается на простом примере цепи рис. 16.1, а с последовательным соединением участков с линейным сопротивлением R, линейной индуктивностью L и нелинейным сопротивлением с падающей вольтамперной характеристикой (рис. 16.1, б). Такую характеристику имеет, например, электрическая дуга. К цепи приложено постоянное напряжение U₀ на рис. 16.1, б нанесена также прямая U₀ — Ri, пересекающая характеристику дуги в точках 1 и 2. Этим двум точкам соответствуют, очевидно, равновесные режимы постоянного тока I, когда по второму закону Кирхгофа

где U — напряжение на дуге; для точки 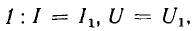, для точки 2: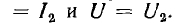

Пусть ток цепи получил кратковременное приращение 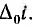. Ему ответствует приращение напряжения на дуге 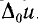. Тогда начнется переходный процесс, во время которого приращения 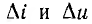и изменяются. Ток цепи и напряжение на дуге будут 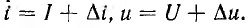На катушке возникает напряжение 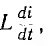уравновешивающее ее э. д. с. самоиндукции. Тогда

Откуда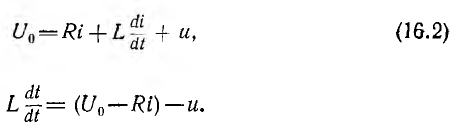

Если U₀ — Ri > u, что имеет место на участке 1—2 характеристики, 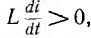, т. е. ток будет возрастать до значения I₂ равновесного режима в точке 2. Если ток получит кратковременное значение, меньшее, чем I₁ или большее, чем 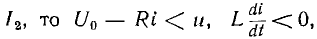т.е.

ток будет уменьшаться в первом случае до нуля, во втором — до равновесного значения I₂. Таким образом, в точке 1 равновесие неустойчиво, в точке 2 — устойчиво.

Математический анализ устойчивости упрощается, когда возможны лишь малые отклонения 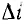тока от положения равновесия. Это позволяет применить метод малых приращений, считая дифференциальное сопротивление 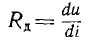: нелинейного элемента вблизи равновесных точек постоянным. Тогда

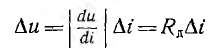
и так как 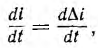уравнение (16.2) получает вид:

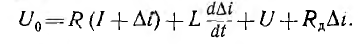
Вычитание из него уравнения равновесия (16.1) дает линейное уравнение для приращения тока вместо исходного нелинейного уравнения (16.2):

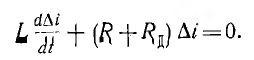
Характеристическое уравнение и его корень:

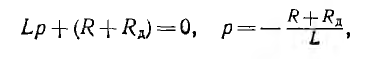
и решение для 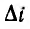с учетом его начального значения 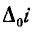будет:

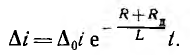
Для падающей вольтамперной характеристики нелинейного элeмента R_Д < 0. Если R + R_д > 0, т. е. угол а, образуемый прямой U₀ — Ri с осью абсцисс, больше угла β, образуемого касательной к характеристике в точке 2 (см. рис. 16.1, б), 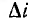приближается к нулю с ростом времени t. Следовательно, точка 2 является точкой устойчивого равновесия.

Если R + R_д < 0, т. е. угол а меньше угла у, образуемого касательной к характеристике в точке 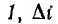с ростом t увеличивается, т. е. точка 1 является точкой неустойчивого равновесия. Даже весьма малое отклонение от нее приведет при 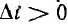к переходу в точку 2, а при 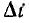< 0 к i = 0, т. е. к погасанию дуги.

Для анализа устойчивости в общем случае сложной цепи постоянного тока, содержащей участки с нелинейными сопротивлениями и с линейными R, L и С, можно также пользоваться методом малых приращений.

Методы расчета переходных процессов

В цепях с сосредоточенными параметрами энергия электрического поля в емкостях по существу определяется их зарядами q, энергия магнитного поля в индуктивностях — их потокосцеплениями ψ. В линейных цепях эти величины пропорциональны соответственно напряжению 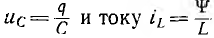откуда из невозможности скачков энергии, т. е. ее мгновенного изменения на конечную величину, вытекает невозможность скачкообразного изменения как 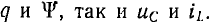. Последнее и использовалось в гл. XV для определения начальных условий при расчете переходных процессов.

В нелинейных цепях зависимости 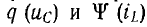нелинейны и возможны, например при гистерезисе, нулевые значения u_с и i_L при ненулевых значениях q и ψ, и наоборот. Поэтому для определения начальных условий на основе невозможности скачкообразного изменения энергии правильней исходить из невозможности скачков q и ψ. Затем, определив зависимости q (t) и ψ (t) и используя кривые q(u_с) и ψ(i_L), можно найти зависимости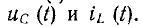

Переходные процессы в нелинейных цепях описываются нелинейными дифференциальными уравнениями. Эти уравнения не имеют общего метода решения.

Для решения этих уравнений применяются приближенные аналитические, графоаналитические и графические методы. Далее на примерах, имеющих практическое значение, показывается применение следующих основных методов, частично использованных ранее при анализе установившихся режимов в нелинейных цепях:

1. Деление процесса на последовательные интервалы времени внутри которых нелинейное уравнение заменяется линейными уравнениями с постоянными коэффициентами.
2. Линеаризация второстепенных членов уравнения, превращающая уравнение в линейное, с возможностью применения последовательных приближений.
3. Кусочно-линейная аппроксимация нелинейной характеристики ломаной прямой, для прямолинейных участков которой составляются решаются линейные уравнения с последующим припасовыванием предыдущих и последующих участков.
4. Аналитическая аппроксимация нелинейной характеристики, юзволяющая получить аналитическое решение дифференциального уравнения переходного процесса.
5. Графическое интегрирование кривой, построенной таким образом, чтобы ограниченная ею площадь была пропорциональной времени, соответствующему каждому значению исследуемой функции; этот метод применим для уравнений первого порядка, допускающих разделение переменных.

Метод линеаризации интервалов на примере автоколебательной цепи

Автоколебательной цепью называется цепь, в которой возникают периодические незатухающие колебания (переменный ток), хотя она питается от источника постоянного напряжения. Подобное явление возможно только в нелинейной цепи. Например, периодический переменный ток может возникнуть в электрической цепи рис. 16.2.

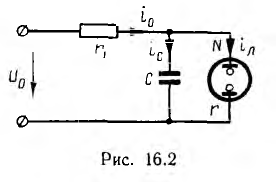
Здесь U₀ — постоянное напряжение источника, r₁ —постоянное сопротивление, С — конденсатор, N — газоразрядная неоновая лампа, которая зажигается при напряжении U₃ и гаснет при меньшем его значении U_r.

В этой цепи периодически происходит зарядка конденсатора до напряжения U₃ и затем разряд на лампу до напряжения U_r. Таким образом, сопротивление ветви с лампой меняется от некоторого значения r, когда она горит, до бесконечности при ее погасании; поэтому цепь является нелинейной. Однако задача может быть линеаризована, если разделить весь период на два интервала, для каждого из которых цепь может считаться линейной, — интервал зарядки и интервал разряда конденсатора. Напряжение конденсатора при его зарядке от источника U₀ 

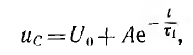
где 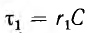— постоянная времени, а А — постоянная интегрирования. В начальный момент u_с (0) = U_r, тогда

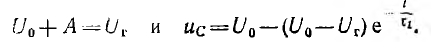
В конце зарядки

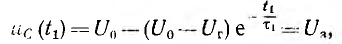
следовательно, время зарядки конденсатора

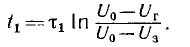
В момент t= t₁ лампа зажигается и начинается разряд конденсатора на лампу. Если для этого интервала пренебречь, ввиду относительно большой величины с током i₀ о источника U₀ и в первом приближении считать сопротивление r горящей лампы постоянным напряжение на конденсаторе 

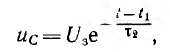
где 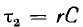— новая постоянная времени. Так как напряжение конденсатора становится равным U_r при 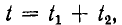а 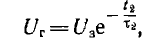время разряда конденсатора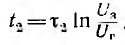

Период колебательного процесса

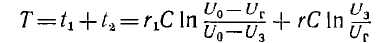
можно регулировать, изменяя г₁ и C₁

На рис. 16.3 изображены кривые изменения напряжения на конденсаторе и на лампе (u_с = u_л), токов i_С конденсатора и i_л лампы.

Методы расчета переходных процессов на примере включения катушки индуктивности со стальным сердечником на постоянное напряжение

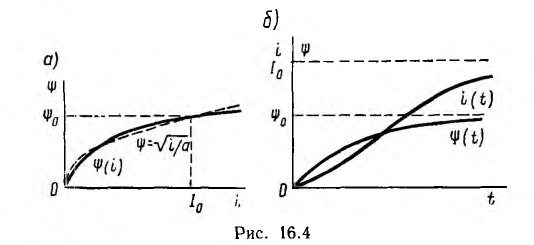
1. Эта задача далее решена методом частичной линеаризации основной кривой ψ (i), т. е. без учета гистерезиса, а также вихревых токов (рис. 16.4, а). При включении катушки на постоянное напряжение U₀ уравнение по второму закону Кирхгофа имеет вид:

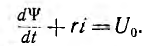
Если в зависимости 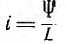считать, применительно ко второму члену уравнения, статическую индуктивность L постоянной, уравнение пре вращается в линейное:

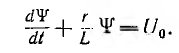
Более точные результаты даст то значение L, которое приобретает индуктивность к концу процесса, когда второй член уравнения велик, например значение 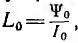, соответствующее принужденным току 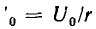и потокосцеплению 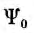(рис. 16.4, а) вытекающая отсюда погрешность во втором члене для начальной части процесса не существенна, так как тогда 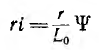мало по сравнению с первым членом уравнения.

Тогда аналогично задаче включения линейной цепи г, L  переходное потокосцепление будет:

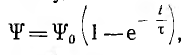
где постоянная времени 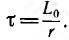. Зависимость 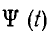показана на рис. 16.4, б; там же изображена соответствующая ей зависимость i (t), построенная для отдельных значений ψ по кривой 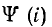рис. 16.4, а.

2. Здесь возможно последующее уточнение решения методом графического интегрирования. Из исходного уравнения следует, что потокосцепление в каждый момент времени t равно

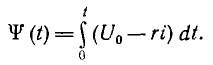
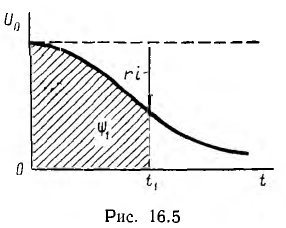
Поэтому, отложив вниз от ординаты U₀ кривую ri (t) (рис. 16.5), построенную на основе полученной зависимости i (t) (см. рис. 16.4, б), можно видеть, что ограниченная этой кривой и осью абсцисс заштрихованная площадь в принятом масштабе пропорциональна ψ₁ для выбранного момента времени t₁. Это позволит построить уточненную кривую ψ(t) и, если она заметно отличается от исходной экспоненты тис. 16.4, б, положить ее в основу повторного построения искомой зависимости i(t).

3. Эта задача может быть решена также методом последовательных равных интервалов времени. Сначала выбирается достаточно малый интервал 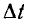(чем он меньше, тем точность больше), например равный 5—10% постоянной временной 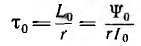цепи с параметрами, соответствующими установившемуся процессу.

Процесс характеризуется величинами потокосцепления ψ и тока в начале и в конце каждого интервала. Величины для конца k-гo интервала удобно давать с индексом k, тогда k — I будет индексом величи для начала этого интервала, равных их значениям для конца предыдущего интервала.

Тогда дифференциальное уравнение цепи

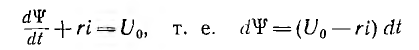
для k-ro интервала получит следующее приближенное решение для приращения потокосцепления за время каждого интервала:

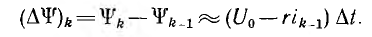
При использовании основной кривой намагничивания в начале первого интервала (t = 0) ψ=0 и i=0; тогда для него

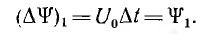
Соответствующий потокосцеплению ψ₁ ток t₁ определяется из кривой намагничивания ψ (i). Приращение потокосцепления во втором интервале

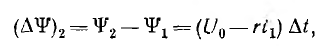
тогда потокосцепление в конце второго интервала 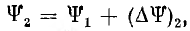для которого по кривой намагничивания определяется ток i₂ и так далее до практического достижения током значения 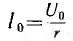установившегося режима. Расчет удобно вести в табличной форме:

По отдельным точкам — значениям i_k из этой таблицы — может быть построена кривая i (t) переходного процесса.

4. Эту же задачу можно решить методом кусочно-линейной аппроксимации, заменив кривую ψ (i), соответствующую основной кривой намагничивания, ломаной, состоящей из прямых участков (рис. 16.6, а). Вместо нелинейного уравнения

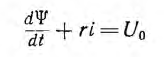
решается линейное, дающее экспоненциальный закон нарастания потокосцепления для каждого прямого участка зависимости ψ (i) но с разными постоянными времени. В отличие от метода интервалов котором конец предыдущего интервала сразу определяет начало следующего, здесь приходится начало каждого участка припасовать концом предыдущего, откуда определяются постоянные интегрирования.

Пусть кривая ψ (i) аппроксимируется ломаной, состоящей из трех участков 0—1, 1—2 и 2—3. Ток и потокосцепление в начале первого участка равны нулю, в его конце и начале второго участка I₁ и ψ₁( конце второго I₂ и ψ₂ и т. д. Дифференциальные индуктивности 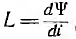для каждого отрезка ломаной, пропорциональны тангенсу его угла а с осью абсцисс. Следовательно, L₁ > L₂ > L₃ (рис. 16.6, б). При переходе к следующему участку дифференциальная индуктивность изменяется скачком.

Сначала для постоянного тока конца переходного процесса 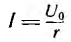по ломаной ψ (i) графически определяется соответствующее ему конечное значение потокосцепления ψ_k.

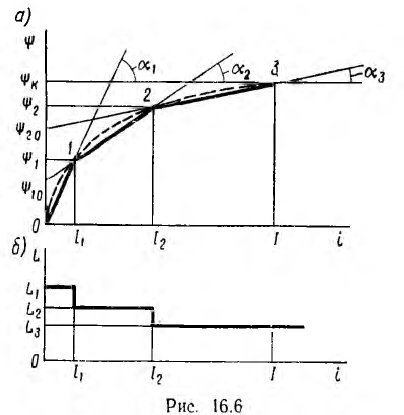
Выражения для потокосцепления на участках 0—1, 1—2 и 2—3 линейной аппроксимации очевидны из рис. 16.6, а; соответственно

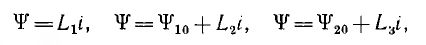
где ψ₁₀ и ψ₂₀ определяются пересечением продолжений отрезков 1—2 и 2—3 ломаной с осью ординат.

По второму закону Кирхгофа уравнение для промежутка времени 0 < t < t₁, где t₁ — время роста потокосцепления ψ с момента включения цепи до значения ψ₁:

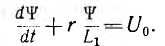
Уравнения для промежутков времени от t₁ до t₂, где t₂ соответствует росту ψ до значения ψ₂ и от t₂ до t = 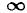, т. е. до конца переходного процесса, такие же, но в них вместо L₁ стоят L₂ и L₃. Так как принужденное значение потокосцепления для этой цепи равно ψ_к, решения этих уравнений для отдельных участков и соответствующих промежутков времени будут:

для 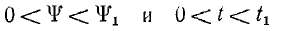постоянные

котором конец предыдущего интервала сразу определяет начало следующего, здесь приходится начало каждого участка припасовать концом предыдущего, откуда определяются постоянные интегрирования.

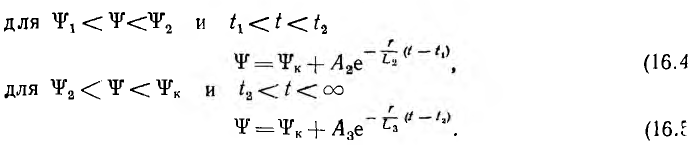
Припасовка в точках 0, 1 к 2 из-за невозможности скачков 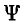позволяв определить постоянные интегрирования А₁, А₂ и А₃ путем приравнивания потокосцепления 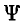из уравнения (16.3) нулю для t = 0, и уравнения (16.4) — потокосцеплению 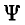₁, для t =t₁ и из уравнения (16.5) — потокосцеплению 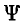₂ для t =t₂

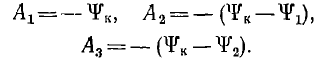
Тогда уравнения (16.3) и (16.4) после подстановки в них, соответственно, t = t₁ и t = t₂ получают вид:

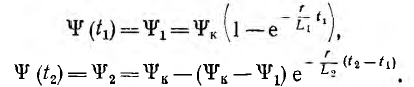
Отсюда определяются моменты времени t₁ и t₂, когда потокосцепление получает значения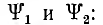

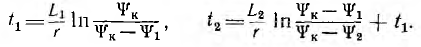
По этим данным на рис.. 16.7 построена зависимость ψ (t) для всех трех участков кусочно-линейной характеристики. Эта кривая имеет изломы при t₁ и t₂ из-за изломов кусочно-линейной аппроксимации ψ(i) в эти моменты времени. В действительности этих изломов ввиду плавности исходной кривой ψ (i) не будет. Поэтому кривую ψ(t) с изломами следует заменить усредненной плавной кривой, проходящей через точки излома, так как соответствующие им точки излома кусочно-линейной аппроксимации расположены на исходной кривой.

Затем по кривой намагничивания ψ(i) можно определить значения тока i, соответствующие отдельным значениям кривой ψ(t) и по ним построить плавную кривую нарастания тока i (t).

5. Эта же задача может быть решена методом аналитической аппроксимации зависимости ψ (i). Наиболее простой аппроксимацией является

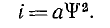
Начальная точка этой зависимости, так же как и кривой ψ (i), совпадает с началом координат, вторую точку совпадения аналитической и графической зависимости удобно выбрать в точке ψ_0, I₀ (см. рис. 16.4, а). Тогда

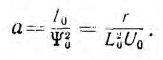
График кривой 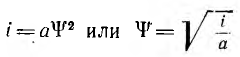показан на рис 16.4, пунктиром.

После подстановки i уравнение цепи получает вид:

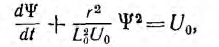
решение относительно t будет:

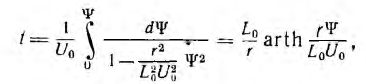
откуда находят искомые зависимости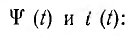

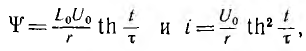
где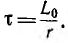

Включение катушки индуктивности со стальным сердечником на синусоидальное напряжение

Уравнение цепи при включении катушки со стальным сердечником на синусоидальное напряжение имеет вид:

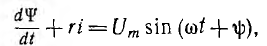
где ψ — фаза включения. Если здесь применить метод линеаризации второстепенного второго члена уравнения, приняв 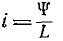- аналогично и зная на примере линейной цепи , что здесь возможны сверхтоки, целесообразно в качестве постоянной статической индуктивности взять ее значение из кривой 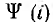по крайней мере для амплитудных значений потокосцепления и тока установившегося режима, т. е. принять 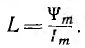Тогда получается линейное уравнение

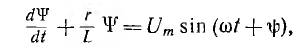
аналогичное решенному , и, следовательно, переходное потокосцепление

где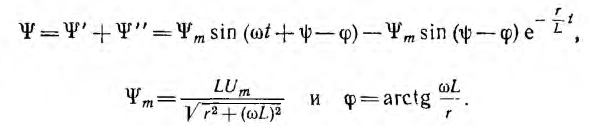

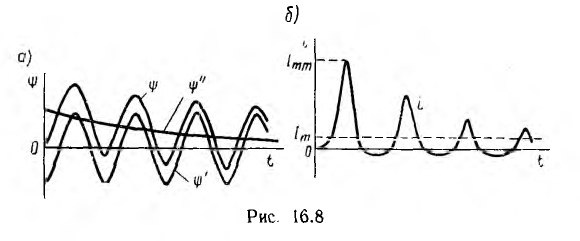
При включении в момент, когда 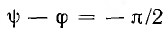(рис. 16.8, а), три большой постоянной времени наибольшее значение потокосцепления будет немногим меньше 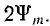По отдельным точкам кривой ψ (t) и по характеристике ψ (I) (см. рис. 16.4, а) строится кривая i(t) (рис. 16.8, б). Если точка ψ_m,I_m принужденного режима кривой ψ (i) лежит за коленом кривой, сверхток I_mm может быть весь значительным, превышая I_m в десятки раз. Это очень существенно при включении трансформатора с разомкнутой вторичной обмоткой, так как при этом он эквивалентен катушке. Включение в указанный и близкий момент может дать сверхток, превышающий ток при аварийном коротком замыкании вторичной цепи.

Если в рассматриваемой цепи ее сопротивление г относительно велико, второй член ri уравнения может оказаться первостепенным и правильней линеаризовать не его, а второй член 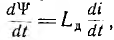считая динамическую индуктивность L_д= const. Тогда задача будет аналогична решенной  и ток i (t) представится суммой экспоненты и синусоиды. Пользуясь графиком ψ(i) по точкам кривой i (t) можно построить кривую ψ (t), полуволны которой будут иметь более тупую форму.

Изображение переходных процессов в фазовой плоскости

До сих пор переходные процессы в линейных и нелинейных цепях рассматривались в функции времени. Весьма наглядным является также изображение процессов в фазовой плоскости, по ocи абсцисс которой откладывается исследуемая величина х, по оси ординат — скорость ее изменения 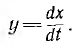Они определяют изображающую точку х, у, соответствующую данному состояния цепи. При изменении состояния цепи точка перемещается по фазовой траектории х (у).

Пусть, например, рассматривается процесс короткого замыкания линейной цепи г, L (см. рис:. 15.1, а), описываемый дифференциальньным уравнением

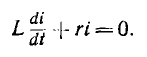
Если обозначить 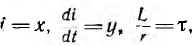уравнение принимает вид

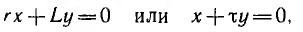
его фазовая траектория изобразится прямой, проходящей через начало координат во втором или четвертом квадранте и составляющей осью абсцисс угол 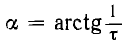(рис. 16.9). Стрелки показывают направление движения изображающей точки при переходном процессе.

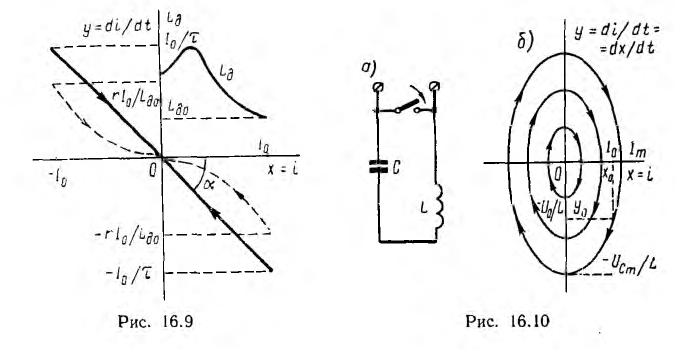
Координаты начальной точки 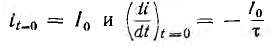или, соответственно, —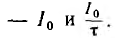

Тот же процесс в нелинейной цепи с индуктивностью, зависящей от тока, описывается таким же уравнением, но в него вместо постоянной индуктивности L нужно подставить динамическую индуктивность Если при токе I₀ ее начальное значение 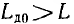и с уменьшением тока изменяется по кривой, показанной в первом квадранте на рис. 16.9, а сопротивление г цепи остается тем же, фазовая траектория будет иметь вид, показанный на том же рисунке прерывистой линией.

Процесс короткого замыкания линейной цепи с последовательным соединением индуктивности L и емкости С (рис. 16.10, а) описывается уравнением

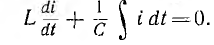
В результате дифференцирования этого уравнения и его деления на L

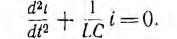
после введения обозначений

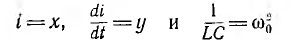
вторая производная

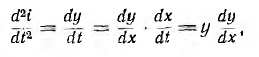
и уравнение принимает вид:

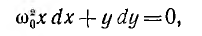
а после интегрирования

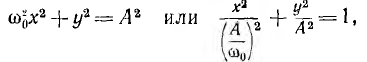
где А — постоянная интегрирования, определяемая начальными условиями. Если начальные значения тока цепи i (0) = I₀ = х₀ и напряжения на емкости u_с (0)= U_c0. и так как в начальный момент

то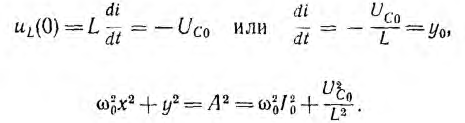

Как видно из уравнения, фазовая траектория представляет собой эллипс (рис. 16.10, б), тем самым изображая незатухающие колебания. Очевидно, что вертикальная и горизонтальная полуоси эллипса соответственно равны:

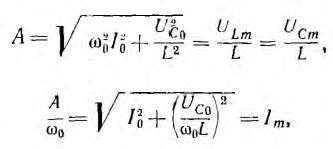
т. е. вертикальная полуось пропорциональна максимальным значениям напряжения на индуктивности и емкости, горизонтальная полуось равна максимальному значению тока, а их отношение — частоте (i>0 незатухающих колебаний.

Изображающая точка х₀, у₀ есть точка начала процесса, который дальше идет в направлении, указанном стрелкой. В верхней полуплоскости 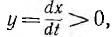т.е. х увеличивается и изображающая точка движется слева направо, а в нижней — справа налево, так как у < 0 и х убывает. При другой начальной точке, не лежащей на данном эллипсе, фазовая траектория будет также эллипсом, но с другими величинами полуосей. Начало координат в этом случае называется центром равновесия.

При разряде конденсатора с напряжением U_со на цепь с, r и l (рис. 16.11, а) и 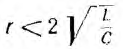с происходит затухающий колебательный процесс и фазовые траектории получают вид спиралей (рис. 16.11, б), по которым изображающая точка движется от точки 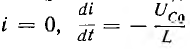к началу координат, называемому в этом случае устойчивым фокусом.

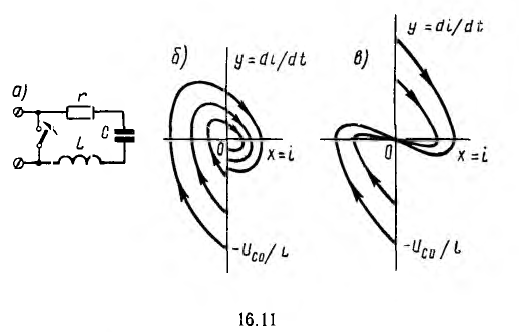
При 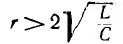спирали превращаются в параболические кривые (рис. 16.11, в), также приходящие в начало координат — устойчивый узел.

Изображение процессов в фазовой плоскости позволяет решать многие задачи линейной и нелинейной электротехники по виду фазовой траектории без решения в общем виде дифференциальных уравнений.