
Переходные процессы в колебательных контурах
Содержание:
Переходные процессы в колебательных контурах:
В современных системах телекоммуникации, построенных на принципах цифровой обработки сигналов, сообщения представляются в виде последовательностей одно- или двухполярных импульсов напряжения или тока. Формы импульсов могут быть различными. Здесь рассматриваются только прямоугольные импульсы.
Одиночный прямоугольный импульс с фиксированными длительностью 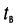
Импульсы в последовательности могут иметь как строго определённую длительность, так и переменную, обычно кратную длительности одного видеоимпульса 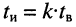
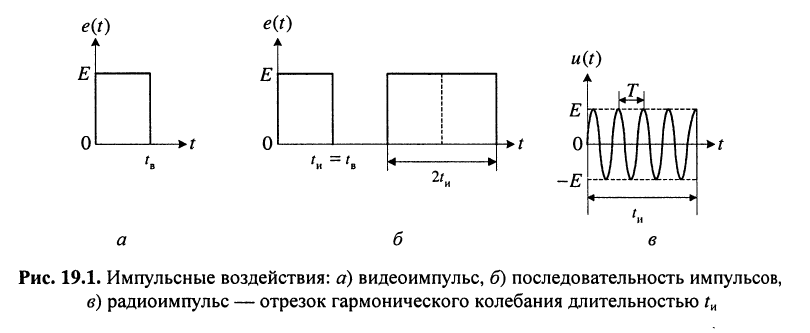
Однако в канал связи собственно импульсы, за редким исключением, не передаются. Они заменяются отрезками гармонического колебания (рис. 19.1, в) длительностью 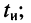 период гармонического колебания Т на отрезке всегда
период гармонического колебания Т на отрезке всегда
существенно меньше наименьшей длительности импульса 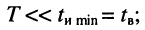 такие импульсы называют радиоимпульсами, а отрезок гармонического колебания часто называют высокочастотным заполнением.
такие импульсы называют радиоимпульсами, а отрезок гармонического колебания часто называют высокочастотным заполнением.
Свободные колебания в RC-цепи при воздействии видеоимпульса
Задача 19.1.
Определить закон изменения напряжения на ёмкости в RС-цепи при воздействии видеоимпульса (рис. 19.2) при нулевых начальных условиях.
Решение. Реакцию на видеоимпульс можно определить, воспользовавшись принципом суперпозиции, а именно: представить видеоимпульс
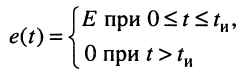
как сумму двух ступенчатых воздействий одинаковых амплитуд 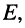 одно из которых задержано на
одно из которых задержано на 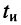 (рис. 19.2, а—в):
(рис. 19.2, а—в):
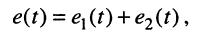
где
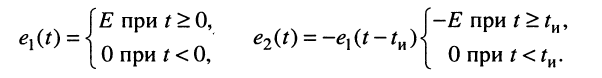
Тогда в силу линейности цепи реакция 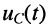 на сумму воздействий будет равна сумме реакций на каждое из воздействий
на сумму воздействий будет равна сумме реакций на каждое из воздействий
(рис. 19.2, г—е):
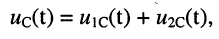
где согласно (18.3) имеем:
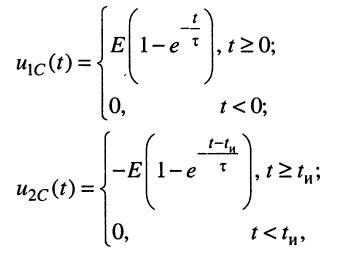
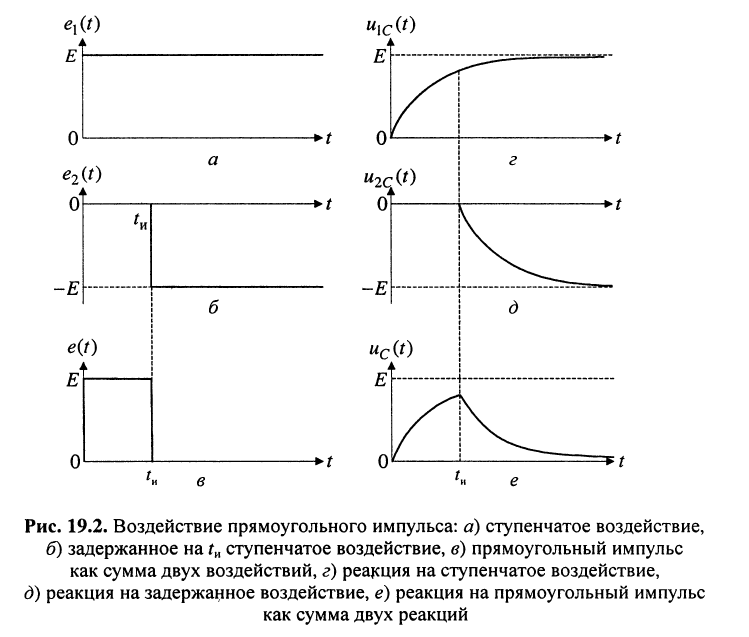
а реакция запишется как сумма полученных колебаний:
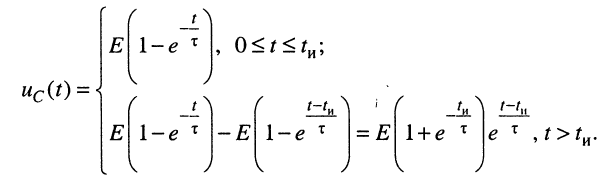 (19.1)
(19.1)
Полученные выражения и рисунок показывают, что за время переходного процесса, ограниченное длительностью видеоимпульса 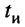 , ёмкость может не успеть зарядиться до значения Е , а по окончании воздействия видеоимпульса происходит процесс разряда ёмкости. При этом чем больше постоянная времени
, ёмкость может не успеть зарядиться до значения Е , а по окончании воздействия видеоимпульса происходит процесс разряда ёмкости. При этом чем больше постоянная времени 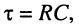 тем длительнее оказываются переходные процессы заряда и разряда ёмкости, т. е. тем медленнее заряжается ёмкость и тем меньшим оказывается напряжение заряда
тем длительнее оказываются переходные процессы заряда и разряда ёмкости, т. е. тем медленнее заряжается ёмкость и тем меньшим оказывается напряжение заряда 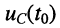 к моменту окончания воздействия видеоимпульса.
к моменту окончания воздействия видеоимпульса.
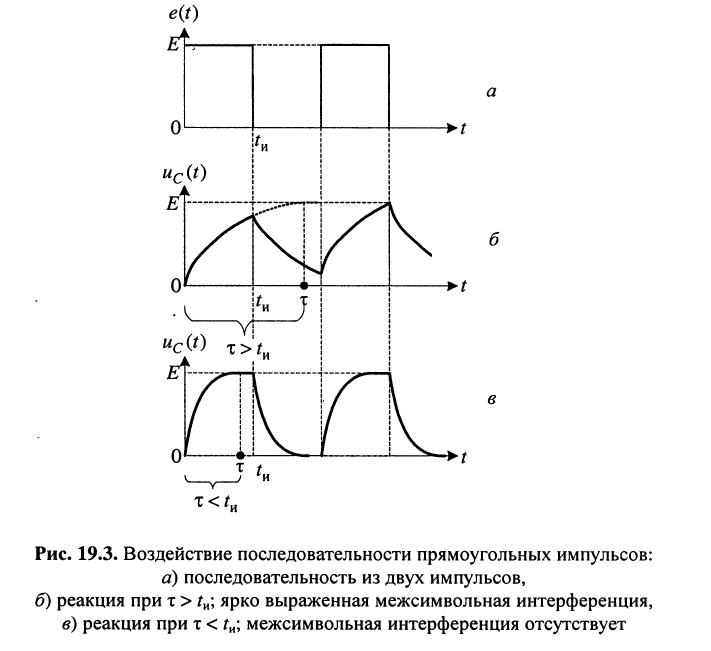
Посмотрим, к чему может привести такое явление при передаче по системе связи не одного, а последовательности импульсов
(рис. 19.3, а), что имеет место в действительности. Если очередной импульс будет передаваться прежде, чем завершится разряд ёмкости1, произойдёт перекрытие, или наложение двух переходных процессов. В результате разряд ёмкости прекратится, и её заряд начнётся не с нуля, а с некоторого напряжения, достигнутого на ёмкости к этому моменту (рис. 19.3, б), т. е. последует частичное перекрытие соседних импульсов во времени, которое приведёт к искажению передаваемых и принимаемых импульсов. Причём от импульса к импульсу искажения будут нарастать.
Искажения такого рода называются межсимвольной интерференцией. Рассмотренное перекрытие соседних импульсов является наиболее простым примером межсимвольной интерференции. Борьба с межсимвольной интерференцией является весьма сложной и актуальной задачей.
Разряд считается завершённым, если напряжение на ёмкости не превышает 0,01 амплитуды Е.
Наиболее остро эта задача стоит перед разработчиками средств современной беспроводной связи, которые весьма широко используются в офисных и домашних сетях передачи информации, в интерфейсах "ноутбук — настольный компьютер", для обеспечения беспроводного доступа в Интернет, для организации сотовой связи. Скорость передачи данных в таких сетях исчисляется в десятках и сотнях гигагерц и имеет тенденцию к дальнейшему её росту.
Для передачи последовательности импульсов с такими скоростями без искажений требуется ряд условий, которые предъявляются к конкретным системам связи и которые изучаются в других дисциплинах.
Добиться исключения межсимвольной интерференции на этапе формирования первичных импульсов и ускорить процесс разряда ёмкости можно, если потребовать, чтобы постоянная времени была не больше длительности видеоимпульса (рис. 19.3, в):
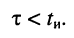 (19.2)
(19.2)
Свободные колебания в параллельном контуре без потерь
Параллельные и последовательные колебательные контуры являются основой избирательных фильтров, амплитудных и фазовых корректоров и входят в состав полосовых усилителей. Свойства перечисленных устройств зависят от свойств колебательных контуров, которые изучим при различных воздействиях.
Задача 19.2.
Пусть до момента t = 0 размыкания ключа цепь находилась в режиме постоянного тока: через индуктивность протекал постоянный ток 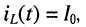 а напряжение на ёмкости равнялось нулю. Следовательно, в момент коммутации начальные условия не являются нулевыми и описываются равенствами:
а напряжение на ёмкости равнялось нулю. Следовательно, в момент коммутации начальные условия не являются нулевыми и описываются равенствами:

Найти законы изменения тока в контуре 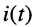 и напряжения на контуре
и напряжения на контуре 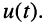
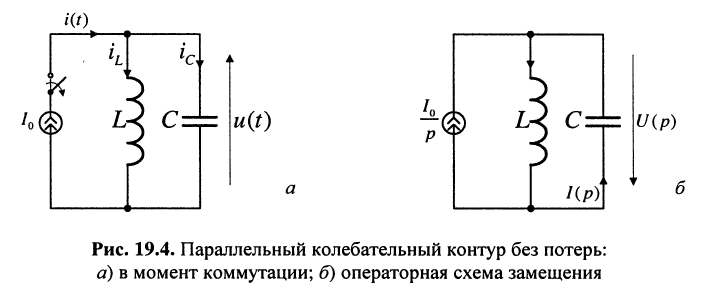
Решение. Для исследования процессов, происходящих в контуре после коммутации, воспользуемся операторным методом и запишем изображение напряжения на контуре:
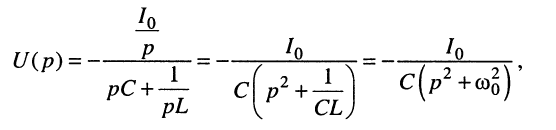 (19.3)
(19.3)
где
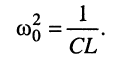
Умножая числитель и знаменатель (19.3) на 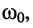 получаем табличную функцию
получаем табличную функцию
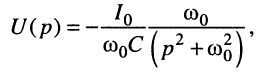
которой соответствует оригинал (см. табл. 16.1, строка № 10):
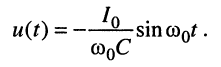 (19.4)
(19.4)
Для определения закона изменения тока в контуре воспользуемся законом Ома в операторной форме
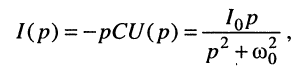
которой соответствует оригинал (см. табл. 16.1 строка № 11):
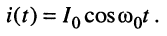 (19.5)
(19.5)
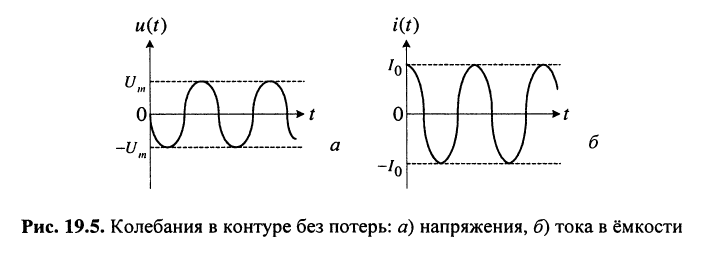
Графики временной зависимости напряжения и тока в контуре без потерь представлены на рис. 19.5.
Заметим, что выражение (19.3) является изображением решения линейного однородного дифференциального уравнения второго порядка, которое описывает процесс свободных колебаний в контуре:
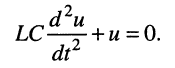
Его характеристическое уравнение
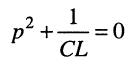
совпадает с характеристическим уравнением выражения (19.3) и имеет пару комплексно сопряжённых мнимых корней
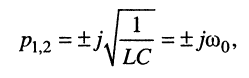
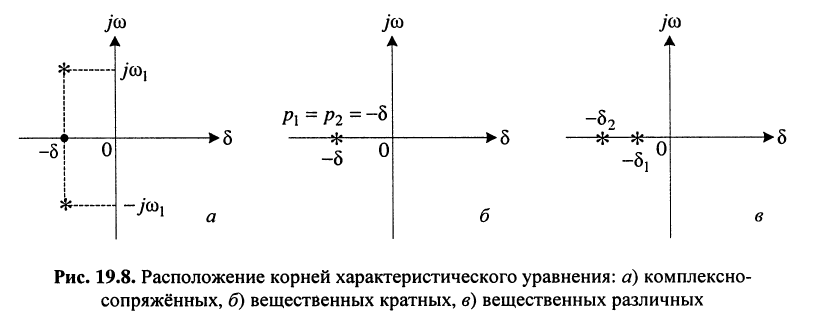
располагающихся на мнимой оси р-плоскости симметрично относительно начала координат (рис. 19.6).
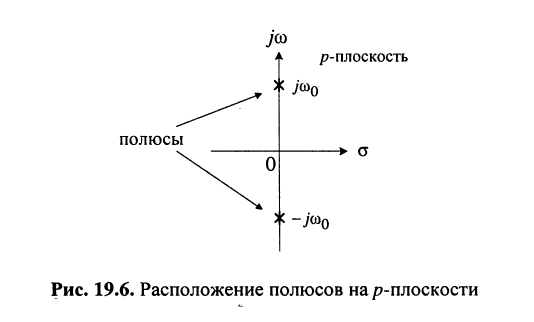
Анализ полученных решений приводит к следующим выводам:
- свободные колебания тока в контуре без потерь и напряжения на его элементах являются отрезками незатухающих гармонических колебаний;
- круговая частота колебаний
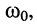 .называемая частотой колебаний контура, определяется только параметрами контура L и С и не зависит от начальных условий;
.называемая частотой колебаний контура, определяется только параметрами контура L и С и не зависит от начальных условий; - начальные условия определяют амплитуды колебаний тока
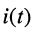 и напряжения
и напряжения 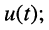
- отношение амплитуд колебаний напряжения и тока в контуре равно его волновому, или характеристическому сопротивлению и не зависит от начальных условий;
- начальные фазы колебаний тока
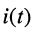 и напряжения
и напряжения 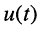 различны и в общем случае зависят от начальных условий.
различны и в общем случае зависят от начальных условий.
Свободные колебания в последовательном RLC-контуре
Незатухающий характер колебаний в рассмотренном идеальном LC-контуре объясняется отсутствием потерь (т. е. активной проводимости G); в этом случае свободные колебания представляют собой периодический процесс перехода энергии из одного вида в другой: из магнитной в электрическую и обратно. Любой реальный контур содержит не идеальные конденсаторы и катушки индуктивности, что приводит к потерям энергии за счёт её рассеяния (см.разд. 3.3). Наличием потерь обусловлен затухающий характер свободных колебаний, что показывается ниже на примере последовательного колебательного RLС-контура, т. е. контура с потерями, что отражается введением резистивного элемента.
Задача 19.3.
Пусть в момент коммутации t(0) к последовательной RL-цепи (рис. 19.7, а) подключена заряженная ёмкость 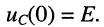 Найти закон изменения тока i(t) в последовательном колебательном RLС-контуре.
Найти закон изменения тока i(t) в последовательном колебательном RLС-контуре.
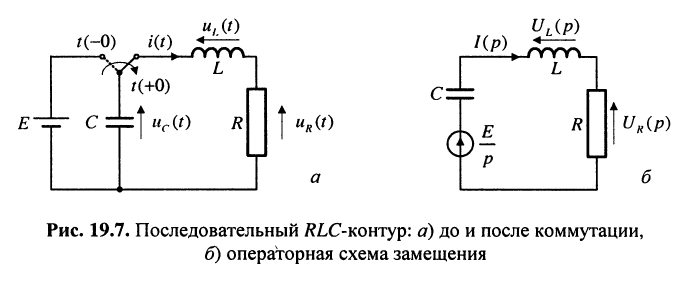
Решение. До коммутации напряжение на ёмкости было равно Е, а ток в индуктивности равнялся нулю. По закону коммутации в образовавшемся RLC-контуре имеем:

Воспользуемся операторной схемой замещения анализируемого контура, для чего, как и в задаче 18.1, представим операторную схему замещения заряженной ёмкости в виде последовательно соединённых источника напряжения 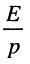 и незаряженной емкости С.
и незаряженной емкости С.
Согласно закону Ома в операторной форме (рис. 19.7, б) изображение реакции (тока) имеет вид:
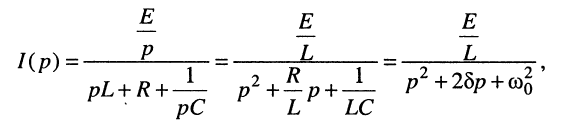 (19.6)
(19.6)
где:
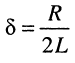 коэффициент затухания контура;
коэффициент затухания контура;
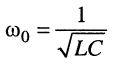 круговая частота собственных колебаний контура без потерь.
круговая частота собственных колебаний контура без потерь.
Для оценки характера свободных колебаний обратимся к характеристическому уравнению рассматриваемой цепи, которое получается приравниванием знаменателя (19.6) нулю:
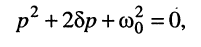 (19.7)
(19.7)
и изучим корни этого уравнения
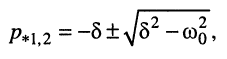 (19.8)
(19.8)
которые являются полюсами функции (19.6).
Поскольку коэффициенты характеристического уравнения вещественны (вследствие вещественности значений параметров R, L и С), его корни (полюсы 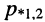 функции (19.6)) согласно основной теореме алгебры могут быть либо вещественными, либо составлять комплексно-сопряжённую пару.
функции (19.6)) согласно основной теореме алгебры могут быть либо вещественными, либо составлять комплексно-сопряжённую пару.
Рассмотрим три возможных случая:
1. Корни (полюсы) комплексно-сопряжённые:
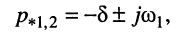
где
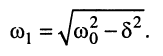 (19.9)
(19.9)
Расположение таких корней на р-плоскости показано на рис. 19.8, а. Такие корни могут быть лишь при условии выполнения неравенства
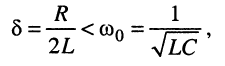
или, что то же самое, при
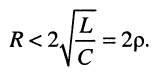
Исходя из таблицы соответствий (см. табл. 16.1, строка № 12)
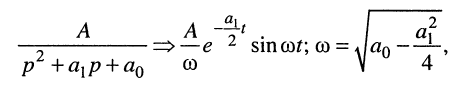
согласно (19.6) получаем формулу для тока в контуре:
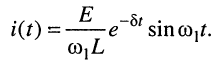 (19.10)
(19.10)
Из последнего выражения видно, что амплитуда колебаний является функцией времени и убывает по экспоненциальному
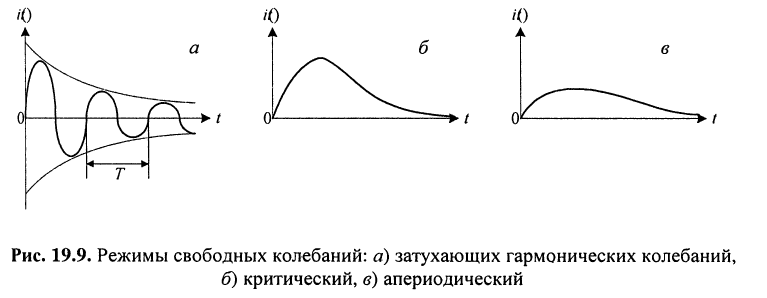
закону 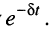 Такой режим свободных колебаний называется режимом затухающих гармонических колебаний (рис. 19.9, а). Скорость убывания амплитуды колебаний зависит от величины коэффициента затухания 5, характеризующего потери в контуре.
Такой режим свободных колебаний называется режимом затухающих гармонических колебаний (рис. 19.9, а). Скорость убывания амплитуды колебаний зависит от величины коэффициента затухания 5, характеризующего потери в контуре.
Частота
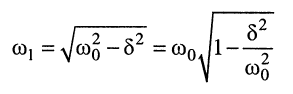 (19.11)
(19.11)
называется частотой собственных затухающих колебаний контура. Она меньше частоты собственных незатухающих колебаний 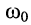 и зависит от значений всех элементов контура, а не только от значений реактивных элементов.
и зависит от значений всех элементов контура, а не только от значений реактивных элементов.
Период затухающих колебаний равен
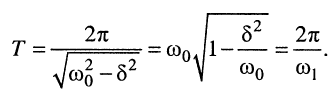 (19.12)
(19.12)
Назовём добротностью контура отношение сопротивления элемента индуктивности к сопротивлению резистивного элемента
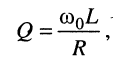
тогда коэффициент затухания примет вид:
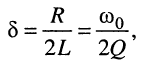
откуда следует, что колебания в контуре убывают тем медленнее, чем выше добротность контура.
Поскольку частота собственных затухающих колебаний контура (19.9), выраженная через добротность, записывается в виде:
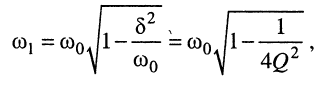
то колебательному режиму в контуре соответствуют значения добротности 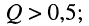 причём чем больше добротность, тем ближе друг к другу частоты
причём чем больше добротность, тем ближе друг к другу частоты 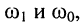 а при
а при 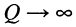 имеет место
имеет место 
Как говорилось ранее (см. задачу 19.1), процесс свободных колебаний считается оконченным, если амплитуда колебаний становится равной 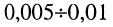 от первоначального значения. Следовательно, длительность свободных колебаний в контуре согласно (19.10) может быть принятой в пределах:
от первоначального значения. Следовательно, длительность свободных колебаний в контуре согласно (19.10) может быть принятой в пределах:
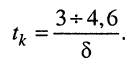
2. Корни характеристического уравнения вещественные кратные.
Если два корня (полюса) равны друг другу 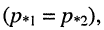 то такие корни называются кратными. В данном случае кратные вещественные корни (полюсы) являются отрицательными и равны
то такие корни называются кратными. В данном случае кратные вещественные корни (полюсы) являются отрицательными и равны
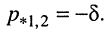
Расположение кратных вещественных корней на р-плоскости показано на рис. 19.8, б. Такие корни согласно (19.8) возможны только при равенстве
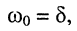
т.е. когда 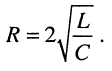
Это — предельный случай колебательного режима, когда частота собственных затухающих колебаний равна нулю:
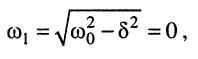
чему соответствует бесконечно большой период колебаний 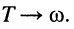 Ток в этом случае имеет вид
Ток в этом случае имеет вид
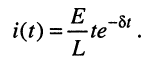
Такой режим свободных колебаний (рис. 19.9, б) называют критическим.
3. Корни вещественные и различные.
Вещественные различные корни можно представить выражением
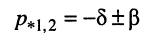
при условии вещественности
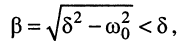
т. е. при 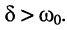 В свою очередь, это означает, что корни являются отрицательными. Расположение корней
В свою очередь, это означает, что корни являются отрицательными. Расположение корней 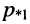 и
и 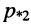 показано на
показано на
рис. 19.8, в. Следовательно, первичные параметры контура должны удовлетворять неравенству:
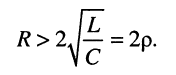
Найдём ток в контуре, для чего преобразуем выражение (19.6)
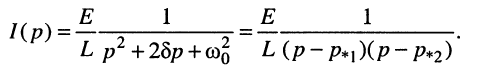
Представим дробь в виде суммы простых дробей
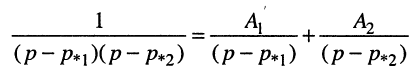
и определим неизвестные коэффициенты разложения 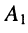 и
и 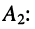
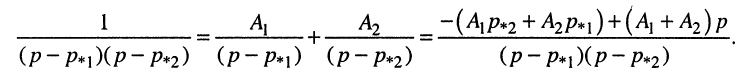
Для равенства левой и правой дробей необходимо, чтобы их числители были равными, поэтому записываем систему уравнений:
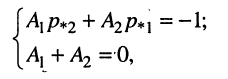
из которой нетрудно получить значения искомых коэффициентов:
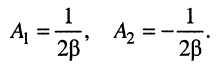
Подставим найденные коэффициенты разложения в формулу операторного тока:
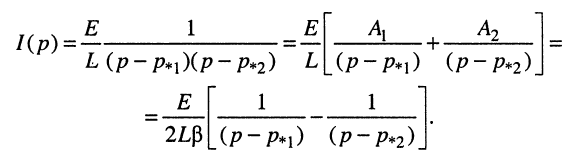
Для получения формулы протекающего в контуре тока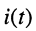 воспользуемся свойством линейности преобразования Лапласа и таблицей соответствий (см. табл. 16.1, строка № 7):
воспользуемся свойством линейности преобразования Лапласа и таблицей соответствий (см. табл. 16.1, строка № 7):
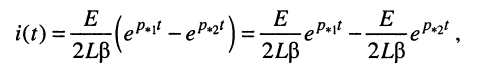
откуда следует, что ток в цепи представляет собой алгебраическую сумму двух экспоненциальных функций, абсолютные значения которых убывают во времени, поскольку корни отрицательны: 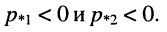
Этот режим (рис. 19.9, в) называется апериодическим.
Колебания в последовательном RLC-контуре при воздействии в виде отрезка гармонического колебания
Задача 19.4.
Пусть при нулевых начальных условиях на последовательный RLC-контур, имеющий резонансную частоту 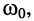 действует отрезок гармонического колебания
действует отрезок гармонического колебания 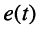 с той же частотой
с той же частотой 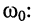
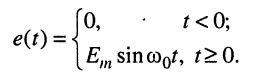
Найти закон изменения тока в контуре.
Решение. Запишем ток в операторной форме согласно закону Ома:
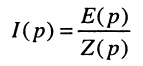
и подставим сюда изображение воздействия
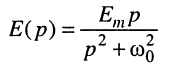
и операторное сопротивление контура
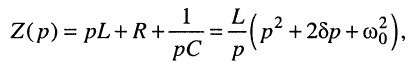
где
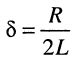 — коэффициент затухания контура,
— коэффициент затухания контура,
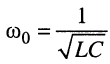 — резонансная частота.
— резонансная частота.
В результате получаем сложную функцию
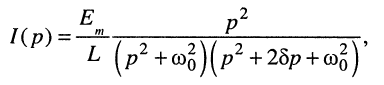 (9.13)
(9.13)
не имеющую табличного соответствия. Для определения оригинала представим (19.13) в виде суммы простых дробей:
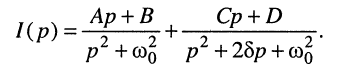 (19.14)
(19.14)
Коэффициенты А, В, С, D определим методом неопределённых коэффициентов, как это было сделано в разд. 19.3.3, для чего приведём дроби (19.14) к общему знаменателю и приравняем числители новой дроби числителю (19.13). После этих несложных преобразований получаем равенство
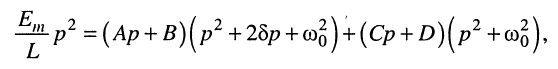
которое, как нетрудно видеть, справедливо при следующих соотношениях между коэффициентами:
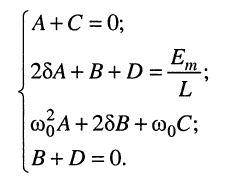
Решение этой системы линейных уравнений даёт:
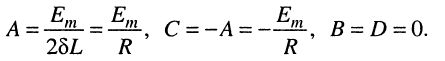
Подставляя коэффициенты в (19.14), имеем:
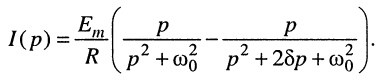
Оригиналы для дробей, стоящих в скобках, известны (см. табл. 16.1), и можно сразу записать выражение для тока:
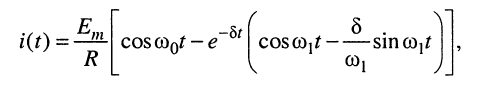 (19.15)
(19.15)
где
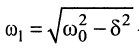 — частота собственных затухающих колебаний контура с потерями.
— частота собственных затухающих колебаний контура с потерями.
Выражение для тока (19.15) существенно упрощается, если учесть, что на практике применяются контуры высокой добротности 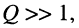 для которых
для которых
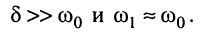
При этих условиях выражение для тока принимает вид:
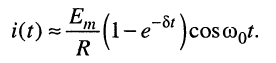 (19.16)
(19.16)
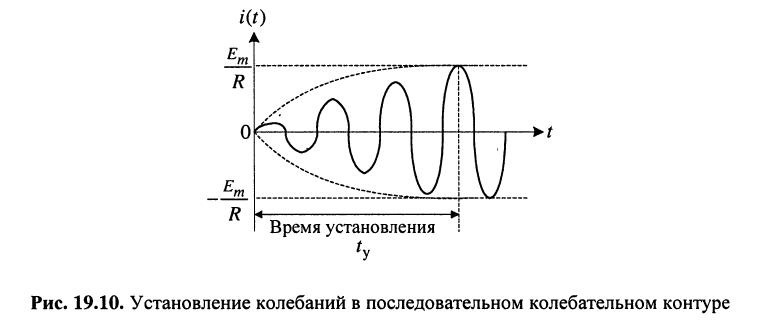
Функция (19.16) описывает колебание (рис. 19.10), которое отличается от гармонического воздействия тем, что его амплитуда возрастает по экспоненциальному закону, стремясь к значению
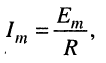
которое принято называть установившимся.
Из (19.16) следует, что нарастание амплитуды тока происходит тем быстрее, чем больше коэффициент затухания контура 5. Напомним, что процесс установления колебаний в контуре происходит за время
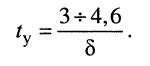
Найдём связь между длительностью переходного процесса 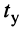 и шириной полосы пропускания контура, для чего подставим в формулу для
и шириной полосы пропускания контура, для чего подставим в формулу для 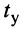 значение
значение 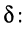
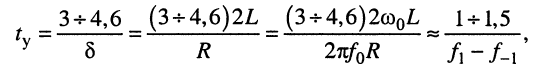
откуда полагают, что
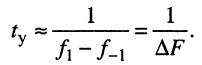 (19.17)
(19.17)
Выводы:
- чем выше добротность контура, т. е. чем уже его полоса пропускания, тем больше длительность переходного процесса, а это, в свою очередь, приводит к большим искажениям формы передаваемого сигнала;
- произведение полосы пропускания контура на длительность переходного процесса в контуре согласно (19.17) приближённо равно единице
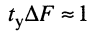 ; это справедливо и для более сложных избирательных цепей.
; это справедливо и для более сложных избирательных цепей.
Прохождение радиоимпульса через колебательный контур
Пусть на контур воздействует радиоимпульс длительности 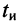 и частотой, равной резонансной частоте контура (рис. 19.11, а):
и частотой, равной резонансной частоте контура (рис. 19.11, а):
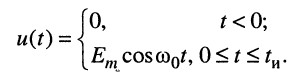
Реакцию контура на радиоимпульс можно найти на основании принципа суперпозиции с учётом полученного в разд. 19.4
решения (19.16).
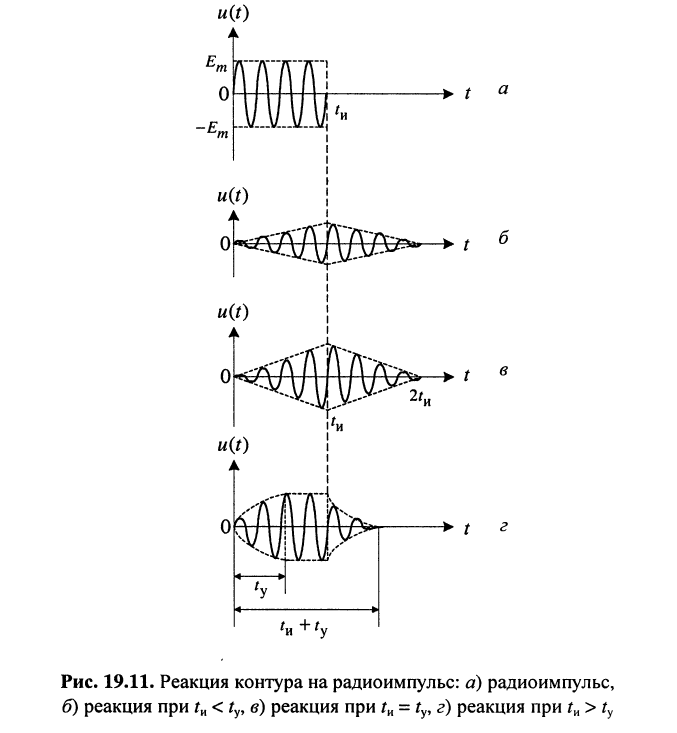
В зависимости от полосы пропускания контура, т. е. от величины коэффициента затухания контура 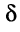 , возможны три типичных случая (рис. 19.11):
, возможны три типичных случая (рис. 19.11):
- Длительность радиоимпульса меньше времени установления колебаний:
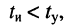 т.е. полоса пропускания контура достаточно узкая (рис. 19.11,6); импульс значительно искажается, поскольку к моменту окончания воздействия колебания в контуре не являются установившимися.
т.е. полоса пропускания контура достаточно узкая (рис. 19.11,6); импульс значительно искажается, поскольку к моменту окончания воздействия колебания в контуре не являются установившимися. - Длительность радиоимпульса равна времени установления колебаний — полоса пропускания контура оптимальная (рис. 19.11, в) выполняется соотношение (19.17). В этом случае колебания в контуре могут считаться установившимися к моменту окончания воздействия. Такое же время
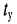 потребуется на затухание колебаний в контуре до величины, равной
потребуется на затухание колебаний в контуре до величины, равной 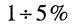 от установившегося значения. Следовательно, через время
от установившегося значения. Следовательно, через время 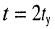 с момента начала воздействия контур будет готов к приёму очередного радиоимпульса.
с момента начала воздействия контур будет готов к приёму очередного радиоимпульса. - Длительность радиоимпульса больше времени установления колебаний:
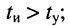 в этом случае установление колебаний и затухание происходят быстрее (рис. 19.11, г), поэтому очередной радиоимпульс может быть подан на колебательный контур через время
в этом случае установление колебаний и затухание происходят быстрее (рис. 19.11, г), поэтому очередной радиоимпульс может быть подан на колебательный контур через время 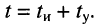
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Расчет переходных процессов
- Классический метод расчета переходных процессов
- Анализ переходных и установившихся процессов методом интеграла свертки
- Операторный метод расчета переходных процессов
- Переходные процессы
- Переходные процессы в линейных цепях
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами