Параллелограмм, его свойства и признаки с примерами решения

Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.

На рисунке 16 изображен параллелограмм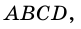

Рассмотрим свойства параллелограмма.

1. Сумма двух любых соседних углов параллелограмма равна 180°.

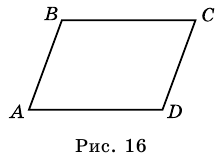
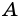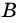Действительно, углы  и параллелограмма 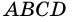(рис. 16) являются внутренними односторонними углами для параллельных прямых 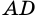и 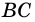и секущей 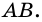Поэтому 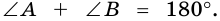Аналогично это свойство можно доказать для любой другой пары соседних углов параллелограмма. 

2. Параллелограмм является выпуклым четырехугольником.

Так как 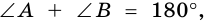то 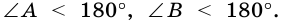Аналогично  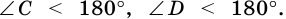Поэтому параллелограмм - выпуклый четырехугольник. 

3. В параллелограмме противолежащие стороны равны и противолежащие углы равны.

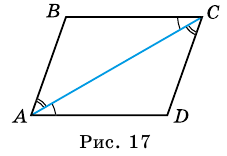
Доказательство:

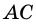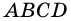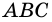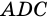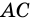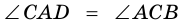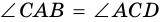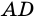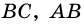Диагональ разбивает параллелограмм на два треугольника и (рис. 17). -их общая сторона, и (как внутренние накрест лежащие углы для каждой из пар параллельных прямых  и и 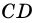и секущей 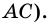Тогда 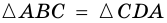(по стороне и двум прилежащим углам). Откуда, 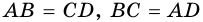и 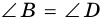(как соответственные элементы равных треугольников). Так как 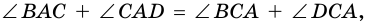то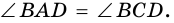  

4. Периметр параллелограмма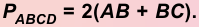

5. Диагонали параллелограмма точкой пересечения делятся пополам.

Доказательство:

Пусть 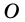- точка пересечения диагонале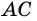й и 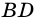параллелограмма 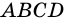(рис. 18). 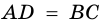(как противолежащие стороны параллелограмма), 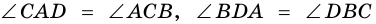(как внутренние накрест лежащие углы для параллельных прямых 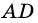и 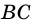и секущих 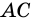и 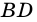соответственно). Следовательно, 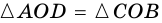(по стороне и двум прилежащим углам). Тогда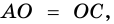 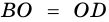  (как соответственные стороны равных треугольников). 

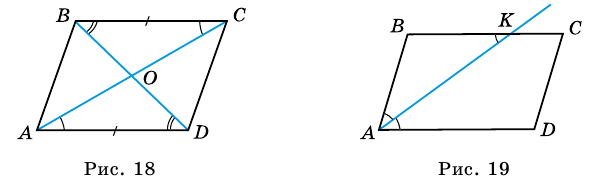
Пример:

Дано: 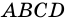параллелограмм, 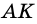- биссектриса угла 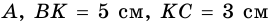(рис. 19). Найдите: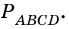

Решение:

1)

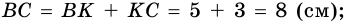
2) 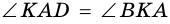 (как внутренние накрест лежащие углы для параллельных прямых 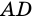и 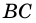и секущей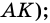

3) 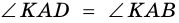 (по условию), тог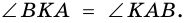да Тогда 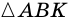- равнобедренный (по признаку равнобедренного треугольника),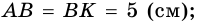

4) 

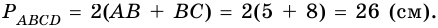
Ответ. 26 см.

Высотой параллелограмма называют перпендикуляр, проведенный из любой точки стороны параллелограмма к прямой, содержащей противолежащую сторону.

На рисунке 20 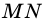- высота параллелограмма,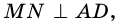

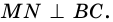
Из каждой вершины параллелограмма можно провести две высоты. Например, на рисунке 21 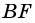и 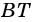- высоты параллелограмма, проведенные соответственно к сторонам 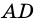и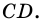

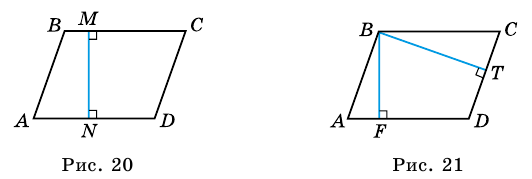
Рассмотрим признаки параллелограмма.

Теорема (признаки параллелограмма). Если в четырехугольнике: 1) две стороны параллельны и равны, или 2) противолежащие стороны попарно равны, или 3) диагонали точкой пересечения делятся пополам, или 4) противолежащие углы попарно равны, — то четырехугольник является параллелограммом.

Доказательство:

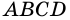
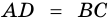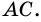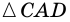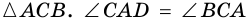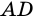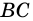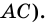
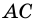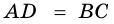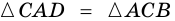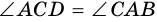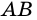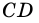1) Пусть в четырехугольнике   и (рис. 22). Проведем диагональ Рассмотрим и  (как внутренние накрест лежащие при параллельных прямых  и и секущей - общая сторона, (по условию). Следовательно, (по двум сторонам и углу между ними). Тогда (как соответственные). Но это накрест лежащие углы при пересечении прямых и секущей 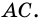Поэтому 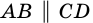(по признаку параллельности прямых). Следовательно, в четырехугольнике 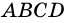противолежащие стороны попарно параллельны. Поэтому 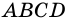-параллелограмм.

2) Пусть в четырехугольнике 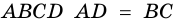и 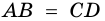(рис. 22). Проведем диагональ 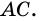Тогда 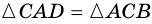(по трем сторонам). Поэтому 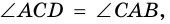и следовательно, 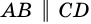(по признаку параллельности прямых). Аналогично доказываем, что 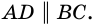Следовательно, 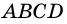- параллелограмм.

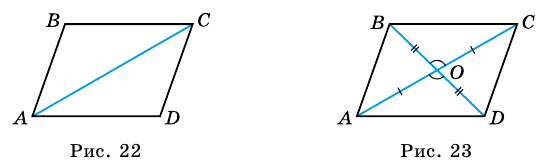
3) Пусть в четырехугольнике 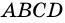диагонал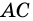и и 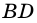пересекаются в точке 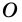и 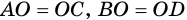(рис. 23). 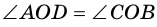(как вертикальные). Поэтому 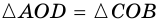(по двум сторонам и углу между ними). Отсюда 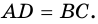Аналогично доказываем, что 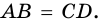Принимая во внимание п. 2) этой теоремы, приходим к выводу, что 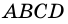- параллелограмм.

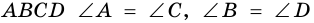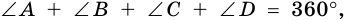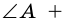
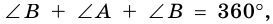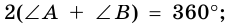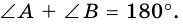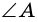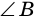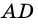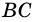4) Пусть в параллелограмме (рис. 16). Так как  то  т. е.  откуда Но и - внутренние накрест лежащие углы для прямых и и секущей 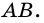Поэтому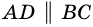

по признаку параллельности прямых). Аналогично доказываем, что 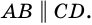Следовательно,  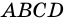- параллелограмм. 

Пример:

В четырехугольнике 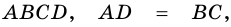 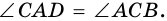Докажите, что 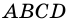- параллелограмм.

Доказательство:

Пусть 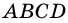- данный четырехугольник (рис. 22). Рассмотрим  и 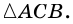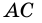- их общая сторона, 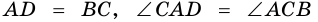(по условию). Тогда, 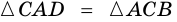(по двум сторонам и углу между ними). Следовательно, 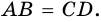Но тогда в четырехугольнике 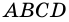противолежащие стороны попарно равны, поэтому он является параллелограммом. 

A еще раньше...

О некоторых видах четырехугольников (квадраты, прямоугольники, равнобокие и прямоугольные трапеции) знали еще древнеегипетские и вавилонские математики.

Термин «параллелограмм» греческого происхождения, считают, что он был введен Евклидом (около 300 г. до н. э.). Также известно, что еще раньше о параллелограмме и некоторых его свойствах уже знали ученики школы Пифагора («пифагорейцы»).

В «Началах» Евклида доказана следующая теорема: в параллелограмме противолежащие стороны равны и противолежащие углы равны, а диагональ делит его пополам, но не упоминается о том, что точка пересечения диагоналей параллелограмма делит каждую из них пополам.

Евклид также не упоминает ни о прямоугольнике, ни о ромбе.

Полная теория параллелограммов была разработана лишь в конце Средневековья, а в учебниках она появилась в XVII в. Все теоремы и свойства параллелограмма в этих учебниках основывались на аксиоме параллельности Евклида.

Термин «диагональ» - греческого происхождения; «диа» означает «через», а «гониос» - «угол», что можно понимать как отрезок, соединяющий вершины углов.

Следует отметить, что Евклид, как и большинство математиков того времени, для названия отрезка, соединяющего противолежащие вершины четырехугольника, в частности прямоугольника, употреблял другой термин - «диаметр». Это можно объяснить тем, что первые геометры свои рассуждения основывали на вписанных в окружность прямоугольниках. В Средние века для названия упомянутого отрезка использовали оба термина. Лишь в XVIII в. термин «диагональ» стал общепринятым.