
Параллельные силы в теоретической механике
Параллельные силы:
Силы называются параллельными, если параллельны линии их действия.
Рассмотрим сначала сложение двух параллельных сил 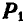
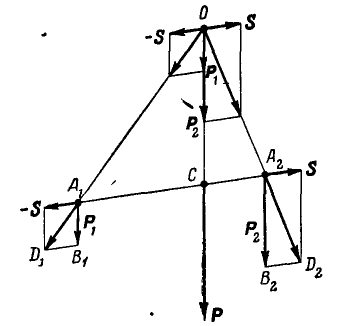
Рис. 34.
Складывая попарно силы 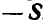 и
и 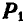 , а также
, а также 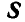 и
и 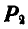 , получаем их равнодействующие, которые переносим в точку их схода О. Раскладывая вновь перенесенные равнодействующие, замечаем, что силы
, получаем их равнодействующие, которые переносим в точку их схода О. Раскладывая вновь перенесенные равнодействующие, замечаем, что силы 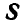 и
и 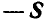 взаимно уравновешиваются, а силы
взаимно уравновешиваются, а силы 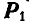 и
и 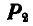 приводятся к одной равнодействующей
приводятся к одной равнодействующей 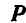 , которая по величине равна
, которая по величине равна 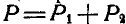 . Перенесем силу Р в точку С.
. Перенесем силу Р в точку С.
Для нахождения положения точки С рассмотрим подобные треугольники: 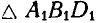 подобен
подобен 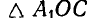 и
и 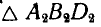 подобен
подобен 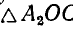 , окуда получаем соотношения:
, окуда получаем соотношения:
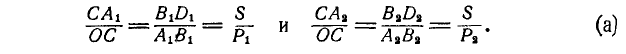
Деля первую пропорцию на вторую, имеем:
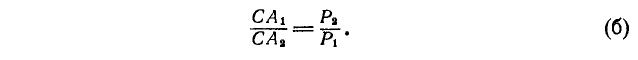
На основании свойств пропорции получим:
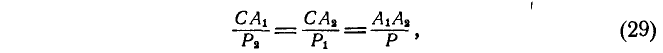
а также
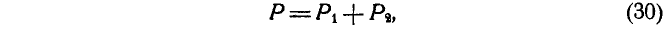
т. е. равнодействующая двух параллельных сил, направленных в одну сторону, параллельна им, направлена в ту же сторону и равна их сумме; ее направление делит внутренним образом расстояние между точками приложения составляющих на части, обратно пропорциональные составляющим силам.
Если имеются две неравные параллельные силы 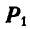 и
и 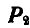 , направленные в противоположные стороны (рис. 35), то, предполагая, например, что
, направленные в противоположные стороны (рис. 35), то, предполагая, например, что 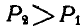 и, рассуждая аналогично предыдущему, получаем из рассмотрения подобных треугольников:
и, рассуждая аналогично предыдущему, получаем из рассмотрения подобных треугольников: 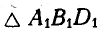 и
и  , а также
, а также  и
и  соотношения (а) и (б).
соотношения (а) и (б).
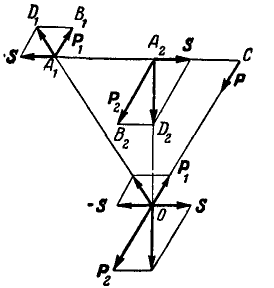
Рис. 35.
Из равенства (б), а также на основании свойств пропорции получим:
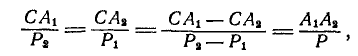
где равнодействующая данных сил 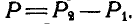
Отсюда следует, что равнодействующая двух параллельных сил, направленных в разные стороны, параллельна им, направлена в сторожу большей силы и равна их разности; точка приложения ее находится за большей силой и делит внешним образом расстояние между точками приложения составляющих на части, обратно пропорциональные составляющим силам.
Задача:
На тело (рис. 36) действуют две параллельные силы, причем известна одна из составляющих 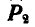 и их равнодействующая Р. Определить вторую составляющую силу
и их равнодействующая Р. Определить вторую составляющую силу 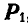 , если
, если 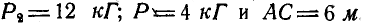 .
.
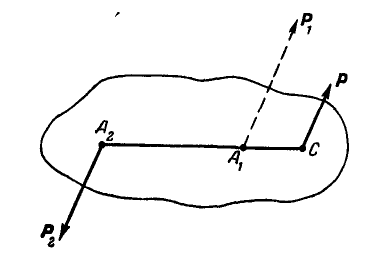
Рис. 36.
Решение:
Пусть 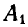 —точка приложения неизвестной нам силы
—точка приложения неизвестной нам силы 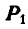 ; тогда ее величину и точку приложения найдем из уравнений:
; тогда ее величину и точку приложения найдем из уравнений: 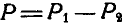 или
или 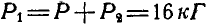 . Далее,
. Далее, 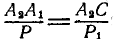 ; отсюда
; отсюда 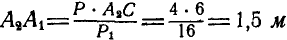 .
.
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |