
Параллельность в пространстве с примерами решения
Содержание:
Параллельность в пространстве
В этом параграфе вы ознакомитесь с основными понятиями стереометрии, аксиомами стереометрии и следствиями из них. Расширите свои представления о многогранниках. Вы узнаете о взаимном расположении двух прямых, прямой и плоскости, двух плоскостей в пространстве. Ознакомитесь с правилами, по которым изображают пространственные фигуры на плоскости.
Основные понятия стереометрии. Аксиомы стереометрии
Изучая математику, вы со многими понятиями ознакомились с помощью определений. Так, из курса планиметрии вам хорошо знакомы определения четырехугольника, трапеции, окружности и др.
Определение любого понятия основано на других понятиях, содержание которых вам уже известно. Например, рассмотрим определение трапеции: «Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны». Видим, что определение трапеции основано на таких уже введенных понятиях, как четырехугольник, сторона четырехугольника, параллельные и непараллельные стороны и др. Итак, определения вводятся по принципу «новое основано на старом». Тогда ясно, что должны существовать первоначальные понятия, которым определений не дают. Их называют основными понятиями (рис. 27.1).
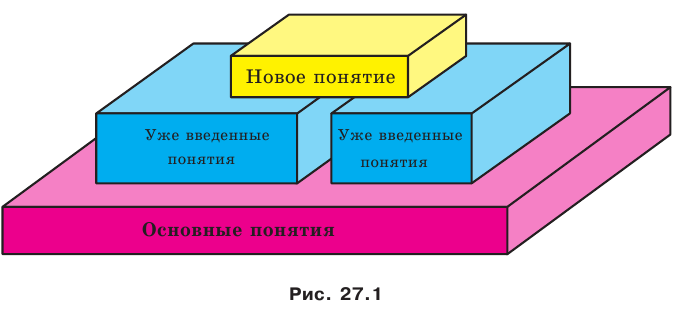
В изученном вами курсе планиметрии определения не давали таким фигурам, как точка и прямая. В стереометрии, кроме них, к основным понятиям отнесем еще одну фигуру — плоскость.
Наглядное представление о плоскости дают поверхность водоема в безветренную погоду, поверхность зеркала, поверхность полированного стола, мысленно продолженные во всех направлениях.
Используя понятие плоскости, можно считать, что в планиметрии мы рассматривали только одну плоскость, и все изучаемые фигуры принадлежали этой плоскости. В стереометрии же рассматривают бесконечно много плоскостей, расположенных в пространстве.
Как правило, плоскости обозначают строчными греческими буквами 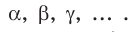
Плоскость, так же как и прямая, состоит из точек, то есть плоскость — это множество точек.
Существует несколько случаев взаимного расположения точек, прямых и плоскостей в пространстве. Приведем примеры.
На рисунке 27.4 изображена точка А, принадлежащая плоскости 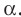 . Также говорят, что точка А лежит в плоскости
. Также говорят, что точка А лежит в плоскости 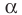 или плоскость
или плоскость 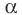 проходит через точку А. Кратко это можно записать так:
проходит через точку А. Кратко это можно записать так: 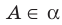 .
.
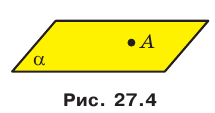
На рисунке 27.5 изображена точка В, не принадлежащая плоскости 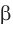 . Кратко это можно записать так:
. Кратко это можно записать так: 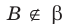 .
.
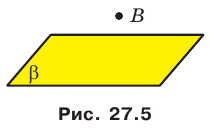
На рисунке 27.6 изображена прямая 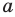 , принадлежащая плоскости
, принадлежащая плоскости 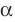 . Также говорят, что прямая
. Также говорят, что прямая 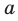 лежит в плоскости
лежит в плоскости 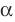 или плоскость
или плоскость 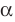 проходит через прямую
проходит через прямую 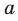 . Кратко это можно записать так:
. Кратко это можно записать так: 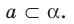
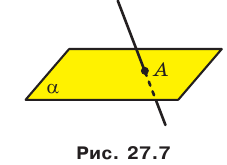
Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость. На рисунке 27.7 изображена прямая 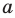 , пересекающая плоскость
, пересекающая плоскость 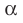 в точке А. Записывают:
в точке А. Записывают: 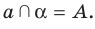
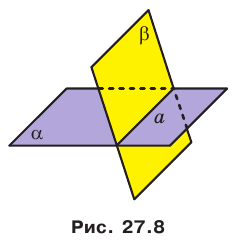
В дальнейшем, говоря «две точки», «три точки», «две плоскости» и т.п., будем иметь в виду, что это разные точки, разные прямые и разные плоскости. Если две плоскости имеют общую точку, то говорят, что эти плоскости пересекаются.
На рисунке 27.8 изображены плоскости 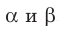 , пересекающиеся по прямой
, пересекающиеся по прямой 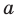 . Записывают:
. Записывают: 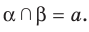
На начальном этапе изучения стереометрии невозможно доказывать теоремы, опираясь на другие утверждения, поскольку этих утверждений еще нет. Поэтому первые свойства, касающиеся точек, прямых и плоскостей в пространстве, принимают без доказательства и называют аксиомами. Отметим, что ряд аксиом стереометрии по формулировкам дословно совпадают со знакомыми вам аксиомами планиметрии.
Например:
- какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей;
- через любые две точки можно провести прямую, и притом только одну.
Мы не будем знакомиться со строгим аксиоматическим построением стереометрии. Рассмотрим лишь некоторые утверждения, выражающие основные свойства плоскостей пространства, основываясь на которых обычно строят курс стереометрии в школе.
Аксиома А1. В любой плоскости пространства выполняются все аксиомы планиметрии.
Если в любой плоскости пространства выполняются аксиомы планиметрии, то выполняются и следствия из этих аксиом, то есть теоремы планиметрии. Следовательно, в стереометрии можно пользоваться всеми известными нам свойствами плоских фигур.
Аксиома А2. Через любые три точки пространства, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Рисунки 27.9-27.11 иллюстрируют эту аксиому.



Из этой аксиомы следует, что три точки пространства, не лежащие на одной прямой, определяют единственную плоскость, про ходящую через эти точки. Поэтому для обозначения плоскости можно указать любые три ее точки, не лежащие на одной прямой.
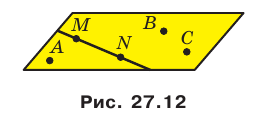
Например, на рисунке 27.12 изображена плоскость АВС. Запись 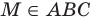 означает, что точка М принадлежит плоскости АВС. Запись
означает, что точка М принадлежит плоскости АВС. Запись 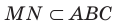 означает, что прямая MN принадлежит плоскости АВС (рис. 27.12).
означает, что прямая MN принадлежит плоскости АВС (рис. 27.12).
Аксиома АЗ. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
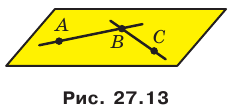
Например, на рисунке 27.13 точки А, В и С принадлежат плоскости АВС. Тогда можно записать: 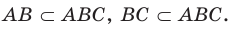 Из этой аксиомы следует, что если прямая не принадлежит плоскости, то она имеет с данной плоскостью не более одной общей точки.
Из этой аксиомы следует, что если прямая не принадлежит плоскости, то она имеет с данной плоскостью не более одной общей точки.
Утверждение, сформулированное в аксиоме АЗ, часто используют на практике, когда хотят проверить, является ли данная поверхность ровной (плоской). Для этого к поверхности в разных местах прикладывают ровную рейку и проверяют, есть ли зазор между рейкой и поверхностью (рис. 27.14).
Аксиома А4. Если две плоскости имеют общую точку, то они пересекаются по прямой.
Эту аксиому можно проиллюстрировать с помощью согнутого листа бумаги или с помощью вашего учебника (рис. 27.15).


Пример:
Докажите, что если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Решение:
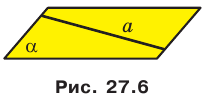
Пусть точка А является общей для двух плоскостей 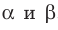 , то есть
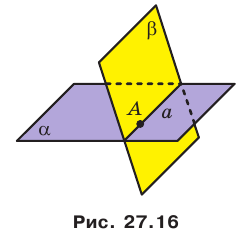
, то есть 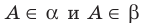 (рис. 27.16). По аксиоме А4 плоскости
(рис. 27.16). По аксиоме А4 плоскости 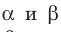 пересекаются по прямой. Пусть
пересекаются по прямой. Пусть 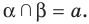 Тогда все общие точки плоскостей
Тогда все общие точки плоскостей 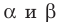 принадлежат прямой
принадлежат прямой 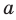 . Точка А является общей для плоскостей
. Точка А является общей для плоскостей 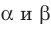 . Следовательно,
. Следовательно,  Кроме аксиом, есть и другие свойства, описывающие взаимное расположение точек, прямых и плоскостей в пространстве. Опираясь на аксиомы, можно доказать, например, следующие утверждения (следствия из аксиом стереометрии).
Кроме аксиом, есть и другие свойства, описывающие взаимное расположение точек, прямых и плоскостей в пространстве. Опираясь на аксиомы, можно доказать, например, следующие утверждения (следствия из аксиом стереометрии).
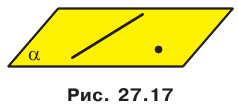
Теорема 27.1. Через прямую и не принадлежащую ей точку проходит плоскость, и притом только одна (рис. 27.17).
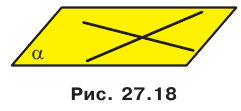
Теорема 27.2. Через две пересекающиеся прямые проходит плоскость, и притом только одна (рис. 27.18).
Из аксиомы А2 и теорем 27.1 и 27.2 следует, что плоскость однозначно определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, не принадлежащей этой прямой;
- двумя пересекающимися прямыми.
Таким образом, мы указали три способа задания плоскости.
Пространственные фигуры
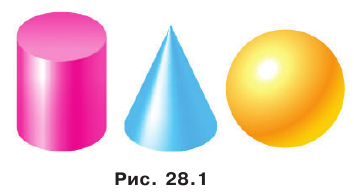
Начальные сведения о многогранниках. В стереометрии, кроме точек, прямых и плоскостей, рассматривают пространственные фигуры, то есть фигуры, не все точки которых лежат в одной плоскости. Некоторые из пространственных фигур вам уже знакомы. Так, на рисунке 28.1 изображены цилиндр, конус и шар. Подробно эти фигуры вы будете изучать в 11 классе.
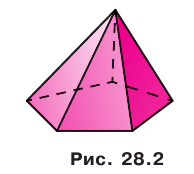
На рисунке 28.2 изображена еще одна знакомая вам пространственная фигура — пирамида. Эта фигура является частным видом многогранника. Примеры многогранников показаны на рисунке 28.3.

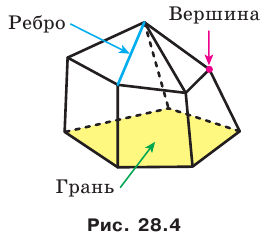
Поверхность многогранника состоит из многоугольников. Их называют гранями многогранника. Стороны многоугольников называют ребрами многогранника, а вершины — вершинами многогранника (рис. 28.4).
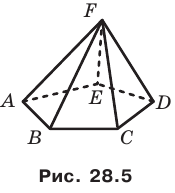
На рисунке 28.5 изображена пятиугольная пирамида FABCDE.
Поверхность этого многогранника состоит из пяти треугольников, которые называют боковыми гранями пирамиды, и одного пятиугольника, который называют основанием пирамиды. Вершину F, общую для всех боковых граней, называют вершиной пирамиды.
Ребра FA, FB, FC, FD и FE называют боковыми ребрами пирамиды, а ребра А В, ВС, CD, DE и ЕА — ребрами основания пирамиды.
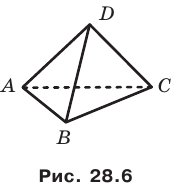
На рисунке 28.6 изображена треугольная пирамида DABC. Треугольную пирамиду называют также тетраэдром.
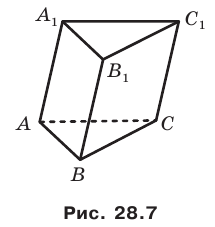
Еще одним частным видом многогранника является призма. На рисунке 28.7 изображена треугольная призма 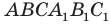 . Этот многогранник имеет пять граней, две из которых — равные треугольники АВС и
. Этот многогранник имеет пять граней, две из которых — равные треугольники АВС и 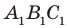 Их называют основаниями призмы.
Их называют основаниями призмы.
Остальные грани призмы — параллелограммы. Их называют боковыми гранями призмы. Ребра 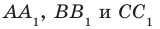 называют боковыми ребрами призмы.
называют боковыми ребрами призмы.
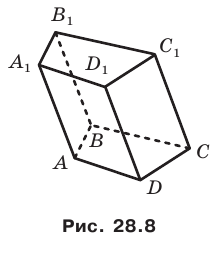
На рисунке 28.8 изображена четырехугольная призма 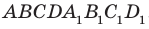 . Ее поверхность состоит из двух равных четырехугольников ABCD и
. Ее поверхность состоит из двух равных четырехугольников ABCD и 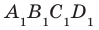 (основания призмы) и четырех параллелограммов (боковые грани призмы).
(основания призмы) и четырех параллелограммов (боковые грани призмы).
Вы знакомы также с частным видом четырехугольной призмы — прямоугольным параллелепипедом. На рисунке 28.9 изображен прямоугольный параллелепипед 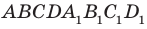 . Все грани прямоугольного параллелепипеда являются прямоугольниками.
. Все грани прямоугольного параллелепипеда являются прямоугольниками.
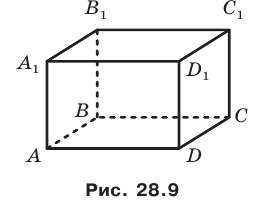
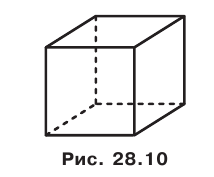
В свою очередь, частным видом прямоугольного параллелепипеда является куб. Все грани куба — равные квадраты (рис. 28.10).
Четырехугольную призму, основанием которой является параллелограмм, называют параллелепипедом.
В курсе геометрии 11 класса вы более подробно ознакомитесь с многогранниками и их частными видами.
Пример:
На ребрах 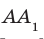 и
и 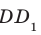 куба
куба 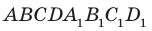 отметили соответственно точки М и N так, что
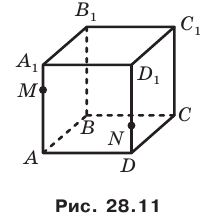
отметили соответственно точки М и N так, что 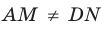 (рис. 28.11). Постройте точку пересечения прямой MN с плоскостью АВС.
(рис. 28.11). Постройте точку пересечения прямой MN с плоскостью АВС.
Решение:
Точки М и N принадлежат плоскости 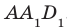 . Тогда по аксиоме АЗ прямая MN принадлежит этой плоскости. Аналогично прямая AD также принадлежит плоскости
. Тогда по аксиоме АЗ прямая MN принадлежит этой плоскости. Аналогично прямая AD также принадлежит плоскости 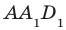 . Из планиметрии известно, что прямые, лежащие в одной плоскости, или параллельны, или пересекаются. Поскольку
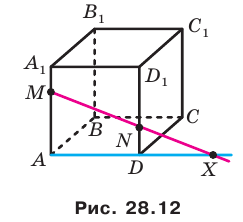
. Из планиметрии известно, что прямые, лежащие в одной плоскости, или параллельны, или пересекаются. Поскольку 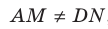 , то прямые AD и MN пересекаются. Пусть X — точка их пересечения (рис. 28.12). Точки А и D принадлежат плоскости АВС. Тогда по аксиоме АЗ прямая AD принадлежит этой же плоскости. Точка X принадлежит прямой AD. Следовательно, точка X принадлежит плоскости АВС. Поскольку точка X также принадлежит прямой MN, то прямая MN пересекает плоскость АВС в точке X.
, то прямые AD и MN пересекаются. Пусть X — точка их пересечения (рис. 28.12). Точки А и D принадлежат плоскости АВС. Тогда по аксиоме АЗ прямая AD принадлежит этой же плоскости. Точка X принадлежит прямой AD. Следовательно, точка X принадлежит плоскости АВС. Поскольку точка X также принадлежит прямой MN, то прямая MN пересекает плоскость АВС в точке X.
Взаимное расположение двух прямых в пространстве
Из курса планиметрии вы знаете, что две прямые называют пересекающимися, если они имеют только одну общую точку. Такое же определение пересекающихся прямых дают и в стереометрии. Вам также известно, что две прямые называют параллельными, если они не пересекаются. Можно ли это определение перенести в стереометрию?
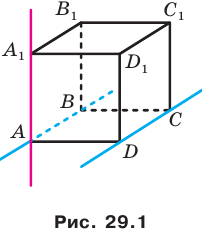
Обратимся к рисунку 29.1, на котором изображен куб 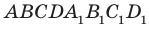 . Каждая из прямых АВ и
. Каждая из прямых АВ и 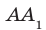 не имеет с прямой DC общих точек. При этом прямые АВ и DC лежат в одной плоскости — в плоскости АВС, а прямые
не имеет с прямой DC общих точек. При этом прямые АВ и DC лежат в одной плоскости — в плоскости АВС, а прямые 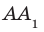 и DC не лежат в одной плоскости, то есть не существует плоскости, которая проходила бы через эти прямые. Этот пример показывает, что в стереометрии для двух прямых, не имеющих общих точек, возможны два случая взаимного расположения: прямые лежат в одной плоскости и прямые не лежат в одной плоскости. Для каждого из этих случаев дадим соответствующее определение.
и DC не лежат в одной плоскости, то есть не существует плоскости, которая проходила бы через эти прямые. Этот пример показывает, что в стереометрии для двух прямых, не имеющих общих точек, возможны два случая взаимного расположения: прямые лежат в одной плоскости и прямые не лежат в одной плоскости. Для каждого из этих случаев дадим соответствующее определение.
Определение. Две прямые в пространстве называют параллельным и, если они лежат в одной плоскости и не пересекаются. Если прямые 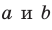 параллельны, то записывают:
параллельны, то записывают: 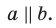
Определение. Две прямые в пространстве называют скрещивающимися, если они не лежат в одной плоскости. Например, на рисунке 29.1 прямые АВ и DC — параллельные, а прямые 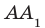 и DC — скрещивающиеся.
и DC — скрещивающиеся.

Наглядное представление о параллельных прямых дают колонны здания, корабельный лес, бревна сруба (рис. 29.2).

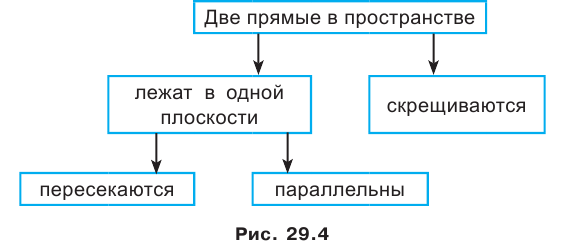
Наглядное представление о скрещивающихся прямых дают провода линий электропередачи, различные элементы строительных конструкций (рис. 29.3). Итак, существуют три возможных случая взаимного расположения двух прямых в пространстве (рис. 29.4):
- прямые пересекаются;
- прямые параллельны;
- прямые скрещиваются.
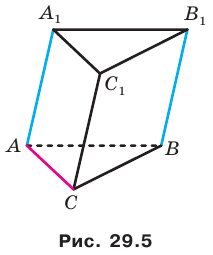
Два отрезка называют параллельными (скрещивающимися), если они лежат на параллельных (скрещивающихся) прямых. Например, ребра 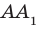 и
и 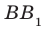 треугольной призмы
треугольной призмы 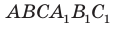 (рис. 29.5) являются параллельными, а ребра АС и
(рис. 29.5) являются параллельными, а ребра АС и 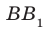 — скрещивающимися.
— скрещивающимися.
Теорема 29.1. Через две параллельные прямые проходит плоскость, и притом только одна.
Доказательство. Пусть даны параллельные прямые 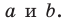 Докажем, что существует единственная плоскость
Докажем, что существует единственная плоскость 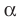 такая, что
такая, что 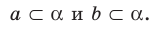
Существование плоскости 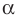 , проходящей через прямые
, проходящей через прямые 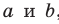 , следует из определения параллельных прямых.
, следует из определения параллельных прямых.
Если предположить, что существует еще одна плоскость, проходящая через прямые 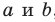 , то через прямую а и некоторую точку прямой
, то через прямую а и некоторую точку прямой 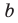 будут проходить две различные плоскости, что противоречит теореме 27.1.
будут проходить две различные плоскости, что противоречит теореме 27.1.
Существует три способа задания плоскости. Теорему 29.1 можно рассматривать как еще один способ задания плоскости — с помощью двух параллельных прямых.
Установить параллельность двух прямых, лежащих в одной плоскости, можно с помощью известных вам из курса планиметрии признаков параллельности двух прямых. А как установить, являются ли две прямые скрещивающимися? Ответить на этот вопрос позволяет следующая теорема.
Теорема 29.2 (признак скрещивающихся прямых). Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые — скрещивающиеся (рис. 29.6).
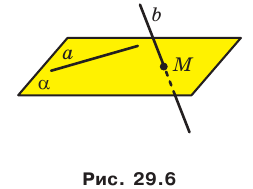
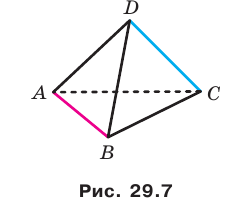
На рисунке 29.7 ребра АВ и DC тетраэдра DABC являются скрещивающимися. Действительно, прямая DC пересекает плоскость АВС в точке С, не принадлежащей прямой АВ. Следовательно, по признаку скрещивающихся прямых прямые АВ и DC являются скрещивающимися.
Параллельность прямой и плоскости
Вам уже известны два возможных случая взаимного расположения прямой и плоскости:
- прямая принадлежит плоскости, то есть все точки прямой принадлежат плоскости;
- прямая пересекает плоскость, то есть прямая имеет с плоскостью только одну общую точку.
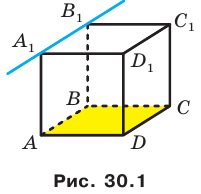
Понятно, что возможен и третий случай, когда прямая и плоскость не имеют общих точек. Например, прямая, содержащая ребро 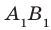 куба
куба 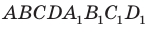 , не имеет общих точек с плоскостью АВС (рис. 30.1).
, не имеет общих точек с плоскостью АВС (рис. 30.1).
Определение. Прямую и плоскость называют параллельными, если они не имеют общих точек.
Если прямая 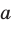 и плоскость
и плоскость 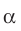 параллельны, то записывают:
параллельны, то записывают: 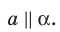 Также принято говорить, что прямая
Также принято говорить, что прямая 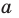 параллельна плоскости
параллельна плоскости 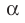 , а плоскость
, а плоскость 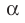 параллельна прямой
параллельна прямой 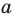 .
.
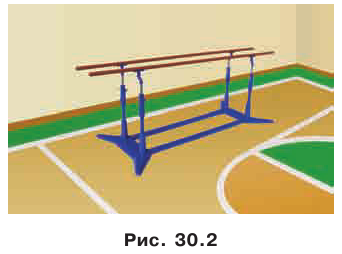
Наглядное представление о прямой, параллельной плоскости, дают некоторые спортивные снаряды. Например, брусья параллельны плоскости пола (рис. 30.2). Другой пример — водосточная труба: она параллельна плоскости стены (рис. 30.3).

Выяснять, параллельны ли данные прямая и плоскость, с помощью определения затруднительно. Гораздо эффективнее пользоваться следующей теоремой.
Теорема 30.1 (признак параллельности прямой и плоскости). Если прямая, не принадлежащая данной плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости.
Например, на рисунке 30.1 прямые 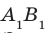 и
и 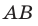 содержат противолежащие стороны квадрата
содержат противолежащие стороны квадрата 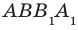 . Эти прямые параллельны.
. Эти прямые параллельны.
Поскольку 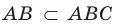 , то по признаку параллельности прямой и плоскости
, то по признаку параллельности прямой и плоскости 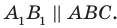
Отрезок называют параллельным плоскости, если он принадлежит прямой, параллельной этой плоскости. Например, ребро АВ куба параллельно плоскости 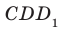 (рис. 30.1).
(рис. 30.1).
Вы умеете устанавливать параллельность двух прямых с помощью теорем-признаков, известных из планиметрии. Рассмотрим теоремы, описывающие достаточные условия параллельности двух прямых в пространстве.
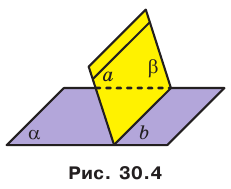
Теорема 30.2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то прямая пересечения плоскостей параллельна данной прямой.
На рисунке 30.4 прямая 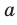 параллельна плоскости
параллельна плоскости 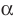 . Плоскость
. Плоскость 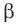 проходит через прямую
проходит через прямую 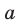 и пересекает плоскость
и пересекает плоскость 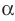 по прямой
по прямой 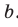 . Тогда
. Тогда 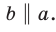
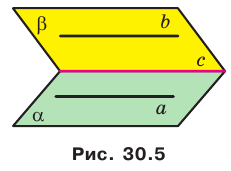
Теорема 30.3. Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются по прямой, отличной от двух данных, то эта прямая параллельна каждой из двух данных прямых.
На рисунке 30.5 прямые 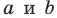 параллельны, плоскость
параллельны, плоскость 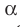 проходит через прямую
проходит через прямую 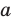 , а плоскость
, а плоскость 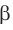 — через прямую
— через прямую 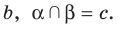 Тогда
Тогда 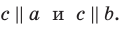
Теорема 30.4. Две прямые, параллельные третьей прямой, параллельны между собой.
Пример:
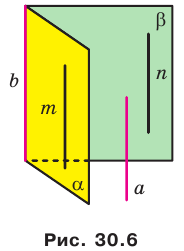
Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна прямой их пересечения.
Решение:
Пусть даны прямая 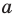 и плоскости
и плоскости 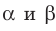 такие, что
такие, что 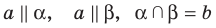 (рис. 30.6). Докажем, что
(рис. 30.6). Докажем, что 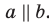 В плоскостях
В плоскостях 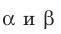 найдутся соответственно такие прямые
найдутся соответственно такие прямые 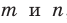 , что
, что 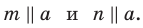 Если хотя бы одна из прямых
Если хотя бы одна из прямых 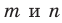 совпадает с прямой
совпадает с прямой 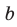 , то утверждение задачи доказано. Если же каждая из прямых
, то утверждение задачи доказано. Если же каждая из прямых 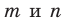 отлична от прямой
отлична от прямой 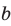 , то по теореме 30.4
, то по теореме 30.4 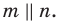 Воспользовавшись теоремой 30.3, приходим к выводу, что
Воспользовавшись теоремой 30.3, приходим к выводу, что 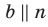 . Но
. Но 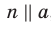 , следовательно,
, следовательно, 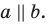
Параллельность плоскостей
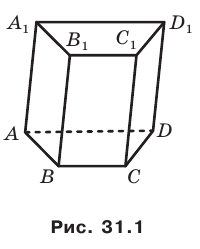
Рассмотрим варианты возможного взаимного расположения двух плоскостей. Вы знаете, что две плоскости могут иметь общие точки, то есть пересекаться. Понятно, что две плоскости могут и не иметь общих точек. Например, плоскости АВС и  , содержащие основания призмы, не имеют общих точек (рис. 31.1).
, содержащие основания призмы, не имеют общих точек (рис. 31.1).
Определение. Две плоскости называют параллельны ми, если они не имеют общих точек.
Если плоскости 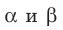 параллельны, то записывают:
параллельны, то записывают: 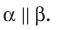 Также принято говорить, что плоскость
Также принято говорить, что плоскость 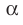 параллельна плоскости
параллельна плоскости 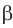 или плоскость
или плоскость 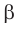 параллельна плоскости
параллельна плоскости 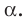
Наглядное представление о параллельных плоскостях дают потолок и пол комнаты; поверхность воды, налитой в аквариум, и его дно (рис. 31.2).

Из определения параллельных плоскостей следует, что любая прямая, лежащая в одной из двух параллельных плоскостей, параллельна другой плоскости.
В тех случаях, когда надо выяснить, являются ли две плоскости параллельными, удобно пользоваться следующей теоремой.
Теорема 31.1 (признак параллельности двух плоскостей). Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то эти плоскости параллельны.
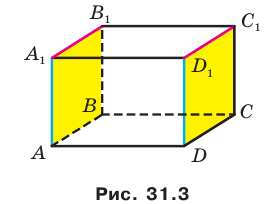
Например, на рисунке 31.3 изображен прямоугольный параллелепипед 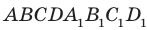 . Имеем:
. Имеем: 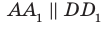 и
и 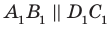 . Тогда по признаку параллельности двух плоскостей
. Тогда по признаку параллельности двух плоскостей 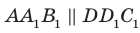 .
.
Будем говорить, что два многоугольника параллельны, если они лежат в параллельных плоскостях. Например, грани 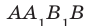 и
и 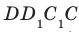 прямоугольного параллелепипеда
прямоугольного параллелепипеда 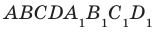 параллельны (рис. 31.3). Рассмотрим некоторые свойства параллельных плоскостей.
параллельны (рис. 31.3). Рассмотрим некоторые свойства параллельных плоскостей.
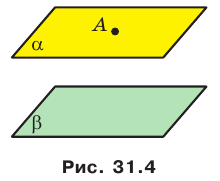
Теорема 31.2. Через точку в пространстве, не принадлежащую данной плоскости, проходит плоскость, параллельная данной плоскости, и притом только одна (рис. 31.4).
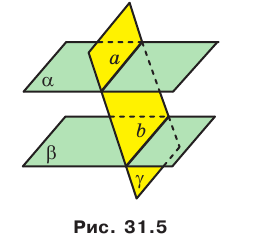
Теорема 31.3. Прямые пересечения двух параллельных плоскостей третьей плоскостью параллельны (рис. 31.5).
Пример:
Докажите, что отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Решение:
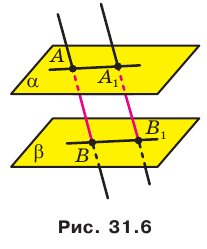
Пусть даны параллельные плоскости 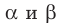 и параллельные прямые АВ и
и параллельные прямые АВ и 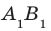 такие, что
такие, что 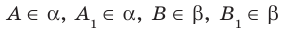 (рис. 31.6). Докажем, что
(рис. 31.6). Докажем, что 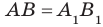 . Параллельные прямые АВ и
. Параллельные прямые АВ и 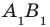 задают некоторую плоскость
задают некоторую плоскость 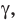 причем
причем 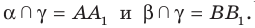
По теореме 31.3 получаем: 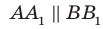 . Следовательно, четырехугольник
. Следовательно, четырехугольник 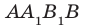 — параллелограмм. Отсюда
— параллелограмм. Отсюда 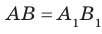 .
.
Параллельное проектирование
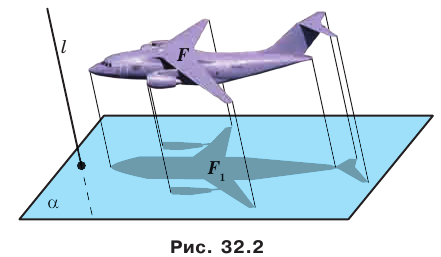
Многие явления и процессы, наблюдаемые нами в повседневной жизни, служат примерами преобразований, при которых образом пространственной фигуры является плоская фигура. Увидеть одно из таких явлений можно в солнечную погоду, когда предмет отбрасывает тень на плоскую поверхность (рис. 32.1). Этот пример иллюстрирует преобразование фигуры, которое называют параллельным проектированием. С помощью этого преобразования на плоскости создают изображения пространственных фигур.

Многие рисунки настоящего учебника, на которых изображены пространственные фигуры, можно рассматривать как тени, отбрасываемые на плоскость страницы предметами, освещенными параллельными лучами. Ознакомимся подробнее с параллельным проектированием.
Пусть даны плоскость 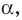 прямая
прямая 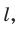 пересекающая эту плоскость, и фигура F (рис. 32.2). Через каждую точку фигуры F проведем прямую, параллельную прямой
пересекающая эту плоскость, и фигура F (рис. 32.2). Через каждую точку фигуры F проведем прямую, параллельную прямой 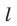 (если точка фигуры F принадлежит прямой
(если точка фигуры F принадлежит прямой 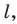 то будем рассматривать саму прямую
то будем рассматривать саму прямую 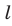 ). Точки пересечения всех проведенных прямых с плоскостью
). Точки пересечения всех проведенных прямых с плоскостью 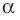 образуют некоторую фигуру
образуют некоторую фигуру 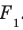 . Описанное преобразование фигуры F называют параллельным проектированием. Фигуру
. Описанное преобразование фигуры F называют параллельным проектированием. Фигуру 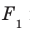 называют параллельной проекцией фигуры F на плоскость
называют параллельной проекцией фигуры F на плоскость 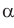 в направлении прямой
в направлении прямой 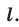 Также фигуру
Также фигуру 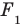 называют изображением фигуры
называют изображением фигуры 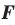 на плоскости
на плоскости 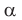 в направлении прямой
в направлении прямой 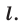
Выбирая выгодные положения плоскости 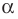 и прямой
и прямой 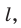 можно получить наглядное изображение данной фигуры F. Это связано с тем, что параллельное проектирование обладает рядом замечательных свойств (см. теоремы 32.1-32.3). Благодаря этим свойствам изображение фигуры похоже на саму фигуру.
можно получить наглядное изображение данной фигуры F. Это связано с тем, что параллельное проектирование обладает рядом замечательных свойств (см. теоремы 32.1-32.3). Благодаря этим свойствам изображение фигуры похоже на саму фигуру.
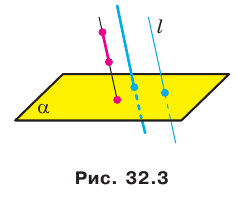
Пусть даны плоскость 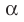 и прямая
и прямая 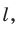 пересекающая эту плоскость. Если прямая параллельна прямой
пересекающая эту плоскость. Если прямая параллельна прямой 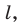 то ее проекцией на плоскость
то ее проекцией на плоскость 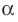 является точка (рис. 32.3). Проекцией прямой
является точка (рис. 32.3). Проекцией прямой 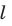 также является точка. Если отрезок параллелен прямой
также является точка. Если отрезок параллелен прямой 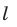 или лежит на прямой
или лежит на прямой 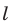 , то его проекцией на плоскость
, то его проекцией на плоскость 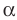 является точка (рис. 32.3).
является точка (рис. 32.3).
В следующих теоремах будем рассматривать прямые и отрезки, не параллельные прямой 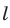 и не лежащие на ней.
и не лежащие на ней.
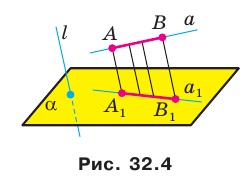
Теорема 32.1. Параллельной проекцией прямой является прямая; параллельной проекцией отрезка является отрезок (рис. 32.4).
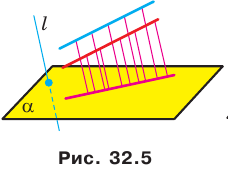
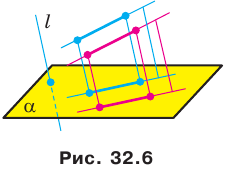
Теорема 32.2. Параллельной проекцией двух параллельных прямых являются или прямая (рис. 32.5), или две параллельные прямые (рис. 32.6). Параллельные проекции двух параллельных отрезков лежат на одной прямой или на параллельных прямых (рис. 32.6).
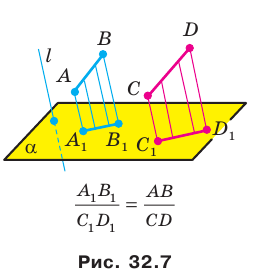
Теорема 32.3. Отношение параллельных проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению самих отрезков (рис. 32.7).
Рассмотрим изображения некоторых многоугольников на плоскости 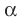 в направлении прямой
в направлении прямой 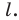
Если прямая 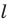 параллельна плоскости многоугольника или принадлежит этой плоскости, то изображением многоугольника является отрезок. Теперь рассмотрим случай, когда прямая
параллельна плоскости многоугольника или принадлежит этой плоскости, то изображением многоугольника является отрезок. Теперь рассмотрим случай, когда прямая 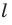 пересекает плоскость многоугольника.
пересекает плоскость многоугольника.
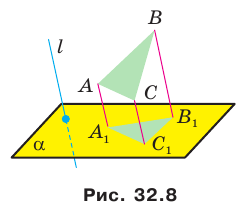
Из свойств параллельного проектирования следует, что параллельной проекцией треугольника является треугольник (рис. 32.8).
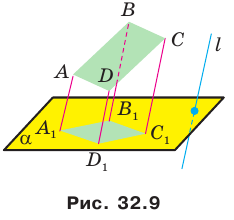
Поскольку при параллельном проектировании сохраняется параллельность отрезков, то изображением параллелограмма (в частности, прямоугольника, ромба, квадрата) является параллелограмм (рис. 32.9).
Также из свойств параллельного проектирования следует, что изображением трапеции является трапеция.
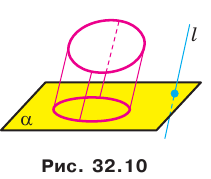
Параллельной проекцией окружности является фигура, которую называют эллипсом (рис. 32.10).
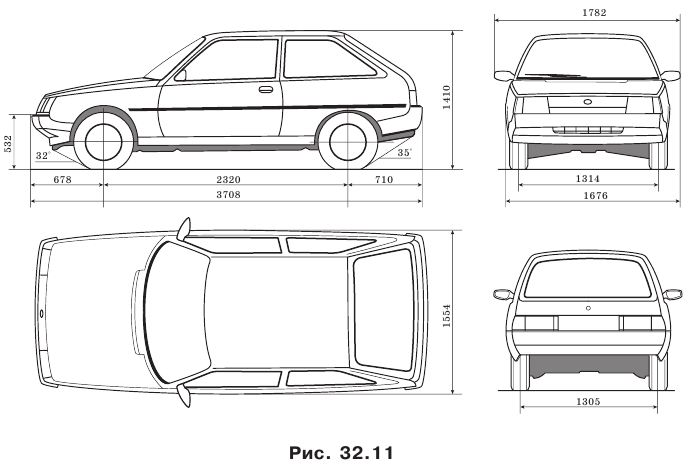
Изображения объектов с помощью параллельного проектирования широко используют в самых разных областях промышленности, например в автомобилестроении (рис. 32.11).
 ГЛАВНОЕ В ПАРАГРАФЕ 4
ГЛАВНОЕ В ПАРАГРАФЕ 4
Основные аксиомы стереометрии
- А1. В любой плоскости пространства выполняются все аксиомы планиметрии.
- А2. Через любые три точки пространства, не лежащие на одной прямой, проходит плоскость, и притом только одна.
- АЗ. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
- А4. Если две плоскости имеют общую точку, то они пересекаются по прямой.
Плоскость однозначно определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, не принадлежащей этой прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми.
Взаимное расположение двух прямых в пространстве
- Две прямые называют пересекающимися, если они имеют только одну общую точку.
- Две прямые в пространстве называют параллельными, если они лежат в одной плоскости и не пересекаются.
- Две прямые в пространстве называют скрещивающимися, если они не лежат в одной плоскости.
Свойство параллельных прямых
Через две параллельные прямые проходит плоскость, и притом только одна.
Признак скрещивающихся прямых
Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые — скрещивающиеся.
Параллельность в пространстве
Прямую и плоскость называют параллельными, если они не имеют общих точек. Две плоскости называют параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости
Если прямая, не принадлежащая данной плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости.
Условия параллельности двух прямых в пространстве
- Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то прямая пересечения плоскостей параллельна данной прямой.
- Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются по прямой, от личной от двух данных, то эта прямая параллельна каждой из двух данных прямых.
- Две прямые, параллельные третьей прямой, параллельны между собой.
Признак параллельности двух плоскостей
Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то эти плоскости параллельны.
Свойства параллельных плоскостей
Через точку в пространстве, не принадлежащую данной плоскости, проходит плоскость, параллельная данной плоскости, и притом только одна.
Прямые пересечения двух параллельных плоскостей третьей плоскостью параллельны.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |