Парадокс Браеса - пример и изучение

Содержание:

Парадокс Браеса - это парадокс, приписываемый немецкому математику Дитриху Браеса (статья 1968 г.). В нем говорится, что добавление дополнительной емкости в сеть, предполагая, что объекты, перемещающиеся по сети, выбирают свой собственный маршрут, может снизить общую производительность. Причина в том, что равновесие Нэша не обязательно является оптимальным для таких систем.

Парадокс можно проиллюстрировать на примере дорожной сети. Предположим, у нас есть заданная дорожная сеть, для каждого из ее узлов мы знаем количество автомобилей, вылетающих из нее, и пункты назначения этих автомобилей. Одна дорога может быть предпочтительнее другой не только из-за качества покрытия, но и потому, что оно менее перегружено. Если каждый водитель выберет наиболее удобный для него маршрут, то полученное время в пути не обязательно будет минимальным. Более того, можно привести пример, когда перераспределение трафика в ответ на создание дополнительных дорог приводит лишь к увеличению времени в пути.

Парадокс Браеса в реальной жизни

В реальной жизни примеры парадокса Брееса в Штутгарте ссылаются на улучшение дорожной ситуации после того, как участок новой дороги закрыт для движения. В 1990 году закрытие 42-й улицы в Нью-Йорке уменьшило заторы на этой территории.

Математик Алексей Савватеев утверждает, что парадокс Брееса обычно не длится долго: Дорожные службы исправляют ситуацию всего через несколько месяцев. Рядом со своим домом, в Метрогородке, он поймал такой пример: проезд по Щелковскому шоссе - проспекту ветеранов занимает 1 час. Лесная тропа, ведущая из Метрогородки на проспект Ветерана, занимает 20 минут. До Щелковского шоссе 10 минут (сейчас асфальтированная дорога). Пропускная способность и той, и другой на порядок меньше, чем у шоссе, а небольшой процент автомобилей, которые хотят проехать по грунтовым дорогам, абсолютно не рельефная дорога, но из-за них жители Метрогородка оказались в 30-минутной пробке (1 ч - 10 - 20 = 30).

Парадокс Браеса

Парадокс Браеса был выведен немецким математиком Дитрихом Браесом (Dietrich Braes) в 1968 году и гласит, что добавление в сеть большего количества энергии при условии, что движущиеся в сети объекты определяют свой собственный маршрут, может привести к снижению общей мощности. Это связано с тем, что равновесие Нэша не всегда оптимально в таких системах.

Примером парадокса является дорожная сеть. Пусть будет указана дорожная сеть, количество автомобилей для каждого узла, отъезжающего от нее, и пункт назначения этих автомобилей. Некоторые дороги могут быть предпочтительнее других не только потому, что качество их дорожного покрытия лучше, но и потому, что у них самая низкая плотность движения. Когда водители выбирают наиболее удобные для них маршруты, время в пути может быть не минимальным. Есть также примеры, когда перераспределение трафика путем создания дополнительных дорог не сокращает время в пути.

Ярким примером Braes Paradox в реальной жизни является улучшение движения в Штутгарте после того, как был закрыт участок новой дороги. А закрытие 42-й улицы в Нью-Йорке в 1990 году уменьшило пробки в этом районе.

Пример парадокса Браеса

Рассмотрим еще один пример парадокса Браеса (Рисунок 1). Предположим, что автомобилисты хотят ехать из точки "Старт" в точку "Конец". Существует два маршрута - через точку А и через точку Б. Время пути от пункта отправления до точки A зависит от плотности движения автомобилей и равно количеству автомобилей (T), деленному на 100. Время пути от пункта отправления до точки B не зависит от количества автомобилей и равно 45 минутам. По аналогии, время в пути от А до конца занимает 45 минут, а время в пути от В до пункта назначения равно Т/100. Если А и В не соединены, то время в пути через пункт А равно А/100+45, а через пункт В-100+45. Если маршрут короче, то равновесия Нэша нет, и все рациональные водители переключились бы на более короткий маршрут. Предположим, что 4000 автомобилей покинули стартовую точку, то в соответствии с тем, что A + B = 4000, система установит равновесие при A = B = 2000. Таким образом, независимо от выбранной дороги, автомобили будут ездить 2000 / 100 + 45 = 65 минут.

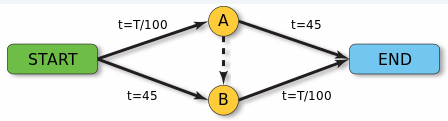
Рисунок 1: Пример парадокса Брэса 1. 

Рассмотрим пример, когда пунктирная линия, соединяющая А и В, является новой дорогой, по которой ехать примерно 40 минут. В данной ситуации все водители предпочтут маршрут через пункт А, так как этот маршрут занимает T/100 = 4000 / 100 = 40 минут даже в худшем случае, в то время как маршрут через пункт В гарантированно займет 45 минут. В пункте А все разумные водители предпочтут проехать по более короткому маршруту до пункта В, а затем доехать до конца, так как в худшем случае маршрут А - В - конец составляет всего 0 + 4000 / 100 = 40 минут. Из этого следует, что время в пути каждого водителя равно 4000 / 100 + 4000 / 100 = 80 минут, т.е. после открытия новой дороги время в пути увеличится на 15 минут.

Если водители согласятся не пользоваться дорогами А и В, они выиграют время. Однако, поскольку каждый водитель пытается сэкономить время, используя дорогу A-B, такое распределение не кажется социально оптимальным. Это проявление парадокса Браеса.

Изучение парадокса Браеса методами экспериментальной экономики

Важнейшей задачей многих исследователей сегодня является поиск решений транспортных проблем крупных городов. Решением этой проблемы может быть:

• Уменьшение количества транспортных средств;
• Открытие платных дорог;
• расширение шоссе;
• строить новые дороги.

Однако каждое решение может привести не только к положительным, но и к отрицательным результатам. Оказалось, что строительство новых дорог также может оказать негативное влияние на стоимость транспортных потоков. Это нашло свое выражение в парадоксе Брейза.

Проблемы транспорта могут быть изучены различными методами с использованием графика, ориентированного на транспортную сеть. Рассмотрим один такой пример. Предположим, что загрузка сети равна 6 тыс. абонентов в час. Абонентам необходимо попасть из точки 1 в точку 4 по одному из двух путей, показанных на рисунке 2. Требуемая стоимость, т.е. вес кромки, указывается на ней, а y(ij) - число автомобилистов, путешествующих по данной кромке. Все участники дорожного движения стараются минимизировать свои издержки, поэтому равновесие Нэша в данной ситуации заключается в том, чтобы разделить потоки на равные части по двум путям. Таким образом, x(124) = x(134) = 3, x(1k4) - это число участников, выбравших путь k, а общее время в пути - 83 минуты. Строительство новой дополнительной дороги от пункта 3 до пункта 2 увеличивает время в пути, если потоки распределены равномерно. Открытие третьей дороги приводит к равновесному распределению, которое составляет x(124) = x (134) = x(1324) = 2, и общая стоимость должна уменьшиться, но время в пути составит 92 минуты. Из рассмотренной ситуации можно сделать вывод, что открытие дополнительной дороги создаст единое равновесие Нэша, которое не является оптимальным для Парето, это парадокс Браеса.

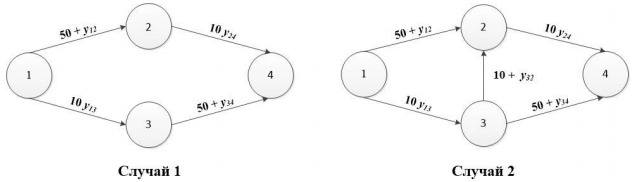
Рисунок 2: Пример парадокса Браеса 2. 

Для изучения парадокса Браеса на практике Лаборатория экспериментальной экономики провела игры со студентами. Это было сделано с помощью программы, основанной на z-деревой оболочке, которая реплицирует типы транспортных сетей. В эксперименте участвовали 6 человек, задача которых состояла в том, чтобы выбрать один из двух путей в одном случае и один из трех в другом. В симметричном случае игроки относительно быстро пришли в равновесие, которое было оптимальным по Парето. В ситуации с дополнительным путем участники выбрали Парето-неоптимальный исход, демонстрируя парадокс Браеса.