Парадокс Бертрана - равновесие, сущность и решение

Содержание:

Модель Бертрана, или конкуренция Бертрана, - это модель ценовой конкуренции на олигополистическом рынке, сформулированная французским математиком и экономистом Жозефом Бертраном в 1883 году.

Модель описывает поведение фирм на олигополистическом рынке, которые конкурируют, изменяя цены на свою продукцию. Парадоксальный вывод модели - фирмы будут взимать цену, равную их предельной стоимости, как это делают фирмы, когда они идеально конкурентоспособны - известен как Bertrand Paradox.

Модель делает следующие предположения:

• На рынке существует, по крайней мере, две фирмы, которые производят однородный продукт;
• фирмы ведут себя некооперативно;
• Предельные расходы (ПЗ) фирм равны и постоянны;
• Функция спроса является линейной;
• Фирмы конкурируют, устанавливая цену на свою продукцию и выбирая цену самостоятельно и одновременно;
• После выбора цены фирмы производят количество товара, равное спросу на их продукцию;
• Когда цены отличаются, потребители требуют более дешевый товар;
• При одинаковых ценах товары всех фирм закупаются в равных количествах.
• Модель является статической (рассматривает принятие решений в один момент времени).

Предположение о ценовой конкуренции означает, что фирмы могут легко менять выпуск продукции, но после выбора очень трудно или невозможно изменить цену.

Равновесие в классической модели Бертрана

В соответствии с моделью Cournot, фирмы выбирают уровни выхода и оставляют определение цены на рынке. Согласно другому подходу, фирмы оценивают свою продукцию и оставляют ее на рынке для определения количества проданных товаров. Эта модель известна как конкурс Бертранда. Французский экономист Жозеф Бертран представил свою модель в обзоре работ Курно.

При выборе цены фирма должна предвидеть цену, установленную другой фирмой в отрасли. В ситуации, когда фирмы продают идентичные продукты, структура равновесия Бертранда на самом деле очень проста. Это равновесие оказывается конкурентным в той точке, когда цена равняется предельной стоимости. Цена никогда не может быть меньше предельной стоимости, в противном случае каждая фирма увеличит свою прибыль, производя меньше. Поэтому рассмотрим случай, когда цена выше предельной стоимости. Если фирма 1 снижает свою цену на произвольно малую величину, а фирма 2 поддерживает свою цену, то все потребители захотят купить товар фирмы 1. Снижая свою цену на произвольно малое количество, фирма 2 может переманить всех своих клиентов.

Если фирма 1 действительно считает, что фирма 2 будет взимать более высокую цену, чем ее предельная стоимость, она всегда будет делать все возможное, чтобы снизить свою цену. Но фирма 2 может спорить так же. Следовательно, в равновесии не может быть цены выше предельной стоимости; единственное возможное равновесие - это конкурентное равновесие.

Если рассматривать модель Бертрана как конкурентоспособную, то такой результат имеет больший смысл. Предположим, что одна фирма подала заявку по цене выше ее предельной стоимости. Тогда другая фирма всегда может получить прибыль, понизив эту цену. Таким образом, единственная цена, на которую ни одна из фирм не может рассчитывать - это цена, равная ее предельной стоимости.

Сущность парадокса Бертрана

Некоторые вероятностные проблемы требуют геометрического подхода, например, поражение цели пистолетом. В таких задачах предполагается, что все случайные точки равномерно распределены по области. Степень вероятности попадания в любую часть этой области пропорциональна площади, т.е. объему или длине. Из-за таких вероятностей возникает ряд парадоксов. Например, вероятность попадания в центр цели равна нулю. С другой стороны, можно попасть и в эту точку. Из этого следует, что необходимо различать события, которые происходят с нулевой вероятностью, и невозможные события.

Парадокс Бертрана - это проблема классического определения теории вероятностей. Й. Бертранд описал этот парадокс в своей работе как пример того, что невозможно однозначно определить вероятность, если не выбран метод или механизм для определения случайной величины.

Для заданного круга случайным образом выбирается аккорд. Необходимо определить вероятность того, что данный аккорд длиннее, чем сторона правого треугольника, вписанного в круг. Согласно парадоксу, эта вероятность определяется неоднозначно, так как разные методы дают разные результаты. Бертран рассмотрел три метода решения, которые описаны ниже (рис. 1).

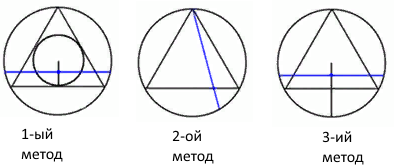
Рисунок 1: Методы решения в парадоксе Бертрана. 

Первый метод. Точка окружности выбирается случайным образом. Эта точка определяет единственный аккорд, для которого она является центром. Этот аккорд длиннее, чем сторона правого треугольника, если и только если его центр лежит в пределах круга, вписанного в треугольник. Радиус такой окружности равен 1/2 радиуса исходной окружности, поэтому площадь вписанной окружности равна 1/4 площади исходной окружности. Из этого следует, что вероятность нахождения случайно выбранной точки в пределах круга составляет 1/4.

Второй метод. Из соображений симметрии предположим, что один конец аккорда является фиксированной произвольной точкой на окружности. Предположим, что такая точка - это вершина треугольника, вписанного в окружность. Другой конец аккорда выбирается случайным образом. Вершины треугольника делят окружность на три одинаковые дуги, и случайный путь будет длиннее стороны треугольника только в том случае, если он пересекает данный треугольник. Таким образом, требуемая вероятность составляет 1/3.

Третий метод. Точка на радиусе окружности выбирается равномерно случайным образом, а хорда располагается перпендикулярно заданному радиусу и проходит через точку, которую мы определили. В этом случае случайная связка длиннее, чем сторона треугольника, вписанного в окружность, если случайная точка находится на половине радиуса, который ближе к центру. Из соображений симметрии не имеет значения, какой радиус выбран для конструкции, а требуемая вероятность составляет 1/2.

С одной стороны, аргументация верна во всех трех рассмотренных случаях, но вероятность одного и того же события различна. Это объясняется тем, что были рассмотрены три совершенно разные проблемы, т.е. в трех случаях мера была установлена по-разному:

• В первом методе мерой количества была площадь, на которой располагались рассматриваемые точки, и было рассчитано соотношение этих двух площадей.
• Во втором методе мерой количества было количество точек, попадающих под заданный угол, с использованием значения соответствующего угла, и вычислялось соотношение двух углов.
• В третьем методе, с другой стороны, хорда "двигалась" по диаметру, и, рассматривая отрезок как меру набора точек на нем, рассчитывалось соотношение длин этих отрезков.

Парадокс Бертрана в экономике

В торговле и экономике парадокс Бертранда описывает ситуацию, в которой два игрока достигают равновесия Нэша. Другими словами, две фирмы устанавливают цену, равную предельной стоимости.

В основе парадокса Бертранда лежит предпосылка, что в таких моделях, как модель конкуренции Курно, увеличение числа фирм связано с тем, что цены приближаются к величине предельной стоимости. В этих моделях парадокс Бертранда существует в олигополии небольшого числа фирм, получающих положительную прибыль, устанавливая цены выше себестоимости.

Например, две фирмы А и В продают однородную продукцию, каждая из которых имеет одинаковую стоимость производства и распределения. Таким образом, покупатели предпочитают тот или иной продукт только из-за его стоимости. Это означает, что спрос будет бесконечно эластичным по стоимости. Ни фирма "А", ни фирма "Б" не будут устанавливать более высокие расходы, чем другие, так как это приведет к нарушению парадокса Бертранда.

В парадоксе Бертранда может быть и дополнительное равновесие со смешанной стратегией и положительной экономической прибылью, если сумма монополии бесконечна. Если прибыль конечна, то положительная прибыль невозможна из-за ценовой конкуренции.

В реальной жизни парадокс Бертранда довольно редкий, так как продукты обычно отличаются не только ценой. Фирмы имеют ограничения на собственную способность производить и распространять продукцию. Поэтому две аналогичные фирмы редко имеют одинаковую стоимость.

Классическое решение и решение Джейнса

Классическое решение зависит от способа выбора аккорда. Только когда метод выбора зафиксирован, проблема имеет четко определенное решение. Методы выбора не уникальны, поэтому нет единого решения. Три решения, представленные Бертрандом, соответствуют различным методам выбора, а отсутствие дополнительных данных не является основанием для выбора метода.

Э. Янес предложил в своей работе метод решения парадокса Бертранда, основанный на принципе неопределенности: Необязательно использовать данные, которые не заданы условием. Джейнс отметил, что в задаче Бертрана не указано положение или размер круга, поэтому он утверждал, что в этом случае все объективные и точные решения не должны зависеть от размера и положения.