Парадокс Алле - теория, сущность и эксперимент

Содержание:

Измерение и суждение одинаково важны при принятии решений в условиях неопределенности. Разумные люди пытаются объективно оценить информацию: Если их прогнозы оказываются ошибочными, то они являются случайными ошибками, а не результатом стойкой предрасположенности к оптимизму или пессимизму. Эти люди воспринимают новую информацию в соответствии с четким перечнем приоритетов. Они знают, чего хотят, и используют информацию для выполнения своих желаний.

Предпочтения определяют, что что-то более желательное, чем что-то другое - борьба приоритетов заложена в самой концепции. Это полезная идея, но метод измерения предпочтений должен сделать его более ощутимым. Речь идет о понятии полезности как меры предпочтения - вычислить, насколько мы предпочитаем одно, а не другое. Мир полон желанных вещей, но разные люди готовы платить за них разные цены. И чем больше у нас чего-то есть, тем меньше мы склонны платить, чтобы получить больше.

Ожидаемая теория полезности

В экономике, теории игр, теории решений, теории ожидаемой полезности - помогает оценить полезность товара с точностью положительного аффинного преобразования с использованием неопределенности.

Ожидаемая теория полезности возникла как побочный продукт, дополнение к теории игр. Во втором издании своей книги (1947 г.) фон Нойман и Моргенштерн во вступительной главе, предшествующей описанию теории игр и ее применения в экономике, дают краткое описание основных положений экономической теории, которым они предлагают дать адекватный математический инструментарий, основанный на теории игр. Здесь, в этой вспомогательной главе к общей идее книги, добавленной только во втором издании, авторы излагают основные тезисы своей теории ожидаемой полезности. Фон Нойман и Моргенштерн отмечают, что понятие рационального поведения (максимизация полезности или прибыли), лежащее в основе экономической теории, недостаточно квантифицировано.

От обычного героя оригинальных маржиналистских моделей Робинсона "участники экономики социального обмена отличаются тем, что результат их действий зависит не только от них, но и от действий других". Каждый участник стремится к максимальному использованию функции..... не все его элементы находятся под его контролем". В ситуации с такой неопределенностью или риском трудно сформулировать критерий рационального поведения. Фон Нойман и Моргенштерн перешли от выбора между определенными исходами к выбору между лотереями с множественными неопределенными исходами и доказали, что критерием рациональности здесь может быть максимизация ожидаемой полезности: Рациональный экономический субъект должен выбрать вариант поведения (лотерея), имеющий максимальное значение переменной ? p,i(x,), где x - возможные исходы и их утилиты, и p. - их вероятности. Эта переменная называется ожидаемой утилитой.

Сущность Парадокса Аллеи

Парадокс Allee - это термин, относящийся к теории риска в экономике и теории принятия решений. Он назван в честь французского нобелевского лауреата по экономике М. Алле и основан на его работах.

Появление этого термина связано с публикацией статьи "Рациональное поведение человека перед лицом риска". Критика постулатов и аксиом американской школы".

Этот парадокс доказывает невозможность применения теории максимизации ожидаемой полезности в реальных условиях неопределенности и риска. Сущность парадокса правильно объяснена с математической точки зрения. Парадокс показывает, что реальные агенты, ведущие себя рационально, предпочтут достижение максимальной ожидаемой полезности достижению абсолютной надежности.

В 1952 году в Париже прошла конференция по экономическим рискам, в которой приняли участие самые известные экономисты того времени, впоследствии нобелевские лауреаты П. Самуэльсон, К. Эрроу, М. Фридман и др. Одним из главных организаторов этой конференции был М. Алле, который подготовил проблему отбора для аудитории. Он хотел доказать, что гости подвержены эффекту неопределенности, и в то же время критиковать теорию ожидаемой полезности и аксиому рационального выбора.

Другие примеры парадокса Аллеи

Другой пример парадокса Allee's Paradox - это выбор из следующих двух вариантов:

А) Гарантированные $99 со 100% вероятностью;
Б) 100 долларов с вероятностью 99%.
Средний выигрыш одинаков в обоих случаях:

99 x 100% = 99 = 99 = 100 x 99%.

Однако многочисленные эксперименты ясно доказывают следующее:

• Выбор вариантов A и B не является одинаковым;
• Большинство людей выбирают гарантии, т.е. вариант А.

За годы, прошедшие с момента открытия Alle's Paradox, было предложено большое количество решений, но все они были локальными, изолированными и противоречили другим проблемам и парадоксам, возникающим в связи с Alle's Paradox.

Парадокс Алле вызвал огромное количество не только теоретических, но и эмпирических исследований, а также ряд других парадоксов и проблем, которые не решались в течение многих лет. Это породило сомнения в способности экономической теории решать такие проблемы и парадоксы. В результате было оправданно ставить вопрос о рациональности человеческого выбора.

Главный герой экономической теории - человек. А парадокс Элея и связанные с ним проблемы и парадоксы вызывают сомнения в рациональности человека и, следовательно, в принципиальной возможности построения рациональной теории экономики.

Все люди, как правило, предпочитают безопасность риску, даже когда самый рискованный вариант выгоден. Психологи, изучавшие парадокс Алле, обнаружили, что люди вообще не рискуют. Когда вопрос формулируется с точки зрения прибыли и убытков, люди, скорее всего, сначала посмотрят на убытки и минимизируют их. Это явление называется отвращением к потерям.

Эксперимент в Алле

Сам Алли провел описанный ниже психологический эксперимент, который дал парадоксальные результаты. Человека просят выбрать одно решение и два в каждой паре рискованных решений.

В первом случае:

• Ситуация А. 100% уверенность в том, что будет выигрыш в 1 миллион франков;
• Ситуация B: 10% вероятность того, что будет прибыль в размере 5 млн. франков; 89% вероятность того, что будет прибыль в размере 1 млн. франков; 1% вероятность того, что ничего не будет.

Во втором случае человек должен выбрать ситуацию C или D:

• Ситуация С: Существует 10% вероятность выигрыша 5 миллионов франков и 90% вероятность проигрыша;
• Ситуация D: Вероятность выигрыша 1 млн. франков составляет 11%, вероятность проигрыша - 89%.

Allee обнаружила, что большое количество индивидуумов при данных условиях предпочитают ситуацию A в первой паре и ситуацию C во второй паре. Этот результат был парадоксальным. Согласно текущей гипотезе, человек, предпочитающий ситуацию A в первой паре, должен выбрать ситуацию D во второй паре, а человек, выбравший ситуацию B в первой паре, должен выбрать ситуацию C во второй паре. Все дали математически точное объяснение этому парадоксу. Его основная мысль заключается в том, что рациональные агенты предпочитают абсолютную надежность.

Проблема с этим парадоксом заключается в том, что математическое ожидание в первом случае составляет: A=1m, $B = 0.89 - 1 + 0.10 - 5 = $1.39m. В Си/Д ситуациях для 10% на 5m составляет $0.1 - 5 = $0.5m, а для 11% составляет $0.11 - 1 = $0.11m. Как показывают расчеты, нет ничего парадоксального в выборе варианта, который кажется самым дешевым даже без вычислений. И только после проведения расчетов можно увидеть, что 1% риск эквивалентен ожидаемой прибыли в 390 тыс. франков при выборе опционов B и C. Что в совокупности, когда цифры в 1% и 5 миллионов совпадают, кажется довольно парадоксальным. Другими словами, в первой ситуации 1% риска выбирается для убытков в 1 миллион, а во второй ситуации 1% риска выбирается для убытков в 1 миллион. Однако применение математического аппарата показывает, что в первой ситуации при 1% риске прибыль увеличивается в 1,39 раза, а во второй более чем в 4,5 раза.

С другой стороны, рассматриваемый парадокс можно сформулировать как выбор одного из двух вариантов, в каждом из которых существует определенная вероятность получения той или иной денежной суммы (рис. 1).

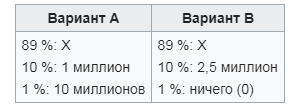
Рисунок 1: Парадокс Алле - два варианта.

На рисунке Х - это сумма, которую избиратель не знает. Вопрос в том, какой из двух вариантов будет более рациональным.

Математическое ожидание в первом случае:

$089X + 0,1 - 106 + 0,01 - 107 = 0,89X + 2,0 - $105

На секунду:

$0.89X + 0.1 - 2.5 - 106 + 0.01 - 0 = 0.89X + 2.5 - 105$

Таким образом, с математической точки зрения, второй вариант B является более выгодным, независимо от количества X. Однако люди боятся нулевого результата в варианте B, поэтому они с большей вероятностью выберут вариант А. Однако при X = 0 психологический барьер удаляется, и многие с большей вероятностью выберут вариант B.

Парадокс Аллеля - один из самых основных и известных парадоксов в экономической теории.