
Основные законы распределения вероятностей - определение и вычисление с примерами решения
Содержание:
В статистике наиболее часто применяются такие распределения:
- Нормальное (Гауссовское) распределение.
- Распределение Пирсона, распределение
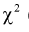
- Распределение Стьюдента (t - распределение).
- Распределение Фишера (F - распределение).
Нормальный закон распределения мы подробно рассмотрели при изучении раздела 6.5 теории вероятностей и здесь рассматриваться не будет.
Отметим, что в законы распределений математической статистики входит гамма-функция, поэтому необходимо познакомиться с этой функцией и рассмотреть ее свойства.
Гамма-функция и ее свойства
Гамма-функцией или интегралом Эйлера второго рода называется функция следующего вида:
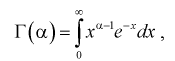
где  - параметр, от которого зависит значение интеграла.
- параметр, от которого зависит значение интеграла.
Свойства гамма-функции:
1. Г(1) = Г(2) = 1.
Доказательство:
Подставим 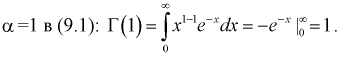
2. 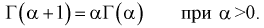
Доказательство:
Вычислим интеграл в (9.1), используя интегрирование по частям:
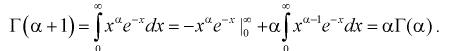
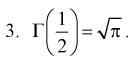
Доказательство:
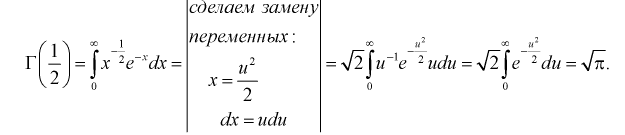
Значит, если значение 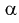 кратно
кратно 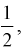 то
то 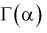 легко вычисляется с использованием свойства 2:
легко вычисляется с использованием свойства 2:
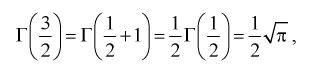
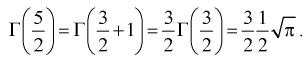
Для целых 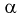 - гамма-функция это факториал:
- гамма-функция это факториал:
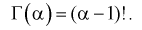
Например,
Г(3) = 2! = 2, Г(4) = 3! = 6, Г(5) = 4! = 24.
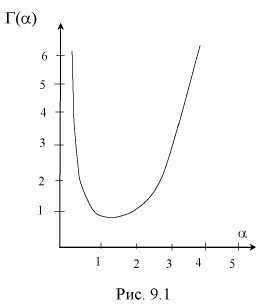
Отметим, что смысл гамма-функции - распространение понятия факториал на нецелые значения. На рис. 9.1 приведен график гамма-функции.
Распределение (хи-квадрат )
Распределение 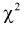 (хи-квадрат )
(хи-квадрат )
Случайная величина имеет закон распределения 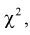 , если она определяется так:
, если она определяется так:
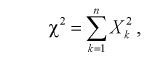 (9.2)
(9.2)
где 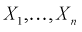 - независимые нормированные нормальные случайные величины, т. е.
- независимые нормированные нормальные случайные величины, т. е. 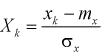 с плотностью распределения
с плотностью распределения 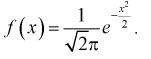
Распределение случайной величины, определенной по формуле (9.2), называется распределением Пирсона.
Покажем, что плотность распределения случайной величины  формула (9.2), определяется следующим равенством:
формула (9.2), определяется следующим равенством:
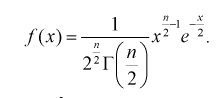 (9.3)
(9.3)
Здесь для краткости записи 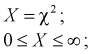
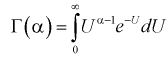 - гамма-функция,
- гамма-функция,
Для доказательства используем аппарат характеристических функций. Найдем характеристическую функцию случайной величины которая входит в формулу (9.2), учитывая, что  имеет нормированное нормальное распределение:
имеет нормированное нормальное распределение:
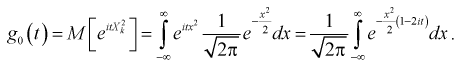
Используем подстановку 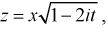 тогда
тогда
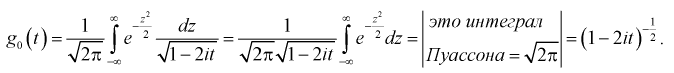
Согласно 5-му свойству характеристической функции (для суммы независимых случайных величин) найдем характеристическую функцию 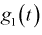 случайной величины
случайной величины 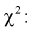
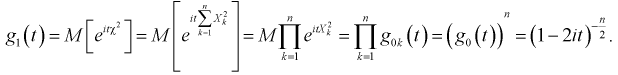
Найдем характеристическую функцию  случайной величины
случайной величины  плотность распределения которой определяется по формуле (9.3):
плотность распределения которой определяется по формуле (9.3):
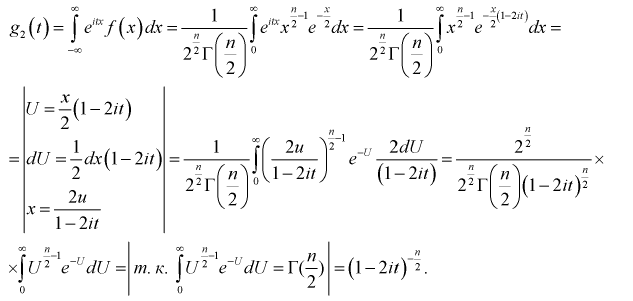
При сравнении правых частей характеристических функций 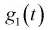 и
и 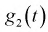 мы увидим, что они совпадают. Значит случайная величина, определяемая по формуле (9.2), действительно имеет плотность распределения вероятностей, определяемую формулой (9.3).
мы увидим, что они совпадают. Значит случайная величина, определяемая по формуле (9.2), действительно имеет плотность распределения вероятностей, определяемую формулой (9.3).
Найдем математическое ожидание и дисперсию случайной величины 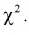
Продифференцируем 2 раза 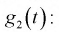
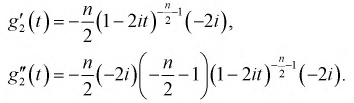
Значения производных при t = 0:
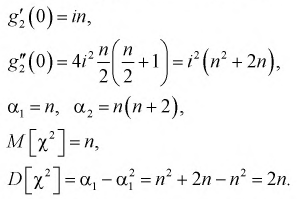
Таким образом, математическое ожидание  равно числу степеней свободы
равно числу степеней свободы  а дисперсия - удвоенному числу степеней свободы. Числом степеней свободы называется параметр
а дисперсия - удвоенному числу степеней свободы. Числом степеней свободы называется параметр 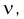 равный числу независимых случайных величин в (9.2) и который записывают
равный числу независимых случайных величин в (9.2) и который записывают 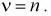
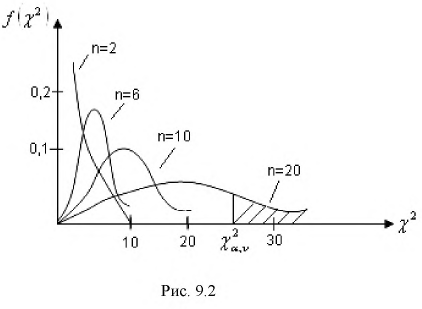
С ростом 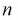 распределение становится симметричным относительно
распределение становится симметричным относительно 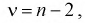 т. к. с увеличением
т. к. с увеличением 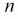 по центральной теореме закон распределения должен стремиться к нормальному закону (рис. 9.2).
по центральной теореме закон распределения должен стремиться к нормальному закону (рис. 9.2).
При 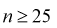 закон распределения
закон распределения 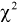 практически совпадает с нормальным законом.
практически совпадает с нормальным законом.
Квантилем 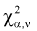 (где
(где 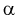 - заданный уровень вероятности,
- заданный уровень вероятности, 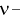 число степеней свободы) называется такое значение
число степеней свободы) называется такое значение 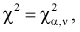 при котором
при котором
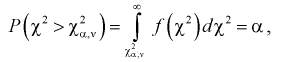 (9.4)
(9.4)
т. е. это то значение 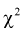 , при котором площадь заштрихованной фигуры на рис. 9.2 равна
, при котором площадь заштрихованной фигуры на рис. 9.2 равна 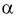 . Для определения квантилей
. Для определения квантилей 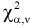 составлены таблицы хи-квадрат распределения. Чтобы воспользоваться ими, необходимо задать уровень вероятности
составлены таблицы хи-квадрат распределения. Чтобы воспользоваться ими, необходимо задать уровень вероятности 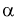 и число степеней свободы
и число степеней свободы 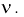
Распределение Стьюдента
Распределение Стьюдента 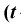 - распределение)
- распределение)
Случайная величина t имеет распределение Стьюдента, если она определяется так.
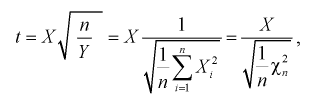 (9.5)
(9.5)
где X - нормированная нормальная случайная величина,
Y - величина 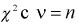 степенями свободы,
степенями свободы,
X и Y - независимые случайные величины.
Случайная величина t является функцией нормально распределенных нормированных случайных величин и называется безразмерной дробью Стьюдента. Плотность распределения случайной величины t определяется равенством
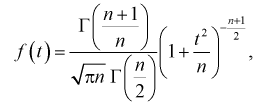 (9.6)
(9.6)
где 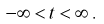
Числовые характеристики случайной величины t :
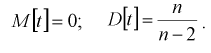
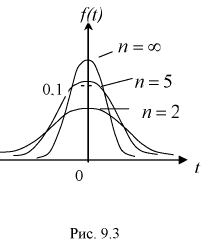
На рис. 9.3 приведены кривые распределения Стьюдента. Кривые на рис. 9.3 качественно напоминают кривые нормального закона распределения с математическим ожиданием, равным нулю, и при 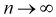 они стремятся к нормальному закону.
они стремятся к нормальному закону.
Квантили распределения Стьюдента 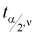 в зависимости от числа степеней
в зависимости от числа степеней 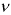 свободы и заданного уровня вероятности
свободы и заданного уровня вероятности 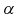 находятся из уравнения:
находятся из уравнения:
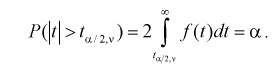
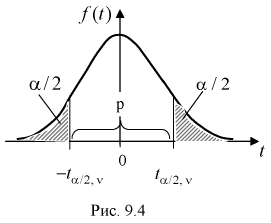
Рис. 9.4 иллюстрирует процесе определения квантилей, т. е. необходимо так выбрать 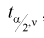 , чтобы суммарная площадь заштрихованных фигур была равна
, чтобы суммарная площадь заштрихованных фигур была равна 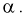
Распределение Фишера (F-распределение)
Случайная величина F имеет распределение Фишера, если она определяется так:
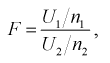 (9.7)
(9.7)
где 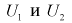 - независимые случайные величины, имеющие распределение
- независимые случайные величины, имеющие распределение 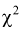 с
с 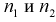 степенями свободы, т. е.
степенями свободы, т. е. 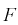 можно записать в следующем виде:
можно записать в следующем виде:
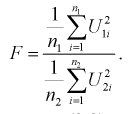 (9.8)
(9.8)
Безразмерная случайная величина F (9.8) имеет плотность распределения, определяемую следующей формулой:
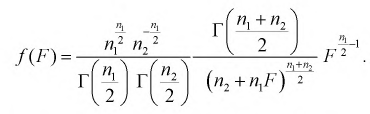 (9.9)
(9.9)
Распределение случайной величины F зависит от двух параметров 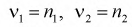 степеней свободы. График плотности распределения случайной величины F для разного числа степеней свободы приведен на рис. 9.5
степеней свободы. График плотности распределения случайной величины F для разного числа степеней свободы приведен на рис. 9.5
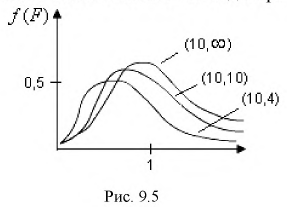
Квантили распределения Фишера 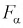 для заданного уровня вероятности
для заданного уровня вероятности 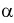 и числа степеней свободы
и числа степеней свободы 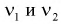 определяются из условия
определяются из условия
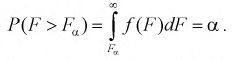
На рис. 9.6 показано, что надо так выбрать 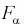 , чтобы площадь заштрихованной фигуры была равна заданной вероятности
, чтобы площадь заштрихованной фигуры была равна заданной вероятности 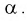
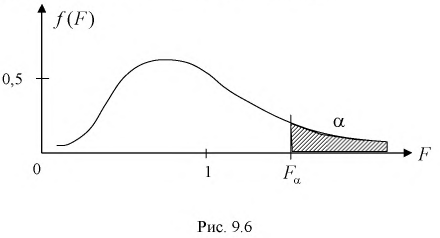
Как правило, квантили 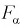 находят по таблицам распределения Фишера и для их определения необходимо задать три параметра: уровень вероятности
находят по таблицам распределения Фишера и для их определения необходимо задать три параметра: уровень вероятности 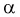 и число степеней свободы
и число степеней свободы 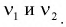
Биноминальный закон распределения
Определение: Дискретная случайная величина Х имеет биноминальный закон распределения, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями  где 0 < р < 1, q = 1 – p, m = 0, 1, …, n.
где 0 < р < 1, q = 1 – p, m = 0, 1, …, n.
Как видим, вероятности Р(Х = m) находятся по формуле Бернулли.
Следовательно, биноминальный закон распределения представляет собой закон распределения числа X = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.
Ряд распределения биноминального закона имеет вид: 
Теорема. Математическое ожидание случайной величины, распределенной по биноминальному закону  а ее дисперсия
а ее дисперсия 
Следствие. Математическое ожидание частости события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью, равно  а ее дисперсия
а ее дисперсия 
Биноминальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и в других областях.
Закон распределения Пуассона
Определение: Дискретная случайная величина Х имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, …, m с вероятностями  Ряд распределения закона Пуассона имеет вид:
Ряд распределения закона Пуассона имеет вид: 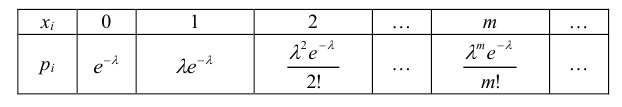
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е. 
При достаточно больших n (вообще при n → ∞) и малых значениях р (р → 0) при условии, что произведение np – постоянная величина (nр → λ = const), закон распределения Пуассона является хорошим приближением биноминального закона. Т.е. при n → ∞, р → 0, nр → λ = const закон распределения Пуассона является предельным случаем биноминального закона. Так как при этом вероятность р события А в каждом испытании мала, то закон распределения Пуассона часто называют законом редких явлений.
По закону Пуассона распределены, например, число сбоев на автоматической линии, число отказов сложной системы в нормальном режиме, число требований на обслуживание в единицу времени в системах массового обслуживания, и т.п.
Отметим еще, что если случайная величина представляет собой сумму двух независимых случайных величин, каждая из которых распределена по закону Пуассона, то она также распределена по закону Пуассона с параметром 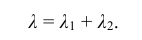
Равномерный закон распределения
Определение: Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a; b], если ее плотность вероятности f(x) постоянна на этом отрезке и равна нулю вне его, т.е. 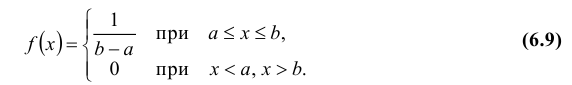
Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены соответственно на рис. 7.1 и рис. 7.2. 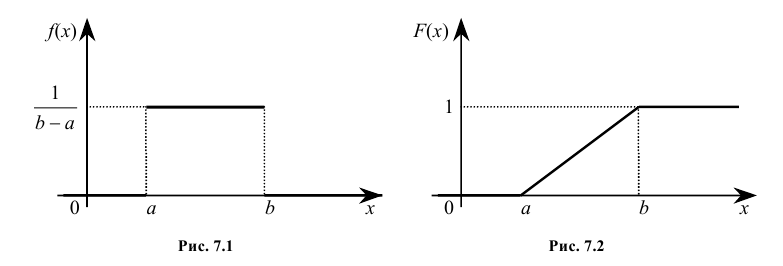
Теорема. Функция распределения случайной величины Х, распределенной по равномерному закону, есть 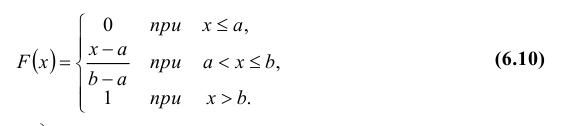

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач теории массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению, и т.д.
Показательный (экспоненциальный) закон распределения
Определение: Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности f(x) имеет вид: 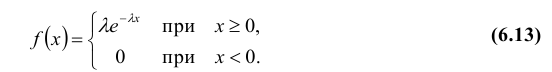
Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены соответственно на рис. 7.3 и рис. 7.4. 
Теорема. Функция распределения случайной величины Х, распределенной по показательному (экспоненциальному) закону, есть 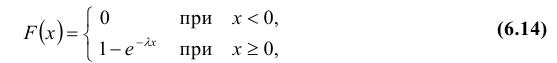 ее математическое ожидание
ее математическое ожидание  а дисперсия
а дисперсия

Отсюда следует, что для случайной величины, распределенной по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т.е. 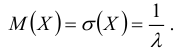
Вероятность попадания в интервал [a; b] непрерывной случайной величины Х, распределенной по показательному закону, находится как 
Пример:
Установлено, что время ремонта железнодорожных вагонов есть случайная величина Х, распределенная по показательному закону. Определить вероятность того, что на ремонт вагона потребуется менее 7 дней, если среднее время ремонта вагонов составляет 10 дней.
Решение:
По условию математическое ожидание М(Х) = 1/λ = 10, откуда параметр λ = 0,1. По формуле (6.17) находим вероятность попадания случайной величины Х в интервал [0, 7]: 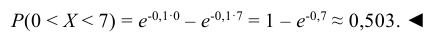
Показательный закон распределения играет большую роль в теории массового обслуживания. Так например, интервал времени между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром λ – интенсивностью потока. Кроме того, показательное распределение широко применяется в теории надежности, одним из основных понятий которой является функция надежности.
Функция надежности
Будем называть элементом некоторое устройство. Пусть элемент начинает работать в момент времени 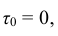 , а по истечении времени τ происходит отказ. Обозначим через Т непрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно (т.е. до наступления отказа) время, меньшее чем τ, то, следовательно, за время длительностью τ наступил отказ.
, а по истечении времени τ происходит отказ. Обозначим через Т непрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно (т.е. до наступления отказа) время, меньшее чем τ, то, следовательно, за время длительностью τ наступил отказ.
Таким образом, интегральная функция 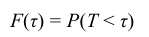 определяет вероятность отказа за время длительностью τ. Следовательно, вероятность безотказной работы за это же время, длительностью τ, т.е. вероятность противоположного события Т > τ, равна
определяет вероятность отказа за время длительностью τ. Следовательно, вероятность безотказной работы за это же время, длительностью τ, т.е. вероятность противоположного события Т > τ, равна 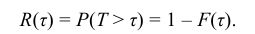
Функцией надежности R(τ), называют функцию, определяющую вероятность безотказной работы элемента за время длительностью τ:  где λ – интенсивность отказов.
где λ – интенсивность отказов.
Широкое использование показательного закона распределения обусловлено тем, что только он обладает следующим важным свойством: Если промежуток времени Т, распределенный по показательному закону, уже длился некоторое время τ, то это никак не влияет на закон распределения оставшейся части 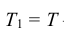 – τ промежутка, т.е. закон распределения
– τ промежутка, т.е. закон распределения 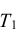 остается таким же, как и всего промежутка Т.
остается таким же, как и всего промежутка Т.
Пример:
Время безотказной работы устройства распределено по показательному закону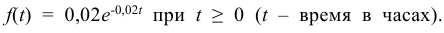 Какова вероятность того, что устройство проработает безотказно 50 часов?
Какова вероятность того, что устройство проработает безотказно 50 часов?
Решение:
По условию постоянная интенсивность отказов λ = 0,02. Используя формулу (6.18), получаем: 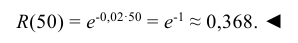
Нормальный закон распределения
Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Определение: Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и 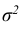 , если ее плотность вероятности f(x) имеет вид:
, если ее плотность вероятности f(x) имеет вид: 
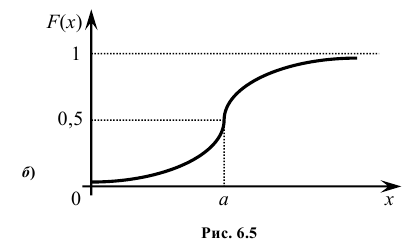
Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рис. 6.5 а), б) показана нормальная кривая с параметрами а и 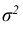 и график функции распределения.
и график функции распределения.
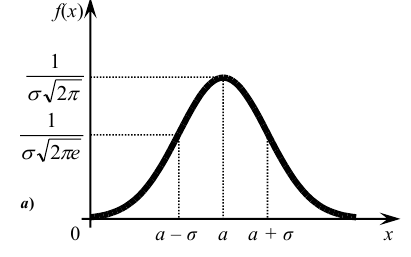
Обратим внимание на то, что нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный 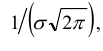 и две точки перегиба х =
и две точки перегиба х =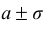 с ординатами
с ординатами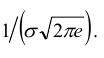
Можно заметить, что в выражении плотности нормального закона параметры распределения обозначены буквами а и 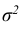 , которыми мы обозначали математическое ожидание и дисперсию. Такое совпадение не случайно. Рассмотрим теорему, которая устанавливает теоретико-вероятностный смысл параметров нормального закона.
, которыми мы обозначали математическое ожидание и дисперсию. Такое совпадение не случайно. Рассмотрим теорему, которая устанавливает теоретико-вероятностный смысл параметров нормального закона.
Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру a этого распределения, т.е.  а ее дисперсия – параметру
а ее дисперсия – параметру 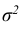 , т.е.
, т.е.

Выясним, как будет меняться нормальная кривая при изменении параметров а и σ. Если σ = const, и меняется параметр a (а1 < а2 < а3), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 6.6).
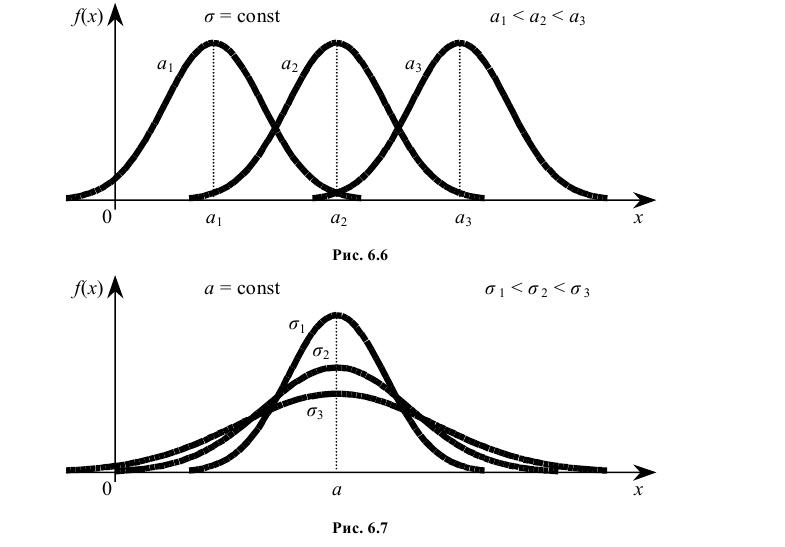
Если а = const и меняется параметр σ, то меняется ордината максимума кривой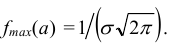 При увеличении σ ордината максимума уменьшается, но так как площадь под любой кривой распределения должна оставаться равной единице, то кривая становится более плоской, растягиваясь вдоль оси абсцисс. При уменьшении σ, напротив, нормальная кривая вытягивается вверх, одновременно сжимаясь с боков (рис. 6.7).
При увеличении σ ордината максимума уменьшается, но так как площадь под любой кривой распределения должна оставаться равной единице, то кривая становится более плоской, растягиваясь вдоль оси абсцисс. При уменьшении σ, напротив, нормальная кривая вытягивается вверх, одновременно сжимаясь с боков (рис. 6.7).
Таким образом, параметр a характеризует положение , а параметр σ – форму нормальной кривой.
Нормальный закон распределения случайной величины с параметрами a = 0 и σ = 1 называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной. Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, связана с тем, что интеграл от функции нормального распределения не выражается через элементарные функции. Однако его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения 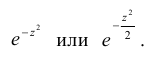
Такую функцию называют функцией Лапласа, для нее составлены таблицы. Существует много разновидностей такой функции, например:
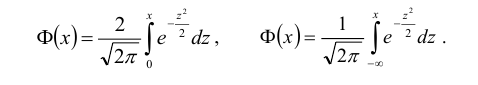
Мы будем использовать функцию:

Для такой функции табличные значения приведены в Приложении 2.
Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле

Рассмотрим свойства случайной величины, распределенной по нормальному закону.
1. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал [α, β] равна
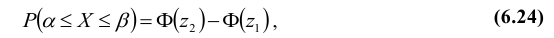
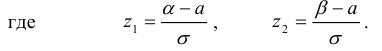
2. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания a не превысит величину δ > 0 (по абсолютной величине), равна
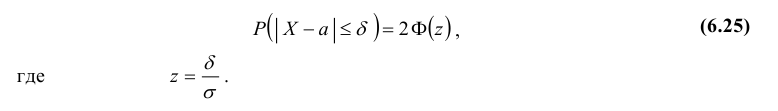
Вычислим по этой формуле вероятности 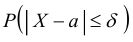 при различных значениях δ (используя таблицу значений функции Лапласа):
при различных значениях δ (используя таблицу значений функции Лапласа): 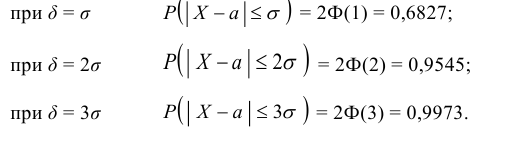 Отсюда вытекает так называемое «правило трех сигм»: Если случайная величина Х имеет нормальный закон распределения с параметрами a и σ, то практически достоверно, что ее значения заключены в интервале (a – 3σ; a + 3σ).
Отсюда вытекает так называемое «правило трех сигм»: Если случайная величина Х имеет нормальный закон распределения с параметрами a и σ, то практически достоверно, что ее значения заключены в интервале (a – 3σ; a + 3σ).
Пример:
Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина Х с параметрами а = 173 и 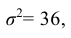 найти: 1. Выражение плотности вероятности и функции распределения случайной величины Х; 2. Долю костюмов 4-го роста (176 – 183 см) и долю костюмов 3-го роста (170 – 176 см), которые нужно предусмотреть в общем объеме производства для данной возрастной группы; 3. Сформулировать «правило трех сигм» для случайной величины Х.
найти: 1. Выражение плотности вероятности и функции распределения случайной величины Х; 2. Долю костюмов 4-го роста (176 – 183 см) и долю костюмов 3-го роста (170 – 176 см), которые нужно предусмотреть в общем объеме производства для данной возрастной группы; 3. Сформулировать «правило трех сигм» для случайной величины Х.
Решение:
1. Находим плотность вероятности 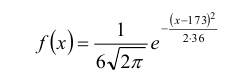 и функцию распределения случайной величины Х
и функцию распределения случайной величины Х 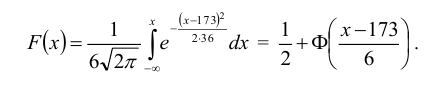 2. Долю костюмов 4-го роста (176 – 182 см) находим как вероятность
2. Долю костюмов 4-го роста (176 – 182 см) находим как вероятность 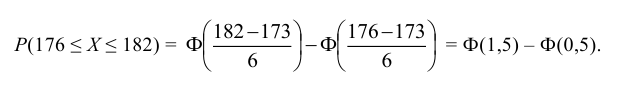
По таблице значений функции Лапласа (Приложение 2) находим: 
Окончательно получаем 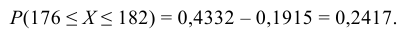
Долю костюмов 3-го роста (170 – 176 см) можно найти аналогично. Однако проще это сделать, если учесть, что данный интервал симметричен относительно математического ожидания а = 173, т.е. неравенство 170 ≤ Х ≤ 176 равносильно неравенству │Х – 173│≤ 3. Тогда 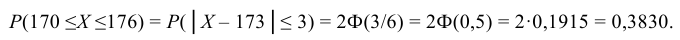
3. Сформулируем «правило трех сигм» для случайной величины Х: Практически достоверно, что рост мужчин данной возрастной группы заключен в границах от 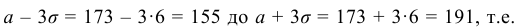
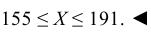
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |