Основные законы распределения дискретных случайных величин с примерами решения

Содержание:

Нами были рассмотрены случайные явления, наблюдаемые результаты которых после проведения опыта представлялись в виде случайных событий. Например, результат выстрела сводился к попаданию в цель или промаху. Можно сказать, что событие характеризует как бы качественный результат опыта, который при оценке эффективности стрельбы на поражение не всегда нас удовлетворяет. Действительно, поражение цели может быть достигнуто не только при прямом попадании в цель, но и при промахе при условии, что отклонение разрыва от цели не превышает какой-то определенной величины. Чтобы правильно оценить эффективность стрельбы в таких условиях, нужно знать, на каком именно удалении разрывов от цели цель будет поражаться, т.е. данное случайное явление необходимо оценивать не с качественной, а с количественной стороны. Именно подобные обстоятельства и привели к необходимости ввести в рассмотрение теорией вероятностей случайные величины.

Понятие о случайной величине и законе ее распределения

Случайной величиной называется такая переменная величина, которая при испытании может принимать то или иное частное значение, причем заранее неизвестно какое.

Можно дать и несколько иное определение случайной величины:

Величина, значения которой от испытания к испытанию изменяются случайным образом, называется случайной величиной.

Случайные величины принято обозначать прописными буквами X; У; Z ... , а возможные частные значения, которые может принять случайная величина, - соответственно строчными буквами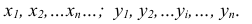

Если не указывается, какое именно из возможных значений принимает случайная величина, её могут обозначать как х; у.

Понятие случайной величины является фундаментальным понятием теории вероятностей и играет большую роль в её приложениях. Введение понятия случайной величины значительно расширило возможности теории вероятностей при исследовании случайных явлений. Заслуга широкого внедрения в теорию вероятностей понятия «случайная величина» принадлежит русскому учёному П.Л. Чебышеву.

Приведём ряд примеров случайных величин.

Пример:

По цели производится 3 выстрела. Число попаданий в цель при трёх выстрелах является случайным.

Случайная величина X = {число попаданий в цель при трёх выстрелах}.

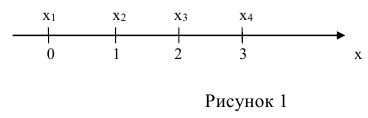
Случайная величина X = {число попаданий в цель при трёх выстрелах} в результате опыта может принять следующие частные значения: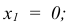

Эти частные значения случайной величины (рисунок 1) могут быть расположены на числовой оси изолированно, причём в определенной последовательности (пронумерованы), и могут быть определены до опыта.

Пример:

Стрельба по цели ведётся до первого попадания. Число снарядов, необходимых для получения попадания в цель является случайным.

Случайная величина Y = {число снарядов, необходимых для получения одного попадания}.

Случайная величина Y = {число снарядов, необходимых для получения одного попадания} в результате опыта может принять следующие частные значения:

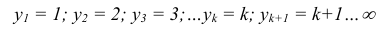
Возможные частные значения случайной величины Y = {число снарядов, необходимых для получения одного попадания} (рисунок 2) также как и в первом примере могут быть расположены на числовой оси в определенной последовательности изолированно, и могут быть определены до опыта.

Однако в отличие от случайной величины X, возможных значений случайной величины Y бесконечно много (но при этом счётно, так как их можно пересчитать).

Пример:

Производится несколько выстрелов из орудия. Отклонение точек падения снарядов от центра рассеивания снарядов случайно.

Случайная величина Х={удаление точки падения снаряда от центра рассеивания снарядов}.

Рассеивание снарядов неравномерно, симметрично и небеспредельно.

Таким образом, снаряд может упасть в любую точку интервала, ограниченного пределами технического рассеивания снарядов от 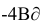до.

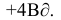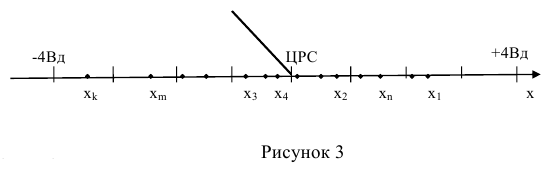
Следовательно, все числа из этого интервала будут возможными значениями случайной величины X = {удаления точки падения снарядов от центра рассеивания снарядов (ЦРС)}.

Характерной особенностью данной случайной величины X (рисунок 3) является то, что перечислить все ее частные значения (или все точки интервала числовой оси) не представляется возможным, т.к. их число бесконечно и несчетно. Для подобной случайной величины X можно указать лишь границы, в которых она может появиться.

Из приведенных выше примеров мы видим, что случайные величины могут принимать как отдельные (счётные), имеющие конечное или бесконечное множество значений, так и непрерывно заполнять некоторый промежуток числовой оси (иметь несчётное множество возможных значений).

Исходя из этого, различают следующие типы случайных величин: дискретные (прерывные) и непрерывные.

Дискретная (прерывная) случайная величина - это такая случайная величина, которая в результате испытаний может принимать только отдельные изолированные значения.

Характерными особенностями дискретной случайной величины являются:

1. возможные значения дискретной случайной величины на числовой оси располагаются изолированно;
2. число возможных значений дискретной случайной величины может быть как конечно так и бесконечно, но оно всегда счётно;
3. возможные значения дискретной случайной величины могут быть перечислены заранее до опыта.

Непрерывная случайная величина - это такая случайная величина, которая в результате испытания может принимать любое значения из бесчисленного множества значений некоторого промежутка.

Характерными особенностями непрерывной случайной величины являются:

1. возможные значения непрерывной случайной величины непрерывно заполняют некоторый промежуток числовой оси;
2. возможные значения непрерывной случайной величины нельзя расположить в определенной последовательности (пересчитать), их бесчисленное множество;
3. возможные значения непрерывной случайной величины нельзя перечислить до опыта, возможно указать лишь границы промежутка, в которых она может появиться.

В результате опыта случайная величина может принимать то или иное частное значение. Очевидно, что знание возможных значений случайной величины 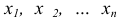ещё не позволяет полностью описать случайную величину X. Необходимо ответить на вопрос - как часто в результате повторения опыта в одних и тех же условиях следует ожидать появления тех или иных возможных значений случайной величины. Другими словами, какова вероятность появления различных частных значений случайной величины. Причём, для дискретных случайных величин имеется возможность установить ряд этих значений, а для непрерывных -промежутки этих значений.

Вернёмся к примеру 1. Так как несовместные события 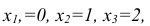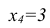образуют полную группу, то должно выполняться условие:

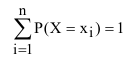
Очевидно, что эта суммарная вероятность каким-то образом распределена между отдельными значениями случайной величины X = Xj.

С вероятностной точки зрения дискретная случайная величина X будет полностью описана в том случае, если мы в точности укажем, какой вероятностью обладает каждое из событи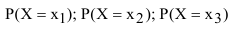й: и 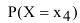, а для случайной непрерывной величины вероятность того, что случайная величина примет значение некоторого промежутка числовой оси -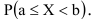

Таким образом, вводится новое, очень важное понятие теории вероятностей - закон распределения случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными частными значениями случайной величины и соответствующими им вероятностями.

Про случайную величину в этом случае говорят, что она подчинена данному закону распределения.

Закон распределения является исчерпывающей вероятностной характеристикой случайной величины, полностью описывающий с вероятностной точки зрения поведение случайной величины.

Формы закона распределения случайной величины: ряд распределения, функция распределения, функция плотности распределения

Способы или формы представления закона распределения случайной величины могут быть различны.

Наиболее просто решается задача вероятностной оценки для дискретной случайной величины. Для этого достаточно указать, какой вероятностью обладает каждое из событий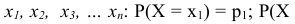

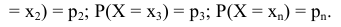
Рассмотрим дискретную случайную величину X = {число попаданий при 3 выстрелах}.

Пусть вероятность попадания в цель равна 0,3 и от выстрела к выстрелу не изменяется.

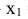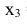Возможные частные значения случайной величины X = {число попаданий при 3 выстрелах} могут быть следующими: ни одного попадания - = 0; одно попадание - = 1; два попадания - = 2; все три попадания - 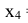= 3.

Вероятности частных значений случайной величины найдём по формуле Бернулли:

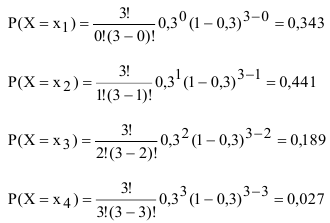
Проведём проверку учета всех гипотез:

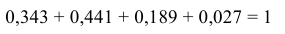
Таким образом, мы определили вероятность наступления каждого из всех несовместных событий и с вероятностной точки зрения полностью охарактеризовали случайную величину X = {число попаданий при 3 выстрелах}, поставив в соответствие каждому частному значению случайной величины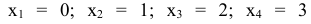 вероятность его появления: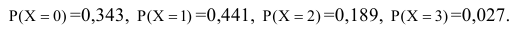

Такая форма закона распределения дискретной случайной величины называется рядом распределения.

Закон распределения дискретной случайной величины, когда каждому частному значению 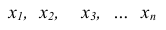случайной величины X ставится в соответствие её вероятность:

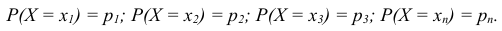
называется рядом распределения дискретной случайной величины.

Ряд распределения, как правило, представляют в виде таблицы, где в верхней строке в порядке возрастания размещают возможные частные значения случайных величин, а в нижней - соответствующие им вероятности.

При составлении ряда распределения следует иметь в виду, что все события являются несовместными, т.к. случайная величина X может принять в результате испытания только одно значение. Эти события случайны, т.к. нельзя указать, какое значение примет случайная величина и, последнее, все события должны образовывать полную группу событий, т.к. никаких других событий, кроме перечисленных, в результате опыта произойти не может.

На основании вышеизложенного, что события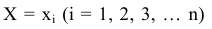 образуют полную группу несовместных событий, сумма вероятностей всех возможных частных значений должна удовлетворять условию:

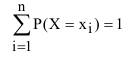
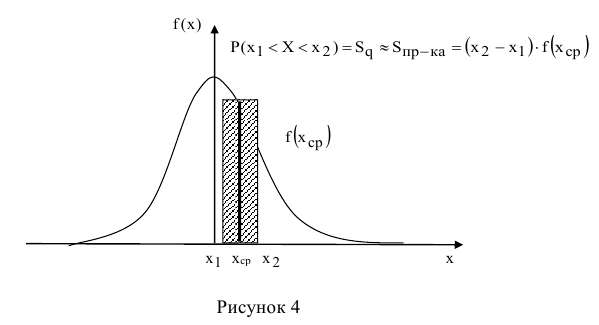
Ряд распределения можно представить графически, для этого по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат - вероятности этих значений (рисунок 4).

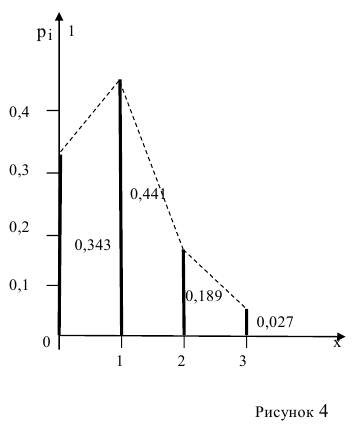
Для наглядности вершины полученных ординат соединяют пунктирными отрезками. Следует помнить, что соединение вершин прямыми делается только в целях наглядности, т.к. в промежутках между 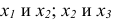и т.д., дискретная случайная величина X значений принять не может, следовательно, вероятность ее появления в этих промежутках равна 0. Полученную фигуру называют многоугольником распределения.

Рассмотренный ряд распределения является весьма удобной формой представления закона распределения. Однако основным недостатком данной формы закона распределения является то, что область его применения ограничивается распределением дискретной случайной величины с конечным числом возможных значений.

Для непрерывной случайной величины, когда возможные значения случайной величины заполняют всю числовую ось или какой-то ее интервал, поставить в соответствие каждому частному значению случайной величины соответствующую ему вероятность, невозможно. Множество возможных значений такой случайной величины несчетно (их невозможно перечислить в верхней части таблицы). Это вызывает необходимость иметь такую форму представления закона распределения, которая была бы приемлема не только для вероятностной характеристики дискретной случайной величины, но и для непрерывной, когда необходимо определить вероятность появления случайной величины на некотором промежутке числовой оси.

То есть, иметь какую то универсальную форму закона распределения для всех типов случайной величины.

Для количественной характеристики распределения как дискретной, так и непрерывной случайной величины, удобно воспользоваться не вероятностью события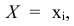, а вероятностью события X < х, где х -некоторая текущая переменная. Вероятность такого события есть некоторая функция от х - F(x). Эта функция носит название функции распределения случайной величины X.

Функцией распределения случайной величины X называется функция аргумента х, равная вероятности того, что случайная величина примет любое значение, меньше чем х.

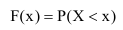
На примере дискретной случайной величины X = {число попаданий при 3 выстрелах} покажем, как возможно составить фикцию распределения. (Однако здесь необходимо несколько абстрагироваться от того, что число попаданий может быть только натуральными числами: 0, 1,2, 3, но и иметь дробное значение, а также меньше 0 и больше 3, т.е. рассмотреть все возможные значения числовой оси).

Рассчитаем функцию распределения дискретной случайной величины X = {число попаданий при 3 выстрелах}:

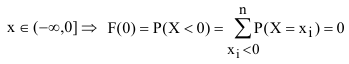событие невозможное

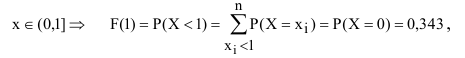
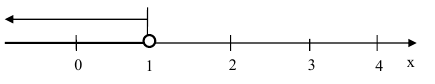
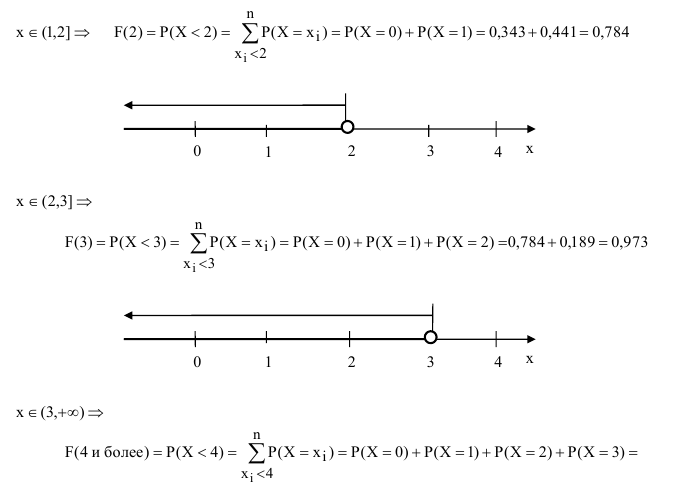
= 0,973 + 0,027 = 1

Таким образом, функция распределения случайной величины Х= {число попаданий при 3 выстрелах} будет иметь следующий вид:

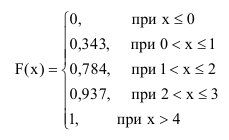
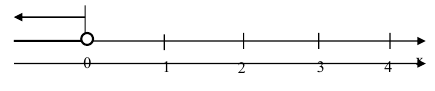
Отобразим полученную функцию распределения F(x) в виде графика (рисунок 5):

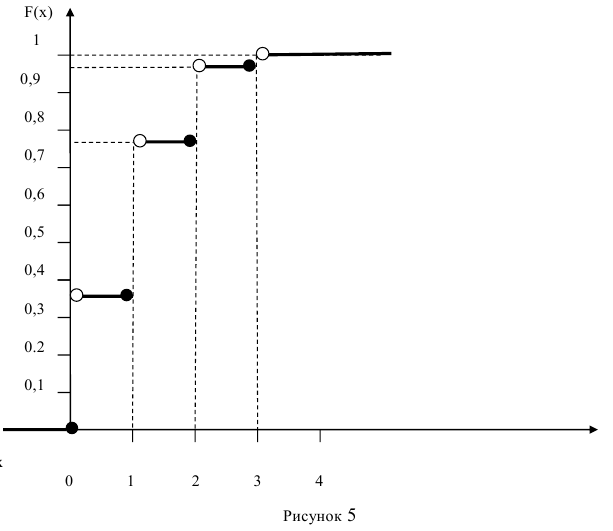
Функция распределения дискретной случайной величины является ступенчатой функцией.

Из графика функции распределения (рис. 5) видно, что в возможных частных значениях дискретной случайной величины X функция разрывается и поднимается скачками на величину вероятности соответствующего значения случайной величины.

Значение функции распределения в точке разрыва определяется при подходе к этой точке слева по оси Ох.

Сумма всех скачков функции F(x) равна 1 (в соответствии с условием:

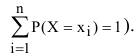
По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки - меньше, ступенчатая кривая становится более плавной, дискретная случайная величина постепенно приближается к непрерывной, а ее функция распределения - к непрерывной функции.

В принципе, любую непрерывную величину можно рассматривать как дискретную. Ведь измеряя какое-то ее значение по результатам опыта, например, удаление точки падения снаряда от цели, мы всегда выражаем ее в каких-то единицах измерения (метрах, сантиметрах). В реальности такая замена не всегда оправдана так как, во-первых, всегда имеется потенциальная возможность повысить точность измерения, а во-вторых, частные значения случайной величины могут быть очень тесно расположены на числовой оси. В этих случаях проще рассматривать случайную величину не как дискретную, а как сплошь занимаемую какой-то интервал числовой оси.

На рисунке 6 приведена функция распределения для непрерывной случайной величины, имеющей нормальное распределение.

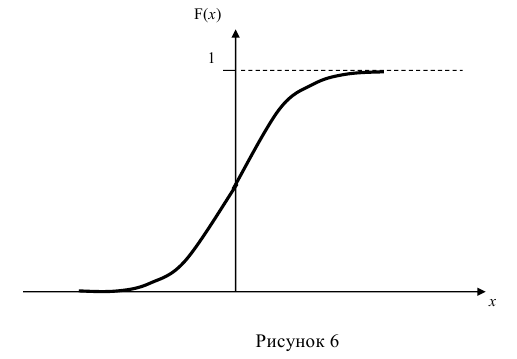
Вероятный смысл функции распределения состоит в том, что она определяет распределение вероятности между отдельными включающими друг друга участками интервала возможных значений случайной величины.

Сформулируем общие свойства функции распределения:

1.    Функция распределения F(x) есть неотрицательная функция, заключенная между 0 и 1

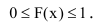
2.    Функция распределения F(x) есть неубывающая функция своего аргумента

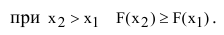
3.    На минус бесконечности функция распределения равна нулю

4.    На плюс бесконечности функция распределения равна 1

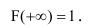
Кроме того, из графика функции распределения F(x) (рисунок 6) видно, что значение функции распределения в точке разрыва определяется при подходе к этой точке слева по оси Ох. Это означает, что функция распределения непрерывна слева.

Таким образом, функция распределения F(x) любой случайной величины есть неотрицательная, неубывающая, непрерывная слева функция своего аргумента, значения которой заключены между нулем и единицей, причём 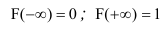.В отдельных точках эта функция может иметь скачки, на некоторых участках она может быть постоянной, на других -постоянно возрастать.

Следует также отметить, что имеет место и обратное утверждение: каждая функция, удовлетворяющая вышеперечисленным условиям, является функцией распределения некоторой случайной величины.

Функция распределения самая универсальная форма представления закона распределения случайной величины и может характеризовать как дискретные, так и непрерывные случайные величины.

Существенным недостатком такой формы закона распределения случайной величины, как функция распределения, является то, что она не позволяет ответить на вопрос в окрестностях какой из точек а или b будет чаще появляться непрерывная величина (рисунок 7).

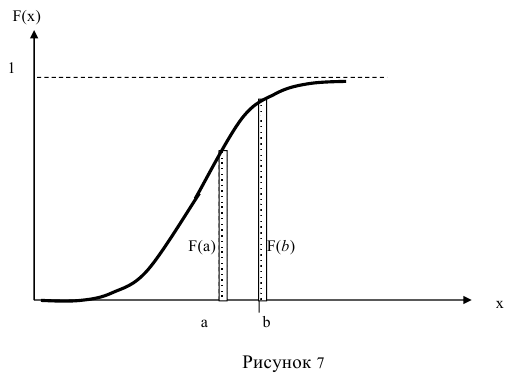
Для более наглядного характера распределения непрерывной случайной величины в окрестностях различных точек вводится особая функция, называемая плотностью вероятности или плотностью распределения.

Предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от х до х+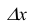 к длине этого участка 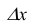, когда 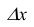стремится к нулю, называется плотностью распределения случайной величины в точке X.

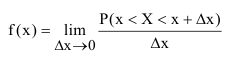
Функцию плотности распределения обозначают как f(x).

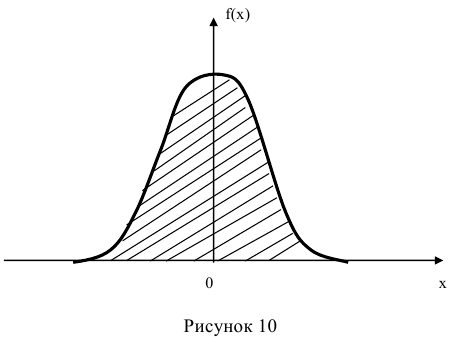
Кривая, изображающая плотность распределения случайной величины, называется кривой распределения

На рисунке 8 приведена кривая плотности распределения непрерывной случайной величины имеющей нормальное распределение.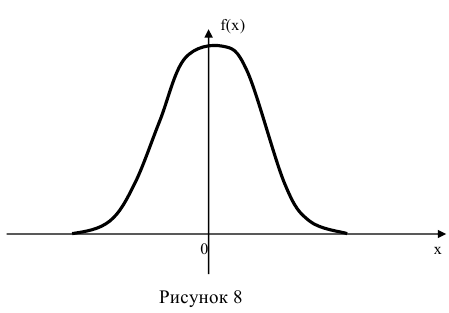

Физический смысл плотности распределения заключается в том, что
она указывает на то, как часто появляется случайная величина в малой окрестности точки х при повторении испытаний (рисунок 9).

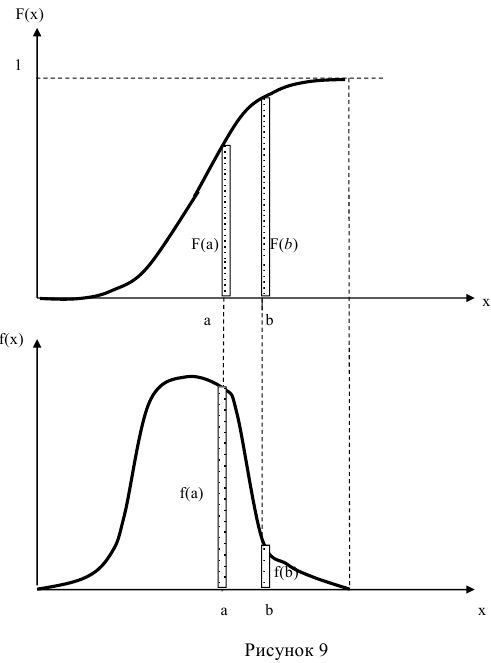
Если в точке X = а плотность распределения больше, чем в точке 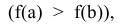то это означает, что в небольшой окрестности точки а при повторении испытаний случайная величина X будет появляться чаще, чем в такой же по величине окрестности вокруг точки X = b (при ).

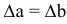Плотность распределения так же, как и функция распределения, есть одна из форм закона распределения. Однако, в противоположность функции распределения, являющейся универсальной формой закона распределения, плотность распределения существует только для непрерывных случайных величин.

Сформулируем основные свойства плотности распределения:

1.    Плотность распределения неотрицательна.

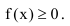
2.    Интеграл в бесконечных пределах от плотности распределения равен I.

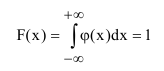
Геометрически это свойство плотности распределения означает, что вся площадь, ограниченная кривой распределения и осью абсцисс, равна 1 (рисунок 10).

Таким образом, подводя итог вышесказанному, закон распределения дискретной случайной величины может быть задан одним из следующих способов:

• •    формулой, с помощью которой можно вычислить вероятность всех возможных значений случайной величины;
• •    рядом распределения;
• •    функцией распределения.

Закон распределения непрерывной случайной величины может быть задан:

• •    формулой, с помощью которой можно вычислить вероятность попадания случайной величины в заданный интервал;
• •    функцией распределения;
• •    функцией плотности распределения.

Формула Бернулли

Перед изложением третьего вопроса лекции преподаватель обозначает проблему, вызывающую необходимость рассмотрения теоремы о повторении опытов, при этом отмечая, что в изучаемом курсе теории вероятностей будет рассматриваться только частная теорема, связанная с повторением независимых опытов, в каждом из которых событие А появляется с постоянной вероятностью.

После чего преподаватель показывает доказательство этой теоремы (вывод формулы Бернулли).

Для пояснения физической сущности рассматриваемой теоремы преподаватель использует оверхэд-проектор и подготовленные слайды.

В заключении лекции преподаватель поясняет почему распределение вероятностей появления события А в серии из п испытаний, в условиях когда они несовместны и образуют полную группу событий называют биномиальным и обращает внимание на важность знания этого распределения для решения прикладных задач.

До сих пор мы рассматривали комбинации сравнительного небольшого числа событий, когда непосредственное применение правил сложения и умножения вероятностей не вызывало больших вычислительных затруднений. Однако с увеличением числа событий или числа испытаний, в которых может появляться интересующее нас событие, изученный способ вычисления становится очень громоздким.

При этом задача решалась достаточно просто только в том случае, если опыты являлись независимыми.

Несколько опытов называются независимыми, если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты.

На практике имеют место случаи, когда вероятность наступления события А во всех независимых опытах может быть либо одинаковой, либо меняться от опыта к опыту. Например, при корректировании огня после каждого выстрела вероятность попадания в цель с каждым выстрелом будет изменяться.

В случае, когда в независимых опытах вероятность наступления события от опыта к опыту изменяется, используют общую теорему о повторении опытов, а когда в независимых опытах вероятность наступления события от опыта к опыту не изменяется, используют частную теорему о повторении опытов.

В изучаемом нами курсе теории вероятностей мы рассмотрим только частную терему о повторении опытов, когда необходимо определить вероятность наступления события А в серии из п независимых опытов, в каждом из которых событие А появляется с одинаковой вероятностью.

Например, необходимо вычислить вероятность того, что при пяти выстрелах из орудия на постоянных установках будет получено ровно два попадания в цель, если выстрелы независимы и при каждом выстреле вероятность попадания в цель известна и не изменяется.

В случае, если составить возможные комбинации появления интересующего нас события , то получим:

т.д.

Возможных комбинаций, в которых наступит событие А= {получить 2 попадания при пяти выстрелах} будет 10.

Применив теорему о сумме и произведении независимых событий, будем иметь:

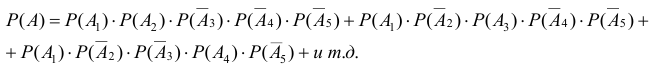
Увеличение числа интересующих нас событий или числа испытаний приведёт к еще большему увеличению объёма вычислительных операций, поэтому возникает задача отыскания менее трудоёмких способов расчёта. Пост а новка за да ч и:

Пусть предполагается в одинаковых условиях произвести п независимых испытаний, результатом каждого из которых может быть наступление либо события А, либо ему противоположного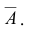

Обозначим через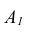 наступление события А при первом испытании, 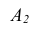- при втором испытании, 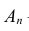- при последнем испытании.

В силу постоянства условий испытания:

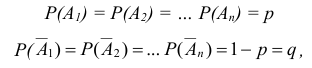
где: р = Р(А) - вероятность наступления события А в одном испытании;

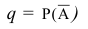- вероятность наступления противоположного события в одном испытании.

Нас интересует вероятность того, что событие А при п испытаниях наступит ровно m раз, а в оставшихся n-m испытаниях - не наступит (т.е. наступит противоположное событию А событие -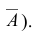

Допустим, что интересующее нас событие А наступает подряд m раз, начиная с первого, т.е. имеет место событие - Е.

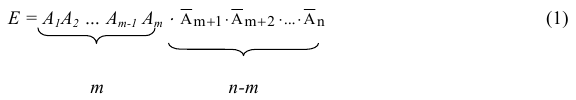
По условию повторения испытаний, события, входящие в данную комбинацию, независимы, при этом вероятности наступления событий 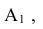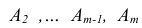одинаковы и равны р:  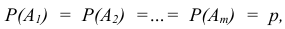а вероятности не наступления событий 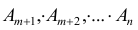так же одинаковы и равны q=l-p: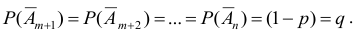

Применяя правило умножения вероятностей для независимых событий к выражению 1 получим:

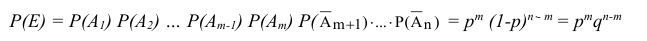
В силу постоянства условий испытаний мы допустили, что интересующее нас событие А наступает подряд ш раз, начиная с первого. Но событие А в /7 испытаниях может наступить ровно т раз в различных последовательностях или комбинациях. При этом нам безразлично, в какой именно последовательности появляется событие А ровно т раз.

Число таких комбинаций равно числу сочетаний 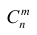из п элементов по
т.

Так как эти комбинации событий (подобные комбинации Е) несовместны и нас не интересует последовательность наступления события А в испытании ровно m раз, то обозначив интересующую нас вероятность через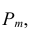получим: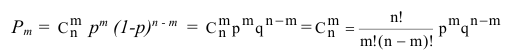

где 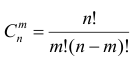число сочетании из n элементов по m.

Данная формула носит имя формулы Бернулли.

Формула Бернулли позволяет получить ответ на вопрос: какова

вероятность того, что при повторении п независимых испытаний некоторое событие А наступает ровно m раз, если в каждом из этих испытаний вероятность наступления события А постоянна и равна Р(А) = р.

Приведенная формула Бернулли имеет исключительно важное значение в теории вероятностей по той причине, что она связана с повторением испытаний в одинаковых условиях, т.е. с такими условиями, в которых как раз и проявляются законы теории вероятностей.

Заключение по лекции:

В лекции мы рассмотрели принципиальные вопросы теории вероятностей применительно к случайным величинам, ввели основной понятийный аппарат, необходимый для дальнейшего изучения дисциплины: определение случайной величины, их классификацию; понятия закона распределения и его формы для различных типов случайной величины.

Основные законы распределения дискретных случайных величин. Локальная теорема Муавра-Лапласа, формула Пуассона

Сегодня мы рассмотрим основные распределения дискретных и непрерывных случайных величин.

Локальная теорема Муавра-Лапласа

При больших значениях п формула Бернулли приводит к громоздким вычислениям, поэтому вероятность 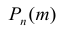находят по следующей приближённой формуле:

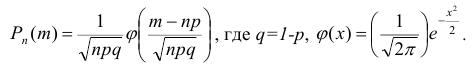
Эта формула называется формулой Муавра - Лапласа. В силу сложности вывод её опущен.

Распределение Пуассона

Достаточно часто в практике приходится иметь дело с редко наступающими однородными событиями, например, поступление информации в АСУ, сигналов о разведанных целях в РЛС и ряда подобных задач, связанных с моментом появления каких-то однородных событий. Такого рода случайные величины распределены по своеобразному закону, который называется законом Пуассона.

Дискретная случайная величина X имеет распределение Пуассона, если ее возможные значения: 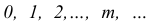(бесконечное, но счётное множество значений), а соответствующие вероятности находятся из выражения:

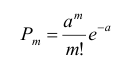
где а > 0,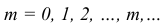

а - параметр закона Пуассона, от которого зависит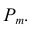
Ряд распределения случайной величины X, распределенной по закону Пуассона, имеет вид:
 

Опять же для решения задачи отыскания числовых характеристик дискретной случайной величины имеющей распределение Пуассона применяют аппарат производящих функций.

Математическое ожидание случайной величины X, имеющей распределение Пуассона с параметром а равно этому параметру.

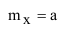
Дисперсия случайной величины X, имеющей распределение Пуассона с параметром а равна этому параметру.

Среднеквадратическое отклонение случайной величины X, распределенной по закону Пуассона, будет равно:

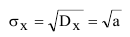
Если провести аналогии по вычислению вероятности появления события «не менее m числа раз» с биномиальным распределением, то мы увидим, что решить задачу отыскания искомой вероятности из выражения:

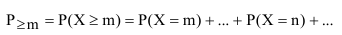 невозможно, так как число возможных значений случайной величины X бесконечно.

Следовательно, вероятность 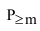может быть вычислена только как противоположное событие:

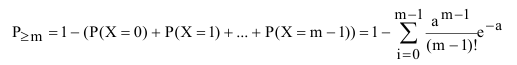
В частности вероятность появления события хотя бы один раз возможно вычислить из выражения:

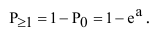
Закон Пуассона применяется для решения следующих типов прикладных задач:

1. Когда производится большое число независимых опытов, в каждом из которых событие А имеет очень малую вероятность наступления,
2. Когда на отрезке времени случайным образом появляются какие-то однородные события.

В первом случае, когда производится большое число независимых опытов, в каждом из которых событие А имеет очень малую вероятность наступления, возможна приближенная замена биномиального распределения распределением Пуассона.

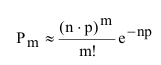
При этом параметр а Пуассоновского распределения равен произведению параметров биномиального распределения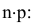

Пример №1

При стрельбе по цели расходуется 216 снарядов.

Вероятность попадания в цель одним снарядом равна 0,02. Определить вероятность того, что в цель попадет не более двух снарядов.

Решение:

Случайная величина X = {Число снарядов, попавших в цель} имеет биномиальное распределение, но так как производится достаточно большое число независимых выстрелов п = 216, а вероятность наступления события попадание в цель в каждом испытании мала р = 0,02, то для вычисления вероятности наступления интересующих событий можно воспользоваться законом Пуассона.

Таким образом:

 

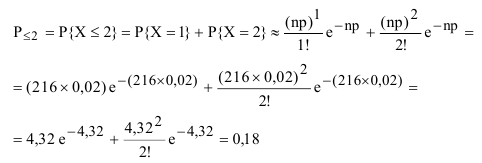
Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб по 216 снарядов в каждой в аналогичных условиях, в среднем, в 18 стрельбах из 100 в цель попадёт не более двух снарядов.

Из-за    возможной    замены    биномиального распределения распределением Пуассона, когда производится большее число испытаний, а вероятность наступления события в каждом из них мала, закон Пуассона называют также «законом «редких явлений».

Во втором случае закон Пуассона может применяться для решения задачи определения вероятности случайных появления однородных событий за промежуток времени.

Последовательность появления однородных событий называют «потоком событий». Для простейшего или стационарного Пуассоновского потока событий вероятность появления события за промежуток времени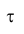 равна

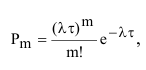
где 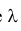- интенсивность потока событий.

Другими словами, 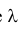- это средняя плотность появления однородных событий за время t, или математическое ожидание числа появления однородных событий за единицу времени.

В этом случае параметр а биномиального распределения равен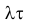

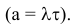
Пример №2

ЭВМ в среднем за 1 час может обработать сведения о 20 разведанных целях. Найти вероятность того, что в течение 12 минут будет обработана информация не более чем об одной цели.

Решение:

Случайная величина Х= {Число обработанных в ЭВМ целей за промежуток 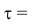12 минут} распределена по закону Пуассона, так как: среднее число обработанных целей за 12 минут пропорционально только возможности ЭВМ обработать сведения о поступивших целях за этот промежуток времени (поток обладает свойством стационарности); в случае, если ЭВМ обрабатывает результаты засечки одной цели, то за этот промежуток времени обработка результатов засечки другой цели невозможна (поток обладает свойством ординарности); информация о разведанных целях поступает от различных средств разведки, поэтому можно считать, что поступление информации в ЭВМ независимо (поток обладает свойством «отсутствие последействия»). Следовательно, поток событий можно считать стационарным Пуассоновским, а искомую вероятность определить из выражения.

Таким образом, искомая вероятность определится как:

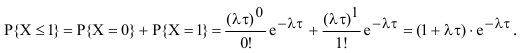
По условиям задачи интенсивность потока 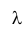= 20 целей/час; промежуток времени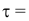12 минут = 1/5 часа.

Подставив исходные данные, получим:

 

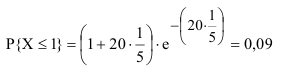
Вывод:    Полученный результат означает, что при проведении достаточно большого числа испытаний в аналогичных условиях, в среднем в 9 случаях из 100 за 12 минут будет обработана информация не более чем по одной цели.

Заключение по лекции:

В лекции мы рассмотрели основные распределения дискретных и непрерывных случайных величин, показали аналитические зависимости, позволяющие вычислить вероятность числа попаданий (для дискретных случайных величин) или вероятность попадания случайной величины на интервал (для непрерывных случайных величин), математического ожидания и дисперсии случайных величин.

Основные законы распределения дискретных случайных величин. Интегральная теорема Лапласа

Определение вероятности попадания случайной величины на интервал с использованием приведенной табличной функции распределения, приведенной табличной функции плотности распределения, приведенной табличной функции Лапласа:

Перед изложением материала лекции преподаватель обозначает проблему (невозможность определения вероятности попадания случайной величины имеющей нормальное распределение на интервал известными ранее методами) и пути её решения.

После чего преподаватель доводит условие примера, на котором будут показаны методы решения задачи по определению искомой вероятности.

Далее преподаватель последовательно решает задачу различными методами. При этом очень кратко останавливаясь на его содержании, доводит расчётную формулу и методику её решения.

Для более глубокого понимания сущности решаемой задачи и исходных данных, для каждого метода решения преподаватель изменяет начало отсчёта.

В общем виде вероятность попадания случайной величины на интервал определится как:

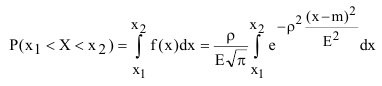
Однако данный интеграл не выражается через элементарные функции и для решения задачи вычисления вероятности вводят специальные табличные функции.

При этом исходят из условия, что центрированная случайная величина
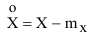должна быть выражена в числовых характеристиках рассеивания: либо 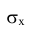либо Ех. В этом случае параметры нормально распределенной случайной величины будут равны 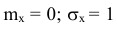или Ex = 1 (в зависимости от того, какую используют характеристику рассеивания 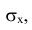или Ех). Для таких функций заранее составляют таблицы.

Методику решения задач по определению вероятности попадания нормально распределенной случайной величины на заданный интервал с использованием различных функций покажем на следующем примере.

Пример №3

Определить вероятность попадания при одном выстреле в полосу, глубиной 10 м, расположенную перпендикулярно направлению стрельбы, если центр рассеивания снарядов находится в 10 м дальше центра полосы. Срединное отклонение рассеивания снарядов по дальности равно 15 м (Вд=15) (рисунок 1)

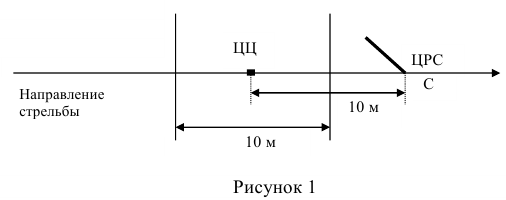
Решение:

Обозначим случайную величину X = {удаление точки падения снарядов от центра рассеивания снарядов (ЦРС)}.

Выберем за начало координат точку С, совпадающую с центром рассеивания снарядов, тогда математическое ожидание случайной величины равно 0 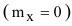, а удаление границ интервала, в котором необходимо определить вероятность попадания случайной величины X, будет равно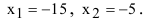

Таким образом, задача определения вероятности попадания снаряда в полосу глубиной, равную 10 м, сводится к определению вероятности попадания случайной величины X на интервал от -15 до -5, т.е.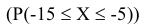 (рисунок 2).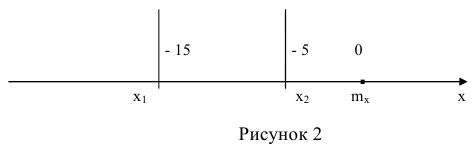
 

Определение вероятности попадания случайной величины X с использованием приведенной табличной функции распределения

Приведенная табличная функция распределения имеет вид:

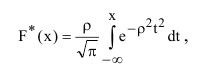
В основу определения вероятности попадания случайной величины X на интервал от 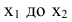с использованием табличной функции распределения положено, что (рисунок 3)

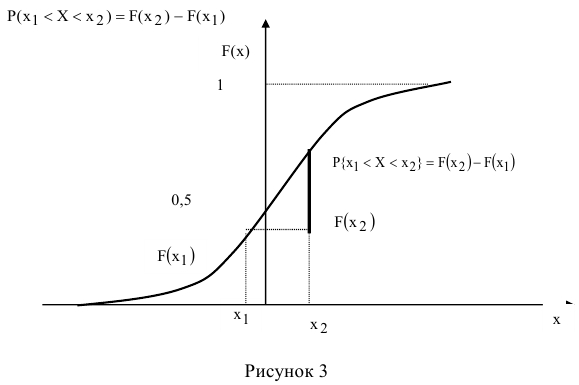
Выражение для определения вероятности с использованием приведенной табличной функции распределения имеет вид:

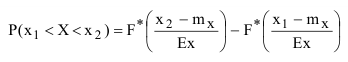
Подставив значения 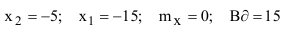в выражение для определения вероятности попадания на интервал(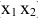) получим:

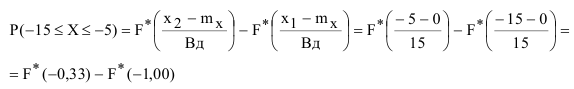
Значение функции распределения по известному аргументу определим из

Таблицы 1 Приложения к Практикуму:

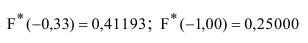
Таким образом, искомая вероятность будет равна:

 

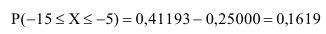
Определение вероятности попадания случайной величины на заданный интервал с использованием табличной функции плотности распределения

Приведенная табличная функция плотности распределения имеет вид:

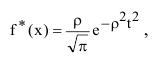
где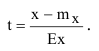

Решение данной задачи с использованием табличной функции плотности распределения предполагает вычисление площади
прямоугольника с высотой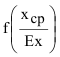и основанием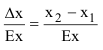(рисунок 4):

Выражения для определения вероятности с использованием приведенной табличной плотности распределения имеет вид:

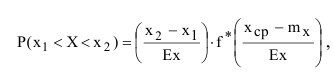
где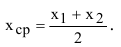

Несколько видоизменим условие задачи.

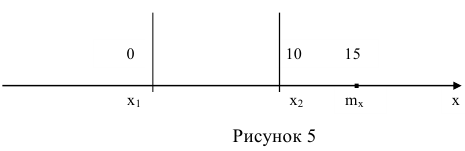
Выберем за начало координат ближнюю границу цели, тогда 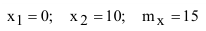(рисунок 5). Таким образом задача сведётся к определению вероятности попадания случайной величины X на интервал от 0 до 10 т.е. Р(0<Х< 10).

 

Решение:

Найдём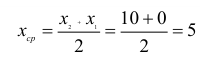и,подставив значения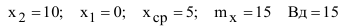в выражение для определения вероятности, получим:

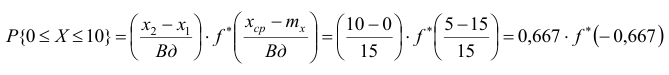
Зная, что функция плотности распределения четная 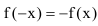, то:

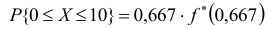
Значения функции плотности и распределения по известному аргументу определим по Таблице 2 Приложения к Практикуму:

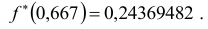
Таким образом, искомая вероятность будет равна:

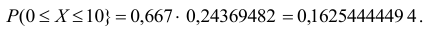
Следует отметить, что достаточную сходимость результатов решение задачи по вычислению вероятности с использованием табличной функции плотности распределения возможно получить при выполнении условия:

 

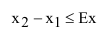
Определение вероятности попадания случайной величины на заданный интервал с использованием таблиц приведенной функции Лапласа

Приведенная функция Лапласа имеет вид:

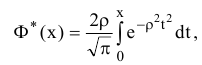
где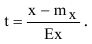
Вероятность попадания случайной величины на заданный интервал с использованием приведенной функции Лапласа определяется из выражения:

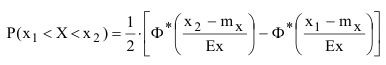
Решение.

Опять видоизменим условия задачи, выбрав за начало координат центр цели, тогда: 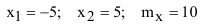  (рисунок 6).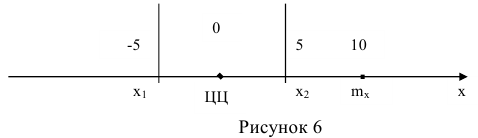

Таким образом задача сведётся к определению вероятности попадания случайной величины X на интервал от -5 до 5, т.е.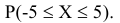

Подставив значения 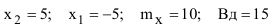в выражение для определения вероятности с помощью приведенной функции Лапласа, получим:

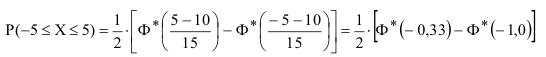
Так как функция Лапласа нечётная 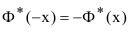, то

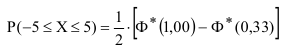
Значения приведенной функции Лапласа по известному аргументу определим из Таблицы 3 Приложения к Практикуму:

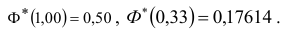
Таким образом, искомая вероятность будет равна:

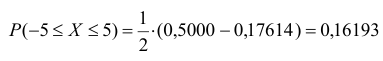
Рассчитанные значения вероятностей попадания случайной величины на заданный интервал различными способами дают достаточную близость полученных результатов.

Вывод:    Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 16 случаях из 100 будет получено попадание в полосу.

Сформулируем ряд основных свойств табличной функции Лапласа.

1.    Функция Лапласа является неотрицательной функцией:

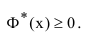
2.    Табличная функция Лапласа есть нечётная функция:

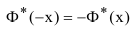
Определение дискретной случайной величины и её законы распределения

Раньше рассматривались случайные события, являющиеся качественной характеристикой случайного результата опыта. Для получения количественной характеристики вводится понятие случайной величины.

Понятие случайной величины

Определение 1. Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, причём заранее известно какое именно.

Примеры:

• 1)    Число очков, выпавших при однократном бросании игральной кости, есть случайная величина, она может принять одно из значений: 1,2,3,4, 5,6.
• 2)    Прирост веса домашнего животного за месяц есть случайная величина, которая может принять значение из некоторого промежутка.
• 3)    Число родившихся мальчиков среди пяти новорожденных есть случайная величина, которая может принять значение: 0, 1,2, 3, 4, 5.
• 4)    Расстояние между эпицентром взрыва бомбы и целью, на которую она сброшена, есть случайная величина, которая может принять любое неотрицательное значение.

Случайные величины будем обозначать прописными буквами X, Y, Z, а их возможные значения — соответствующими строчными буквами х, у, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: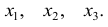

Случайные величины можно разделить на две категории: дискретные и непрерывные.

Определение 2. Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной.

Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать и бесконечное, хотя и счётное количество значений.

Случайные величины из примеров 1 и 3 дискретные.

Определение 3. Случайная величина, которая может принимать все значения из некоторого промежутка, называется непрерывной случайной величиной.

Случайные величины из примеров 2 и 4 являются непрерывными.

Очевидно, что число возможных значений непрерывной случайной величины бесконечно.

Для задания случайной величины недостаточно просто указать её значение, необходимо также указать вероятность этого значения.

Определение 4. Под суммой (произведением) случайных величин X и Y понимают случайную величину 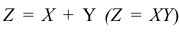, возможные значения которой состоят из сумм (произведений) каждого возможного значения величины X и каждого возможного значения величины Y.

Законы распределения дискретных случайных величин

Определение 5. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

Закон распределения может быть задан аналитически, в виде таблицы или графически.

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

В верхней строке выписываются все возможные значения 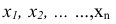 величины X, в нижней строке выписываются вероятности 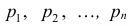значений 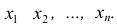. Читается таблица следующим образом: случайная величина X может принять значение 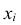с вероятностью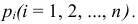

Так как в результате испытания величина х всегда примет одно из значений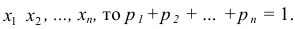

Графическое представление этой таблицы называется многоугольником распределения. При этом сумма всех ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.

Числовые характеристики: математическое ожидание, дисперсия, среднеквадратическое отклонение

Рассмотренный в лекции 8 закон распределения случайной величины позволяет с исчерпывающей полнотой описать случайную величину, т.е. указать, где располагаются возможные значения случайной величины и какова вероятность появления ее на том или ином интервале. Однако в ряде случаев достаточно иметь о случайной величине лишь некоторое общее представление, например, знать не весь закон распределения, а только некоторые характерные черты этого закона. В теории вероятностей для общей характеристики случайной величины используются некоторые величины, которые носят название числовых характеристик случайной величины. Оказывается, что при решении многих практических задач можно и не знать законы распределения случайной величины, достаточно знать лишь числовые характеристики этих величин, кроме того, определение числовых характеристик этих случайных величин осуществляется гораздо проще, нежели определение самого закона распределения.

Понятие о числовых характеристиках случайной величины

На прошлой лекции мы рассмотрели, что закон распределения дискретной случайной величины может быть задан одним из следующих способов: формулой, с помощью которой можно вычислить вероятность всех возможных значений случайной величины; рядом распределения; функцией распределения.

Закон распределения непрерывной случайной величины может быть задан: формулой, с помощью которой можно вычислить вероятность попадания случайной величины в заданный интервал; функцией распределения; функцией плотности распределения.

Однако для ряда непрерывных случайных величин определение закона распределения затруднительно. При этом о каждой случайной величине необходимо, прежде всего, знать ее некоторое среднее значение, вокруг которого группируются возможные частные значения случайной величины, наблюдаемые на опыте. Другими словами, необходимо знать, где находится так называемый «центр рассеивания» случайной величины.

Не менее важным при решении практических задач является знание того, насколько велик наблюдаемый на опыте разброс возможных частных значений случайной величины относительно ее среднего значения или центра рассеивания.

Числовые характеристики, с помощью которых оценивается положение центра рассеивания случайной величины, носят название числовых характеристик положения.

Числовые характеристики,    показывающие,    насколько тесно сгруппированы возможные частные значения случайной величины около центра рассеивания, носят название числовых характеристик рассеивания.

Кроме указанных числовых характеристик для более полного описания случайной величины могут использоваться и ряд других числовых характеристик, предназначенных для уяснения    характерных черт распределения случайной величины.

В теории вероятностей для характеристики случайной величины вводится понятие моментов. Однако, на настоящий момент изучения данной дисциплины мы ограничимся лишь понятием математического ожидания и дисперсии, а понятие «моментов» введём при изучении Темы 11 при рассмотрении системы нескольких случайных величин.

Числовые характеристики положения: математическое ожидание и его основные свойства

Математическое ожидание случайной величины является основной характеристикой, указывающей положение центра рассеивания случайной величины или иначе среднее ориентированное значение случайной величины, около которого группируются все возможные частные значения случайной величины.

Со средним значением случайной величины мы часто имеем дело в повседневной.

Рассмотрим дискретную случайную величину X, имеющую возможные значения 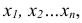с соответствующими вероятностями 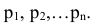Требуется каким-то числом охарактеризовать среднее значение случайной величины при условии того, что все эти значения имеют различные вероятности.

Для решения этой задачи воспользуемся так называемым «средним взвешенным» из значений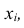 причём каждое значение 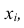будем учитывать с «весом», пропорциональным вероятности этого значения.

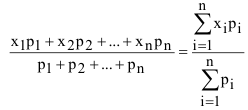
Учитывая, что мы имеем дело с полной группой несовместных событий
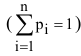получим:

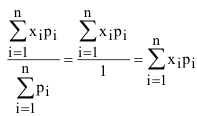
Таким образом, мы получили «среднее взвешенное» значение случайной величины X из значений 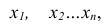с учётом «веса» пропорционального вероятности этих значений.

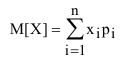
Это «среднее взвешенное» значение и является математическим ожиданием (средним значением) случайной величины X (обозначается М[Х] или ).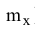

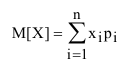
Математическим ожиданием дискретной случайной вели чины называется сумма произведений всех возможных значений случайной величины на вероятность этих значений.

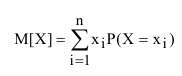
Для непрерывной случайной величины X математическое ожидание будет выражается уже не суммой, а интегралом вида:

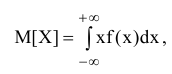
где: f(x) - плотность распределения случайной величины X.

f(x)dx - элемент вероятности - вероятность попадания непрерывной случайной величины Xна элементарный участок dx, прилежащий к точке X

Рассмотрим некоторые важные свойства математического ожидания случаиной величины.

1. Математическое ожидание постоянной величины с равно самой постоянной:

М[с] = с

2.    При прибавлении к случайной величине X постоянной величины с к её математическому ожиданию прибавляется та же величина:

М[Х + с] = М[Х] + с

3.    Постоянную величину с можно выносить за знак математического ожидания

М[сХ] = сМ[Х]

Математическое ожидание имеет размерность случайной величины и может быть целое, дробное, положительное и отрицательное.

Кроме математического ожидания в качестве характеристик положения используются также мода - M, и медиана - Me случайной величины.

Числовые характеристики рассеивания: дисперсия, среднеквадратическое отклонение

Для более полной характеристики случайной величины, кроме её какого то среднего положения, необходимо знать, насколько тесно

группируются её возможные значения около центра рассеивания. Наиболее широкое распространение для описания рассеивания случайных величин в артиллерийской практике нашли следующие числовые характеристики: дисперсия, среднеквадратическое отклонение и    срединное    отклонение случайной величины.

Так как мы говорим о характеристиках, показывающих, насколько тесно сгруппированы возможные значения    случайной    величины относительно центра рассеивания, то при определении указанных характеристик должна быть использована разность между случайной величиной и её математическим ожиданием: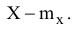

Эту разность, или отклонение случайной величины от её математического ожидания называют центрированным    значением случайной величины X (обозначается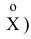

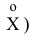= X -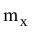

Определим математическое ожидание    (среднее    значение) центрированного значения случайной величины:

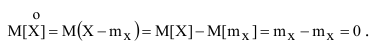
Таким образом, среднее значение отклонения случайной величины от её математического ожидания 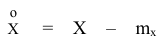не может служить характеристикой рассеивания случайной величины, так как это отклонение равно 0.

Рассмотрим возможность использования в качестве меры рассеивания случайной величины математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

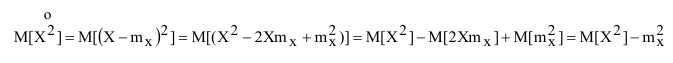
Таким образом, в качестве характеристики рассеивания случайной величины возможно использовать математическое ожидание квадрата отклонения случайной величины от её математического ожидания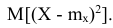

Квадрат этого отклонения называют дисперсией (в переводе «рассеивание») случайной величины X (обозначается D[X] или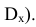

Дисперсией случайной величины называется математическое ожидание    квадрата    отклонения    случайной величины    от её математического ожидания.

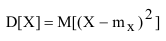
Для решения практических задач с целью сокращения вычислительных операций используется выражение, полученное в результате обоснования возможности применения математического ожидания квадрата отклонения случайной величины от её математического ожидания в качестве меры рассеивания:

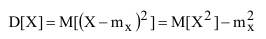
где: 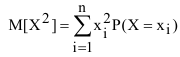   - математическое ожидание квадрата

случайной величины X

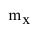    - математическое ожидание случайной величины X

Являясь математическим ожиданием квадрата отклонения от её математического ожидания случайной величины, дисперсия характеризует степень разброса или рассеивание случайной величины около её центра рассеивания. Меньшему значению дисперсии отвечает меньший разброс значений случайной величины относительно её математического ожидания и наоборот.

Рассмотрим некоторые важные свойства дисперсии случайной величины.

1.    Дисперсия постоянной величины с равна О

D[c] = О

2.    При прибавлении к случайной величине X постоянной величины с её дисперсия не изменяется

D[X + c] = D[X]

3.    Дисперсия произведения постоянной величины с на случайную величину равна произведению квадрата постоянной величины на дисперсию случаиной величины:

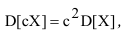
т.е. постоянную величину можно выносить за знак дисперсии, возведя её в квадрат.

Дисперсия имеет размерность квадрата случайной величины и может быть целой, дробной, но всегда положительной.

Размерность квадрата случайной величины приводит к некоторым неудобствам для характеристики случайной величины. Поэтому для большей наглядности целесообразно иметь такую характеристику рассеивания случайной величины, которая имела бы ту же размерность, что и сама случайная величина. Для этого из дисперсии извлекают квадратный корень, а полученную числовую характеристику называют среднеквадратическим отклонением (или «стандартом») случайной величины (обозначают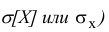

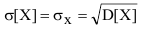
Среднеквадратическое отклонение обладает теми же свойствами, что и дисперсия, однако, вследствие того, что дисперсия есть математическое ожидание квадрата центрированной случайной величины, то при умножении случайной величины X на неслучайную величину с, её среднеквадратическое отклонение умножается на абсолютное значение этой случайной величины:

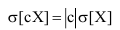
Заключение по лекции:

В лекции мы рассмотрели принципиальные вопросы теории вероятностей применительно к числовым характеристикам случайных величин, ввели основной понятийный аппарат, необходимый для дальнейшего изучения дисциплины: математическое ожидание и дисперсии случайной величины, а так же среднеквадратического отклонения.