Основные законы динамики в теоретической механике

Содержание:

Основные законы механики Галилея — Ньютона:

Динамикой называют раздел теоретической механики, в котором изучают механическое движение в связи с силами, приложенными к движущимся объектам

Предмет динамики

Динамика является основным и наиболее общим разделом теоретической механики. Если в статике мы изучали условия равновесия твердого тела, совершенно не занимаясь вопросами движения, а в кинематике, напротив, изучали движение тел без учета сил, приложенных к этим телам, то в динамике нас будут одинаково интересовать и силы, действующие на материальные тела, и движение этих тел.

В динамике изучают зависимость между движением материальных объектов и действующими на них силами, по данному движению точки или тела устанавливают, какие силы его производят, и по действующим силам определяют движение материального объекта. Поэтому динамика не может, подобно кинематике, ограничиться добавлением к понятиям геометрии одного лишь понятия времени. Она дополняет понятия кинематики понятием силы, известным нам из статики. Нас не интересует физическая сущность силы, и здесь, как и в статике, мы характеризуем силу величиной, направлением и точкой приложения, разве лишь с тем добавлением, что в динамике чаще, чем в статике, рассматривают силы, переменные по величине и направлению.

Две одинаковые силы, приложенные к двум различным материальным телам, могут сообщить этим телам за одно и то же время совершенно различные движения, что зависит от инертности этих тел. Движущиеся объекты характеризуются также и массой и распределением массы. В динамике изучают движение только материальных тел (или точек), обладающих определенной массой.

Таким образом, динамикой называют раздел теоретической механики, в котором изучают механическое движение материальных объектов в связи с силами, приложенными к этим объектам.

В основе динамики лежат три закона Ньютона: 1) принцип инерции, 2) основной закон динамики, 3) принцип равенства действия и противодействия

Три закона движения

В основе всей механики, в частности динамики, лежат три закона, называемые основными законами Галилея—Ньютона и сформулированные Ньютоном под названием «Аксиомы, или законы движения». Они опубликованы в сочинении Ньютона «Математические начала натуральной философии» (1686).

C двумя из этих законов (с первым и третьим) мы ознакомились в курсе статики (см. § 3). Но необходимо обратить внимание на некоторые обстоятельства, которые в динамике имеют большое значение. Поэтому, приступая к курсу динамики, мы критически рассмотрим первую аксиому Ньютона, затем изучим вторую аксиому, а потом расширим наше знакомство с третьей аксиомой.

Систему отсчета, по отношению к которой всякая материальная частица под действием взаимно уравновешенных сил совершает прямолинейное и равномерное движение, называют инерциальной системой отсчета

Инерциальная система отсчета

Первый основной закон механики (принцип инерции) сформулирован Ньютоном так: «Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменять это состояние».

Проверить принцип инерции прямым и непосредственным экспериментом вряд ли можно. Для такого эксперимента понадобилось бы тело, на которое не действуют никакие силы; это тело должно быть полностью изолировано от всех других тел. Никакое тело,, никакая материальная система во Вселенной не являются полностью изолированными. Но ввиду громадности расстояний до звезд можно допустить, что звезды не оказывают заметного действия на солнечную систему, т. е. на систему, состоящую из Солнца, планет и их спутников. Полагают, кроме того, что эта система не подвержена никаким другим посторонним воздействиям, как, например, сопротивление среды, заполняющей мировое пространство. Тогда можно считать, что центр масс (центр тяжести) солнечной системы в данное время находится в состоянии равномерного прямолинейного движения. Центр масс солнечной системы почти совпадает с центром Солнца, и в дальнейшем мы будем называть его центром Солнца.

Возникает вопрос: по отношению к какой системе отсчета центр Солнца движется прямолинейно и равномерно? Вполне конкретно и однозначно ответить на этот вопрос невозможно. Ньютон ошибочно полагал, что независимо от материи существует абсолютно неподвижное пространство. «Абсолютное пространство по самой сущности безотносительно к чему бы то ни было внешнему остается всегда одинаковым и неподвижным», —писал он в «Математических началах натуральной философии». Но мы не мыслим пространства безотносительно к внешнему миру, и для нас пространство есть форма существования материи. Материя же немыслима без движения, поэтому не может быть и пространства, которое было бы абсолютно неподвижно безотносительно к чему бы то ни было, т. е. не может быть неподвижной пустоты. Д’Аламбер, критикуя Ньютона за то, что он понятия пространства и времени отрывал от понятия материи, писал в 1759 г.: «Те философы, которые хотят создать пустоту, теряются в собственных выдумках».

В этом вопросе воззрения Д’Аламбера близко подходят к позиции Энгельса, который писал: «Разумеется, обе эти формы существования материи (т. е. пространство и время—М. Г.) без материи суть ничто, пустые представления, абстракции, существующие только в нашей голове» 1 2 3.
Лобачевский показал, что представления геометрии Эвклида и механики Ньютона о пространстве не являются истинными, и подготовил почву для развития современных физических представлений о пространстве и времени.

Не следует думать, что неправильное понимание Ньютоном абсолютного пространства делает его законы неверными и неприемлемыми. Неправильно только было бы считать аксиомы очевидными истинами, абсолютно верными и не нуждающимися в доказательствах, о чем мы уже говорили в § 3. Аксиомы нуждаются не только в доказательствах, но также и в уточнениях.

Представим себе какую-либо систему координат (связав ее, например, со звездами), по отношению к которой центр Солнца совершает равномерное и прямолинейное движение с какой-либо скоростью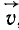

Представим себе также вторую систему координат, совершающую поступательное движение относительно первой системы. Пусть одна из точек (а значит, и все остальные) второй системы движется относительно инерциальной прямолинейно и равномерно с какой-либо скоростью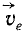

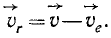    (103')

В правой части равенства мы имеем разность постоянных величин, следовательно, постоянна и левая част равенства, т. е. центр Солнца относительно второй системы координат тоже находится в прямолинейном и равномерном движении. Таким образом, характер движения центра Солнца по отношению к обеим системам координат один и тот же—прямолинейное и равномерное движение. Поэтому и вторую систему координат мы можем называть инерциальной системой, как и всякую прочую систему координат, движущуюся относительно первой поступательно, прямолинейно и равномерно.

В таком движении по отношению ко всякой инерциальной системе находится не только центр солнечной системы, на которую, по нашему заключению, не действуют извне никакие силы, но и каждая материальная частица, находящаяся под действием взаимно уравновешенных сил, потому что наличие взаимно уравновешенных сил эквивалентно их отсутствию (см. § 3). Все это требует значительно расширить понятие «инерциальная система» и определить ее как такую систему отсчета, по отношению к которой всякая материальная частица, находящаяся под действием взаимно уравновешенных сил, совершает прямолинейное и равномерное движение. Любую такую систему можно принять за неподвижную при решении задач динамики. В этом заключается открытый Галилеем так называемый принцип относительности классической механики.

В целом ряде проблем, например в задачах небесной механики — при вычислении траекторий искусственных спутников, при исследованиях, связанных с движением нашей планеты (опыты Фуко), и др., за инерциальную систему принимают систему координат, начало которой находится в центре Солнца, а оси направлены на какие-либо три «неподвижные» звезды. Чтобы показать, как незначительна погрешность, которую допускают, считая звезды неподвижными друг относительно друга, представим себе модель звездного мира, сделанную в масштабе 1:1000000000 000. В таком масштабе наше Солнце, диаметр которого 1500 000 км, изобразится шариком с булавочную головку диаметром 1,5 мм. На расстоянии 15 см от этого шарика будет кружиться невидимая глазу пылинка—Земля. Другие же звезды, в среднем такие же булавочные головки, мы должны будем поместить километров на 40 от Солнца и друг от друга. Если принять скорость Солнца относительно соседних звезд равной 150 км/сек, то, следовательно (в том же масштабе), модель Солнца (начало координат) движется со скоростью 1 мм/ч. Таким образом, относительные перемещения звезд ничтожны, и систему отсчета, связанную со звездами, можно принимать за инерциальную с большой степенью точности.

При многих технических расчетах можно принимать за неподвижную всякую систему отсчета, неизменно связанную с Землей.

Всякую систему координат, неподвижную относительно Земли, обычно принимают за инерциальную систему отсчета, пренебрегая движением Земли вокруг Солнца и вокруг оси. Конечно, при этом допускают некоторую ошибку, потому что невозможно, чтобы принцип инерции был верен одновременно и по отношению к осям, направленным на звезды, и по отношению к осям, участвующим в движении Земли. Но эта ошибка невелика и вполне может быть допущена в обычных технических задачах.

Еще Галилей, который до Ньютона был знаком с принципом инерции, проделал для проверки этого принципа такой интересный опыт. Он катал тяжелые шары вверх по наклонной плоскости, сообщая им одинаковую начальную скорость, и установил, что шары достигали всегда одной и той же высоты h независимо от угла наклона плоскости. Таким образом,

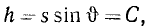
где s-путь, пройденный шаром, а 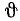— угол между наклонной и горизонтальной плоскостями. Отсюда следует, что при 0∙ = 0 шар должен двигаться непрерывно с сообщенной ему начальной скоростью. Галилей в 1638 г. писал: «Пусть мы метнули или бросили тело по горизонтальной плоскости, устранивши все препятствия. Его движение будет продолжаться равномерно и непрерывно по означенной плоскости, если она простирается неопределенно далеко».

Благодаря этим простым опытам Галилея, проведенным над шарами, катящимися с трением в воздушной среде, принцип инерции получил хотя и косвенное, но прекрасное экспериментальное подтверждение. Однако Галилей неправильно допускал, что возможно инерциальное движение и по окружности. Принцип инерции в инерциальной системе отсчета вполне строго впервые был сформулирован  Декартом.

Ускорение точки пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Основной закон динамики

Из принципа инерции следует, что всякое изменение скорости происходит только от действия сил, приложенных к данному телу. Соотношение между силой и ускорением установлено в основном законе динамики.

Ньютон писал, что изменение скорости «всегда происходит по тому же направлению, как и производящая его сила», независимо от того, находилось тело в покое или в движении и действует сила по скорости, против скорости или же под углом к ней. Хотя Ньютон называл материальную точку телом и не употреблял термина «ускорение» (вошедшего в науку почти два века спустя), но открытый им основной закон динамики можно сформулировать такими словами: сила, действующая на материальную точку, сообщает ей ускорение, пропорциональное силе и направленное по силе. Математически этот закон можно записать в виде такой формулы:

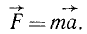     (123)

Если на материальную точку действует несколько сил, то действие каждой из сил не зависит от действия остальных и каждая из сил сообщает точке такое ускорение, какое она ей сообщила бы, если бы действовала одна, а под действием нескольких сил точка получает ускорение 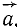 какое получила бы под действием их равнодействующей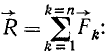 

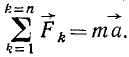     (123')

В этом заключается принцип независимости действия сил.
Величина m в формуле (123') не является только коэффициентом пропорциональности между силой и ускорением, а имеет большой физический смысл, к пояснению которого мы сейчас переходим.

Массой материальной частицы называют меру ее инерции, численно выражающуюся отношением модулей силы, действующей на частицу, и вызванного ею ускорения.

Масса

Всякая материальная частица стремится сохранить свое состояние покоя или прямолинейного и равномерного движения. Свойство материальных тел сохранять механическое движение при отсутствии механического взаимодействия их с другими телами, присущую материи неуничтожаемость движения называют инерцией. Это же свойство инерции побуждает различные тела при одинаковых механических взаимодействиях изменять механическое движение постепенно и различно для каждого тела. Камень притягивается Землей и притягивает к себе Землю с силой такой же величины. Однако эти равные по величине силы вызывают в камне и в Земле далеко не одинаковые ускорения, потому что инерция земного шара, его свойство сохранять свое движение во много миллиардов раз превосходит инерцию камня. Таким образом, в формуле (123) величина m — не только коэффициент пропорциональности, она представляет собой меру инерции материальной точки и выражает ее массу. Итак, масса материальной частицы является мерой инерции материальной частицы, выражающейся положительной скалярной величиной, равной отношению величин силы, приложенной к материальной частице, и ускорения, полученного ею в инерциальной системе отсчета:

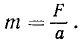     (124)

В частности, все свободно падающие на Землю тела получают под действием силы тяжести G ускорения g свободно падающих тел:

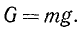
Отсюда, приняв Землю за инерциальную систему отсчета, получаем легкий способ определения массы тел по их весу согласно формуле

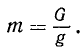     (124')

Все тела, находящиеся в одном и том же месте Земли, падают на Землю с одинаковым ускорением g, из чего следует, что веса тел, находящиеся в одном и том же месте Земли, пропорциональны их массам и не зависят от формы тел. Однако еще во времена Ньютона точные эксперименты показали, что ускорение падающего тела и вес его на экваторе меньше, чем в наших широтах, хотя масса остается прежней. Поэтому Ньютон четко разграничил понятия массы и веса. Открытие Ньютоном закона всемирного тяготения придало различию между массой и весом особо важное значение. Космонавт, летящий вдали от Земли в кабине космической ракеты, почти полностью теряет свой вес, но сохраняет свою массу.

Мы рассматриваем тело как состоящее из отдельных частиц, и, следовательно, масса тела состоит из масс его частиц. Необходимо, однако, учесть, что при движении твердого тела различные частицы совершают, вообще говоря, различные движения и имеют различные ускорения, а потому мера инерции материального тела зависит не только от масс его частиц, но и от их распределения в теле. Только при поступательном движении тела, когда ускорения всех его частиц одинаковы, масса тела является его мерой инерции.

Существуют две системы механических единиц: 1) техническая, в которой за основные приняты единицы длины, силы и времени, и 2) физическая, в которой за основные приняты единицы длины, массы и времени.

Системы механических единиц

Напомним, что в механике приняты две системы единиц: техническая и физическая. Эти две системы отличаются друг от друга по своей основе.

Техническая система единиц построена на понятиях длины L, силы F и времени Т. За основные единицы принимают: длины — метр (м), силы — килограмм-сила (кГ), времени—секунда (сек), но с равным правом применяют также единицы, являющиеся кратными и дольными основных. При решении задач не имеет принципиального значения, какие именно размеры единиц L, F и T приняты в той или иной задаче, это зависит от нашего выбора, и нужно выбирать такие единицы, в которых практически проще можно провести необходимые математические подсчеты. Так, если балка прогибается на несколько миллиметров под нагрузкой в несколько тонн, то, по-видимому, в данном случае выгодно принять миллиметр за единицу длины и тонну-силу за единицу силы, выражать же их в сантиметрах и в граммах или в метрах и килограммах вряд ли целесообразно. Скорость света измеряют километрами в секунду, скорость звука — метрами в секунду, а скорость осадки зданий — миллиметрами в год.

В каждой задаче каждую из единиц мы вправе выбирать основной, кратной или дольной независимо от выбора двух других. Но коль скоро эти единицы нами приняты при решении данной задачи, мы не должны допускать при ее решении никаких других единиц н обязаны брать единицы производных величин, исходя из тех, которые мы выбрали для L, F, Т. Так, приняв в задаче за единицы длины, силы и времени метр, грамм-силу и секунду, мы обязаны принять ускорение свободно падающего тела g = 9,81 м/сек² и было бы ошибкой принять в этой задаче g = 981 см/сек².

В технической системе единиц размерность массы является производной: [m] = L^-1F¹T². Например, размерность единицы массы в технической системе единиц может быть Г ^. сек²/см, если мы выражаем в этой задаче длину в см, силу—в Г, время — в сек.

Неудобство этой системы состоит в том, что единица силы является величиной, требующей указания определенного места земного шара (например, килограмм—вес одного литра воды в Париже при 40^оС, или сила, с которой Земля притягивает массу в 1 кг на широте 45° на уровне моря при нормальном давлении).

Oт этого неудобства можно избавиться, как показал еще Гаусс, если в качестве основных принять единицы длины L, массы M и времени T и вывести единицу силы как производную из этих основных.

Система механических единиц, называемая физической, принимает за основные, кратные и дольные такие же единицы длины (метр, сантиметр и пр.), такие же единицы времени (секунда, минута, час и пр.), но принимает массу, а не силу, за основную единицу (килограмм, а также кратные и дольные килограмм-массы). В этой системе единиц сила является величиной производной и имеет размерность [F] =L¹M¹T^-2, например г ^. см/сек².

В СССР в качестве государственного стандарта принята .Международная система единиц (СИ) (Sl от Le systeme international d’unites), в которой за основные приняты единицы длины, массы и времени. Таким образом, в области механики СИ относится к системе единиц, которую мы назвали физической системой. В качестве основных единиц этой системы в механике оставлены прежние единицы: метр (м), килограмм-масса (кг) и секунда (сек). C целью уточнения метр измерен не в долях земного меридиана, как это было при его установлении, а длиной волны излучения атома криптона, секунда определена как 1/31556925,9747 часть тропического года1, а килограмм — как масса прототипа килограмма, хранящегося в Международном бюро мер и весов в Париже.

Единица силы в СИ является производной. Ньютоном называют силу, сообщающую массе в 1 кг ускорение, равное 1 м/сек². Размер этой единицы силы 1 кг^. м/сек².

Таким образом,
1 н =100 000 дин = 1/9,81 κΓ=102Γ и 1 κΓ = 9,81 н.

Задача:

Автомобиль весом G = 1000 кГ во время разгона движется по прямолинейному горизонтальному пути согласно закону x = O,lt³, где t -время, считаемое от начала движения и выраженное в секундах, а х — путь, пройденный автомобилем за время t, выраженный в метрах. Определить в ньютонах равнодействующую всех сил, действовавших на автомобиль в конце 20-й секунды.

Решение:

Условие задачи дано в технических единицах (L—в м, F—в кГ и T— в сек.), но силу требуется определить в ньютонах. Будем решать задачу в физических единицах и примем L в м, M — в кг и T — в сек. Тогда масса автомобиля m=1000 кг, остальные величины остаются без изменения.
Написав кинематическое уравнение движения

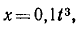
продифференцируем его дважды по времени и найдем ускорение точки:

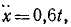
или через 20 сек после начала движения х = 12 м/сек². Умножая на массу, находим силу в ньютонах: F = 1000 ^. 12= 12000 н. 

Если решать задачу в технической системе единиц, предложенной в условии задачи, то в этой системе

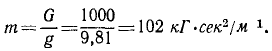
Умножая на ускорение х=12 м/сек², найдем силу

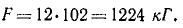
Чтобы выразить ее в ньютонах, надо умножить 1224 на 9,81.
Ответ. F =12000 н.

Системой материальных точек называют мысленно выделенную определенную совокупность материальных частиц или тел, взаимодействующих друг с другом по закону равенства действия и противодействия

Система материальных точек

Принцип равенства действия и противодействия нам хорошо известен еще из статики, где мы им часто пользовались для определения давления тела на опоры: мы составляли уравнения равновесия сил, действующих на данное тело, и определяли реакции опор, а затем уже, пользуясь принципом равенства действия и противодействия, определяли искомые давления тела на опоры, хотя эти давления и не входили в уравнения равновесия твердого тела.

В задачах динамики тот же принцип равенства действия и противодействия приобретает еще и иное значение. Дело в том, что в геометрической статике изучают силы, приложенные только к одному абсолютно твердому телу, под которым понимают такую материальную систему, расстояния между точками которой остаются неизменными. В динамике наряду с абсолютно твердыми телами изучают также и изменяемые системы, т. е. такие системы, расстояния между точками которых могут изменяться под действием сил.

Руководствуясь соображениями удобства решения задачи, мы выделяем некоторое количество тел или частей тела и принимаем их за систему материальных точек. При исследовании движения точек материальной системы необходимо учитывать, что эти материальные точки взаимодействуют между собой по закону равенства действия и противодействия. Таким образом, под системой материальных точек мы понимаем мысленно выделенную совокупность материальных частиц или тел, взаимодействующих друг с другом по закону равенства действия и противодействия. Систему материальных точек иногда коротко называют материальной системой, или механической системой.

Число n точек в системе может быть любым целым числом, большим единицы.

Силы, действующие в материальной системе, подразделяют на внутренние и внешние или на активные и реакции связей

Классификация сил

В динамике, как и в статике, приступая к решению каждой задачи, мы должны в первую очередь определить материальную точку, или абсолютно твердое тело, или материальную систему, движение которой надо исследовать в этой задаче. В очень многих случаях вторым вопросом при постановке задачи бывает вопрос о том, какие силы действуют на эту точку, тело или систему точек.
Силы, действующие на точки материальной системы, часто разделяют на две категории: внешние и внутренние силы.

Внешними силами системы материальных точек называют силы, действующие на точки этой системы со стороны других материальных объектов, не входящих в состав этой системы. Внешние силы обозначают Fe (буква е является начальной буквой латинского слова exterior—внешний) и их проекции X^е, Y^e, Z^e.

Внутренними силами системы называют силы взаимодействия между точками этой системы. Для обозначения внутренних сил и их проекций к соответствующим буквам приписывают сверху и справа букву i (от латинского interior—внутренний), например Fⁱ, Xⁱ.

Одна и та же сила может быть внешней или внутренней в зависимости от того, какие тела мы включили в систему материальных точек. Так, например, давление пара на поршень паровой машины является внешней силой по отношению к поршню и внутренней силой по отношению ко всей паровой машине. Другой пример: велосипедист давит ногой на педаль велосипеда; если за материальную систему принят велосипед, то сила эта внешняя, если же за систему принят велосипед вместе с велосипедистом, то та же сила — внутренняя.

Такое подразделение сил системы на внешние и внутренние полезно в том отношении, что в некоторых общих теоремах динамики (см. § 42 и 44) оказалось возможным исключить внутренние силы и получить зависимости движения только от внешних сил.

Если точки системы свободны., т. е. если движения точек системы не ограничены связями, то силы системы обычно подразделяют на внешние и внутренние. В тех же случаях, когда точки системы несвободны, т. е. их движения ограничены связями, иногда оказывается более целесообразным разделять силы системы на две категории по совершенно иному признаку — на активные силы и реакции связей.
Понятие реакции связей хорошо знакомо нам из курса статики. Этим же понятием мы будем пользоваться и в динамике, с тем лишь добавлением, что в динамике реакции связей зависят от движения системы. Мы будем обозначать реакцию связей и ее проекции F^r, X^r, Y^r, Z^r.

Все прочие силы системы, кроме реакций, будем называть активными силами и отмечать индексом a: F^a, X^a.

Всякая сила является активной или реакцией связи по своей природе, независимо от того, какие точки мы включили в данную материальную систему. Так, давление ноги на педаль является активной силой, а давление педали на ногу—реакцией, независимо от того, принят за систему один велосипед или велосипед с велосипедистом.

Некоторые исторические сведения о развитии динамики

Научные принципы классической механики заложены Галилеем и сформулированы Ньютоном

Возникновение динамики. Как уже было сказано в общем очерке развития теоретической механики, динамика возникла в XVII в. в связи с потребностями быстро развивающейся промышленности, судоходства, а также в связи с возникновением артиллерии.

Развивая работы Галилея и отчасти Гюйгенса, англичанин Исаак Ньютон создал основы теоретической механики и опубликовал их в своем сочинении «Математические начала натуральной философии». Во введении к этой книге, обыкновенно называемой «Начала», сформулированы аксиомы, или законы движения, которые легли в основание всей механики, называемой теперь механикой Галилея — Ньютона, или классической механикой.

Галилей первый (1638 г.) обнародовал закон инерциального движения тел. Этот закон Галилея Ньютон (1686 г.) сформулировал в более общей форме, приведенной нами в § 3 и 36, и назвал первым законом механики.
Галилей открыл (1589 г.) законы падения тел на Землю. Ньютон пришел к общему понятию движения с переменной скоростью. К этому он присоединил очень трудное и важное для динамики понятие массы. Соотношение между изменением движения и силой сформулировано им во втором законе.

Следующий важнейший принцип, лишь слабые и неясные высказывания которого намечались до Ньютона, был сформулирован им под именем третьего закона в форме.

«Мы находим, что механическое движение действительно обладает двоякой мерой, но убеждаемся также, что каждая из этих мер имеет силу для весьма определенно ограниченного круга явлений» (Энгельс)

Спор о mυ и mv²

Как только начала создаваться динамика, сейчас же появилась потребность в определенной мере для измерения движения. Такие меры уже намечались в работах Галилея. Декарт признал произведение массы движущегося тела на его скорость mυ единственной мерой механического движения, назвав эту меру количеством движения. Декарт, как известно, сделал гениальную догадку о сохранении движения (1644 г.). Он считал, что сохраняется именно то, правда, не отличая четко массы от веса.

Напротив, Гюйгенс в своих работах пользовался, и очень успешно, произведением массы на квадрат скорости.

Этим открытием Гюйгенса и утверждением Паскаля, что одно и то же—поднять сто фунтов воды на один дюйм или один фунт на сто дюймов, воспользовался Лейбниц, написав, что декартова мера mυ противоречит декартову закону сохранения движения. Лейбниц доказывал, что сохраняется mυ², а не ти. Тот факт, что mυ² не сохраняется при ударе неупругих тел (см. § 48), Лейбниц объяснил поглощением движения частицами ударяющихся тел. «Это не противоречит,— писал он,— нерушимой истине сохранения силы в природе. То, что поглощается частицами, не потеряно для общей силы участвующих в движении тел». Лейбниц назвал (1695 г.) эту меру mυ² «живой силой».

Сторонники Декарта выступили в его защиту. Лейбница основательно поддержал Иван Бернулли, опубликовавший в 1724 г. сочинение «Дискуссия о законах передачи движения», удостоенное премии Парижской академии наук по конкурсу, объявленному на эту тему. «.. Загорелся знаменитый, длившийся много лет спор, в котором принял участие в первом своем сочинении «Мысли о правильной оценке живых сил» (1746 г.) также и Кант, хотя он неясно разбирался в этом вопросе»,— пишет Энгельс.

Дебют великого философа был не очень удачен, о чем опубликовал ядовитое четверостишие Лессинг. Эпиграмма вызвана не только слабостью выступления Канта, но и остротой дискуссии, которая расколола ученый мир на два враждебных лагеря.

Приблизительно в это время (1758 г.) М. В. Ломоносов читал свою диссертацию, в начале которой он говорил и об этой дискуссии: «Самые первые начала механики, даже физики, еще находятся в периоде обсуждений, и наиболее выдающиеся ученые этого столетия не могут прийти к соглашению о них. Самым блестящим примерой этого есть величина сил движения, которая согласно одним увеличивается в простом, по другим — в двойном отношении скорости».

Сторонниками меры nιυ были Дени Папен (один из изобретателен паровой машины), Маклорен, Кларк (английский философ, переводивший Ньютона и Декарта), английский математик Валлис, Яков Бернулли, Вариньон, Мариотт, Мерсенн, французский физик Орту де Меран, Вольтер и многие другие, тогда как друг Вольтера маркиза дю Шатле, переведшая Ньютона на французский язык, Лопиталь, Кёниг, Иван Бернулли, академик С.-Петербургской академии Даниил Бернулли, распространивший понятие живых сил на жидкость, Яков Герман, немецкий философ Вольф и многие другие защищали меру mv². Голландский математик и физик Гравезанд вначале был на стороне Декарта, но потом перешел на сторону Лейбница.

Свои соображения высказал и Д’Аламбер (1743 г.), после чего этот великий спор затих, но не потому, что Д’Аламбер убедил споривших, а потому, что спор утомил противников и не видно было ему конца. Ведь спорили о том, чем измеряется механическое движение, что сохраняется в природе—mυ² или mυ. Вот почему Ньютон, вообще отрицавший закон сохранения движения, вовсе не принял участия в споре. Но во времена Декарта и Лейбница еще не знали, что механическое движение может переходить в другие виды движения, хотя, как видно и из приведенной нами цитаты Лейбница, эти мысли уже начали зарождаться. Более определенно о немеханических формах движения высказывался М. В. Ломоносов (1744, 1745).

После того как (в XIX веке), по предложению Кориолиса, «живой силой» стали называть 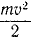, постепенно начала выявляться связь между изменением живой силы и работой.

Четкое толкование понятий обеих мер движения мы находим в «Диалектике природы» Ф. Энгельса. Материальное тело обладает двумя мерами механического движения:

1. живая сила, или кинетическая энергия, характеризует способность механического движения данного тела превращаться в потенциальную энергию пли другие виды движения;
2. количество движения характеризует способность механического
3. движения данного тела передаваться другим материальным телам в виде механического же движения.

В каждом движущемся теле обе меры механического движения существуют одновременно и не противоречат одна другой. Мы подробно остановимся на этом вопросе в главах, посвященных теоремам о количестве движения и теоремам о кинетической энергии.

В задачах динамики несвободных точек и материальных систем большое применение имеют принцип Д’Аламбера и принцип виртуальных перемещений, укоренившиеся в механике в XVIII и XIX вв.

Принцип Д’Аламбера и принцип виртуальных перемещений

В кратких исторических сведениях о проблемах динамики коснемся истории двух принципов динамики: принципа Д’Аламбера и принципа виртуальных перемещений.

В основном законе динамики Ньютон установил зависимость между силой, действующей на точку, и изменением движения, дав тем самым пути решения задач динамики свободной материальной точки. Здесь возникают трудности только математического характера.

Но оставалась не исследованной динамика несвободных систем, т. е. таких систем, на точки которых наложены связи. Быстрое развитие промышленности и торговли выдвигало все новые требования к теоретической механике; понадобились методы, которые давали бы наибольший практический выход и, в частности, имели бы большее применение к машинам, т. е. как раз в области динамики несвободных систем.

Многие крупные ученые проявляли большое остроумие и находчивость, решая различные частные задачи по движению твердого тела и по движению несвободных точек. Однако необходимо было найти общий метод, который дал бы возможность аналитически выразить действие связей, указать общие принципы решения подобных задач.

Честь создания таких методов выпала на долю Д’Аламбера и Лагранжа.

Д’Аламбер предложил для решения всех задач динамики новый принцип. «Данное правило, — писал он позже в Энциклопедии, — приводит все задачи, относящиеся к движению тел, к более простой задаче о равновесии».

Здесь у Д’Аламбера были свои предшественники (Гюйгенс,Яков Бернулли, Яков Герман). «Однако только Д’Аламбер подошел к этому принципу с более общей точки зрения и придал ему всю ту простоту и плодотворность, на которые только он был способен». Поэтому этот принцип называют принципом Д’Аламбера.

Д’Аламбер усматривал достоинство своего метода и в том, что в нем не были применены такие понятия, как сила: «метафизика этих понятий никогда не станет ясной». Но в формулировку принципа Д’Аламбера позднее были введены понятия не только силы, но итак называемых сил инерции, и была придана та форма, которая приведена нами в § 50.

Пять лет спустя после смерти Д’Аламбера, в 1788 г., в Париже была издана «Аналитическая механика» Лагранжа; второе, значительно дополненное издание вышло в 1811—-1815 гг. Это одно из лучших сочинений по механике, обогатившее ее новыми могучими методами.

В основу статики был положен «принцип виртуальных перемещений», который теперь можно сформулировать так: при равновесии системы сумма работ всех активных сил на всяком виртуальном перемещении (см. § 4) равна нулю. Тот же принцип в соединении с принципом Д’Аламбера был положен в основу динамики, (см. § 51).

Корни принципа виртуальных перемещений уходят в глубокую древность. Довольно общую формулировку принципа для сил тяжести дали Торичелли (1644 г.), Иван Бернулли (1717 г.) и др. Доказательство принципа Лагранжем (1796 г.) является лишь видоизменением доказательства, которое предложил в 1783 г. Лазар Карно. Одновременно с Лагранжем строгое доказательство опубликовал Фурье. Но большая заслуга Лагранжа заключается и в том, что он положил этот принцип в основу всей механики.

В те времена еще не было определено понятие работы силы. Только в начале XlX в. появилось точное определение понятия работы, столь необходимое для принципа виртуальных перемещений и в теореме живых сил. В отдельных механических исследованиях начали применять произведение силы на путь еще в XVlII в. Карно (отец) уже в 1786 г. дал ему даже специальное название «момент активности», Гаспар Монж называл его «динамический эффект», англичанин Юнг употреблял слово «работа» еще в 1807 г. Но окончательное введение в науку термина «работа», и притом в точном, современном нам смысле, четкое установление понятия «работа» принадлежит Понселе и Кориолису, развившим идеи Лазара Карно, Гаспара Монжа и отчасти Луи Навье относительно механической работы. Это большое принципиальное достижение в науке было принято не сразу и оценено по достоинству лишь значительно позже.

Мы коснулись развития только немногих проблем динамики, которые входят в программу по теоретической механике втузов. Поэтому в наш краткий исторический очерк развития динамики не вошли многочисленные работы, выполненные за последнее столетие отечественными и иностранными учеными. Желающим более подробно ознакомиться с историей динамики рекомендуем прочитать следующие труды: Геронимус Я. Л. «Очерки о работах корифеев русской механики» (1952 г.); Григорьян А. Т. «Очерки истории механики в России» (1961 г.); Иш л и некий А. Ю. «Очерки по истории техники» (1955 г.); Космодемьянский А. А. «Очерки по истории теоретической механики в России» (1948 г.); Тюлина И. А., Ракчеев Е. Н. «История механики» (1962 г.); Боголюбов А. Н. «История механики машин» (1964).