Основные фигуры геометрии и их расположение в пространстве с примерами

Содержание:

Данный модуль предназначен для повторения всего того, что рассматривалось в курсе стереометрии в этом учебном году. В мини-конспекте систематизированы и обобщены основные темы курса, условно разбитые на блоки: основные фигуры геометрии и их расположение в пространстве; перпендикуляр и наклонная к плоскости, расстояния и углы в пространстве; сечения и проецирование.

Согласно структуре построения геометрии как науки для нее определены:
Основные фигуры (неопределяемые) - точка, прямая, плоскость.

Аксиомы

I. Принадлежности

• I₁ . Какой бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
• I2. Через любые две точки можно провести прямую, и притом только одну.
• I3. Какой бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

II. Взаимного расположения

• II₁. Из трех точек на прямой одна и только одна лежит между двумя другими.
• II₂​​​. Прямая разбивает плоскость на две полуплоскости.
• II3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
• II4. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

III. Измерения

• III₁. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
• III2. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

IV. Откладывания

• IV₁. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и притом только один.
• IV₂. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и притом только один.
• IV₃. Каков бы ни был треугольник, существует треугольник, равный ему, в заданном расположении относительно данной полупрямой.

V. Параллельности

• V₁. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Следствия из аксиом

1. Через прямую и точку, не принадлежащую ей, можно провести плоскость, и притом только одну.
2. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
3. Через три точки, не принадлежащие прямой, можно провести плоскость, и притом только одну.

Взаимное расположение прямых в пространстве 

Две прямые в пространстве могут:

• пересекаться (если имеют только одну общую точку; если пересекаются под прямым углом, то взаимно перпендикулярны);
• совпадать (имеют две и более общих точек);
• быть параллельными (лежат в одной плоскости и не имеют ни одной общей точки);
• быть скрещивающимися (не лежат в одной плоскости).

Свойства перпендикулярных прямых 

1. Через произвольную точку прямой в пространстве можно провести перпендикулярную ей прямую.
2. Если две пересекающиеся прямые соответственно параллельны двум перпендикулярным прямым, то они также перпендикулярны.
3. Через любую точку пространства, не принадлежащую прямой, можно провести прямую, перпендикулярную данной (см. рис. 5.4, а).
4. Если прямая перпендикулярна одной из двух параллельных прямых и лежит с ними в одной плоскости, то она перпендикулярна и второй прямой (см. рис. 5.4, б).
    

• Свойство параллельности прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
• Признак параллельности прямых. Если две прямые параллельны третьей прямой, то они параллельны между собой.
• Признак скрещиваемости прямых. Если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Взаимное расположение прямой и плоскости в пространстве

Прямая и плоскость в пространстве могут:

• пересекаться (если имеют только одну общую точку; если прямая при пересечении плоскости перпендикулярна произвольной прямой этой плоскости, проходящей через точку пересечения, то прямая перпендикулярна и плоскости);
• быть параллельными (не имеют ни одной общей точки);
• иметь две и более общих точек (прямая принадлежит плоскости).
   

Свойства перпендикулярности прямой и плоскости

1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой.
2. Две прямые, перпендикулярные одной плоскости, параллельны.
    

Свойства параллельности прямой и плоскости

1. Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая также пересекает эту плоскость.
2. Если прямая параллельна плоскости, то через каждую точку, взятую на этой плоскости, проходит прямая этой плоскости, параллельная данной прямой (см. рис. 3.19).
3. Через произвольную точку, которая не принадлежит плоскости, проходит множество прямых, параллельных этой плоскости (см. рис. 3.20).
4. Если прямая параллельна каждой из плоскостей, которые пересекаются, то она параллельна и прямой их пересечения (см. рис. 3.21).
    

• Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым этой плоскости, то она перпендикулярна и данной плоскости.
• Признак параллельности прямой и плоскости. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
   

Взаимное расположение двух плоскостей в пространстве

Две плоскости в пространстве могут:

• пересекаться по прямой (если имеют одну общую точку; две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым (см. рис. 5.31));
• быть параллельными (не имеют ни одной общей точки);
• совпадать (имеют две общие прямые, которые пересекаются; общие три точки, не лежащие на прямой; общую прямую и точку, не принадлежащую прямой).

Свойства перпендикулярности плоскостей

1. Любая плоскость, перпендикулярная линии пересечения перпендикулярных плоскостей, пересекает их по перпендикулярным прямым, которые образуют угол между плоскостями. И наоборот, плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна прямой их пересечения.
2. Если две плоскости взаимно перпендикулярны, то любая прямая, лежащая в одной из них и перпендикулярная их линии пересечения, перпендикулярна второй плоскости.
3. Если две плоскости взаимно перпендикулярны и из произвольной точки одной из них опущен перпендикуляр на вторую, то этот перпендикуляр лежит в первой плоскости.
    

Свойства параллельности плоскостей

1. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
2. Если две параллельные плоскости пересечь третьей, то прямые их пересечения параллельны.
3. Параллельные плоскости, пересекая две параллельные прямые, отсекают на них равные отрезки (отрезки параллельных прямых, находящихся между двумя параллельными плоскостями, равны).
4. Две плоскости, параллельные третьей плоскости, параллельны между собой.
    

• Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
   
• Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым второй плоскости, то эти плоскости параллельны.

Перпендикуляр и наклонная к плоскости, расстояния и углы в пространстве

Перпендикуляр и наклонная
Перпендикуляром, проведенным из данной точки к данной плоскости, называется отрезок, который соединяет данную точку с точкой плоскости и лежит на прямой, перпендикулярной этой плоскости (см. рис. 5.21, в). Конец отрезка, лежащий на плоскости, называется основанием перпендикуляра.

Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, который соединяет данную точку с точкой плоскости и не является перпендикуляром к плоскости. Конец отрезка, лежащий на плоскости, называется основанием наклонной. Отрезок, который соединяет основание перпендикуляра и основание наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

Если из одной точки вне плоскости провести к ней перпендикуляр и наклонные, то:

1. длина перпендикуляра меньше длины любой наклонной;
2. наклонные, имеющие равные проекции, равны между собой;
3. из двух наклонных большую длину имеет та, которая имеет большую проекцию.

Теорема (о трех перпендикулярах)

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и наклонной. И наоборот, если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Углы в пространстве

Меньший из углов, образованных двумя пересекающимися прямыми, называется углом между прямыми. Угол между перпендикулярными прямыми равен 90°. Угол между параллельными прямыми равен 0°. Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся.

Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая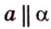

Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.

Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные полуплоскости, образуют линейный угол (см. рис. 6.3).
 

Углом между пересекающимися плоскостями называется угол между прямыми, образованными пересечением этих плоскостей третьей плоскостью, перпендикулярной их линии пересечения. Угол между параллельными плоскостями равен 0°.
 

Расстояния в пространстве

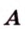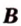Расстоянием между двумя точками и  называется длина отрезка .

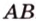Расстояние от точки 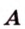до прямой  равно длине перпендикуляра 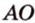, проведенного из этой точки к данной прямой (см. рис. 6.15). Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к плоскости (см. рис. 6.16). Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (см. рис. 6.18).

Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из какой-нибудь точки прямой к плоскости.

Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из какой-нибудь точки одной плоскости ко второй.
 

Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
 

Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Она равна расстоянию между параллельными плоскостями, проходящими через эти прямые.
 

Сечения

Если хотя бы две точки пространственной геометрической фигуры лежат по разные стороны плоскости, то говорят, что плоскость ее пересекает, плоскость называют секущей плоскостью. Фигура, состоящая из всех общих точек геометрической фигуры и секущей плоскости, называется сечением геометрической фигуры.

Прямую, по которой плоскость сечения пересекает плоскость любой грани многогранника, называют следом плоскости сечения. Этим устанавливается количество следов: следов столько, сколько плоскостей граней пересекает плоскость сечения.

При построении сечения следует помнить:

• через две точки, принадлежащие плоскости, проходит только одна прямая, которая принадлежит этой плоскости;
• чтобы построить линию пересечения двух плоскостей, необходимо найти две точки, которые принадлежат обеим плоскостям, и через них провести линию пересечения;
• при построении сечений многогранников секущей плоскостью следует найти отрезки, по которым секущая плоскость пересекается с гранями многогранника.

Проецирование

Чтобы изобразить пространственные фигуры на плоскости, пользуются разными методами. Один из них - параллельное проецирование.
 

Параллельное проецирование - это метод изображения произвольной геометрической фигуры на плоскости, при котором все точки фигуры переносятся на плоскость по прямым, параллельным заданной (направление проецирования). Каждая геометрическая фигура состоит из точек, поэтому, проецируя последовательно точки фигуры на плоскость, получаем изображение — проекцию этой фигуры, а способ выполнения изображения - параллельное проецирование.

Свойства параллельного проецирования для прямых и отрезков, не параллельных направлению проецирования:

1. Проекцией прямой является прямая, а проекцией отрезка - отрезок.
2. Проекции параллельных прямых параллельны или совпадают.
3. Соотношения длин отрезков одной прямой или параллельных прямых сохраняются (см. рис. 4.26), т.е. равны соотношениям длин своих проекций, в частности середина отрезка проецируется в середину его проекции.

Параллельное проецирование, направление которого перпендикулярно плоскости проекций, называется ортогональным проецированием. Для ортогонального проецирования выполняются все свойства параллельного проецирования.

Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади многоугольника на косинус угла между его плоскостью и плоскостью проекции.