Основание метода Монте-Карло - суть, пример и практика

Содержание:

Метод Монте-Карло можно определить как метод моделирования случайных величин для вычисления свойств их распределений. Истоки идеи использования случайных явлений в области приблизительных вычислений можно проследить до 1878 года, когда была опубликована работа Холла по определению числа p путем случайного бросания иглы на бумагу с параллельной подкладкой. По сути, идея заключается в том, чтобы экспериментально воспроизвести событие, вероятность которого выражается числом p, и приблизительно оценить эту вероятность. Отечественные работы по методу Монте-Карло появились в 1955-1956 годах, и с тех пор накопилась обширная библиография по методу Монте-Карло. Даже беглый обзор названий статей позволяет предположить, что метод Монте-Карло применим для решения прикладных задач из широкого круга областей науки и техники.

Первоначально метод Монте-Карло использовался в основном для решения задач нейтронной физики, где традиционные численные методы оказались бесполезными. Позднее его влияние распространилось на широкий класс проблем статистической физики, которые весьма различны по содержанию. Метод Монте-Карло оказал и продолжает оказывать значительное влияние на развитие методов вычислительной математики (например, разработка методов численной интеграции) и успешно комбинируется и дополняется другими вычислительными методами при решении многих задач. Его применение оправдано особенно для тех проблем, которые допускают теоретическое и вероятностное описание. Это объясняется как очевидностью получения ответа с определенной вероятностью в задачах с вероятностным содержанием, так и существенным упрощением процедуры решения.

Метод статистического моделирования

Метод Монте-Карло родился в 1949 году, когда была опубликована статья "Метод Монте-Карло". Основателями этого метода считаются американские математики Дж. Нейман и С. Нейман, а также С. Улама. В СССР первые статьи о методе Монте-Карло были опубликованы в 1955-1956 годах. Интересно, что теоретическая основа метода была известна давно. Более того, некоторые статистические проблемы иногда рассчитывались с использованием случайных выборок, то есть фактически по методу Монте-Карло. Однако до появления электронных компьютеров этот метод не мог широко использоваться, поскольку моделирование случайных величин вручную занимает очень много времени. Таким образом, появление метода Монте-Карло как очень многогранного численного метода стало возможным только с появлением компьютера.

Название "Монте-Карло" происходит от города Монте-Карло в княжестве Монако, которое славится своим игорным домом. Идея метода чрезвычайно проста и заключается в следующем. Вместо того, чтобы описывать процесс с помощью аналитического аппарата (дифференциальные или алгебраические уравнения), можно "нарисовать" случайный феномен с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. В реальности каждый раз конкретное внедрение случайного процесса сочиняется по-разному; также в результате статистического моделирования мы каждый раз получаем новую, иную реализацию исследуемого процесса. Что оно может нам дать? Ничто само по себе, как, скажем, единственный случай, когда пациент вылечился с помощью лекарства.

Совсем другое дело, если мы получим набор таких реализаций. Данный набор реализаций может быть использован как вид искусственно полученного статистического материала, который может быть обработан обычными методами математической статистики. После такой обработки можно получить любые интересующие нас свойства: Событийные вероятности, математические ожидания и дисперсии случайных величин и т.д. Моделируя случайные явления методом Монте-Карло, мы используем сам шанс как исследовательский аппарат и заставляем его "работать на нас". Часто эта техника проще, чем попытка построения аналитической модели. Для сложных процессов с большим количеством элементов (машины, люди, организации, утилиты), где случайные факторы замысловато переплетаются, и где процесс явно немарковский, метод статистического моделирования обычно легче аналитического (и часто является единственным вариантом). По сути, любая вероятностная проблема может быть решена методом Монте-Карло, но это оправдано только тогда, когда процедура рисования проще и не сложнее аналитического расчета. Вот пример, где метод Монте-Карло возможен, но в высшей степени необоснован.

Предположим, по одной цели делается три независимых выстрела, каждый с вероятностью 1/2 попадания в цель. Нужно определить вероятность хотя бы одного попадания в цель. По элементарному расчету вероятность хотя бы одного попадания равна 1 - (1/2)3 = 7/8. Эту же задачу можно решить "кастингом", или статистическим моделированием. Вместо "трех выстрелов" мы бросим "три монеты", считая, например, крест - за попадание, число - за "промах". Опыт считается "успешным", если хотя бы на одной из монет изображен герб. Если мы делаем очень, очень много экспериментов, то подсчитываем общее количество "попаданий" и делим на количество N выполненных экспериментов. Это дает нам частоту события, и это близко к вероятности, если мы проведем большое количество экспериментов. Ну, что? Такой метод мог бы использовать только человек, который вообще не знает теории вероятностей, но в принципе это возможно. Метод Монте-Карло - численный метод решения математических задач путем моделирования случайных величин.

Метод Монте-Карло - это метод моделирования случайных величин для определения свойств их распределения.

Суть метода Монте-Карло

Метод статистического моделирования на компьютере является основным методом получения результатов с использованием имитационных моделей стохастических систем, которые используются в качестве теоретических основ предельных теорем теории вероятностей. Метод Монте-Карло лежит в основе.

Метод Монте-Карло был предложен в 1940-х годах J. Von Neumann и относится к моделированию процессов с помощью генератора случайных величин.

Идея использования случайных явлений для приблизительных расчетов возникла в 1878 г. с появлением бумаги Холла, в которой содержался метод определения p-чисел путем случайного бросания иглы на необрамленную бумагу с параллельными линиями. Идея состояла в том, чтобы экспериментально воспроизвести событие, вероятность которого была выражена с помощью p, и приблизительно оценить эту вероятность.

Первоначально метод Монте-Карло использовался для решения задач нейрофизики, так как традиционные вычислительные методы были малополезны. Затем влияние метода распространилось на проблемы статистической физики, которые были разными по содержанию. Сегодня метод Монте-Карло более широко используется в таких отраслях науки, как наука:

• Теория массовой службы;
• теория игр и математическая экономика;
• теория передачи сообщений в условиях помех и т.д.

Описанный метод оказывает большое влияние на развитие методов вычислительной математики и комбинируется с другими методами вычислений при решении задач. Применение метода оправдано в задачах, допускающих теоретическое и вероятностное описание.

Пример метода

Рассмотрим численный пример метода Монте-Карло: a=0;b=π/2;g(x)=cos(x).

Определим значение интеграла по двум случайным переменным.

В первом варианте используется равномерно распределенная случайная величина на [a,b], т.е. pe(x)=2/π.

Во втором варианте используется случайная переменная с линейной плотностью на [a,b], т.е. pe(x)=4/π-(1-2x/π).

На рис. 1 представлен график вышеуказанных функций.

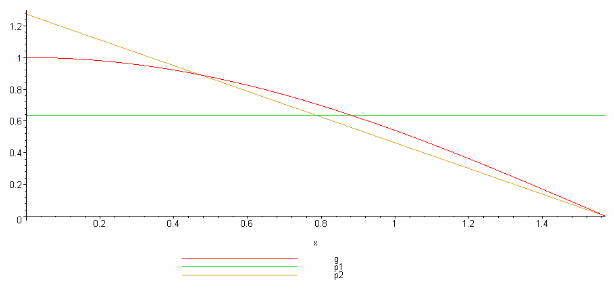
Рисунок 1. функциональный график. 

Нетрудно заметить, что линейная плотность соответствует функции g(x).

Нетрудно вычислить точное значение интеграла и оно будет равно 1.

Для N=10 результаты моделирования выглядят следующим образом:

Для равномерно распределённой переменной I≈1.21666, а для случайной переменной с линейным распределением I≈0.97641.

В первом случае относительная погрешность составляет 21%, во втором - 2,35%.

Данная примерная модель показывает, насколько важным является определение случайной величины для метода Монте-Карло. Если случайная переменная выбрана правильно, то вычисление будет иметь более высокую точность с меньшим количеством подынтегральных значений.

В то время как метод Монте-Карло является средством численного анализа, изучение физических процессов с его помощью позволяет определять их характерные свойства, что позволяет создавать удовлетворительные аналитические модели определенных процессов.

Метод Монте-Карло на практике

Метод Монте-Карло типичен для системного анализа. Его можно использовать для получения приблизительного решения задач на основе эксперимента со случайными числами. Например, необходимо определить вероятность выигрыша в карточной игре. Объем вычислений с использованием метода прямого вычисления будет достаточно большим. В игру также можно играть N раз, после чего можно посчитать количество выигрышей n и определить вероятность, равную соотношению n/N. Этот метод может привести к ошибкам, но их значение уменьшается с увеличением количества игр. Чтобы ускорить расчеты, игру можно смоделировать на компьютере. Однако, чтобы получить точный ответ, число проб может быть большим, при этом величина ошибок медленно уменьшается. Поэтому было бы более полезным совмещать анализ со случайной выборкой. В этом суть метода Монте-Карло.

Метод Монте-Карло является эволюцией методов выборки, используемых в статистике. Отличается тем, что цель этого метода - найти ответы на математические задачи, и все тесты проводятся в абстрактных ситуациях, а не с использованием результатов реальных исследований. Абстракция, позволившая изменить объект исследования, позволила усовершенствовать метод.

Ряд проблем, возникших при разработке ядерного оружия во время Второй мировой войны, был решен методом Монте-Карло. Задача состояла в том, чтобы вычислить количество нейтронов, проникающих в оболочку структуры, предполагая, что это количество может изменяться не только случайным образом, но и в случайном порядке. С помощью метода Монте-Карло на компьютере была воссоздана математическая модель реальной ситуации, а атомные частицы были прослежены с помощью случайных чисел. При изучении реальных проблем диффузии атомных частиц через экран ядерного реактора ученые обязательно моделировали реальные физические процессы. Их не интересовали модели как таковые, но они изучали реальные процессы, которые не могли воспроизвести в жизни. Важной особенностью метода была возможность изменения модели или ее параметров для снижения стоимости вычислений за счет уменьшения количества выборок. Эти математические методы стали известны как средство уменьшения количества вариаций. В этом контексте в настоящее время часто утверждается, что выборочные расчеты не являются методом Монте-Карло до тех пор, пока не будут использоваться средства для уменьшения числа вариаций.

Широкое использование метода в исследованиях операций обусловлено тем, что он является самым простым из всех вычислительных методов, пригодных для решения крупных научных задач.