Ортогональное проецирование - определение и вычисление с примерами решения

Ортогональное проецирование:

Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.

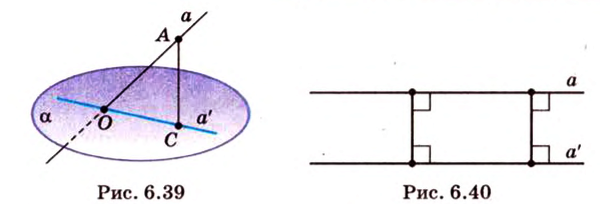
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой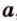

Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.

Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.

Площадь ортогональной проекции

Теорема 5

Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.

Доказательство:

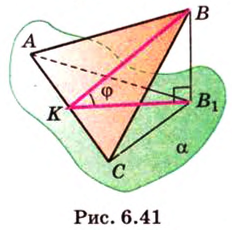
Как пример многоугольника возьмем 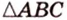(рис. 6.41). Проекцией 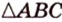на плоскость 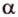является 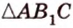. Проведем высоту 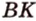треугольника 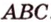. По теореме
о трех перпендикулярах 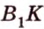- высота 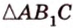. Угол 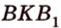- угол между плоскостью 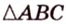и плоскостью проекции. Пусть 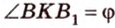. Тогда

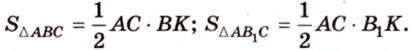
Учитывая, что 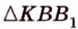прямоугольный 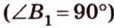, имеем: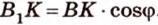. Поэтому

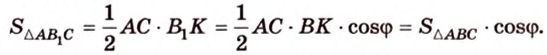
Итак, . Теорема доказана.

Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство

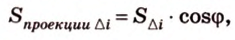
где 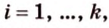поскольку угол между плоскостями этих треугольников и плоскостью их проекций будет один и тот же. Все эти равенства сложим почленно:

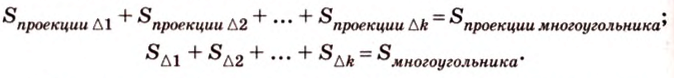
Получим в левой части равенства площадь проекции многоугольника, а в правой - площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда

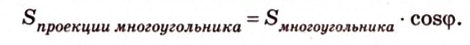
Т.е. и для этого случая теорема истинна.

Пример:

Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.

Решение:

Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:

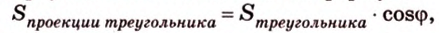
где 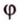 - угол между плоскостью треугольника и плоскостью проекции.
По формуле Герона найдем площадь :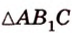

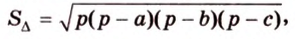
где 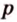- полупериметр треугольника, 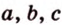- его стороны.

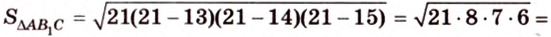
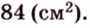
Тогда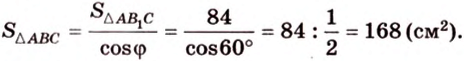

Ответ: 168 см².