Оптика в физике - основные понятия, формулы и определение с примерами

Содержание:

Оптика:

Чем меньше скорость распространения света в среде, тем среда является оптически более плотной.

Оптика — раздел физики, в котором изучаются физическая природа и свойства света, а также его взаимодействие с веществом. Соответственно световые явления часто называют оптическими явлениями. Слово «оптика» произошло от греческого слова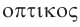

Что такое оптика

По количеству и качеству информации, получаемой человеком об окружающем мире, зрение намного превосходит слух. Этот факт обусловлен существенным различием длин волн видимого света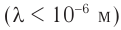 

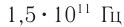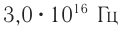Под светом в оптике понимают электромагнитные волны, частоты которых находятся в диапазоне от до . Этот диапазон делится на инфракрасный 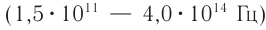, видимый 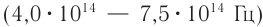и ультрафиолетовый 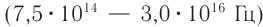диапазоны.

Современная оптика основана на электромагнитной теории света. Как вам известно, во второй половине XIX в. Дж. Максвелл доказал возможность распространения электромагнитных волн в вакууме. Согласно выводам из его теории свет имеет электромагнитную природу, поскольку скорость его распространения равна скорости электромагнитных волн в вакууме.

В 1672 г. английский ученый Роберт Гук в докладе английскому Королевскому обществу высказал гипотезу о том, что свет представляет собой быстро распространяющиеся поперечные волны.

Теорию продольных световых волн разработал голландский физик Христиан Гюйгенс в 1690 г. в «Трактате о свете». Он, исходя из аналогии между акустическими и оптическими явлениями, полагал, что свет как упругие волны распространяется в особой среде — эфире, заполняющем все пространство как внутри материальных тел, так и между ними. В трактате с позиций волновой природы света объяснялось отражение и преломление света.

Первые попытки измерения скорости света на расстоянии нескольких километров, предпринятые Галилео Галилеем и другими учеными, не увенчались успехом в силу недостаточной точности измерения времени (хронометрирования). Из этих экспериментов Галилей сделал вывод, что измерить модуль скорости света на малых расстояниях практически невозможно, поскольку свет преодолевает их мгновенно в силу большого значения скорости распространения.

Рене Декарт одним из первых предложил использовать для измерения модуля скорости света огромные (астрономические) расстояния, на преодоление которых свету потребуется значительное время, которое можно измерять с достаточной точностью.

Исторически первое экспериментальное определение модуля скорости света в вакууме в 1672 г. сделал датский астроном Олаф Рёмер, который проводил систематические наблюдения затмений спутника Юпитера — Ио в телескоп. Примерно через полгода после начала наблюдений он заметил, что момент затмения спутника Ио запаздывает почти на 16 мин по сравнению с вычисленным значением.

Описание экспериментов Рёмера по измерению скорости света Гюйгенс привел в своем «Трактате о свете».

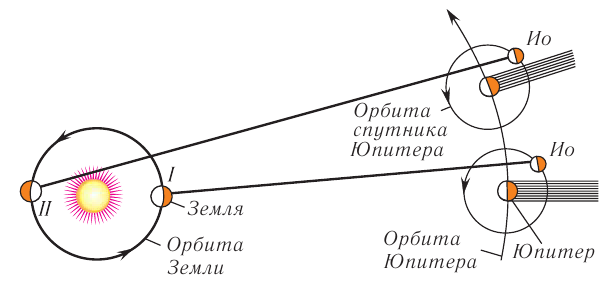
Рис. 50. Схема наблюдений Рёмера

Рёмер объяснил эту задержку конечностью скорости распространения света. Поскольку за полгода Земля переместилась из положения I (рис. 50) в положение II, то надо учитывать время, необходимое для того, чтобы свет прошел добавочное расстояние, примерно равное диаметру земной орбиты.

На основании имевшихся в то время данных о диаметрах орбит Земли и Юпитера он получил для модуля скорости света значение:

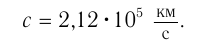
Скорость распространения света в вакууме обозначается латинской буквой 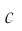(от лат. celeritas — скорость).

Значение модуля скорости света, полученное Рёмером, уточнил французский физик Арман Физо в 1849 г., измерив его лабораторным способом. Полученное им значение модуля скорости света — 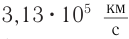.Американский физик Альберт Майкель-сон в 1926 г. для более точного измерения скорости света использовал установку, расположенную между двумя горными вершинами, расстояние между которыми 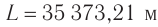. Схема установки изображена на рисунке 51. Зеркалом являлась восьмигранная стальная призма, которая, вращалась с частотой 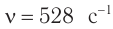. Метод измерения основывался на том, что луч света от источника 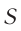может попасть в зрительную трубу 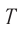только в том случае, если за время его распространения по пути 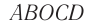стальная призма успеет повернуться на 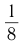оборота (см. рис. 51). Следовательно, измеренное время  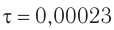с составляло 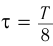, где 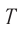— период вращения призмы.

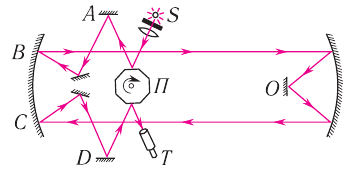
Рис. 51. Схема опыта Майкельсона: 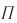— вращающаяся стальная призма; 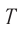— зрительная труба; 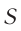— источник света.

Майкельсон получил значение модуля скорости света, близкое к современным данным:

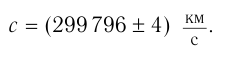
В 1972 г. значение модуля скорости света было определено на основе независимых измерений длины волны и частоты света. Это позволило значительно повысить точность измерений. В качестве источника был выбран гелиево-неоновый лазер. Таким образом, было получено значение скорости света, превосходящее по точности все ранее известные значения более чем на два порядка.

Согласно современным измерениям модуль скорости распространения света в вакууме:

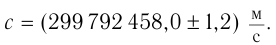
В 1983 г. на заседании Генеральной ассамблеи мер и весов было принято новое определение эталона метра с учетом того, что скорость распространения света в вакууме точно равна .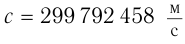

Заметим, что при решении задач используют приближенное значение модуля скорости света: 

Одним из параметров, характеризующих световую волну в вакууме, является длина волны 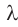, связанная с периодом колебаний 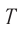соотношением:

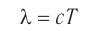
и с частотой 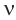соотношением:

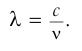
Измерения показали, что модуль скорости света 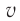в различных веществах всегда меньше, чем модуль скорости света 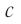в вакууме. В 1862 г. французский физик Жан Фуко измерил модуль скорости распространения света в воде и получил значение 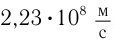. Через несколько лет Майкельсон определил модуль скорости распространения света в сероуглероде — 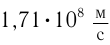. Следовательно, в воде модуль скорости распространения света уменьшается в 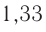раза по сравнению с вакуумом, а в сероуглероде — в 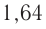раза.

При изучении физики 8-го класса вы узнали, что, чем меньше скорость распространения света в среде, тем среда является оптически более плотной. Мерой оптической плотности вещества является его абсолютный показатель преломления, который обозначается латинской буквой .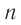

Абсолютный показатель преломления 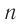вещества характеризует его оптические свойства и показывает, во сколько раз модуль скорости распространения света в данном веществе меньше модуля скорости распространения света в вакууме:

Так как модуль скорости распространения света в любом веществе всегда меньше, чем в вакууме, то абсолютный показатель преломления вещества всегда больше единицы 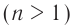. Абсолютный показатель преломления зависит как от свойств вещества, т. е. его химического состава, агрегатного состояния, температуры, давления, так и от частоты света.

Исходя из соотношения (1), можно записать формулу для нахождения модуля скорости распространения света в веществе:

Кроме того, из соотношения (1) следует, что для любых сред

где 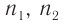— абсолютные показатели преломления сред, 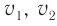— модули скоростей распространения света в средах.

Подставим в соотношение (3) выражение 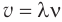, связывающее модуль скорости распространения света 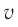в веществе с длиной волны 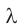и частотой 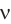. Так как при переходе электромагнитной волны из вакуума в вещество или из одного вещества в другое частота колебаний напряженности 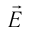электрического поля и индукции 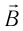магнитного поля не изменяется 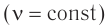, то

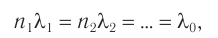
где 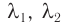 — длины световых волн в средах, 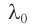— длина волны в вакууме.

Отсюда следует, что длина световой волны 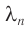при переходе из одного вещества в другое изменяется.

Длина световой волны 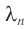в веществе, абсолютный показатель преломления которого 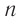, определяется по формуле:

Таким образом, при переходе света из одного вещества в другое частота остается неизменной, а изменяются скорость распространения световой волны и ее длина.

Белый свет представляет собой совокупность электромагнитных волн всевозможных частот видимого диапазона. Волна одной определенной и строго постоянной частоты называется монохроматической (от греч. 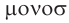(монос) — свет и  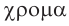(хрома) — цвет, т. е. одноцветный).

Как показали результаты многочисленных экспериментов, световое ощущение у человека вызывают лишь электромагнитные волны видимого диапазона 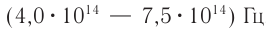, которому соответствуют длины волн от  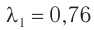мкм до  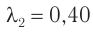мкм, воспринимаемые глазом человека.

Каждой частоте соответствует свое цветовое ощущение. Так, например, свет частотой 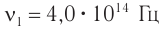вызывает ощущение красного цвета, а 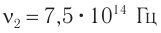— фиолетового. Поскольку цвет волн, воспринимаемых глазом, определяется только частотой световой волны, то при переходах из одного вещества в другое цветовое восприятие не изменяется.

Пример решения задачи:

Монохроматический свет длиной волны 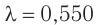мкм переходит из стекла в воздух. Определите, на какое значение 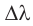увеличивается длина волны света в воздухе, если абсолютный показатель преломления стекла 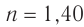. Найдите модуль распространения скорости 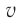света в стекле, если модуль скорости распространения света в воздухе .

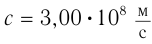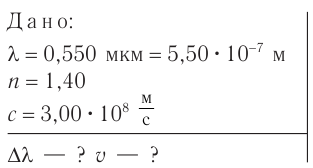
Решение

Учитывая, что частота света не зависит от свойств среды, можем записать:

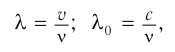
где 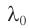— длина волны в воздухе. Поскольку длина волны прямо пропорциональна скорости распространения света, то

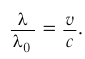
Выражая из последнего равенства 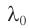, найдем:

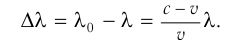
Так как 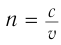, то формулу для 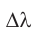можно переписать в виде:

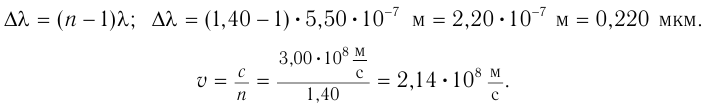
Ответ: .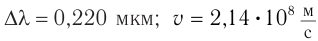

Интерференция света

Принцип суперпозиции электрических полей: напряженность 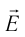электрического поля системы точечных зарядов 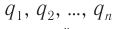в некоторой точке пространства равна векторной сумме напряженностей полей, создаваемых в этой точке каждым из этих зарядов по отдельности, причем поле каждого не зависит от полей других:

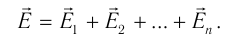
Рассмотрим процесс наложения волн длиной 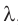, возбуждаемых одинаковыми точечными монохроматическими источниками света 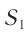и 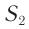(рис. 52). В той области среды, где встречаются две волны от разных источников, происходит их наложение.

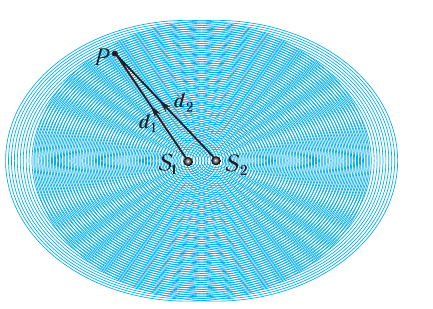
Рис. 52. Процесс наложения одинаковых волн

Согласно принципу суперпозиции (от лат. superposition — добавление) колебания, вызванные волнами, складываются таким образом, что результирующее смещение каждой частицы среды равно сумме отдельных смещений. Причем каждая из волн распространяется независимо друг от друга. Более того, волны свободно проходят сквозь друг друга и при этом никак не взаимодействуют между собой.

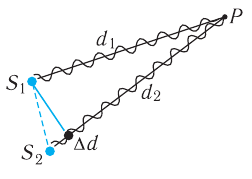
Рис. 53. Схема процесса наложения одинаковых волн

Если в точку 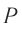от монохроматических источников частотой 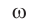пришли две волны, прошедшие разные расстояния 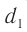и 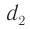(рис. 53), то разность расстояний 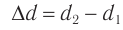, которую называют разностью хода, обусловливает сдвиг по фазе

Следовательно, результат сложения волн зависит от разности фаз 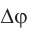между ними, а она определяется разностью хода .

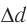Волны одинаковых частот, разность фаз колебаний которых в данной точке пространства не изменяется с течением времени, называются когерентными (от лат. cohaerens — связанный, сцепленный). Соответственно, свойство, характеризующее согласованность протекания в пространстве и времени нескольких колебательных или волновых процессов, называется когерентностью.

Предположим, что приходящие волны будут иметь в точке 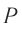 напряженности электрического поля:

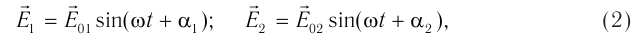
где 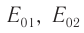— амплитуды, 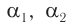— начальные фазы колебаний в каждой из волн соответственно.

Как следует из (2), волны, приходящие в некоторую точку пространства 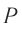, возбуждают в ней гармонические колебания одинаковой частоты, определяемой частотой со источников 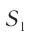и 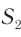. Будем считать, что направления колебаний в каждой из волн одинаковы.

Заметим, что разность фаз колебаний, возбуждаемых рассматриваемыми источниками в точке 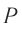, остается постоянной с течением времени, даже если начальные фазы этих колебаний различны.

Амплитуда результирующего колебания согласно принципу суперпозиции в любой момент времени равна векторной сумме амплитуд каждой волны по отдельности. Результирующее колебание представляет собой их сумму:

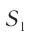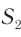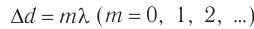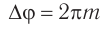Если разность хода волн от источников и  кратна длине волны , то , и колебания, возбуждаемые волнами в точке 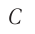(рис. 54, а), происходят в одинаковой фазе.

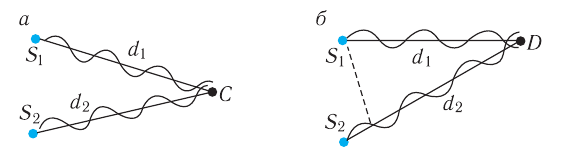
Рис. 54. Сложение монохроматических колебаний двух волн: а — максимальная амплитуда в точке 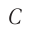, б — минимальная амплитуда в точке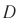

При этом гребень одной волны накладывается на гребень другой. Соответственно, амплитуда результирующего колебания в точке 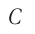равна сумме амплитуд слагаемых волн и оказывается максимальной (рис. 55):

Если же разность хода волн в точке 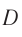(рис. 54, б) равна нечетному числу полуволн

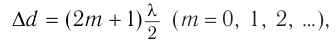
то 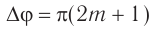, и колебания происходят в противофазе.

При этом гребень одной волны накладывается на впадину другой. В этом случае амплитуда результирующего колебания равна модулю разности амплитуд накладывающихся волн и оказывается минимальной (рис. 56):

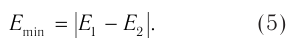
Заметим, что во всех других точках накладывающихся волн амплитуда 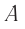результирующего колебания имеет промежуточное значение:

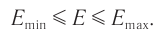
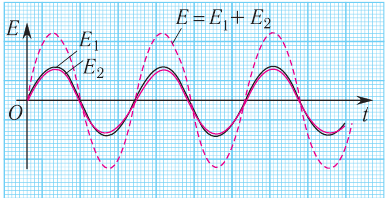
Рис. 55. Сложение амплитуд волн

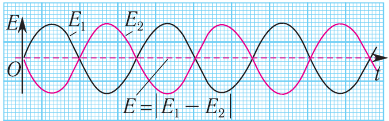
Рис. 56. Вычитание амплитуд волн

Приемники излучения фиксируют не саму световую волну, а энергию, принесенную волной в данную область пространства. Параметром, характеризующим эту энергию, является интенсивность световой волны, которая обозначается латинской буквой 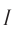. Интенсивность световой волны численно равна средней энергии, которая переносится волной за единицу времени через площадку единичной площади, ориентированную перпендикулярно направлению распространения волны. Согласно волновой теории электромагнетизма интенсивность электромагнитной волны пропорциональна квадрату амплитуды вектора напряженности ее электрического поля 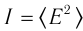. Символ 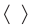означает усреднение по времени.

Таким образом, интенсивность результирующей волны не равна сумме интенсивностей исходных волн. Это означает, что волны интерферируют друг с другом. Вследствие зависимости разности фаз (1) от точки наблюдения, в пространстве получается сложная картина распределения интенсивности результирующей волны. Устойчивое во времени распределение амплитуд колебаний в пространстве при интерференции называется интерференционной картиной.

Интерференция (от лат. inter — взаимно, между собой и ferio — ударяю, поражаю) — явление возникновения устойчивой во времени картины чередующихся максимумов и минимумов амплитуд результирующей волны при сложении двух (или нескольких) когерентных волн.

Закономерности интерференции волн справедливы для волн любой природы (рис. 57), т. е. носят универсальный характер.

При рассмотрении интерференции света (электромагнитных волн) следует учесть, что длина волны света в веществе изменяется в зависимости от показателя преломления вещества. Если одна волна распространяется в веществе с показателем преломления 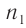, а другая — с показателем преломления 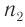, то разность фаз колебаний

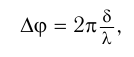
где

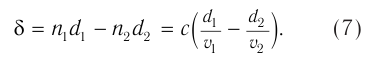
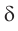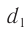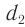Здесь — оптическая разность хода волн от источника до точки наблюдения. Эта величина определяется расстояниями и , пройденными волнами с учетом их различных скоростей распространения  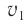и 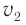 в этих средах с показателями преломления  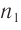и .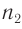

Рис. 57. Интерференционная картина поперечных волн на поверхности воды

Таким образом, если оптическая разность хода (7) равна целому числу длин волн:

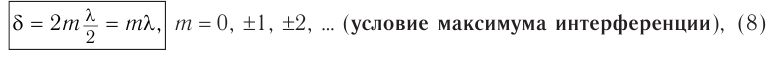
то волны приходят в точку 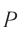 (см. рис. 53) синфазно, поскольку разность фаз в этом случае кратна .

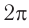Действительно:

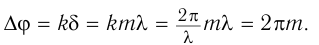
Если оптическая разность хода (7) равна нечетному числу полуволн:

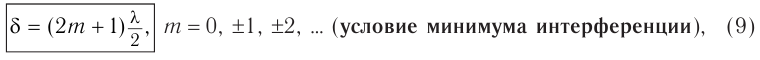
то волны приходят в точку 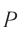в противофазе. Разность фаз колебаний в этом случае равна:

Для наблюдения интерференции света необходимы когерентные источники, излучающие волны с фиксированной разностью фаз. Распространенные обычные источники света (лампы накаливания, лампы дневного света, свечи и т. д.) не являются когерентными. Для того чтобы можно было наблюдать от них интерференцию света, свет от одного и того же источника необходимо разделить на два пучка и затем свести их вместе.

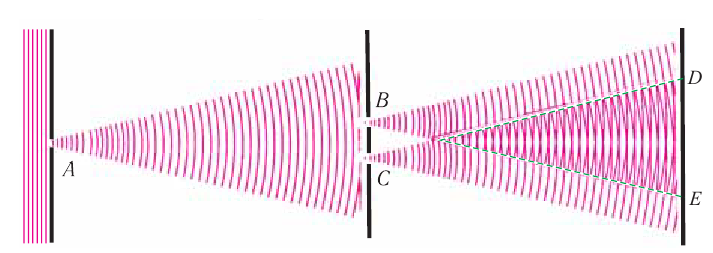
Рис. 58. Схема эксперимента Юнга по интерференции света

Для получения интерференционной картины пользуются классической интерференционной схемой (схемой Юнга), где пучок света от небольшого отверстия 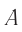 в ширме разделяется на два когерентных пучка с помощью небольших отверсти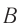й и 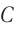в следующей ширме (рис. 58). Поскольку эти пучки созданы одним и тем же источником 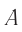, они являются когерентными. Поэтому на экране в области перекрытия пучков 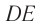наблюдается интерференционная картина.

Классический эксперимент по наблюдениям интерференции света английский  ученый Томас Юнг провел в 1801 г. Это позволило измерить длину световой волны и убедительно подтвердить волновую природу света.

Изобретение и распространение когерентных источников излучения — лазеров — сделало демонстрацию явления интерференции достаточно простой.

Отметим еще один распространенный случай интерференции — сложение волн одинаковой частоты, распространяющихся в противоположных направлениях (например, падающей и отраженной волн). Это приводит к образованию в пространстве устойчивой картины чередования максимумов амплитуды колебаний (пучностей) и минимумов (узлов) (рис. 59). Волна, возникающая в результате сложения двух волн одинаковой частоты, распространяющихся в противоположных направлениях, называется стоячей волной.

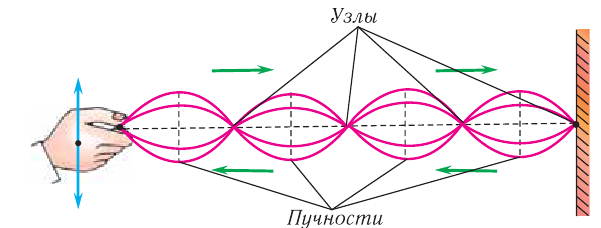
Рис. 59. Стоячая волна

Пример №1

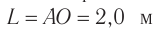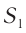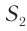Рассчитайте положения максимумов и минимумов интерференционной картины на экране, находящемся на расстоянии от двух одинаковых когерентных источников света и , которые расположены в вакууме на расстоянии 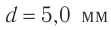друг от друга (рис. 60). Длина волны излучения источников 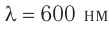. Найдите расстояние 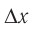между соседними максимумами.

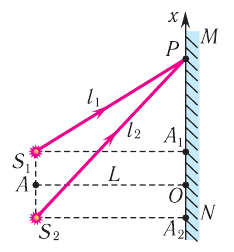
Рис. 60.

Решение

До некоторой точки 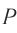 на экране каждая из волн проходит различные пут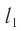и и 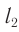. Максимумы и минимумы будут наблюдаться при выполнении условий:

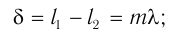
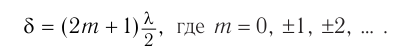
Из треугольников 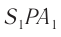и 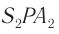по теореме Пифагора находим:

где 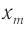— координата точки .

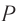Отсюда, вычитая из соотношения (2) соотношение (1), получаем:

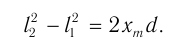
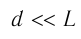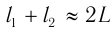С учетом того, что и , находим:

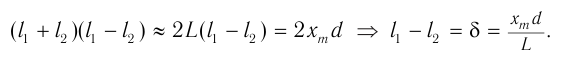
Из условия максимумов следует:

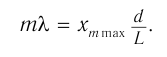
Тогда расстояние от центра экрана до 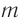-й светлой полосы находится из соотношения:

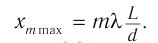
Из условия для минимумов находим положение темных полос:

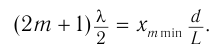
Отсюда

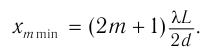
Расстояние между соседними максимумами:

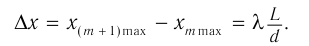
Из полученной формулы видно, что ширина интерференционных полос увеличивается при уменьшении расстояния 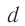 между когерентными источниками.

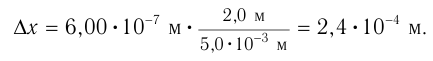
Ответ: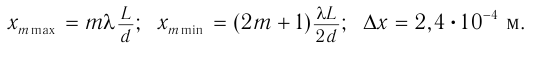

Принцип Гюйгенса — Френеля. Дифракция света. Дифракционная решетка

Среда называется однородной, если ее физические свойства по всему объему одинаковы во всех точках пространства. Среда называется изотропной, если ее физические свойства одинаковы по всем направлениям в пространстве.

Волновой фронт — это поверхность, все точки которой колеблются в одинаковых фазах, т. е. это поверхность равных фаз.

Волна называется плоской, если ее волновой фронт является плоскостью.

Закономерности распространения волн любой природы в различных средах носят универсальный характер.

Для наглядности рассмотрим процесс распространения волн на поверхности воды. Волны, возбуждаемые точечным источником 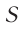, распространяются по всем направлениям с одинаковой по модулю скоростью 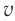. Следовательно, фронт волны будет иметь вид окружности (рис. 62). Соответственно, если волна будет распространяться в однородной изотропной среде по всем направлениям в пространстве, то ее волновой фронт будет иметь вид сферической поверхности. Как видно из рисунка 62, если в некоторый момент времени 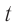фронт волны занимал положение I, то через промежуток времени 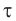фронт займет положение II, точки которого будут удалены от начального фронта волны на расстояние .

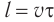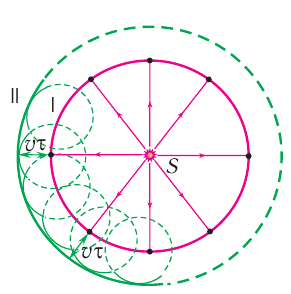
Рис. 62. Перемещение фронта волны по принципу Гюйгенса

Общие закономерности процесса распространения волн объяснил Христиан Гюйгенс, сформулировав в 1690 г. в «Трактате о свете» принцип, позволяющий определять положение волнового фронта через небольшой промежуток времени, зная его положение в данный момент времени. Согласно принципу Гюйгенса:

каждая точка среды, которой волновой фронт достиг в момент времени 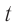, становится источником вторичных сферических волн. Новое положение волнового фронта через малый промежуток времени 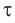определяется огибающей волновых фронтов вторичных волн в момент времени .

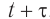Таким образом, согласно принципу Гюйгенса для нахождения положения волнового фронта через промежуток времени 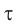проведем окружности радиусом 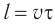, представляющие собой фронты вторичных волн с центрами на фронте в положении I (см. рис. 62). Соответственно, огибающая волновых фронтов вторичных волн определяет новое положение волнового фронта — положение II. Напомним, что огибающей называется поверхность, касательная ко всем вторичным волнам. На очень больших расстояниях от точечного источника излучаемые им волны можно считать плоскими.

Линия, перпендикулярная волновому фронту в данной точке, называется лучом. Луч определяет направление распространения волны, а также направление переноса энергии волной. Например, в солнечном излучении, приходящем на Землю, световые лучи являются практически параллельными друг другу.

Принцип Гюйгенса объясняет прямолинейное распространение волн в однородной среде. Поскольку в такой среде радиусы фронтов вторичных волн 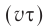одинаковы на всех участках (рис. 63), то волновой фронт 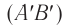плоской волны с течением времени перемещается в одном и том же направлении, оставаясь параллельным своему начальному положению .

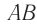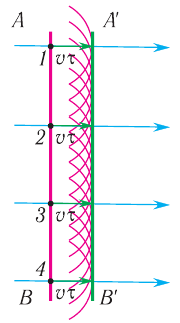
Рис. 63. Прямолинейное распространение волн (формирование фронта плоской волны)

Однако от закона прямолинейного распространения света наблюдаются отклонения при его распространении вблизи границ непрозрачных тел или прохождении через отверстия в непрозрачных экранах, т. е. в средах с резко выраженными неоднородностями. Причем отклонение существенно зависит от соотношения между длиной волны и размером препятствия. Действительно, стоя за углом дома, мы хорошо слышим, что едет автомобиль, хотя не видим его, поскольку находимся в области «тени». Таким образом, звуковые волны как бы «заворачивают за угол», в то время как световым волнам этого сделать не удается.

Явление огибания волнами препятствий, которое проявляется в отклонении направления распространения волн от прямолинейного, называется дифракцией (рис. 64). Явление дифракции служит одним из подтверждений волновой природы света.

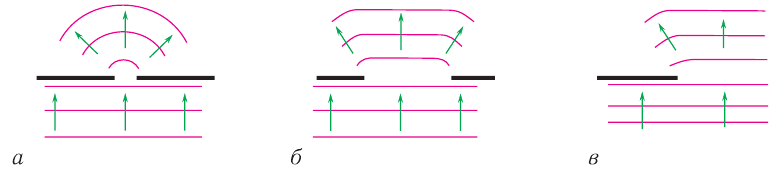
Рис. 64. Дифракция волн на различных препятствиях

Для проявления дифракции размеры препятствий (отверстий) должны быть меньше или сравнимы с длиной волны, вот почему в рассмотренном примере звук 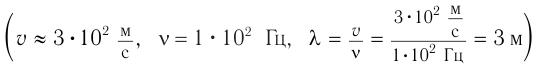мотора автомобиля смог «завернуть за угол», а свет 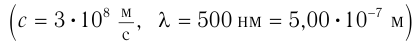, отраженный от автомобиля, — нет.

Принцип Гюйгенса позволяет решать задачи лишь о направлении распространения волнового фронта и не затрагивает вопрос об амплитуде, а следовательно, и об интенсивности распространяющихся по разным направлениям волн.

Изучая дифракцию света, французский физик Огюстен Жан Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн, которые являются когерентными. Принцип Гюйгенса — Френеля позволил описать явление дифракции количественно:

все источники вторичных волн, расположенные на волновом фронте, когерентны между собой. Для расчета амплитуды огибающей волны в данной точке пространства следует учесть интерференцию вторичных волн от всех участков волнового фронта в начальном положении.

Таким образом, согласно Френелю дифракция света объясняется интерференцией вторичных волн от различных участков начального положения волнового фронта.

Для наблюдения дифракции света используется дифракционная решетка.

Дифракционной решеткой называют оптический прибор, предназначенный для точного измерения длин волн и анализа состава света.

Дифракционная решетка состоит из большого числа равноотстоящих параллельных штрихов (щелей), нанесенных на стеклянную или металлическую поверхность. Длина решеток составляет 10—15 см. Они содержат 10 000—20 000 штрихов на 1 см. Наблюдения проводятся как в отраженном свете (на металлических решетках), так и в проходящем свете (на стеклянных).

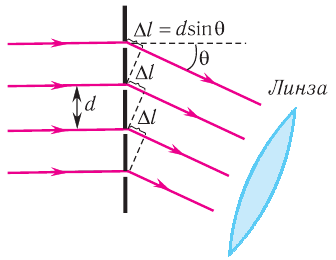
Рис. 65. Условие образования главных максимумов на дифракционной решетке

Рассмотрим дифракционную решетку, представляющую собой систему из 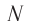одинаковых равноотстоящих параллельных щелей (прозрачные участки)в плоском непрозрачном экране (рис. 65). Если ширина каждой щели 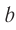, ширина непрозрачной части между щелями 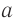, то величина 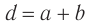называется постоянной решетки или ее периодом.

Пусть на решетку, постоянная которой равна 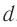, падает плоская волна, длина которой 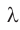. Из принципа Гюйгенса следует, что волны, дифрагировавшие на щелях, распространяются за решеткой по всем направлениям (рис. 66).

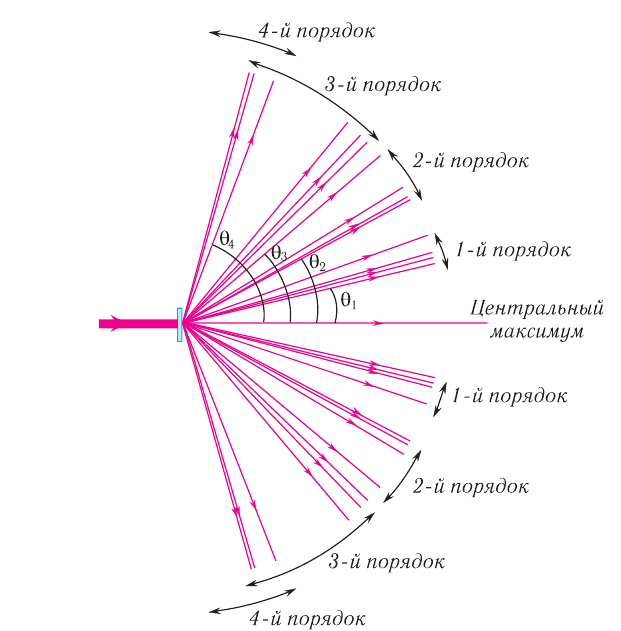
Рис. 66. Дифракционные спектры, полученные с помощью решетки, содержащей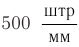 

Для наблюдения дифракционной картины на экране между ним и решеткой размещают собирающую линзу таким образом, чтобы экран находился в фокальной плоскости линзы (см. рис. 65). Собирающая линза фокусирует на экране падающие на нее параллельные лучи (вторичные волны).

В зависимости от разности хода между вторичными волнами, испущенными разными щелями, они интерферируют друг с другом, усиливая или ослабляя друг друга. На экране получается дифракционная картина в виде системы светлых и темных полос.

Наиболее яркие дифракционные максимумы получили название главных дифракционных максимумов.

Условие возникновения главных дифракционных максимумов, наблюдаемых под углами 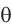, имеет вид:

Здесь 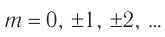— порядок максимума, или порядок спектра, 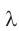— длина волны падающего излучения.

Полученное условие определяет направления распространения света в пространстве, по которым на отрезке 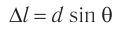укладывается целое число длин волн 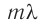(см. рис. 65).

Следовательно, вторичные волны от всех щелей решетки приходят в точку наблюдения синфазно (с фазами, отличающимися на число, кратное 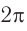) и усиливают друг друга.

Между максимумами интенсивности расположены минимумы, так как при изменении угла 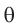на отрезке  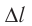уже не будет укладываться целое число длин волн.

Следовательно, вторичные волны приходят в точку наблюдения, ослабляя результирующее действие.

Из условия возникновения главных дифракционных максимумов (1) следует, что при 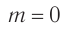для любых длин волн 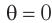. Следовательно, прямо по центру решетки образуется нулевой максимум, который называется также центральным максимумом. Дифракционные максимумы, соответствующие 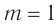, образуют спектр первого порядка, 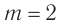— спектр второго порядка и т. д. (см. рис. 66).

Количество максимумов т в дифракционной картине ограничено, поскольку 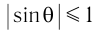. Максимальный порядок спектра 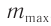, который дает дифракционная решетка при нормальном падении света на нее, определяется из условия .

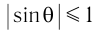Рис. 67. Дифракционный спектр белого света (а); дифракционные максимумы красного света (б); дифракционные максимумы синего света (в).

Тогда из соотношения (1) следует:

т. е. зависит от периода решетки и длины световой волны.

Таким образом, для получения спектра первого порядка 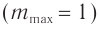необходимо, как следует из соотношения (2), чтобы период решетки был больше длины световой волны .

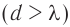При падении на решетку белого света центральный максимум 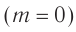представляет собой изображение источника (рис. 67, а), так как в этом направлении собирается излучение всех длин волн. Для всех максимумов ненулевого порядка 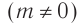в дифракционной решетке 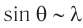. Следовательно, красные лучи, имеющие большую длину волны, чем синие, отклоняются дифракционной решеткой сильнее (рис. 67, б, в).

Таким образом, при освещении решетки белым светом справа и слева от центрального максимума наблюдаются максимумы первого, второго и более высоких порядков, обращенных фиолетовым краем к центру дифракционной картины, а красным от нее (см. рис. 67, а).

С увеличением числа щелей в дифракционной решетке возрастает количество световой энергии, пропускаемой решеткой, следовательно, интенсивность главных максимумов при этом увеличивается.

Кроме того, главные максимумы из расплывчатых превращаются в резкие и узкие, которые разделены практически темными промежутками, так как вторичные максимумы очень слабы и составляют не более 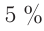от главного (рис. 68). Отношение интенсивностей максимумов в нулевом, первом и втором порядках: 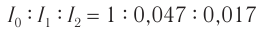. Поэтому при падении монохроматического излучения на решетки, в которых число штрихов на 1 см достигает 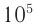, дифракционный спектр состоит из очень резких линий.

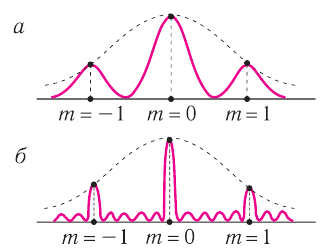
Рис. 68. Изменение дифракционной картины при увеличении числа щелей: а — две щели; б — шесть щелей

Первая дифракционная решетка, сконструированная американским ученым Риттенхаузом, состояла из параллельного ряда волосков диаметром около 0,1 мм и длиной 10 мм, натянутых на расстоянии порядка 0,2 мм один от другого. Немецкий физик Йозеф Фраунгофер вместо волосков использовал штрихи, наносимые на стекло алмазным острием. Их число на 1 мм решетки достигало у него 300.

Пример №2

На дифракционную решетку, имеющую , падает монохроматическое излучение длиной волны 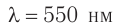. Определите наибольший порядок 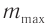дифракционного максимума, который можно наблюдать при нормальном падении излучения на решетку.

Решение

Условие дифракционных максимумов:

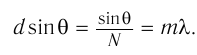
Следовательно,

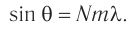
Наибольший порядок 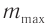дифракционного максимума наблюдается при угле 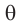, близком к углу 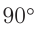. Вследствие этого будем считать, что

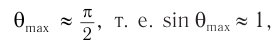
тогда наибольший порядок максимума находится по формуле:

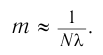
Для определения 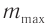необходимо взять целую часть полученного значения:

Ответ: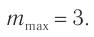

Закон преломления света. Показатель преломления. Полное отражение

Изменение направления распространения луча света при прохождении через границу раздела двух сред называется преломлением света.

Геометрической оптикой называют раздел оптики, в котором изучаются законы распространения оптического излучения на основе представления о световых лучах.

Под лучом понимают линию, вдоль которой переносится энергия электромагнитной волны. Условимся изображать световые лучи графически с помощью геометрических линий со стрелками. В геометрической оптике волновая природа

света не учитывается.

Геометрическому лучу на практике соответствует тонкий световой пучок, получаемый при пропускании светового излучения, идущего от удаленного источника, через отверстие (диафрагму) в экране (рис. 69).

Рис. 69. Световой пучок

Таким образом, следует различать геометрический луч (математическое понятие) и световой пучок (материальный объект), получаемый от источника света.

Уже в начальные периоды оптических исследований были экспериментально установлены четыре основных закона геометрической оптики:

• закон прямолинейного распространения света;
• закон независимости световых лучей;
• закон отражения световых лучей;
• закон преломления световых лучей.

Световой поток можно разделить на отдельные световые пучки, выделяя их при помощи диафрагм. Действие выделенных световых пучков оказывается независимым друг от друга, т. е. эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно с ним другие пучки или нет.

Световые пучки получают при пропускании светового излучения, идущего от удаленного источника, через отверстие (диафрагму) в экране 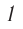 (рис. 70). Для того чтобы можно было пренебречь дифракционным расширением пучка, должно выполняться условие:

где 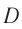 — размер препятствия или отверстия, на котором свет дифрагирует, 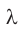— длина световой волны, 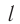— расстояние от препятствия до места наблюдения дифракционной картины.

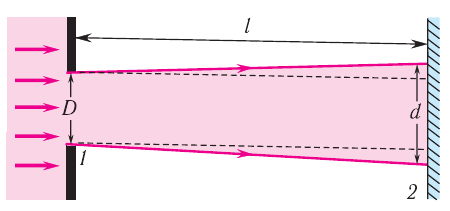
Рис. 70. Распространение света через щель

В этом случае выходящий из диафрагмы пучок будет оставаться неизменным, и он называется параллельным.

Соотношение (1) выполняется, когда длина световой волны стремиться к нулю 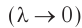. Поэтому геометрическая оптика является предельным приближенным случаем волновой оптики.

Если диаметр диафрагмы или размеры предмета оказываются сравнимы с длиной световой волны 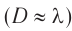, то выходящий световой пучок становится расходящимся, свет проникает в область геометрической тени, происходит дифракция света, т. е. проявляется волновой характер светового излучения.

Лучи, выходящие из одной точки, называют расходящимися, а собирающиеся в одной точке — сходящимися. Примером расходящихся лучей может служить наблюдаемый свет далеких звезд, а примером сходящихся — совокупность лучей, попадающих в зрачок нашего глаза от различных предметов.

Для изучения свойств световых волн необходимо знать закономерности их распространения в однородной среде, а также закономерности отражения и преломления на границе раздела двух сред.

Рассмотрим падение плоской световой волны на плоскую поверхность раздела однородных изотропных и прозрачных сред при условии, что размеры поверхности раздела намного больше длины волны падающего излучения.

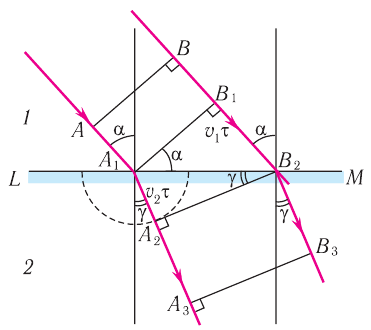
Рис. 71. Преломление света в соответствии с принципом Гюйгенса: 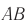— фронт падающей плоской волны; 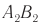— фронт волны после преломления

Пусть на плоскую поверхность раздела 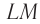двух сред падает плоская световая волна, фронт которой 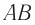(рис. 71). Если угол падения 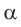отличен от нуля, то различные точки фронта 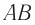волны достигнут границы раздела 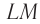не одновременно.

Рассмотрим, что будет происходить во второй среде, считая, что модуль скорости 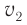распространения света в ней меньше, чем в первой 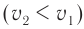(см. рис. 71).

Фронт падающей волны 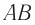будет перемещаться со скоростью, модуль которой 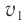по направлению 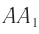. К моменту времени (за промежуток времени 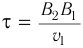), когда точка 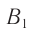фронта достигнет границы раздела двух сред (точка 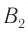), вторичная волна из точки 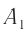(согласно принципу Гюйгенса) пройдет расстояние 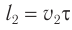. Фронт волны, распространяющейся во второй среде, можно получить, проводя прямую линию, касательную к полуокружности с центром в точке .

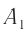Из построения видно, что 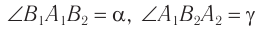как углы с взаимно перпендикулярными сторонами. Из 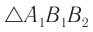находим: 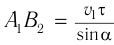и из — .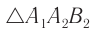

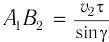Отсюда: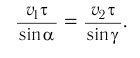  

Из этого выражения следует закон преломления:

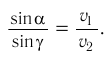
Напомним, что абсолютным показателем преломления называется отношение модуля скорости распространения световой волны в вакууме 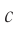 к модулю скорости распространения в данной среде.

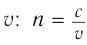С учетом этого соотношения закон преломления принимает вид:

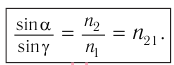
Величина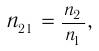 

равная отношению абсолютных показателей преломления 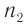второй и 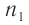первой сред, называется относительным показателем преломления второй среды относительно первой. В отличие от абсолютного показателя преломления относительный показатель преломления может быть и меньше единицы, если .

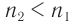Таким образом, исходя из волновой теории света, получен закон преломления световых волн:

отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух данных сред и равная относительному показателю преломления второй среды относительно первой;

лучи, падающий и преломленный, лежат в одной плоскости с перпендикуляром, проведенным в точке падения луча к плоскости границы раздела двух сред.

Перепишем закон преломления в следующем виде:

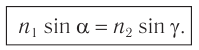
При такой записи закона преломления не надо запоминать абсолютный показатель преломления какой среды стоит в числителе, а какой — в знаменателе.

Необходимо всегда умножать абсолютный показатель преломления на синус угла, относящийся к одной и той же среде.

Для наблюдения явления преломления света достаточно поместить карандаш в стакан с водой и посмотреть на него со стороны — карандаш будет казаться «надломленным» (преломленным) (рис. 72), оставаясь при этом совершенно целым.

Рис. 72. Преломление света на границе раздела двух сред

Первые упоминания о преломлении света в воде и стекле встречаются в труде Клавдия Птолемея «Оптика», вышедшем в свет во II в. н. э.

Закон преломления света был экспериментально установлен в 1620 г. голландским ученым Виллебродом Снеллиусом. Заметим, что независимо от Снеллиуса закон преломления был также открыт Рене Декартом.

Причиной преломления волн, т. е. изменения направления распространения волн на границе раздела двух сред, является изменение модуля скорости распространения электромагнитных волн при переходе излучения из одной среды в другую.

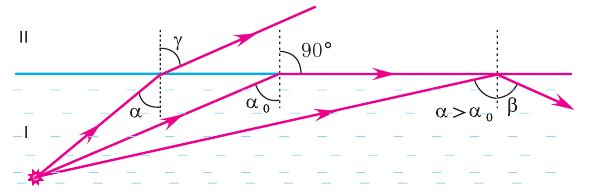
Рис. 73. Полное отражение света на границе раздела сред

Как следует из закона преломления, при переходе света из оптически более плотной среды I (с большим абсолютным показателем преломления 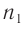) в оптически менее плотную среду  II (с меньшим показателем преломления 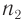) угол преломления 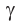становится больше угла падения 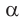(рис. 73).

По мере увеличения угла падения, при некотором его значении 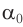, угол преломления станет 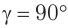, т. е. свет не будет попадать во вторую среду. Энергия преломленной волны при этом станет равной нулю, а энергия отраженного излучения будет равна энергии падающего. Следовательно, начиная с этого угла падения, вся световая энергия полностью отражается от границы раздела этих сред в среду I.

Это явление называется полным отражением света (см. рис. 73). Угол 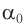, при котором возникает полное отражение, называется предельным углом полного отражения. Он определяется из закона преломления при условии, что угол преломления :

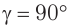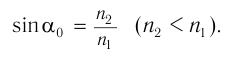
Таким образом, преломленная волна отсутствует при углах падения, больших предельного угла 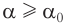. Например, для границы вода 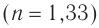— воздух предельный угол полного отражения 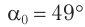, для границы алмаз 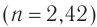— воздух — .

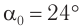Явление полного отражения используют в волоконной оптике для передачи света и изображения по пучкам прозрачных гибких световодов (рис. 74), а также в отражательных призмах различных оптических приборов. В волоконно-оптических устройствах, в которых свет распространяется по тонким световодам, стеклянная световедущая жила покрыта слоем вещества с меньшим показателем преломления.

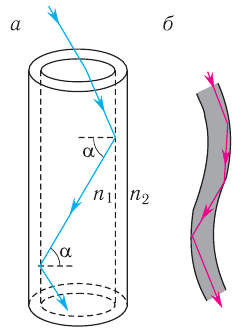
Рис. 74. Ход лучей в световоде: а — прямом; б — гибком

В 2009 г. китайский ученый Чарльз Пао удостоен Нобелевской премии за выдающийся вклад в исследование световодов для оптической связи. В 1954 г. белорусским физиком, академиком Федором Ивановичем Федоровым было теоретически предсказано новое физическое явление — поперечное смещение (перпендикулярно плоскости падения) светового пучка при его полном отражении. Это смещение меньше длины волны, и для его наблюдения световой пучок должен быть ограниченным в поперечном направлении. В 1969 г. французским физиком К. Эмбером оно было подтверждено экспериментально и получило название «сдвиг Федорова».

• Заказать решение задач по физике

Пример №3

Определите угол падения 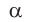луча на стеклянную пластинку с показателем преломления 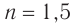, если между отраженным и преломленным лучами угол .

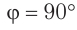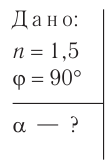
Решение

Из закона преломления находим:

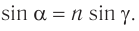
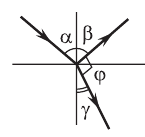
Рис. 75

Из геометрического построения (рис. 75) следует, что углы отражения и преломления связаны соотношением: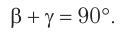  

Отсюда 

Подставляем найденный угол 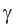в формулу закона преломления и с учетом закона отражения  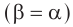определяем искомый угол падения:

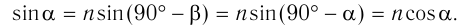
Отсюда

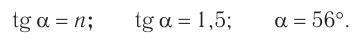
Ответ: .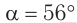

Прохождение света через плоскопараллельные пластинки и призмы

Законы отражения и преломления света широко используются для управления ходом световых пучков. Для отражения света в приборах применяются зеркала и призмы, для преломления — призмы, плоскопараллельные пластинки, линзы.

Зеркала, призмы, пластинки и линзы являются элементами, комбинируя которые, создают различные оптические приборы. Рассмотрим отдельные элементы оптических приборов.

Плоскопараллельная пластинка. Рассмотрим ход луча в плоскопараллельной пластинке. На рисунке 77 показан ход светового луча в плоскопараллельной пластинке толщиной 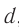, находящейся в воздухе.

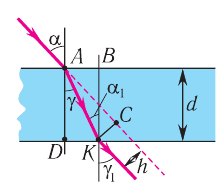
Рис. 77. Ход луча в плоскопараллельной пластинке

Согласно закону преломления на первой и второй границах раздела для луча, падающего под углом 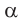на первую границу, имеем:

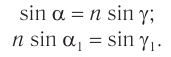
Здесь 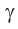 — угол преломления на первой границе, 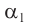— угол падения луча на вторую границу, 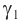— угол преломления на второй границе, 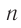— абсолютный показатель преломления вещества пластинки.

Накрест лежащие углы 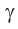и 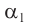при параллельных прямых 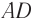и 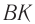(перпендикулярах к первой и второй параллельным границам) равны, т. е. 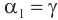. Следовательно, 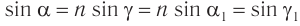. Откуда следует, что

Таким образом, луч света, проходя через плоскопараллельную пластинку, с обеих сторон которой находится одна и та же среда, смещается параллельно своему начальному направлению на некоторое расстояние .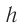

Соответственно, все предметы, если смотреть на них сквозь прозрачную плоскопараллельную пластинку под углом, не равным нулю, будут также казаться смещенными.

Найдем, от каких параметров пластинки зависит смещение 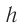луча. Из 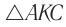следует, что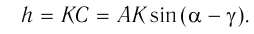 

Из 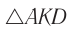имеем:

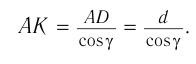
Отсюда: 

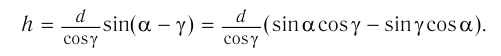
С учетом закона преломления 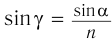  и тригонометрического тождества  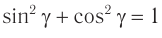находим:

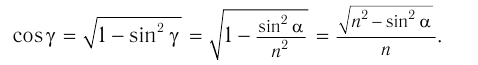
Расстояние 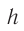 между направлениями входящего и выходящего лучей можно определить из соотношения

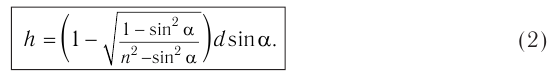
Как видно из соотношения (2), смещение 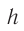луча при данном угле падения 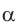зависит от толщины  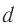пластинки и ее показателя преломления  .

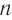Трехгранная призма

Рассмотрим ход луча в трехгранной призме. Пусть световой луч 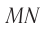 падает под углом 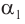на боковую грань трехгранной призмы 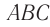, сечение которой показано на рисунке 78. Призма, изготовленная из вещества с абсолютным показателем преломления 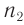, находится в среде с абсолютным показателем преломления 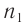. Угол 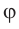при вершине 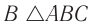называется преломляющим углом призмы. Грани призмы, образующие преломляющий угол 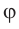, называются преломляющими. Грань, лежащая напротив преломляющего угла, называется основанием призмы.

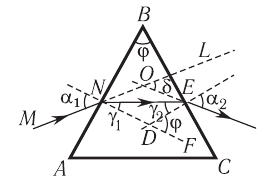
Рис. 78. Ход луча в призме

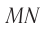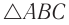Пусть луч и лежат в одной плоскости — плоскости листа книги. Из закона преломления света находим угол преломления :

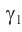Если показатель призмы 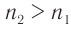, то преломленный луч 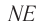падает на вторую боковую грань призмы под углом 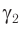. Полного отражения на второй преломляющей грани не происходит при условии 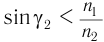, и луч выходит из призмы под углом 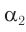. Его находим из закона преломления:

Отклонение от начального направления луча 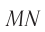вследствие преломлений на гранях призмы определяется углом 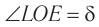(см. рис. 78). Угол 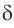между направлениями входящего и выходящего лучей называется углом отклонения. Рассмотрим 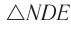. С учетом того, что 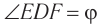, по теореме о внешнем угле треугольника находим:

Применим эту же теорему к :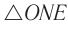

Из формул (5) и (6) определим связь угла падения 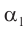, угла преломления 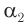с преломляющим углом 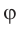призмы и углом отклонения 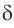выходящего луча от начального направления:

В результате получим систему уравнений (3), (4), (5), (7):

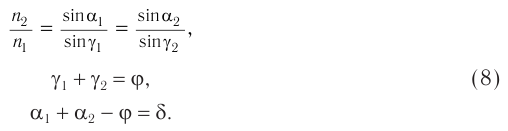
Система уравнений (8) позволяет решить задачу на прохождение луча света через трехгранную призму без полного отражения на ее гранях.

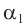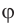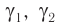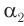Если угол падения на грань призмы и преломляющий угол призмы малы, то малыми будут и углы и . Поэтому в законах преломления (3) и (4) отношение синусов можно заменить отношением углов, выраженных в радианах, т. е.:

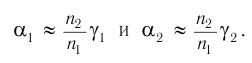
Подставляя полученные выражения для 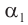и 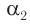 в соотношение (7), находим:

Из соотношения (9) следует, что, во-первых: чем больше преломляющий угол 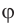, тем больше угол отклонения 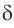лучей призмой; во-вторых, угол отклонения 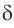лучей увеличивается с ростом абсолютного показателя преломления  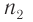вещества призмы. Как видно из рисунка 78, луч света, проходя через трехгранную призму, отклоняется к ее утолщенной части, если абсолютный показатель преломления вещества призмы больше абсолютного показателя преломления окружающей среды .

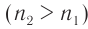Пример №4

Определите наименьший преломляющий угол стеклянной призмы, находящейся в воздухе, при котором луч, падающий нормально на грань призмы, не выйдет через ее вторую боковую грань (рис. 79). Показатель преломления стекла призмы .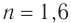

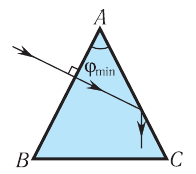
Рис. 79

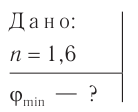
Решение

Запишем условие полного отражения на боковой грани :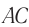

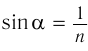
Вследствие того, что 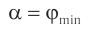как углы с взаимно перпендикулярными сторонами:

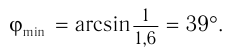
Ответ: .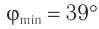

Формула тонкой линзы

Линза называется собирающей, если после преломления в ней параллельный пучок становится сходящимся. Если же после преломления в линзе параллельный пучок становится расходящимся, то линза называется рассеивающей (рис. 80).

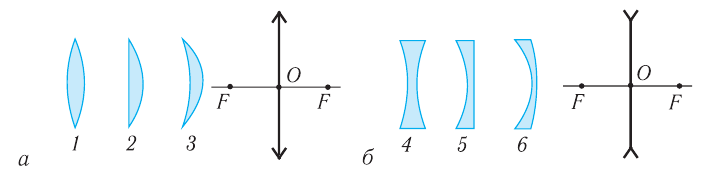
Рис. 80. Типы линз и их условные обозначения: а — собирающие: / — двояковыпуклая; 2 — плосковыпуклая; 3 — выпукло-вогнутая; б — рассеивающие: 4 — двояковогнутая; 5 — плосковогнутая; б — вогнуто-выпуклая

Величина, обратная фокусному расстоянию линзы, выраженному в метрах, называется ее оптической силой:

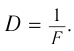
Единица оптической силы — 1 диоптрия ().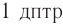

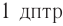соответствует оптической силе линзы с фокусным расстоянием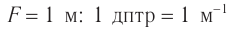 

Линзы можно представить в виде совокупности частей трехгранных призм. На рисунке 81, а изображена модель двояковыпуклой линзы, собранной из частей призм, повернутых основаниями к центру линзы. Соответственно, модель двояковогнутой линзы будет представлена частями призм, повернутых основаниями от центра линзы (рис. 81, б).

Преломляющие углы этих призм можно подобрать таким образом, чтобы падающие на нее параллельные лучи после преломления в призмах собрались в одной точке .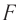

Линза считается тонкой, если ее толщина в центре намного меньше радиусов ограничивающих ее поверхностей. Тонкая линза дает неискаженное изображение только в том случае, если свет монохроматический и предмет достаточно мал, следовательно, лучи распространяются вблизи главной оптической оси. Такие лучи получили название параксиальных.

Отметим условия, при одновременном выполнении которых линза является собирающей:

толщина в центре больше толщины у краев;

ее показатель преломления больше показателя преломления окружающей среды.

При невыполнении (или выполнении) только одного из этих условий линза является рассеивающей.

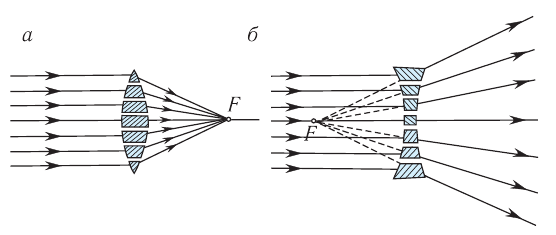
Рис. 81. Модель линзы: а — двояковыпуклой; б — двояковогнутой

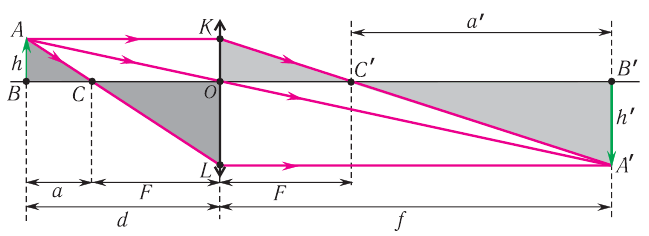
Рис. 82. Построение изображения предмета в тонкой собирающей линзе

Между фокусным расстоянием тонкой линзы, расстоянием от предмета до линзы и от линзы до изображения существует определенная количественная зависимость, называемая формулой линзы.

Выведем формулу тонкой линзы из геометрических соображений, рассматривая ход характерных лучей. Обратим внимание на луч, идущий через оптический центр 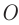линзы, луч, параллельный главной оптической оси линзы, и луч, проходящий через главный фокус линзы.

Построим изображение предмета 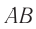 в тонкой собирающей линзе (рис. 82). Пусть расстояние от предмета до линзы 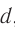, расстояние от линзы до изображения 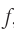, фокусное расстояние линзы 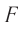, расстояние от предмета до переднего главного фокуса 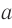, расстояние от заднего главного фокуса до изображения 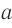, высота предмета 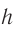, высота его изображения .

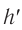Из рисунка 82 видно, что 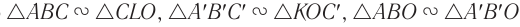. Из подобия треугольников следует:

Используя соотношения (1) и (2), получим:

Соотношение 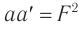называется формулой Ньютона.

С учетом того, что 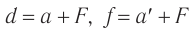(см. рис. 82), находим: 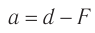и 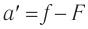и подставляем в формулу (4):

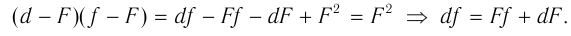
Разделив обе части последнего выражения на 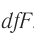, получаем формулу тонкой линзы:

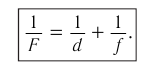
Линейным (поперечным) увеличением 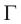называется отношение линейного размера изображения 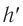к линейному размеру предмета 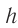. Из соотношения (3) находим линейное увеличение тонкой линзы:

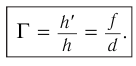
В 1604 г. в исследовании «Дополнения к Вителло» И. Кеплер изучал преломление света в линзах различной конфигурации и для малых углов падения пришел к формуле линзы.

Для практического использования формулы линзы следует твердо запомнить правило знаков:

для собирающей линзы, действительного источника и действительного изображения величины 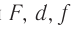 считают положительными. Для рассеивающей линзы, мнимого источника и мнимого изображения величины 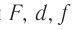считают отрицательными.

Заметим, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей.

Таким образом, линза с 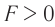является собирающей (положительной), а с 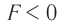— рассеивающей (отрицательной).

Оптическая сила линзы зависит от свойств окружающей среды (вспомните, как плохо мы видим под водой без плавательных очков).

В современных оптических приборах для улучшения качества изображений используются системы линз. Оптическая сила 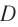системы тонких линз, сложенных вместе, равна сумме их оптических сил :

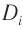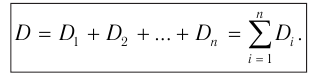
Пример №5

На каком расстоянии 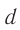от рассеивающей линзы с оптической силой 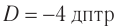надо поместить предмет, чтобы его мнимое изображение получилось в 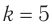раз меньше 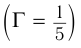самого предмета? Постройте изображение предмета.

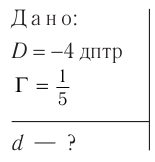
Решение

Из формулы для линейного увеличения

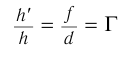
находим:

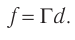
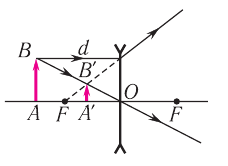
Рис. 83

По формуле тонкой линзы (рис. 83) с учетом правила знаков:

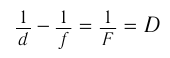
и с учетом выражения для 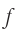 получаем:

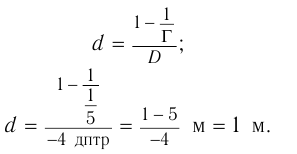
Ответ: .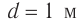

Оптические приборы для получения действительных изображений

Посредством глаза, а не глазом Смотреть на мир умеет разум.

Вильям Блейк

Познакомимся с оптическими приборами, широко используемыми человеком.

По своему назначению оптические приборы подразделяются на две большие группы:

1. для получения действительных изображений предметов (проекционные, фотоаппараты);
2. для увеличения угла зрения (лупа, микроскоп, подзорная труба).

В данном параграфе рассмотрим приборы для получения действительных изображений предметов.

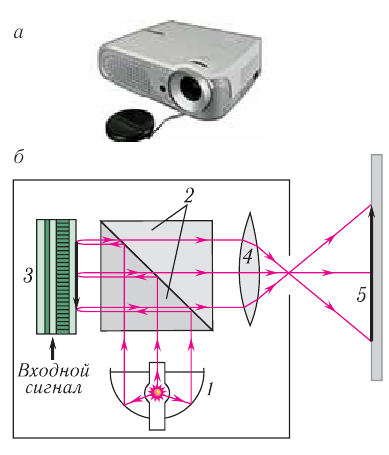
Рис. 87. Мультимедийный проектор, работающий по технологии отражения: а — общий вид; б — оптическая схема

Мультимедийный проектор — оптический прибор, используя который на экране получают действительное (прямое или обратное) увеличенное изображение, «снятое» с экрана компьютера, телевизора или других источников видеосигнала (рис. 87, а).

Для формирования изображения в мультимедийных проекторах используются различные базовые технологии: жидкокристаллическая технология, технология цифровой обработки света или технология формирования цифровых изображений методом отражения. При формировании цифрового изображения методом отражения источник света 1 при помощи разделяющих призм 2 освещает оптическую матрицу с изображением 3 и при помощи системы проекционных линз 4 передает изображение на экран 5 (рис. 87, б).

Популярность мультимедийных проекторов обусловлена их универсальностью, поскольку помимо компьютерного изображения они поддерживают практически все существующие стандарты видеозаписей, а также полностью совместимы с активно развивающимся телевидением высокой четкости.

Проекторы активно используются на научных конференциях, выставках, семинарах и т. д., поскольку по размерам изображения и по возможностям его настройки с ними не способны конкурировать ни жидкокристаллические телевизоры, ни плазменные.

Фотоаппарат — прибор, предназначенный для получения действительных уменьшенных обратных изображений предметов на фотопленке. При этом предметы могут быть расположены на различном удалении от точки съемки. Фотоаппарат состоит из закрытой светонепроницаемой камеры и системы линз, называемых объективом  (рис. 88).

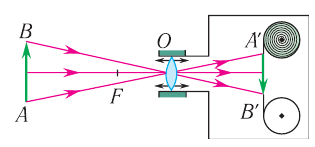
Рис. 88. Ход лучей в фотоаппарате: 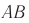 — предмет; 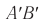— изображение на фотопленке; 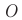— объектив

Перемещая объектив фотоаппарата, добиваются наводки на резкость, при которой изображение предмета формируется точно на фотопленке. В противном случае изображение получается нечетким (размытым). Количество световой энергии, поступающей на пленку, определяется размерами диафрагмы и временем открытия затвора (выдержкой).

Фотографический метод регистрации изображения изобрели в 1839 г. Л. Дагер и Ж. Ньепс.

Рис. 89. Цифровой фотоаппарат

На смену пленочным пришли электронные (цифровые) фотокамеры (рис. 89), в которых изображение записывается не на фотопленку, а на специальный чувствительный элемент. Он покрыт сенсорами освещенности, каждый из которых имеет фильтр одного из основных цветов: синий, красный или зеленый.

На элементе формируется точка изображения — пиксель (от англ. pixel (picture element) — элемент изображения). Чем больше пикселей, тем более качественное изображение получается. Поэтому важнейшей характеристикой цифрового фотоаппарата является его разрешение, т. е. количество пикселей. У самых простых фотоаппаратов оно составляет несколько мегапикселей, а у лучших — до нескольких десятков мегапикселей.

Количество сенсоров влияет также на величину изображения, которую можно получить с помощью данного аппарата.

При нажатии кнопки затвора на каждом пикселе чувствительного элемента аппарата фиксируется интенсивность каждого из трех цветов. Процессор аппарата, как у компьютера, собирает информацию о цвете в файл и записывает его на запоминающее устройство — карту памяти. После этого ее можно просматривать на компьютере или специальной приставке. Но самое важное, и на самом фотоаппарате можно сразу посмотреть сделанный снимок, что является огромным преимуществом цифрового фотоаппарата.

Какие еще достоинства имеет цифровой фотоаппарат?

Во-первых, возможность получения неограниченно большого количества копий без потери качества «оригинала» фотографии.

Во-вторых, возможность использования фотоаппарата при различных световых условиях и с разных расстояний (например, у некоторых моделей от 2 см) без дополнительных устройств.

В-третьих, возможность использования цифровых изображений для переноса на различные поверхности и размещения на Web-сайте, а также редактирования с помощью различных компьютерных программ.

В-четвертых, возможность сделать большое количество снимков с минимальным интервалом времени (10 и более кадров в секунду).

В-пятых, габаритные размеры и масса. Например, некоторые аппараты имеют размеры 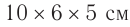и массу 200 г.

Оптические приборы для увеличения угла зрения

Основную часть информации (примерно 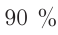) об окружающем мире мы получаем с помощью органов зрения.

Расстояние наилучшего зрения — это расстояние от предмета до глаза, при котором глазные мышцы не устают и угол зрения максимален.

Размер изображения 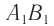 предмета 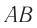на сетчатке (рис. 90) определяется углом зрения  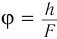,  вершина которого находится в оптическом центре глаза — точке .

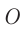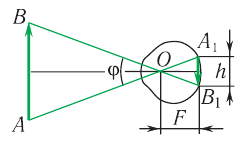
Рис. 90. Ход лучей в глазу

Угол зрения образован лучами, направленными на крайние точки предмета, т. е. это угол, под которым виден предмет из оптического центра глаза. Отметим, что изображение на сетчатке всегда действительное, уменьшенное и перевернутое.

От бесконечно удаленного предмета в глаз попадает пучок параллельных лучей. В этом случае 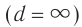 аккомодации не требуется. Если предмет приближается, то лучи становятся расходящимися. В этом случае оптическая система глаза собирает лучи на сетчатке. В отличие от фотоаппарата, наводка на резкость достигается не перемещением «объектива» хрусталика, а изменением его оптической силы.

Понятие нормальный глаз человека характеризуется расстоянием наилучшего зрения около 25 см и пределом зрения (дальняя точка), находящимся на бесконечности.

С возрастом возможность аккомодации быстро уменьшается в основном из-за уплотнения хрусталика, теряющего способность достаточно сжиматься. Пожилой человек не может отчетливо видеть близкие предметы, а также различать буквы в газетах и книгах. К пятидесяти годам расстояние наилучшего зрения увеличивается в среднем до 50 см.

С возрастом, вследствие болезни или при несоблюдении гигиены у глаз могут появиться дефекты. Два наиболее распространенных дефекта зрения — близорукость и дальнозоркость.

Очки — первый оптический прибор, примененный человеком. Появились они довольно давно — в XIII — XIV вв. Для исправления близорукости используют очки с рассеивающими линзами, а дальнозоркости — очки с собирающими линзами. Сейчас очки стали обычным предметом обихода и многим дают возможность нормально жить и работать. Другой разновидностью устройств, корректирующих зрение, являются контактные линзы. Помимо практичности, их особенностью является плотный контакт с роговицей, позволяющий значительно уменьшить искажения и увеличить поле зрения системы глаз-линза.

Наш глаз не дает возможности видеть очень малые объекты без специальных вспомогательных устройств, так как мы ясно видим объект только в том случае, когда воспринимаем зрительные впечатления от различных точек объекта.

Соответственно, две точки можно раздельно видеть только тогда, когда их изображения получаются на различных чувствительных элементах сетчатки — палочках или колбочках. Для этого необходимо, чтобы лучи от рассматриваемых точек шли через оптический центр глаза под углом около 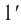. Поэтому для нормального глаза минимальный размер изображения составляет примерно 3,6 мкм. Кроме того, минимальный угол зрения должен соответствовать дифракционному расширению пучка, вызванному его прохождением через зрачок.

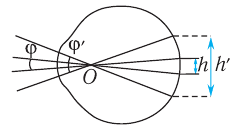
Рис. 91. Увеличение угла зрения

Чем больше угол 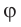  между прямыми, соединяющими оптический центр глаза  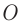(рис. 91) с крайними точками предмета (угол зрения), тем яснее виден предмет и тем большее число различных деталей можно различить. Угол зрения можно увеличить 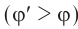, приближая предмет к глазу или глаз к предмету. При этом размер изображения на сетчатке также увеличивается .

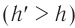Таким образом, увеличение объема зрительной информации может быть достигнуто лишь за счет увеличения угла зрения. Простейший способ увеличить угол зрения — приблизить предмет к глазу. Однако это не всегда возможно. Наименьшее расстояние до глаза, при котором мы еще видим предмет, определяется ближним пределом аккомодации. Опыт показывает, что объект не фокусируется на сетчатке, если он находится от глаза на расстоянии ближе 14 см. Вследствие этого возникает потребность в создании приборов, позволяющих увеличить угол зрения.

Оптические приборы, вооружающие глаз, подразделяются на две группы:

1. приборы для рассматривания очень мелких объектов (лупа, микроскоп), которые эти объекты как бы «увеличивают»;
2. приборы, предназначенные для рассматривания удаленных объектов (зрительные трубы, бинокли, телескопы), которые эти объекты как бы «приближают».

Лупа — оптический прибор (собирающая линза), позволяющий увеличить угол зрения (т. е. увеличить мелкие детали предметов) (рис. 92).

Лупа представляет собой короткофокусную линзу (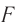 от 10 мм до 100 мм), которая располагается между глазом и предметом.

Мнимое увеличенное изображение предмета получается на расстоянии наилучшего зрения — 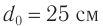для нормального глаза (рис. 93). Таким образом изображение предмета рассматривается глазом практически без напряжения.

Рис. 92. Лупа

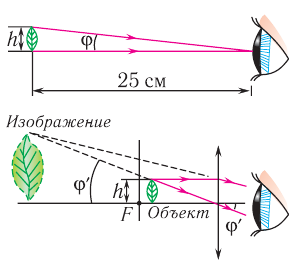
Рис. 93. Мелкий предмет, рассматриваемый: а — невооруженным глазом на расстоянии наилучшего зрения; б — через лупу

Видимое увеличение, которое дает лупа:

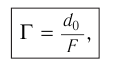
где 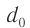— расстояние наилучшего зрения, 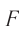— фокусное расстояние лупы.

Вследствие того, что 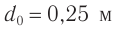, обычно лупы имеют увеличение от 2,5 до 25 раз. Лупы с увеличением 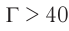не применяются из-за сильных искажений изображения или малости обзора.

В XVII в. голландский мастер Антони ван Левенгук с помощью линз мог видеть капилляры кровеносной системы, красные кровяные тельца, изучать подробности строения простейших одноклеточных.

Микроскоп (от греч. micros — малый и skopeo — смотрю) — оптический прибор для получения сильно увеличенных изображений объектов или деталей их структуры, не видимых невооруженным глазом.

Назначение микроскопа состоит в том, чтобы получать с его помощью такое изображение не различимого для глаза предмета, которое, не находясь ближе 14 см от глаза, рассматривалось бы под углом зрения большим, чем предельный угол в .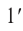

Микроскоп (рис. 94, а) состоит из двух собирающих линзовых систем: объектива 1 с фокусным расстоянием 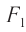, равным нескольким миллиметрам, и окуляра 2 с фокусным расстоянием 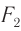, равным нескольким сантиметрам (рис. 94, б). Предмет 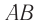помещается перед фокусом объектива. Расстояние между фокусами объектива и окуляра равно 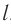, причем .

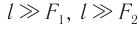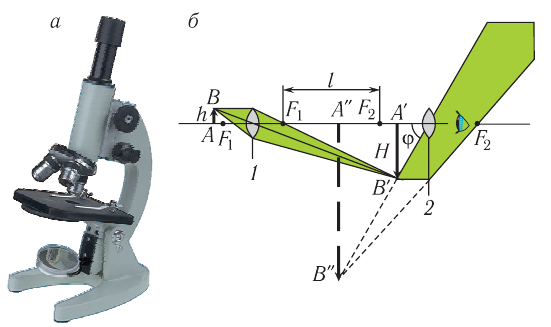
Рис. 94. Микроскоп: а — общий вид; б — оптическая схема и ход лучей

За объективом (за фокусом 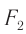) получается действительное увеличенное изображение 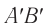предмета, которое является предметом наблюдения для окуляра. Окончательное изображение 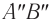предмета является мнимым, перевернутым и увеличенным (см. рис. 94, б). Увеличение  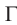микроскопа определяется увеличением объектива 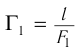и окуляра :

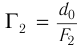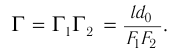
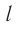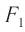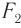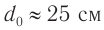Здесь — оптическая длина тубуса микроскопа, т. е. расстояние между фокальными точками , и ,   — расстояние наилучшего зрения для нормального глаза.

В микроскоп объект виден детальнее, поскольку рассмотрение мнимого изображения 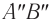объекта в окуляр осуществляется под большим углом зрения.

Из-за явления дифракции в микроскоп невозможно рассматривать объекты, размеры которых сравнимы с длиной волны света. Таким образом, максимальное увеличение микроскопа ограничено 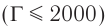вследствие волновой природы света.

В XVII в. появились первые микроскопы. Левенгук прославился своими микроскопами, которые давали увеличение до 270 раз.

При рассматривании крупных, но очень удаленных объектов угол зрения мал и может быть меньше предельного. В этом случае для увеличения угла зрения применяются бинокли и телескопы.

Телескопы — астрономические оптические приборы, предназначенные для наблюдения небесных тел. О них вам будет подробно рассказано в курсе астрономии.

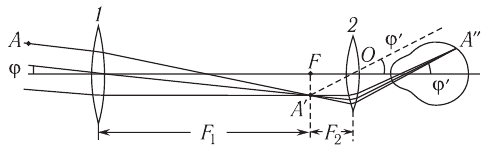
Рис. 95. Ход лучей в трубе Кеплера

Простейшим телескопом является подзорная труба. Она состоит из двух линзовых систем — объектива 1 и окуляра 2 (рис. 95). Подзорная труба с собирающим окуляром называется трубой Кеплера. Для получения максимального угла зрения в трубе Кеплера совмещают задний фокус объектива и передний фокус окуляра. В таком случае при рассматривании удаленного предмета из окуляра выходят пучки параллельных лучей. Это позволяет наблюдать удаленные объекты в телескоп нормальным глазом в ненапряженном состоянии (без аккомодации ).

Рассматриваемый предмет 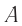обычно находится на очень большом расстоянии от объектива. Промежуточное изображение 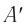получается практически сразу за фокусом объектива. Оно расположено от окуляра на расстоянии меньше его фокусного расстояния. Окончательное изображение 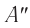(увеличенное мнимое и перевернутое) образуется на сетчатке глаза (см. рис. 95). Увеличение 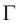, которое дает труба Кеплера:

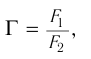
где 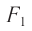— фокусное расстояние объектива,  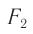— фокусное расстояние окуляра. Длина телескопа .

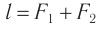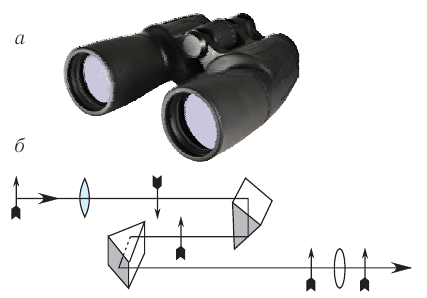
Рис. 96. Бинокль: а — общий вид; б — оборачивающая система призм

Две маленькие подзорные трубы, составленные вместе для двух глаз, образуют бинокль (рис. 96, а). Поскольку труба Кеплера дает перевернутое изображение, то в биноклях, построенных на ее основе, применяется оборачивающая система из двух призм с полным отражением (рис. 96, б).

Наличие двух призм позволяет создать прямое изображение, так как одна призма поворачивает изображение в вертикальной плоскости, другая — в горизонтальной. Кроме того, благодаря призмам объективы в полевом бинокле можно раздвинуть больше, чем окуляры, которые приставляются к глазам (см. рис.96). Соответственно, изображение в таком бинокле не только приближено, но и объемно.

Пример №6

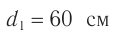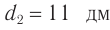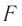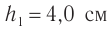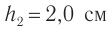Один и тот же предмет фотографируют дважды с расстояний и . Определите фокусное расстояние объектива фотоаппарата, если высота изображений предмета на снимках и соответственно.

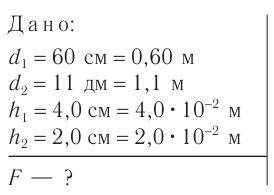
Решение

Линейное увеличение предмета высотой 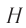в первом и втором случаях соответственно:

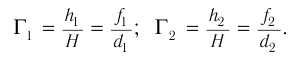
Запишем формулу тонкой линзы для этих случаев:

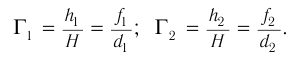
Из первых двух уравнений находим:

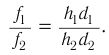
Отсюда

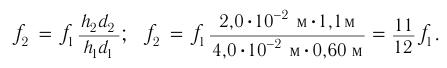
Подставим полученное значение в формулу тонкой линзы и решим систему уравнений:

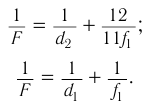
Найдем расстояние:

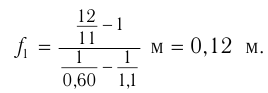
Подставляя полученное значение 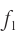, в формулу тонкой линзы, найдем искомое фокусное расстояние объектива:

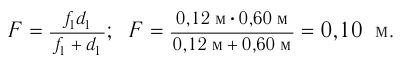
Ответ: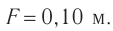

Дисперсия света. Спектр. Спектральные приборы

Источником оптического излучения называется физическое тело, преобразующее любой вид энергии в энергию электромагнитных излучений оптического диапазона. Любой источник света характеризуется полной энергией, которую он излучает в единицу времени. Эта энергия распределяется неравномерно между волнами различной длины. В общем случае произвольный электромагнитный сигнал состоит из набора различных электромагнитных волн, длины (или частоты) которых можно установить.

Подобную процедуру называют спектральным анализом сигнала, а совокупность полученных «простейших» электромагнитных волн — спектром. Таким образом, спектр — распределение энергии, излучаемой или поглощаемой веществом, по частотам или длинам волн.

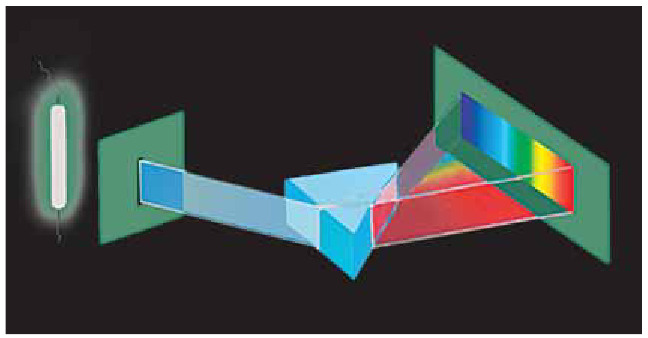
Рис. 97. Разложение белого света призмой

Если направить пучок белого света на призму, то мы обнаружим за призмой на экране разноцветную полоску (рис. 97). Ньютон, впервые проделавший данный эксперимент, назвал ее спектром.

Разложение пучка белого света в спектр призмой является следствием дисперсии (от лат. dispersio — рассеяние) света — зависимости скорости волны в среде от его частоты 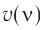. Так как скорость света в веществе 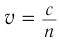,= то абсолютный показатель преломления вещества оказывается зависящим от частоты 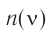или длины волны 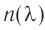распространяющегося излучения. Вследствие явления дисперсии призма различным образом преломляет световые волны разных цветов.

Цвет зависит от частоты световой волны, подобно тому, как различным высотам звука соответствуют различные частоты звуковых волн.

Дисперсия веществ может быть существенно различной. В таблице 6 приведены в качестве примера значения абсолютных показателей преломления некоторых прозрачных веществ.

Дисперсия присуща всем средам, кроме вакуума. Если абсолютный показатель преломления среды уменьшается с ростом длины волны, то такая дисперсия называется нормальной, в противоположном случае — аномальной.

Порядок следования цветов в спектре легко запомнить с помощью известной фразы:

• красный — 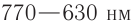    каждый
• оранжевый — 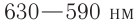    охотник
• желтый — 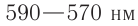    желает
• зеленый — 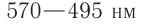    знать,
• голубой, синий — 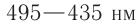    где сидят
• фиолетовый — 435—390 нм    фазаны

Таблица 6. Зависимость абсолютных показателей преломления веществ от длины волны

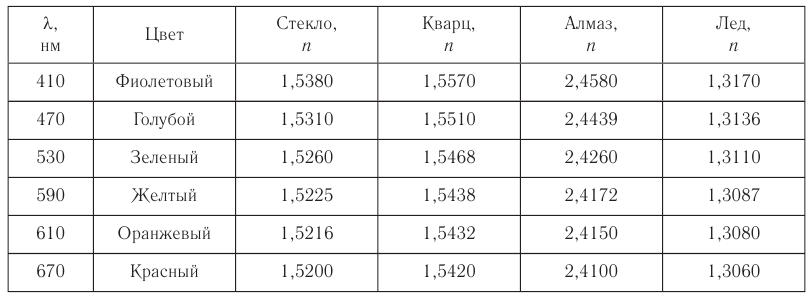
Явления дисперсии и полного отражения приводят к образованию радуги, вследствие преломления солнечных лучей на мельчайших водяных капельках во время дождя, к нежелательному «окрашиванию» изображений в оптических системах (хроматическая аберрация) и т. д.

Измерения и наблюдения оптических спектров производятся с помощью специальных приборов. Приборы для визуального наблюдения спектров называются спектроскопами, приборы с фотографической регистрацией спектров — спектрографами (применяются в различных областях спектра с соответствующей чувствительностью фотоматериалов), приборы с фотоэлектрическими и тепловыми приемниками излучения — спектрометрами или спектрофотометрами (рис. 98).

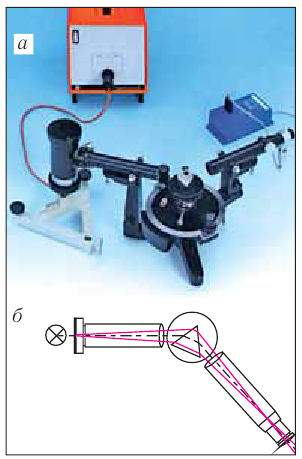
Рис. 98. Призменный спектрофотометр: а — общий вид; б — оптическая схема

Первый спектроскоп сконструировал в 1815 г. немецкий физик Иозеф Фраунгофер.

Любой спектральный прибор имеет входной коллиматор, диспергирующий элемент (призма, дифракционная решетка) и выходной коллиматор.

Входной коллиматор 1 (рис. 99) представляет собой трубу, на одном конце которой имеется ширма с узкой щелью, а на другом — собирающая линза 4. Входная щель, освещенная исследуемым излучением, устанавливается в фокусе собирающей линзы 4, которая образует параллельный пучок света и направляет его на диспергирующий элемент 2.

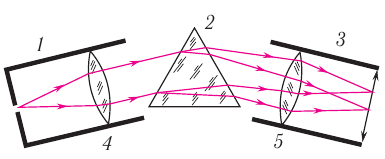
Рис. 99. Устройство спектрографа: 1 — входной коллиматор; 2 — диспергирующий элемент (призма); 3 — выходной коллиматор; 4, 5 — линзы

Диспергирующий элемент преобразует исходный пучок в систему параллельных монохроматических пучков, выходящих из элемента под разными углами, зависящими от длины волны излучения. Собирающая линза 5 выходного коллиматора <3 (см. рис. 99) создает на экране (фотопластинке), расположенном в фокальной плоскости линзы, совокупность монохроматических изображений входной щели. В итоге на экране получается пространственное разложение излучения в спектр.

Назначение спектральных приборов — регистрировать зависимость интенсивности спектральных линий от частоты (длины) волны излучения, т. е. фактически определять, из каких монохроматических волн состоит данное излучение.

Напомним, что в качестве диспергирующих элементов спектральных приборов используются призма или дифракционная решетка, причем в наиболее совершенных спектральных приборах используются именно дифракционные решетки.

Итоги:

Оптика — раздел физики, в котором изучают свойства света, его физическую природу и взаимодействие с веществом.

Под светом понимают электромагнитные волны с частотами от 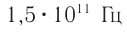до 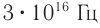 (длины волн изменяются в диапазоне, соответствующем инфракрасному, видимому и ультрафиолетовому излучению).

Электромагнитные волны распространяются в вакууме с максимально возможной в природе скоростью переноса энергии — .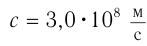

Скорость распространения света в веществе определяется соотношением

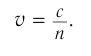
Абсолютный показатель преломления вещества равен отношению модуля скорости света в вакууме к модулю скорости света в веществе:

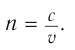
Длина волны 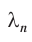 в веществе определяется соотношением:

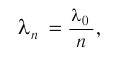
где 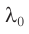— длина волны в вакууме, 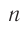— абсолютный показатель преломления вещества.

При переходе световой волны из вакуума в вещество или из одного вещества в другое частота света остается неизменной.

Интерференция света — явление возникновения устойчивой во времени картины чередующихся максимумов и минимумов амплитуд результирующей волны при сложении двух (или нескольких) когерентных волн.

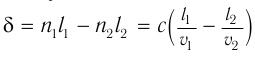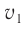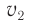Оптическая разность хода волн — разность расстояний, пройденных волнами, с учетом их различных модулей скоростей  и распространения в этих средах с показателями преломления 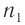и .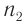

Условие максимумов интерференции:

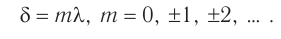
Условие минимумов интерференции:

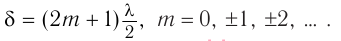
Устойчивое во времени распределение амплитуд колебаний в пространстве при интерференции называется интерференционной картиной.

Принцип Гюйгенса — Френеля: все вторичные источники, расположенные на волновом фронте, когерентны между собой. Огибающая волна, получающаяся в результате интерференции вторичных волн, совпадает с волной, испускаемой источником.

Явление огибания волнами препятствий, которое проявляется в отклонении направления распространения волн от прямолинейного, называется дифракцией.

Дифракционной решеткой называют оптический прибор, предназначенный для разложения света в спектр и точного измерения длин волн. Он состоит из большого числа равноотстоящих параллельных штрихов, нанесенных на стеклянную или металлическую поверхности.

Под лучом понимают линию, вдоль которой переносится энергия электромагнитной волны.

Геометрической оптикой называют раздел оптики, в котором изучаются законы распространения света в прозрачных средах на основе представления о нем как о совокупности световых лучей.

Изменение направления распространения света при прохождении через границу раздела двух сред называется преломлением света.

Закон преломления света:

отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух данных сред и равная относительному показателю преломления второй среды относительно первой;

лучи, падающий и преломленный, лежат в одной плоскости с перпендикуляром, проведенным в точке падения луча к плоскости границы раздела двух сред:

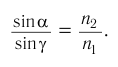
Явление полного отражения падающего луча от границы раздела сред называется полным отражением света. Наименьший угол, с которого начинается полное отражение, называется предельным углом полного отражения:

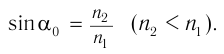
Формула тонкой линзы:

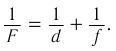
Правило знаков:

в случае собирающей линзы, действительных источника и изображения знаки перед величинами 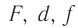следует выбирать положительными; в случае рассеивающей линзы, мнимого источника и изображения знаки выбирают отрицательными.

Линейным (поперечным) увеличением 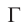называется отношение линейного размера изображения 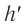к линейному размеру предмета :

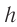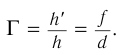
Цифровой фотоаппарат — оптический прибор, предназначенный для получения и записи оптического изображения на электронные носители (флэш-карты, диски и т. д.).

Лупа — оптический прибор (собирающая линза), позволяющий увеличить угол зрения.

Микроскоп — оптический прибор для получения сильно увеличенных изображений объектов или деталей их структуры, не видимых невооруженным взглядом.

Спектр — распределение энергии, излучаемой или поглощаемой веществом, по частотам или длинам волн.

Измерения и наблюдение оптических спектров производятся с помощью спектральных приборов. Назначение спектральных приборов — регистрировать зависимость интенсивности спектральных линий от частоты (длины) волны излучения, т. е. определять, из каких монохроматических волн оно состоит.