Определение усилий в стержнях, поддерживающих плиту в теоретической механике

Определение усилий в стержнях, поддерживающих плиту:

Постановка Задачи. Однородная прямоугольная горизонтальная плита известного веса опирается на шесть невесомых шарнирно закрепленных по концам стержней. Вдоль ребра плиты действует сила. Определить усилия в стержнях.

План решения:

1.    Отделяем плиту от стержней, заменяя действие стержней их реакциями. Реакции направляем вдоль стержней, от плиты. Вес однородной прямоугольной плиты прикладываем к ее центру' вертикально вниз.

2.    Две оси системы координат направляем вдоль сторон плиты, третью — перпендикулярно ее плоскости. Начало координат помещаем в точку, в которой сходится наибольшее число стержней. Составляем уравнения равновесия (три уравнения в проекциях на оси и три уравнения моментов относительно осей). Решаем полученную систему.

3. Выполняем проверку решения, подставляя найденные значения в уравнение моментов относительно какой-либо дополнительной оси.

Задача:

Однородная прямоугольная горизонтальная плита весом G = 20 кН опирается на шесть невесомых шарнирно закрепленных по концам стержней. Вдоль ребра плиты действует сила F = 10 кН (рис. 68). Даны размеры: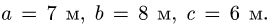

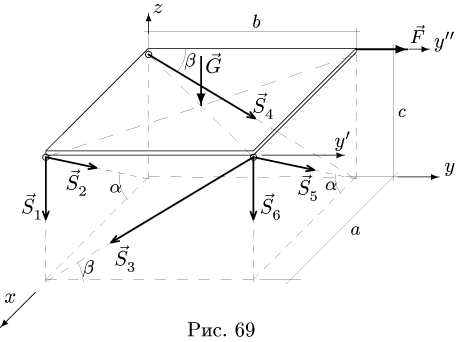
1. Отделяем плиту от стержней, заменяя действие стержней их реакциями. Реакции направляем вдоль стержней, от плиты. Вес однородной прямоугольной плиты прикладываем к ее центру вертикально вниз (рис. 69).

2. Выбираем систему координат (рис. 69) и составляем уравнения равновесия. В уравнение проекций на ось х не входят силы 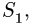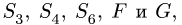лежащие в плоскостях, перпендикулярных Ох. В уравнение проекций на ось у не входят силы 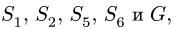лежащие в плоскостях, перпендикулярных Оу, а в уравнение проекций на вертикальную ось 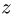входят все силы, кроме горизонтальной F:

4.4.Определение усилий  в стержнях ,поддерживающих плиту

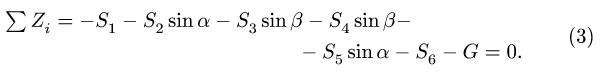
Линии действия сил 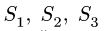пересекают ось x, поэтому их моменты относительно этой оси равны нулю. Вычисляя момент силы 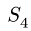относительно оси х, разложим ее на горизонтальную составляющую 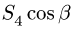плечом с относительно х и вертикальную — 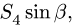которая пересекает ось и имеет момент равный нулю.

Аналогично вычисляем моменты других сил и записываем все три уравнения моментов:

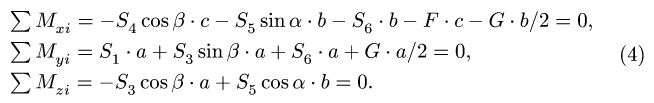
Находим необходимые значения тригонометрических функций:

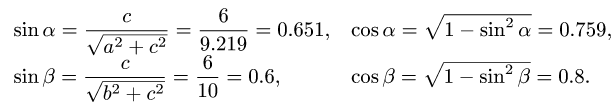
Решая систему шести уравнений (1-4) с шестью неизвестными, получаем значения усилий, которые заносим в таблицу (в кН):

3. Выполняем проверку решения, подставляя найденные значения в уравнение моментов относительно дополнительной оси 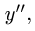проведенной в плоскости плиты параллельно у:

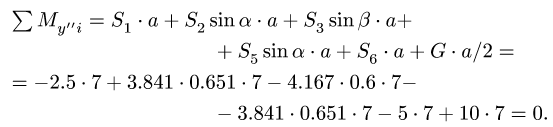
Замечание. Некоторые (или все) уравнения проекций можно заменить на уравнения моментов относительно других осей. Например, в нашей задаче вместо сложного уравнения 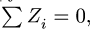 в которое входят все неизвестные усилия, удобно использовать более простое уравнение моментов относительно оси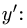

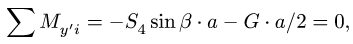
из которого сразу же находится усилие

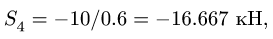
а уравнение 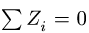можно использовать как проверочное, тем более, что выполнение такой проверки означает правильность сразу всех найденных усилий.