
Определение траектории, скорости и ускорения точки в теоретической механике
Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме:
Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат.
Движение точки в пространстве задается тремя уравнениями:

Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).
Если закон движения точки задан в координатной форме, то:
а) траектория плоского движения точки выражается уравнением
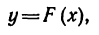
которое образуется из данных уравнений движения после исключения времени t
б) числовое значение скорости точки находится из формулы
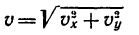
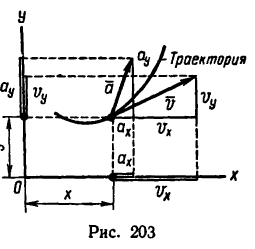
после предварительного определения проекции (см. рис. 203) скорости на оси координат
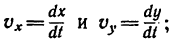
в) числовое значение ускорения находится из формулы
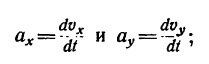
после предварительного определения проекций координат
г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.
Задача:
Движение точки А задано уравнениями:
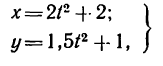
где  Определить траекторию движения точки, скорость и ускорение в моменты
Определить траекторию движения точки, скорость и ускорение в моменты 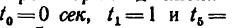
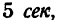 а также путь пройденный точкой за 5 сек.
а также путь пройденный точкой за 5 сек.
Решение.
I. Определяем траекторию точки. Умножаем первое заданное уравнение на 3, второе — на ( — 4), а затем складываем их левые
и правые части:
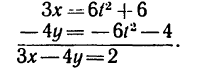
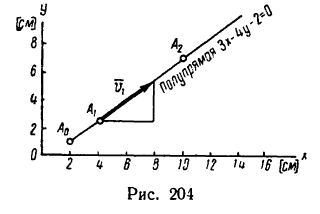
Получилось уравнение первой степени— уравнение прямой линии, значит движение точки — прямолинейное.
Для того чтобы определить координаты  — начального положения точки, подставим в данные уравнения значение
— начального положения точки, подставим в данные уравнения значение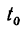 = 0; из первого уравнения получим
= 0; из первого уравнения получим 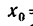 = 2 см, а из второго
= 2 см, а из второго 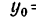 =1 см (рис. 204). Замечая, что при любом другом значении t (так как в оба уравнения t входит во второй степени) координаты х и у движущейся точки только возрастают, делаем окончательный вывод: траекторией точки служит полупрямая
=1 см (рис. 204). Замечая, что при любом другом значении t (так как в оба уравнения t входит во второй степени) координаты х и у движущейся точки только возрастают, делаем окончательный вывод: траекторией точки служит полупрямая
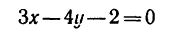
с началом в точке 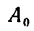 (2; 1).
(2; 1).
2. Определяем скорость движения точки, для чего сначала найдем ее проекции на оси координат:
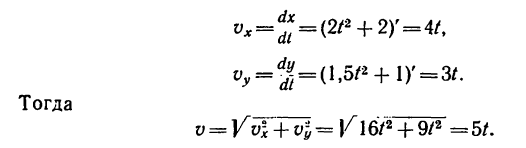
Таким образом, уравнение скорости имеет вид
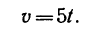
При 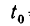 = 0 начальная скорость точки
= 0 начальная скорость точки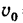 = 0
= 0
При 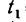 = 1 сек скорость точки
= 1 сек скорость точки 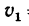 =5 см сек.
=5 см сек.
При 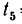 = 5 сек скорость точки
= 5 сек скорость точки 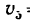 = 25 см'сек.
= 25 см'сек.
3. Определяем ускорение точки.
Проекции ускорения на оси координат: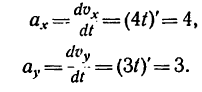
Как видно, проекции ускорения не зависят от времени движения, значит ускорение тоже постоянно и
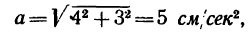
т. е. движение точки равноускоренное.
4. Так как в данном случае движение точки прямолинейное, то модуль ускорения можно определить путем непосредственного дифференцирования уравнения скорости:
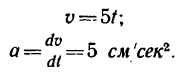
5. Как установлено, движение точки прямолинейное, равноускоренное, значит векторы скорости и ускорения совпадают с траекторией точки, т. е. направлены вдоль полупрямой Зx— 4у—2 = 0. На рис. 204 показан вектор скорости 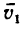 (скорость точки в момент
(скорость точки в момент 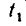 = 1 сек).
= 1 сек).
6. Определяем путь, пройденный точкой за первые 5 сек движения. Выразим предварительно путь как функцию времени t.Зная, что 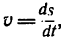 имеем
имеем
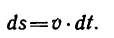
Проинтегрируем последнее выражение)
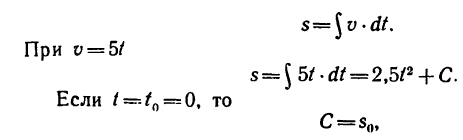
но так как в данном случае начальное расстояние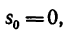 то окончательно
то окончательно
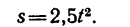
И теперь находим, что за t = 5 сек точка проходит расстояние 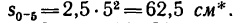
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Кинематический способ определения радиуса кривизны траектории
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Равномерное прямолинейное движение точки
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории